Category: CBSE Class 7

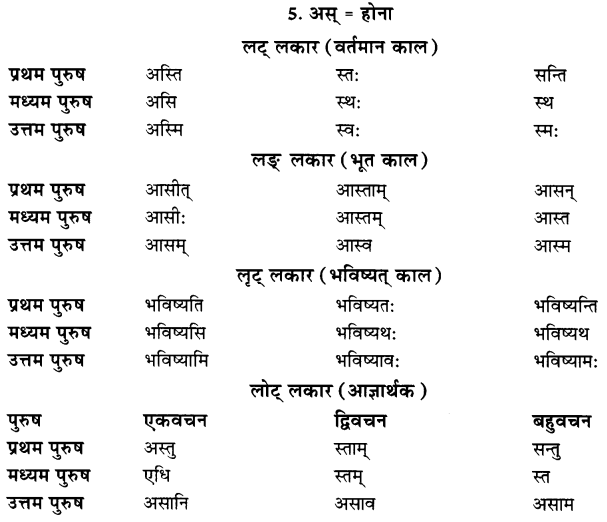
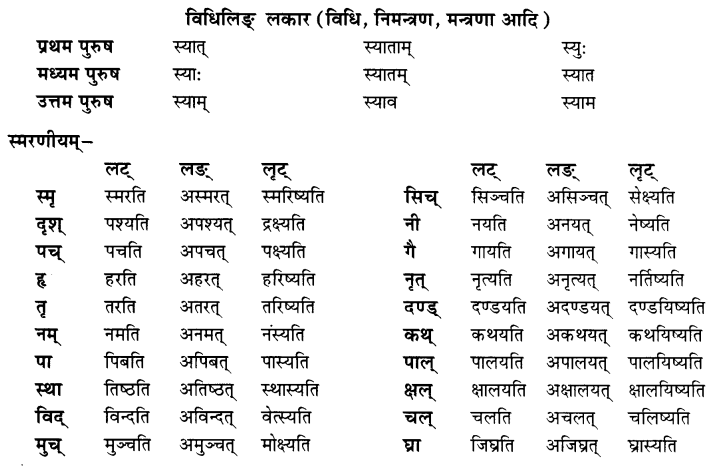
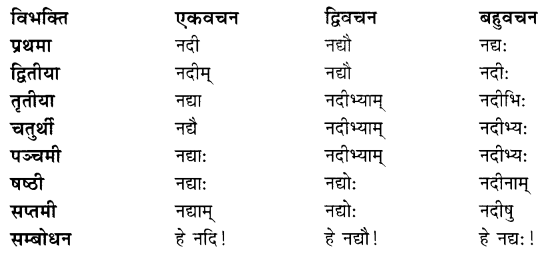
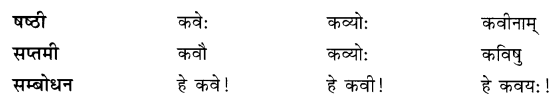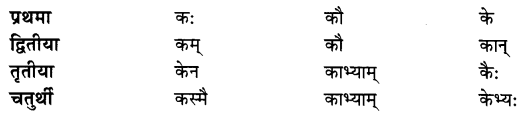We have given detailed NCERT Solutions for Class 7 Sanskrit Ruchira Chapter 7 सड.कल्पः सिद्धिदायकः Questions and Answers come in handy for quickly completing your homework.

NCERT Solutions for Class 7 Sanskrit Ruchira Chapter 7 सड.कल्पः सिद्धिदायकः

Class 7 Sanskrit Chapter 7 सड.कल्पः सिद्धिदायकः Textbook Questions and Answers

प्रश्न: 1.
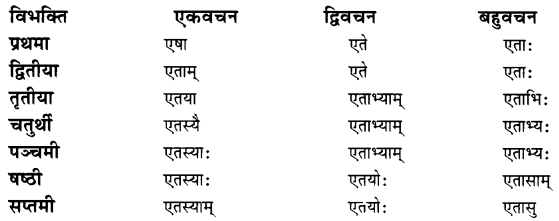
उच्चारणं कुरुत- (उच्चारण कीजिए- Pronounce these.)

उत्तराणि:
छात्र ध्यानपूर्वक उच्चारण करें।

प्रश्न: 2.
उदाहरणम् अनुसृत्य रिक्तस्थानानि पूरयत- (उदाहरण के अनुसार रिक्त स्थानों की पूर्ति कीजिए Fill in the blanks according to the examples.)


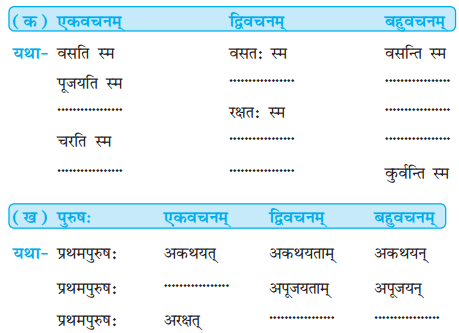
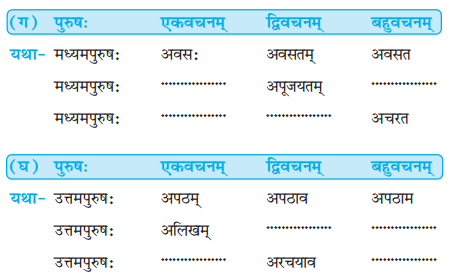
उत्तराणि:

प्रश्न: 3.
प्रश्नानाम् उत्तराणि एकपदेन लिखत- (प्रश्नों के उत्तर एक शब्द में लिखिए- Write answers of the questions in one word.)

(क) तपःप्रभावात् के सखायः जाता:?
उत्तराणि:
हिंस्रपशवः

(ख) पार्वती तपस्यार्थं कुत्र अगच्छत् ?
उत्तराणि:
गौरीशिखरम्

(ग) कः श्मशाने वसति?
उत्तराणि:
शिवः

(घ) शिवनिन्दां श्रुत्वा का क्रुद्धा जाता?
उत्तराणि:
पार्वती

(ङ) वटुरूपेण तपोवनं कः प्राविशत् ?
उत्तराणि:
शिवः ।

प्रश्न: 4.
कः/का कम्/काम् प्रति कथयति। [कौन (पुल्लिग/स्त्रीलिंग) किसको (पुल्लिग/स्त्रीलिंग) कहता है।] (Who said the following sentences to whom.)

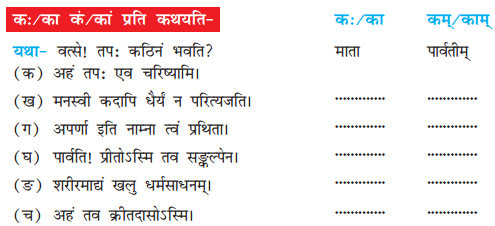
उत्तराणि:

प्रश्न: 5.
प्रश्नानाम् उत्तराणि लिखत । (प्रश्नों के उत्तर लिखिए। Answer the following questions.)

(क) पार्वती क्रुद्धा सती किम् अवदत्?
उत्तराणि:
पार्वती क्रुद्धा सती अवदत्-‘अरे वाचाल! अपसर। जगति न कोऽपि शिवस्य यथार्थं स्वरूपं जानाति।’

(ख) कः पापभाग् भवति?
उत्तराणि:
यः शिवस्य निन्दा करोति यः च शृणोति, सः पापभाग् भवति।

(ग) पार्वती किं कर्तुम् ऐच्छत्?
उत्तराणि:
पार्वती तपः कर्तुम् ऐच्छत्।

(घ) पार्वती कया साकं गौरीशिखरं गच्छति?
उत्तराणि:
पार्वती स्वसख्या विजयया साकं गौरी शिखरं गच्छति।

प्रश्न: 6.
मञ्जूषातः पदानि चित्वा समानार्थकानि पदानि लिखत- (मञ्जूषा से शब्दों को चुनकर समान अर्थ वाले शब्द लिखिए– Write synonyms choosing from the box.)

माता, मौनम्, प्रस्तरे, जन्तवः, नययानि

1. शिलायां – ………………
2. पशवः – ………………
3. अम्बा – ………………
4. नेत्राणि – ………………
5. तूष्णीम् – ………………
उत्तरम् –
1. प्रस्तरे
2. जन्तवः
3. माता
4. नयनानि
5. मौनम्।

प्रश्नः 7.
उदाहरणानुसारं पदरचनां कुरुत। (उदाहरण के अनुसार शब्द-रचना कीजिए। Make words ac cording to the example.)

(अ) यथा-वसति स्म = अवसत्

(क) पश्यति स्म = …….
(ख) तपति स्म = …………
(ग) चिन्तयति स्म = …..
(घ) वदति स्म = …..
(ङ) गच्छति स्म = …..
उत्तराणि:
(अ) (क) अपश्यत्
(ख) अतपत्
(ग) अचिन्तयत्
(घ) अवदत्
(ङ) अगच्छत्

(ब) यथा-अलिखत् = लिखति स्म
(क) ………………… = कथयति स्म
(ख)…………………….. = नयति स्म
(ग) ……………..= पठति स्म
(घ) ……………………. = धावति स्म
(ङ) ………………… = हसति स्म
उत्तराणि:
(ब) (क) अकथयत्
(ख) अनयत्
(ग) अपठत्
(घ) अधावत्
(ङ) अहसत्

Class 7 Sanskrit Chapter 7 सड.कल्पः सिद्धिदायकः Additional Important Questions and Answers

(1) एकपदेन उत्तरत- (एक पद में उत्तर दीजिए- Answer in a word.)

(i) पार्वती शिवं केन रूपेण ऐच्छत्?
उत्तराणि:
पतिरूपेण

(ii) मनस्वी किं न त्यजति?
उत्तराणि:
धैर्यम्

(iii) शिवः केन रूपेण आश्रमे आगच्छत्?
उत्तराणि:
वटुरूपेण

(iv) कस्य प्रभावात् हिंस्रपशवः पार्वत्याः सखायः जाताः?
उत्तराणि:
तपसः (तपः प्रभावात्)

(v) शिवः पार्वत्याः केन प्रीत:/प्रसन्न?
उत्तराणि:
सङ्कल्पेन/दृढ़सङ्कल्पेन

(vi) पार्वती कया सह गौरीशिखरं गच्छति स्म?
उत्तराणि:
विजयया

(vii) का पार्वती तपश्चरणात् निवारयति स्म?
उत्तराणि:
माता मेना

(2) पूर्णवाक्येन उत्तरत- (पूरे वाक्य में उत्तर दीजिए- Answer in complete sentence.)

(i) पार्वती सङ्कल्पसिद्धये किम् अकरोत्?
उत्तराणि:
सङ्कल्पसिद्धये पार्वती कठिनं तपः अकरोत्।

(ii) माता मेना कथं चिन्तिता आसीत्?
उत्तराणि:
माता मेना चिन्तिता आसीत् यतः हि तपः कठिनं पार्वत्याः शरीरं च कोमलम् अस्ति।

(iii) क : पापभाग् भवति?
उत्तराणि:
यः निन्दां करोति सः पापभाग् भवति यः च निन्दांशृणोति सः अपि पापभाग् भवति।

(3) पाठांशं पठत अधोदत्तान् प्रश्नान् च उत्तरत- (पाठांश पढ़िए और नीचे दिए गए प्रश्नों के उत्तर दीजिए- Read the extract and answer the questions that follow.)

मेना- वत्से! मनीषिता देवताः गृहे सन्ति। तपः कठिनं भवति। तव शरीरं सुकोमलं वर्तते। गृहे एव वस। अत्रैव तवाभिलाषः सफलः भविष्यति।
पार्वती- अम्ब! तादृशः अभिलाषः तु तपसा एव पूर्णः भविष्यति। अन्यथा तादृशं च पतिं कथं प्राप्स्यामि। अहं तपः एव चरिष्यामि इति मम सङ्कल्पः।

I. एकपदेन उत्तरत-(एक पद में उत्तर दीजिए-Answer in a word.)

1. मनीषिता देवाः कुत्र वसन्ति?
उत्तराणि:
गृहे

2. पार्वत्याः कः सफलः भविष्यति?
उत्तराणि:
अभिलाषः

II. पूर्णवाक्येन उत्तरत- (पूर्ण वाक्य में उत्तर दीजिए- Answer in complete sentence.)

पार्वत्याः अभिलाषः कः? तदर्थं सा किं करोति?
उत्तराणि:
पार्वती शिवं पतिरूपेण अभिलषति तदर्थं च सा तपः चरति।

III. भाषिक कार्यम् –

यथानिर्देशम् उत्तरत (निर्देशानुसार उत्तर दीजिए- Answer as directed.)

(i) ‘तव शरीरं सुकोमलम्’- अत्र विशेषणपदम् किम्?
उत्तराणि:
सुकोमलम्

(ii) ‘मनोरथः’ इति पदस्य पर्यायम् चित्वा लिखत –
उत्तराणि:
अभिलाषः

(iii) ‘मनीषिताः देवाः गृहे एव वसन्ति’ –
अस्मिन् वाक्ये ‘वसन्ति’ क्रियापदस्य कर्ता कोऽस्ति? (मनीषिताः, गृहे, देवाः)
उत्तराणि:
देवाः

(iv) ‘गृहे’ अत्र किम् विभक्तिवचनम्? (प्रथमा द्विवचनम्, द्वितीया द्विवचनम्, सप्तमी एकवचनम्)
उत्तराणि:
सप्तमी एकवचनम्

(v) पाठांशात् एकम् अव्ययपदं चित्वा लिखत।
उत्तराणि:
‘एव’ अथवा ‘अन्यथा’

(4) परस्परमेलनम् कुरुत- (परस्पर मेल कीजिए- Match the following.) 

तूष्णीम् – सह
सखायः- इष्टाः
मनीषिताः – वस्त्रम्
वसनम् – मित्राणि
साकम् – मौनम्
उत्तराणि:
तूष्णीम् – मौनम्
सखायः- मित्राणि
मनीषिताः – इष्टाः
वसनम् – वस्त्रम्
साकम् – सह

(5) अधोदत्तानि वाक्यानि घटनाक्रमेण योजयत। (निम्नलिखित वाक्यों को घटना के क्रम में लगाइए। Arrange the following sentences in the order of events in the story.)

(i) पार्वती वटोः मुखात् शिवनिन्दा श्रुत्वा क्रुद्धा जाता।
उत्तराणि:
पार्वती शिवं पतिरूपेण अवाञ्छत्।

(ii) परं पार्वती दृढ़संकल्पा आसीत्।
उत्तराणि:
एतदर्थं सा कठोरां तपस्यां कर्तुम् ऐच्छत्।

(iii) एतदर्थं सा कठोरां तपस्या कर्तुम् ऐच्छत्।
उत्तराणि:
एतत् श्रुत्वा तस्याः माता अति चिन्तिता आसीत्।

(iv) सा सख्या विजयया सह वने अगच्छत्।
उत्तराणि:
परं पार्वती दृढ़संकल्पा आसीत्।

(v) पार्वती शिवं पतिरूपेण अवाञ्छत्।
उत्तराणि:
सा सख्या विजयया सह वने अगच्छत्।

(vi) तस्याः दृढ़-संकल्पेन शिवः अतीव प्रसन्नः अभवत्।
उत्तराणि:
एकदा शिवः वटुरूपेण तत्र आगच्छत्।

(vii) एतत् श्रुत्वा तस्याः माता अति चिन्तिता आसीत्।
उत्तराणि:
पार्वती वटोः मुखात् शिवनिन्दां श्रुत्वा क्रुद्धा जाता।

(viii) एकदा शिवः वटुरूपेण तत्र आगच्छत्।
उत्तराणि:
तस्याः दृढ़-संकल्पेन शिवः अतीव प्रसन्नः अभवत्।

(1) उचितं विकल्पं प्रयुज्य प्रश्ननिमार्णं कुरुत- (उचित विकल्प का प्रयोग करके प्रश्ननिर्माण
alloty- Frame questions by using the correct option.)

(i) पार्वती तपः चरितुं वने अगच्छत्। (कः, किम्, कथम्)
उत्तराणि:
पार्वती किम् चरितुम् वने अगच्छत्?

(ii) सा रात्रौ शिलायां स्वपिति स्म। (कस्याम्, काम्, किम्)
उत्तराणि:
सा रात्रौ कस्याम् स्वपिति स्म?

(iii) तपः प्रभावात् हिंस्रपशवः अपि तस्याः सखायः जाताः। (काः, के, कः)
उत्तराणि:
तपः प्रभावात् के अपि तस्याः सखायः जाताः?

(iv) मनोरथानाम् अगतिः नास्ति। (काम्, कस्य, केषाम्)
उत्तराणि:
केषाम् अगतिः नास्ति?

(v) शिवस्य निन्दां श्रुत्वा पार्वती क्रुद्धा जाता। (काम्, कस्य, किम्)
उत्तराणि:
कस्य निन्दां श्रुत्वा पार्वती क्रुद्धा जाता?

(vi) तपः कठिनम् भवति। (कीदृशः, कीदृशम्, कीदृशी)
उत्तराणि:
तपः कीदृशं भवति?

(2) प्रदत्तविकल्पेभ्यः उचितं पदं चित्वा वाक्यपूर्तिं कुरुत- (दिए गए विकल्पों में से उचित पद चुनकर वाक्यपूर्ति कीजिए- Pick out the appropriate word form the options given and complete the sentences.)

(क) (i) अद्यैव साकं गौरीशिखरं गमिष्यामि। (विजया, विजयेन, विजयया)
उत्तराणि:
विजयया

(i) अपि .. ! त्वं सत्यमेव शिवं पतिम् इच्छसि? (पार्वती, पार्वति, पार्वतिः)
उत्तराणि:
पार्वति

(ii) यः ……. करोति सः तु पापभाग्।(निन्दा, निन्दाम्, निन्दम्)
उत्तराणि:
निन्दाम्

(iv) .. रूपं परित्यज्य शिवः तस्याः हस्तं गृह्णाति। (वटुस्य, वटोः, वटुः)
उत्तराणि:
वटोः

(v) इयं मे ….पार्वती। (सखि, सखीः, सखी)
उत्तराणि:
सखी

(vi) अयि ” किं न जानासि? (विजये, विजया, विजयि)
उत्तराणि:
विजये।

(ख) (i) त्वं पञ्चाग्नि-व्रतम् अपि । (अतपत्, अतपति, अतपः)
उत्तराणि:
अतपः

(ii) पार्वती शिवं पतिं ……। (इच्छति, इच्छसि, इच्छति स्म)
उत्तराणि:
इच्छति स्म

(iii) अहं तव तपोभिः क्रीतदासः .. (अस्ति, असि, अस्मि)
उत्तराणि:
अस्मि

(iv) अयि भोः! अहम् तृषार्तः जलम् . . (वाञ्छति, वाञ्छामि, वाञ्छसि)
उत्तराणि:
वाञ्छामि

(v) पूज्याः पितृचरणाः गृहे एव । (अस्ति, सन्ति, स्तः)
उत्तराणि:
सन्ति

(vi) ” ” भवान्। (उपविशसि, उपविशतु, उपविशति)
उत्तराणि:
उपविशतु।

(ग) (i) सर्वे सानन्दम् भोजनम् …… । (अखादत्, अखादत, अखादन्)
उत्तराणि:
अखादन्

(ii) किं पितामहः भ्रमणाय …………… । (गच्छन्ति, अगच्छन्, गच्छति स्म)
उत्तराणि:
गच्छति स्म

(iii) गतवर्षे वयम् मुम्बईनगरे (अवसामः, वसामः, अवसाम)
उत्तराणि:
अवसाम

(iv) तस्मिन् वृक्षे चटकाः …………. । (निवसन्ति स्म, निवसति, निवसति स्म)
उत्तराणि:
निवसन्ति स्म

(v) किं त्वं सावधानो भूत्वा पाठम् .। (अपठत्, अपठः, अपठसि)
उत्तराणि:
अपठः

We have given detailed NCERT Solutions for Class 7 Sanskrit Grammar Book धातुरूपाणि Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 7 Solutions धातुरूपाणि

अधोदत्तानि वाक्यानि अवलोकयत।
(नीचे दिए गए वाक्यों को देखिए। Look at the setences given gelow.)
1. अद्य सुदीपः विज्ञान-विषयं पठति।
(आज सुदीप विज्ञान विषय पढ़ रहा है। Today Sudeep is reading the subject of science.)

2. ह्यः सः गणितविषयम् अपठत्।
(कल उसने गणित विषय पढ़ा। Yesterday he studied the subject of Mathematics.)

3. श्वः सः संस्कृतम् पठिष्यति।
(वह कल संस्कृत पढ़ेगा। Tomorrow he will study Sanskrit.)

4. पुत्र, ध्यानेन पठ।
(पुत्र ध्यान से पढ़ो। Son, read carefully.)

5. यथाकालं पठेत् यथाकालं च क्रीडेत्।
(उचित समय पर पढ़ना चाहिए और उचित समय पर खेलना चाहिए। One should study at the right time and play at the right time.)

उपरिलिखित वाक्यों में स्थूल अक्षरों में आए शब्द- पठति, अपठत्, पठिष्यति, पठ, पठेत्-क्रियापद हैं। ये सब क्रियापद पठ् धातु से बने हैं। क्रिया का बोध कराने वाले पद क्रियापद कहलाते हैं। सभी क्रियापद धातुओं से बनते हैं। प्रत्येक धातु के रूप पाँच लकारों’ में चलते हैं। काल
तथा अवस्था दर्शाने के लिए विविध लकारों का प्रयोग होता है।

1. लट्लकारः – (वर्तमान काल, Present Tense) – पठति (पढ़ता / पढ़ती है, reads)
2. लङ्ल कारः – (भूतकाल, Past Tense) – अपठत् (पढ़ा / पढ़ी, read)
3. लुट्लकार: – (भविष्यत् काल, Future Tense) – पठिष्यति (पढ़ेगा / पढ़ेगी है, will read)
4. लोट्लकार: – (आज्ञार्थक, Imperative Mood) – पठ (पढ़ो, read)
5. विधिलिङ्लकार: – (विध्यर्थक, Potential Mood) – पठेत् (पढ़ना चाहिए)

(In the sentences given above, words in bold letters- पठति, अपठत्, पठिष्यति, पठ, पठेत् are Verbs. All these are formed from the root 46. Verbs are words that tell us about an action. All verbs are formed from roots. Each root is conjugated in 5 लकार. which are used to denote either time or Mood of Action as is clear from the above.)

पिछली कक्षा में हमने सीखा लट् लकार का प्रयोग वर्तमान काल तथा लृट् लकार का प्रयोग भविष्यत् काल की क्रिया को दर्शाने के लिए होता है। आवृत्ति हेतु नीचे ‘पठ्’ के ‘लट्’ व ‘लुट’ में रूप दिए गए हैं। (We learnt in the last class that लट् लकार is used to denote action in the present tense and is not is used for future tense. Given below is the conjugation of the root ‘पठ्’ in ‘लट’ and ‘लुट’ for the sake of revision.)

लङ्लकारः
भूतकाल – Past Tense
लङ् लकार का प्रयोग भूतकाल की क्रिया को दर्शाने के लिए किया जाता है। नीचे दिए गए ‘पठ्’ धातु के रूप व प्रयोग को देखिए। (लङ् लकार is used to denote action in the past tense. Look at the conjugation of the root ‘8’ and its usage given below.)

पठ्-लङ्लकारः

वाक्य-प्रयोगः
(क) सः बालक: / सा बालिका अपठत्।
किम् त्वम् अपठः?
अहम् न अपठम्।

(ख) तौ बालको / ते बालिके अपठताम्।
किम् युवाम् अपठतम्?
आवाम् अपि अपठाव।

(ग) ते बालकाः / ताः बालिकाः अपठन्।
किम् यूयम् अपठत?
आम्, वयम् अपठाम।

अभ्यासः

प्रश्न 1.
तालिकापूर्ति कुरुत- (तालिकापूर्ति कीजिए- Complete the tables.)

उत्तरम्-

प्रश्न 2.
‘क’ खण्डस्य वाक्यानि कोष्ठके दत्तस्य धातोः लट्लकाररूपैः ‘ख’ खण्डस्य च लृट्लकार रूपैः पूरयत-
[(‘क’ खण्ड के वाक्य कोष्ठक में दी गई धातु के लट् लकार के रूप से तथा ‘ख’ खण्ड के लृट् लकार के रूप से पूरे कीजिए- Complete the sentences of section ‘क’ by using लट् लकार (Present tense) and those of section ‘ख’ with लृट् लकार (Future tense) form of the root in bracket.)]
(क) 1. तौ छात्रौ पाठम् ______________ (स्मृ)।
2. आवाम् भोजनम् ______________ (खाद्)।
3. युवाम् किम् ______________ (कृ)?
4. वयम् वीराः सैनिकाः ______________ (अस्)।
5. ते अधुना कार्टून-चित्रम् ______________ (दृश्)।
6. सुनीलः मित्राय उपहारम् ______________ (दा)।
7. किम् त्वम् दुग्धम् न ______________ (पा)?
8. सा पुष्पाणि ______________ (घ्रा/जिघ्र)।
9. शेखरः मोदकान् ______________ [गण (गणय्)]।
उत्तरम्-
1. स्मरतः
2. खादावः
3. कुरुथः
4. स्मः
5. पश्यन्ति
6. यच्छति
7. पिबसि
8. जिघ्रति
9. गणयति

(ख) 1. अम्बा भोजनम् ______________ (पच्)।
2. आवाम् दूरदर्शने क्रिकेट प्रतियोगिताम् ______________ (दृश्)।
3. सा गीतम् ______________ (गै)।
4. वयम् अध्यापकान् ______________ (नम्)।
5. त्वम् गणित-कार्यम् कदा ______________ (कृ)?
उत्तरम्-
1. पक्ष्यति
2. द्रक्ष्याव:
3. गास्यति
4. नस्यामः
5. करिष्यसि

प्रश्न 3.
उदाहरणानुसारं क्रियापदानि रिक्तस्थानेषु लिखत-
(उदाहरणानुसार क्रियापद रिक्त स्थान में लिखिए- Write the verbs in blanks as per example.)
उदाहरणम्- सः चित्रम् अपश्यत्। तौ चित्रम् अपश्यताम्।
1. अहम् मेलकम् अगच्छम्।
किं त्वम् न ______________?

2. वयम् लेखम् अलिखाम।
अहम् लेखम् ______________।

3. सः निबन्धम् अलिखत्?
ते निबन्धम् ______________।

4. तौ श्लोकम् अपठताम्।
किं युवाम् अपि ______________?

5. सा उद्यानम् अगच्छत्।
किं यूयम् न ______________?

6. तौ न अखेलताम्।
किं युवाम् ______________?
उत्तरम्-
1. अगच्छः
2. अलिखम्
3. अलिखन्
4. अपठतम्
5. अगच्छत\
6. अखेलतम्

प्रश्न 4.
निर्देशानुसारं लकारं परिवर्त्य वाक्यानि पुनः लिखत-
(निर्देशानुसार लकार बदलकर वाक्य पुनः लिखिए- Rewrite the sentences after making due changes in tense as per instructions.)
1. अहम् प्रतिदिनं खेलामि। (लङ्)
_____ _____ _____
2. त्वम् उद्याने भ्रमसि। (लृट् )
_____ _____ _____
3. आवाम् विद्यालयम् गच्छावः। (लङ्)
_____ _____ _____
4. युवाम् किं लिखथः? (लुट)
_____ _____ _____
5. तौ गुरून् नस्यतः। (लट्)
_____ _____ _____
6. ते खेलम् अपश्यन्। (लट् )
_____ _____ _____
उत्तरम्-
1. अहं प्रतिदिनम् अखेलम्।
2. त्वम् उद्याने भ्रमिष्यसि।
3. आवाम् विद्यालयम् अगच्छाव।
4. युवाम् किं लेखिष्यथ:?
5. तो गुरून् नमतः।
6. ते खेलम् पश्यन्ति।

प्रश्न 5.
लिख् धातुं लङ्लकारे प्रयोज्य वाक्यपूर्तिं कुरुत-
(लिख् धातु का लङ् लकार में प्रयोग करके वाक्य पूर्ति कीजिए- Fill in the blanks using the root लिख in लङ्ल कार Past Tense.) (क) रोहणः पत्रम् अलिखत्।
त्वम् निबन्धम् ______________।
अहम् सुलेखम् ______________।
(ख) रोहण: रोहितः च किम् ______________?
किं युवाम् अनुच्छेदम् ______________?
नहि, आवाम् निबन्धम् ______________।
(ग) ते स्वच्छम् ______________।
यूयम् अपि स्वच्छम् ______________।
वयम् शीघ्रम् ______________।
उत्तरम्-
(क) अलिखः, अलिखम्।
(ख) अलिखताम्, अलिखतम्, अलिखाव।
(ग) अलिखन्, अलिखत अलिखाम।

We have given detailed NCERT Solutions for Class 7 Sanskrit Grammar Book शब्दरूपाणि Questions and Answers come in handy for quickly completing your homework.

Sanskrit Vyakaran Class 7 Solutions शब्दरूपाणि

संस्कृत व्याकरण में शब्दरूप की दृष्टि से शब्दों को अकारान्त, आकारान्त, इकारान्त, ईकारान्त, उकारान्त, ऋकारान्त वर्गों में बाँटा गया है। शब्द का रूप इस बात पर भी निर्भर करता है कि अमुक शब्द पुल्लिग है, स्त्रीलिंग अथवा नपुंसकलिंग है। सर्वनाम शब्दों के रूप तीनों लिंगों में चलते हैं।
यहाँ प्रत्येक वर्ग के शब्द का उदाहरण दिया जा रहा है। छात्र इन्हें ध्यानपूर्वक पढ़ें तथा समझें।

अकारान्त-पुंल्लिङ्ग-शब्दः
1. नर

एवमेव- बालक-राम-नृप-जनक-देव-छात्र-इत्यादीनाम् अकारान्त पुंल्लिङ्ग-शब्दानां रूपाणि भवन्ति । (इसी प्रकार राम, नृप, बालक, जनक, देव, छात्र इत्यादि अकारान्त पुल्लिंग शब्दों के रूप होते हैं।)
नियम : र्, ऋ तथा ष् के बाद ‘न्’ का ‘ण’ हो जाता है; जैसे- नरेण, नराणाम्। किन्तु अन्त में ‘न्’ नहीं बदलता है। यथा नरान्, वृक्षान् आदि।

इकारान्त पुंल्लिङ्ग-शब्दः
2. कवि

एवमेव- मुनि-हरि-कपि-रवि-इत्यादीनाम् इकारान्त पुंल्लिङ्ग-शब्दानां रूपाणि भवन्ति । (इसी प्रकार मुनि, हरि, कपि, रवि इत्यादि इकारान्त-पुल्लिग शब्दों के रूप होते हैं।)

उकारान्त-पुंल्लिङ्ग-शब्दः
3. साधु

एवमेव- गुरु-भानु-शिशु-प्रभु-विष्णु इत्यादीनाम् उकारान्त पुंल्लिङ्ग-शब्दानां रूपाणि भवन्ति। (इसी प्रकार गुरु, भानु, शिशु, प्रभु, विष्णु इत्यादि उकारान्त-पुल्लिग शब्दों के रूप होते हैं।)

ऋकारान्त-पुंल्लिङ्ग-शब्दः
4. पितृ (पिता)

एवमेव- भ्रातृ-कर्तृ-दातृ-नेतृ-इत्यादीनाम् ऋकारान्त पुंल्लिङ्ग शब्दानां रूपाणि भवन्ति। (इसी प्रकार भ्रातृ, कर्तृ-दातृ-नेतृ इत्यादि ऋकारान्त-पुल्लिग शब्दों के रूप होते हैं।)

आकारान्त-स्त्रीलिङ्ग-शब्दः
5. लता

एवमेव- रमा-कन्या-कक्षा-छात्रा-बालिका-इत्यादीनाम् आकारान्त स्त्रीलिङ्ग-शब्दानां रूपाणि भवन्ति। (इसी प्रकार रमा, कन्या, कक्षा, छात्रा, बालिका इत्यादि आकारान्त स्त्रीलिंग शब्दों के रूप होते हैं।)

ईकारान्त-स्त्रीलिङ्ग-शब्दः
6. नदी

एवमेव- नारी-जननी-भगिनी-पुत्री-इत्यादीनाम् ईकारान्त-स्त्रीलिङ्ग शब्दानां रूपाणि भवन्ति। (इसी प्रकार नारी, जननी, भगिनी, पुत्री इत्यादि ईकारान्त-स्त्रीलिंग शब्दों के रूप होते हैं।)

अकारान्त-नपुंसकलिङ्ग-शब्दः
7. फल

एवमेव- मित्र-पत्र-पुष्प-पुस्तक-नगर-उद्यान-इत्यादीनां अकारान्त नपुंसकलिङ्ग-शब्दानां रूपाणि भवन्ति । (इसी प्रकार मित्र-पत्र-पुष्प-पुस्तक-नगर-उद्यान इत्यादि अकारान्त-नपुंसकलिंग शब्दों के रूप होते हैं।)

सर्वनाम शब्दः
8. एतत् (यह ), पुंल्लिङ्ग

सर्वनाम शब्द रूपों में संबोधन नहीं होता है।

9. एतत् (यह), स्त्रीलिङ्ग

10. एतत् (यह), नपुंसकलिङ्ग

11. किम् (कौन), पुंल्लिङ्ग

12. किम् (कौन), स्त्रीलिङ्ग

13. किम् ( कौन), नपुंसकलिङ्ग

शेष विभक्तियों में पुल्लिग ‘किम्’ शब्द के समान रूप चलेंगे।

अभ्यासः

प्रश्न 1.
कोष्ठकात् ‘बालक’ शब्दस्य उचित-रूपेण रिक्तस्थानानि पूरयत- (कोष्ठक से ‘बालक’ शब्द के उचित रूप से रिक्त स्थान भरिए- Fill in the blanks with the suitable form of the word ‘बालक’ from the bracket.)
उदाहरण- प्रथमा – बालकाः खेलन्ति। (बालकः, बालकौ, बालकाः)
द्वितीया – किं त्वम् ___________ पश्यसि? (बालकेन, बालकस्य, बालकम्)
ततीया – रोहणः ___________ सह क्रीडति। (बालकात, बालकेन, बालकः)
चतुर्थी – सः ___________ कन्दुकम् यच्छति। (बालकम्, बालकाय, बालकान्)
पञ्चमी – मोहितः ___________ कन्दुकम् आनयति। (बालकेन, बालके, बालकात्)
षष्ठी – ___________ हस्तात् कन्दुकः पतति। (बालकस्य, बालकम्, बालकेन)
सप्तमी – कन्दुकः ___________ पतति। (बालके, बालकम्, बालकात्)
सम्बोधन – हे ___________! किं त्वम् कन्दुकेन क्रीडसि? (बालक: बालकाः, हे बालक)
उत्तरम्-
बालकम्, बालकेन, बालकाय, बालकात्, बालकस्य, बालके, हे बालक

प्रश्न 2.
कोष्ठकदत्तस्य शब्दस्य उचितरूपं लिखत- (कोष्ठक में दिए गए शब्द का उचित रूप लिखिए- Fill in the blanks with the appropriate form of the word given in bracket.)
(क) 1. ___________ (अध्यापिका-प्रथमा, ए०व०) कक्षायाम् आगच्छति।
2. छात्राः ___________ (अध्यापिका-द्वितीया, ए०व०) नमन्ति।
3. ते वदन्ति ___________ (अध्यापिका-चतुर्थी, ए०व०) नमः।
4. ___________ (वाटिका-सप्तमी, ए०व०) पुष्पाणि विकसन्ति।
5. सा ___________ (पुष्पमाला-तृतीया, ब०व०) गृहं भूषयति।
6. वृक्षस्य ___________ (शाखा-सप्तमी, ब०व०) खगाः तिष्ठन्ति।
उत्तरम्-
1. अध्यापिका
2. अध्यापिकाम्
3. अध्यापिकायै
4. वाटिकायाम्
5. पुष्पमालाभिः
6. शाखासु

(ख) 1. कालिदासः संस्कृत-साहित्यस्य प्रसिद्धः ___________ (कवि-प्रथमा, ए०व०) अभवत्।
2. पुरा अनेके ___________ (कवि-प्रथमा, ब०व०) अभवन्।
3. अभिज्ञान शाकुन्तलम् ___________ (कवि-षष्ठी, ए०व०) कालिदासस्य रचना।
4. राष्ट्रपति: ___________ (कवि-द्वितीया, ब०व०) सम्मानयति।
5. सः ___________ (कवि-चतुर्थी, ए०व०) पुरस्कारं यच्छति।
उत्तरम्-
1. कविः
2. कवयः
3. कवेः
4. कवीन्
5. कवये

प्रश्न 3.
कोष्ठकात् उचितं विकल्पं चित्वा वाक्यपूर्तिं कुरुत- (कोष्ठक से उचित विकल्प चुनकर वाक्य पूर्ति कीजिए- Pick out the correct option from the bracket and complete the sentences)
(क) 1. वने ___________ भ्रमन्ति। (पशुः पशू, पशवः)
2. सिंहः ___________ मारयति। (पशून्, पशुन्, पशूनाम्)
3. वयम् ___________ आदेशं पालयामः। (गुरुभ्यः, गुरोः, गुरुम्)
4. कोकिलः ___________ कूजति। (वसन्तऋते, वसन्तुऋतुम्, वसन्त-ऋतौ)
5. ___________ दर्शनम् पुण्यम्। (साधुनाम्, साधूनाम्, साधवः)
उत्तरम्-
1. पशवः
2. पशून्
3. गुरोः
4. वसन्त-ऋतौ
5. साधूनाम्

(ख) 1. राहुलः ___________ नमति। (पिताम्, पितारम्, पितरम्)
2. ___________ पुत्रम् वदति। (पिता, पितरौ, पितरः)
3. सः ___________ चरणौ स्पृशति। (मातुः, मातस्य, मात्रस्य)
4. राहुलस्य ___________ स्नेहः अस्ति। (माते, मातरम्, मातरि)
5. सः ___________ पत्रं लिखति। (भ्रात्रे, भ्रातरम्, भ्रातुः)
उत्तरम्-
1. पितरम्
2. पिता
3. मातुः
4. मातरि
5. भ्रात्रे

प्रश्न 4.
‘मुनि’ शब्दस्य स्थाने ‘गुरु’ शब्द प्रयुज्य वाक्यानि पुनः लिखत- (‘मुनि’ शब्द के स्थान पर ‘गुरू’ शब्द का प्रयोग करके वाक्य पुनः लिखिए- Rewrite the sentences by using the word ‘गुरू’ in place of ‘मुनि’)
1. मुनिः आश्रमे आगच्छति।
2. शिष्यः मुनिं नमति।
3. सः मुनिना सह वार्ता करोति।
4. सः मुनये पुष्पमालाम् अर्पयति।
5. सः मुनेः ज्ञानं विन्दति।
6. मुनेः अन्ये शिष्याः अपि आगच्छन्ति।
7. मुनौ तेषां परम श्रद्धा वर्तते।
8. हे मुने! भवान् धन्यः अस्ति।
उत्तरम्-
1. गुरुः आश्रमे आगच्छति।
2. शिष्यः गुरुं नमति।
3. सः गुरुणा सह वार्ता करोति।
4. सः गुरवे पुष्पमालाम् अर्पयति।
5. सः गुरोः ज्ञानं विन्दति।
6. गुरोः अन्ये शिष्याः अपि आगच्छन्ति।
7. गुरौ तेषां परम श्रद्धा वर्तते।
8. हे गुरो! भवान् धन्यः अस्ति।

प्रश्न 5.
निर्देशानुसारेण शब्दरूपाणि लिखत- (निर्देशानुसार शब्द रूप लिखिए- Write the word forms as per directions given.)
1. शिशु – षष्ठी विभक्तिः ___________ ___________ ___________
2. भानु – द्वितीया विभक्तिः ___________ ___________ ___________
3. गिरि – द्वितीया विभक्तिः ___________ ___________ ___________
4. हरि – चतुर्थी विभक्तिः ___________ ___________ ___________
5. माला – तृतीया विभक्तिः ___________ ___________ ___________
उत्तरम्-
1. शिशोः शिश्वोः शिशूनाम्
2. भानुम् भानू भानून्
3. गिरिम् गिरी गिरीन्
4. हरये हरिभ्याम् हरिभ्यः
5. मालया मालाभ्याम् मालाभिः

प्रश्न 6.
मञ्जूषायाः उचितेन सर्वनामपदेन वाक्यानि पूरयत- (मञ्जूषा से उचित सर्वनाम-पद चुनकर वाक्य पूरे कीजिए- Fill in the blanks with the suitable pronoun from the box.)
ताम्, तम्, तेन, तस्मै, तस्मात्, तान्।
उदाहरणम् – शिक्षकः तम् छात्रम् प्रश्नं पृच्छति।
1. अध्यापिका ___________ छात्राम् किम् अवदत्?
2. सा ___________ छात्रान् अदण्डयत्।
3. अमितः ___________ बालकेन सह गृहम् अगच्छत्।
4. त्वं ___________ बालकात् कलमम् आनय।
5. त्वं ___________ बालकाय फलम् यच्छ।
उत्तरम्-
1. ताम्
2. तान्
3. तेन
4. तस्मात्
5. तस्मै

प्रश्न 7.
रेखाङ्कितं पदम् आधृत्य प्रश्न निर्माणं कुरुत- (रेखांकित-पद के आधार पर प्रश्न निर्माण कीजिए- Frame-questions based on the underlined word.)
कान्, केषाम्, केभ्यः, केषु, कैः, कस्मात्, के।
उदाहरण-
1. छात्राः पठन्ति।
1. के पठन्ति?

2. अध्यापिका छात्रान् पृच्छति।
2. ___________

3. उद्यानम् वृक्षैः सुन्दरम् अस्ति।
3. ___________

4. सः छात्रेभ्यः पारितोषिकानि यच्छति।
4. ___________

5. पत्राणि वृक्षात् पतन्ति।
5. ___________

6. भारतम् ऋषीणाम् देशः।
6. ___________

7. वृक्षेषु फलानि सन्ति।
7. ___________
उत्तरम्-
2. अध्यापिका कान् पृच्छति?
3. उद्यानम् कैः सुन्दरम् अस्ति?
4. सः केभ्यः पारितोषिकानि यच्छति?
5. पत्राणि कस्मात् पतन्ति?
6. भारतम् केषाम् देशः?
7. केषु फलानि सन्ति?

प्रश्न 8.
कोष्ठकात् उचितं विकल्पं चित्वा वाक्यानि पूरयत- (कोष्ठक से उचित पद चुनकर वाक्य पूरे कीजिए- Pick out the suitable word from the bracket and complete the sentences.)
1. ___________ गृहे कः वसति? (एतत्, एतस्मिन्)
2. ___________ बालिकायै पुस्तकम् यच्छ। (तस्मै, तस्यै)
3. ___________ बालकस्य गृहं कुत्र अस्ति? (एतस्य, एतस्याः)
4. ___________ लतायाम् पुष्पाणि सन्ति। (एतस्याम्, एतस्मिन्)
5. ___________ वृक्षे फलानि सन्ति। (तस्याम्, तस्मिन्)
उत्तरम्-
1. एतस्मिन्
2. तस्यै
3. एतस्य
4. एतस्याम्
5. तस्मिन्।

We have given detailed NCERT Solutions for Class 7 Sanskrit Ruchira Chapter 6 सदाचारः Questions and Answers come in handy for quickly completing your homework.

NCERT Solutions for Class 7 Sanskrit Ruchira Chapter 6 सदाचारः

Class 7 Sanskrit Chapter 6 सदाचारः Textbook Questions and Answers

प्रश्न: 1.
सर्वान् श्लोकान् सस्वरं गायत। (सभी श्लोकों को लय में गाइए। Recite all the Shlokas.)
उत्तराणि:
छात्र सुस्वर में सभी श्लोकों को गाएँ।

प्रश्न: 2.
उपयुक्तकथनानां समक्षम् ‘आम्’ अनुपयुक्तकथनानां समक्षं ‘न’ इति लिखत- (उचित कथनों के सामने ‘आम्’ और अनुचित कथनों के सामने ‘न’ लिखें- Write ‘आम्’ and ‘न’ in front of right/sentences and ‘न’ opposite the wrong ones.)

उत्तराणि:
क) आम्
(ख) न
(ग) आम्
(घ) न
(ङ) आम्।

प्रश्न: 3.
एकपदेन उत्तरत- (एक शब्द में उत्तर लिखिए- Answer in one word.)

(क) कः न प्रतीक्षते?
उत्तराणि:
मृत्युः

(ख) सत्यता कदा व्यवहारे किं स्यात्?
उत्तराणि:
सर्वदा

(ग) किं ब्रूयात्?
उत्तराणि:
सत्यम्

(घ) केन सह कलहं कृत्वा नरः सुखी न भवेत् ?
उत्तराणि:
मित्रेण

(ङ) कः महरिपुः अस्माक शरीरे तिष्ठिति?
उत्तराणि:
आलस्यम्

प्रश्न: 4.
रेखाङ्कितपदानि आधृत्य प्रश्ननिर्माणं कुरुत- (रेखांकित शब्दों के आधार पर प्रश्न निर्माण कीजिए Frame questions based on underlined words.)

(क) मृत्युः न प्रतीक्षते।
उत्तराणि:
कः न प्रतीक्षते?

(ख) कलहं कृत्वा नरः दुःखी भवति।
उत्तराणि:
किम् कृत्वा नरः दुःखी भवति?

(ग) पितरं कर्मणा सेवेत।
उत्तराणि:
कम् कर्मणा सेवेत?

(घ) व्यवहारे मृदुता श्रेयसी।
उत्तराणि:
व्यवहारे का श्रेयसी?

(ङ) सर्वदा व्यवहारे ऋजुता विधेया।
उत्तराणि:
कदा व्यवहारे ऋजुता विधेया?

प्रश्नः 5.
प्रश्नमध्ये त्रीणि क्रियापदानि सन्ति। तानि प्रयुज्य सार्थक-वाक्यानि रचयत- (प्रश्न के बीच में तीन क्रियावाचक शब्द हैं। उनको जोड़कर अर्थपूर्ण वाक्य बनाइए- There are three verbs in the centre of the question. Frame meaningful sentences by joining them.)

(क) ……………………….
(ख) ……………………….
(ग) ……………………….
(घ) ……………………….
(ङ) ……………………….
(च) ……………………….
(छ) ……………………….
(ज) ……………………….
उत्तराणि:
(क) सत्यं प्रियं च ब्रूयात्।
(ख) सत्यं अप्रियं च न ब्रूयात् ।
(ग) अनृतं प्रियं च न ब्रूयात्।
(घ) व्यवहारे कदाचन कौटिल्यं न स्यात् ।
(ङ) व्यवहारे सर्वदा औदार्यं स्यात् ।
(च) वाचा गुरुं सेवेत।
(छ) श्रेष्ठजनं कर्मणा सेवेत।
(ज) मनसा मातरं पितरं च सेवेत।

प्रश्न: 6.
मञ्जूषातः अव्ययपदानि चित्वा रिक्तस्थानानि पूरयत- (मञ्जूषा से अव्यय शब्दों को चुनकर रिक्त स्थानों की पूर्ति कीजिए- Fill in the blanks by choosing indeclinables from the box.)

तथा, न, कदाचन, सदा, च, अपि

(क) भक्तः…………….. ईश्वरं स्मरति।
उत्तराणि:
सदा

(ख) असत्यं …………….. वक्तव्यम्।
उत्तराणि:
न

(ग) प्रियं……………….. सत्यं वदेत् ।
उत्तराणि:
तथा

(घ) लता मेधा………………… विद्यालयं गच्छतः।
उत्तराणि:
च

(ङ) ………………… कुशली भवान् ?
उत्तराणि:
अपि

(च) महात्मागान्धी……………….. अहिंसां न अत्यजत्।
उत्तराणि:
कदाचन।

प्रश्न: 7.
चित्रं दृष्ट्वा मञ्जूषातः पदानि च प्रयुज्य वाक्यानि रचयत। (चित्र को देखकर और मञ्जूषा के शब्दों का प्रयोग कर वाक्य बनाइए। See the picture and make sentences with the help of words from the box.)

मञ्जूषा
| लिखति, कक्षायाम्, श्यामपट्टे, लिखन्ति, सः, पुस्तिकायाम्, शिक्षकः, छात्राः, उत्तराणि, प्रश्नम्, ते।
1. ………………………….
2. ………………………….
3. ………………………….
4. ………………………….
5. ………………………….
उत्तराणि:
1. छात्राः कक्षायाम् संस्कृतं पठन्ति।
2. शिक्षक: श्यामपट्टे प्रश्नम् लिखति।
3. ते प्रत्येक प्रश्नम् ध्यानेन पठन्ति।
4. तदा ते उत्तराणि लिखन्ति।
5. एकः छात्रः अन्य-छात्रस्य पुस्तिकायां पश्यति।

Class 7 Sanskrit Chapter 6 सदाचारः Additional Important Questions and Answers

(1) निम्नलिखित श्लोकं पठित्वा तदाधारितानां प्रश्नानाम् उत्तराणि लिखत (निम्नलिखित श्लोक को पढ़कर उस पर आधारित प्रश्नों के उत्तर दीजिए) –

आलस्यं हि मनुष्याणां शरीरस्थो महान् रिपुः।
नास्त्युद्यमसमो बन्धुः कृत्वा यं नावसीदति॥

I. एकपदेन उत्तरत- (एक पद में उत्तर दीजिए-)

1. किं महरिपुः अस्ति?
उत्तराणि:
आलस्यम्

2. आलस्यं कीदृशः महान् रिपुः अस्ति?
उत्तराणि:
शरीरस्थः

II. पूर्णवाक्येन उत्तरत-(पूर्ण वाक्य में उत्तर दीजिए-)

1. उद्यमसमः कः मनुष्याणां नास्ति?
उत्तराणि:
उद्यमसमः बन्धुः मनुष्याणां नास्ति।

2. कं कृत्वा मनुष्यः नावसीदति?
उत्तराणि:
उद्यम कृत्वा मनुष्यः नावसीदति।

III. निर्देशानुसारमेन उत्तरत (निर्देश के अनुसार उत्तर दीजिए-)

1. ‘महान् रिपुः’ अनयोः विशेषणपदं किम्?
(क) महान्
(ख) रिपुः
(ग) महत्
(घ) रिपु
उत्तराणि:
महान्

2. ‘कृत्वा’ पदे कः प्रत्ययः अस्ति?
(क) त्वा
(ख) कतवा
(ग) क्त्वा
(घ) क्तवा
उत्तराणि:
क्त्वा

(2) पर्यायपदानि लिखत (पर्यायवाची पदों को लिखिए-)

पदानि – पर्यायाः
(i) शत्रुः – बन्धुः
(ii) मानवानाम् – अवसीदति
(iii) परिश्रम – रिपुः
(iv) मित्रम् – उद्यम
(v) दुःखीयति – मनुष्याणाम्
उत्तरम्-
(i) रिपुः
(ii) मनुष्याणाम्
(iii) उद्यम
(iv) बन्धुः
(v) अवसीदति

(3) ‘क’ पदस्य श्लोकांशं ‘ख’ पदस्य श्लोकांशैः सह योजयत (‘क’ पद श्लोकांश को ‘ख’ पद के श्लोकांशों के साथ जोड़िए-)

‘क’ – ‘ख’
(i) आलस्यं हि मनुष्याणाम् – समबन्धुः
(ii) नास्ति उद्यमसमः बन्धुः – मनुष्याणाम्
(iii) शरीरस्थः – कृत्वा यं नावसीदति
(iv) आलस्यं हि – नावसीदति
(v) कृत्वा यम् – महान् रिपुः
(vi) नास्ति उद्यम – शरीरस्थो महान् रिपुः
उत्तरम्-
(i) आलस्यं हि मनुष्याणाम् – शरीरस्थो महान् रिपुः
(ii) नास्ति उद्यमसमः बन्धुः – कृत्वा यं नावसीदति
(iii) शरीरस्थः – महान् रिपुः
(iv) आलस्यं हि – मनुष्याणाम्
(v) कृत्वा यम् – नावसीदति
(v) नास्ति उद्यम – समबन्धुः

(4) परस्परमेलनम् कुरुत- (परस्पर मेल कीजिए-Match the following.)

(क) (i) पर्यायाः

ब्रूयात् – निरन्तरम्
वाचा – व्यवहारः
अनृतम् – वदेत्
सततम् – वचनेन
आचारः – असत्यम्
उत्तराणि:
ब्रूयात् – वदेत्
वाचा – वचनेन
अनृतम् – असत्यम्
सततम् – निरन्तरम्
आचारः – व्यवहारः

(ii) विपर्यायाः

सर्वदा – मरणम्
प्रियम् – अनृतता
सत्यता – अप्रियम्
श्वः – कदाचन/कदापि
जीवनम् – ह्यः
उत्तराणि:
सर्वदा – कदाचन/कदापि
प्रियम् – अप्रियम्
सत्यता – अनृतता
श्वः – ह्यः
जीवनम् – मरणम्

(ख) श्लोकांशाः
(i) श्वः कार्यमद्य कुर्वीत – एषः धर्म सनातनः।
(ii) नहि प्रतीक्षते मृत्युः – न कदापि सुखी जनः।
(iii) प्रियं चानृतं ब्रूयात् – कृतमस्य न वा कृतम्।
(iv) मित्रेण कलहं कृत्वा – पूर्वाह्ने चापराह्निकम्।
उत्तराणि:
(i) श्वः कार्यमद्य कुर्वीत – पूर्वाह्ने चापराह्निकम्।
(ii) नहि प्रतीक्षते मृत्युः – कृतमस्य न वा कृतम्।
(iii) प्रियं चानृतं ब्रूयात् – एषः धर्मः सनातनः।
(iv) मित्रेण कलहं कृत्वा – न कदापि सुखी जनः।

(5) सत्यं ब्रूयात् प्रियं ब्रूयात् न ब्रूयात् सत्यमप्रियम्।
प्रियं च नानृतं ब्रूयात् एषः धर्मः सनातनः॥
सर्वदा व्यवहारे स्यात् औदार्यं सत्यता तथा।
ऋजुता मृदुता चापि कौटिल्यं न कदाचन॥
श्लोकान् पठत प्रश्नान् च उत्तरत- (श्लोकों को पढ़कर प्रश्नों के उत्तर दीजिए- Read the shlokas and answer the questions.)

(क) एकपदेन उत्तरत –

(i) किं न ब्रूया?
(ii) व्यवहारे किं स्यात?
(iii) मृत्युः किं न करोति?
(iv) मित्रेण कलहं कृत्वा जनः कीदृशः भवति?
उत्तराणि:
(i) सत्यमप्रियम् (सत्यम् + अप्रियम्)
(ii) औदार्यम्
(ii) प्रतीक्षाम्
(iv) दु:खी

(ख) पूर्णवाक्येन उत्तरत-
(i) सनातनः धर्मः कः?
(ii) मनसा वाचा कर्मणा कं कं सेवेत?
(iii) व्यवहारे सदा किं स्यात् किं च न?
उत्तराणि:
उत्तरम्- (i) ‘प्रियं च नानृतं ब्रूयात् एषः धर्मः सनातनः।’
(ii) श्रेष्ठं जनं, गुरुं, मातरं पितरं च अपि मनसा वाचा कर्मणा सेवेत।
(iii) व्यवहारे सदा औदार्यं स्यात् तथा सत्यता, ऋजुता मृदुता चापि स्यात्; कौटिल्यं कदापि न स्यात्।

(6) मञ्जूषातः उचितम् अव्ययपदम् आदाय वाक्यपूर्तिं कुरुत- (मञ्जूषा से उचित पद लेकर वाक्यपूर्ति कीजिए- Pick out the appropriate indeclinable from the box and complete the sentences.)

सततम्, श्वः, सर्वदा, कदापि, एव

(i) अहं ………………… ग्रामं गमिष्यामि।
उत्तराणि:
श्वः

(ii) ‘सत्यम् ………………… जयते।’
उत्तराणि:
एव

(iii) योग्यः छात्रः शोभनान् अङ्कान् लब्धुम् ………………… परिश्रमं करोति।
उत्तराणि:
सततम्

(iv) सत्यवादी हरिशचन्द्रः…………………असत्यं न अवदत्।
उत्तराणि:
कदापि

(v) सः ………………… सत्यम् एव वदति स्म।
उत्तराणि:
सर्वदा।

(7) मञ्जूषायाः सहायतया श्लोकान्वयं पूरयत। (मञ्जूषा की सहायता से श्लोक का अन्वय पूरा कीजिए। Complete the prose order with help from the box.)

अपि, सत्यता, कदाचन, व्यवहारे

…………….. सर्वदा औदार्यं तथा ……………….. स्यात्; ऋजुता मृदुता च ……….. (स्यात्); कौटिल्यम् …………….. न (स्यात्)
उत्तराणि:
व्यवहारे, सत्यता, अपि, कदाचन

(1) उचित-विकल्पं चित्वा प्रश्ननिर्माणम् कुरुत- (उचित विकल्प चुनकर प्रश्न निर्माण कीजिए Pick out the correct option and make questions.)

(i) श्वः कार्यमद्य (कार्यम् + अद्य) कुर्वीत। (कुत्र, कदा, किम्)
उत्तराणि:
श्वः कार्यं कदा कुर्वीत?

(ii) व्यवहारे सर्वदा औदार्यं स्यात्। (के, कुत्र, कस्मिन्)
उत्तराणि:
कस्मिन् सर्वदा औदार्यं स्यात्?

(iii) व्यवहारे कौटिल्यं कदापि न स्यात्। (कः, का, किम्)
उत्तराणि:
व्यवहारे किम् कदापि न स्यात्?

(iv) मित्रेण कलहं न कुर्यात्। (कस्य, कः, केन)
उत्तराणि:
केन कलहं न कुर्यात्?

(v) मातरं पितरं च कर्मणा सेवेत। (कम्, किम्, कथम्)
उत्तराणि:
मातरं पितरं च कथम् सेवेत?

(2) (क) उचितेन विकल्पेन प्रत्येकं रिक्तस्थानं पूरयत- (उचित विकल्प द्वारा प्रत्येक रिक्त स्थान भरिए Fill in the blanks with correct option.)

(i) श्वः कार्यम् अद्य कुर्वीत …………….. चापराह्निकम्। (पूवाणे, मध्याह्ने, प्रातः)
उत्तराणि:
पूर्वाह्ने

(ii) प्रियं च नानृतम् ब्रूयात् एषः …………….. सनातनः (आचारः, धर्मः, देशः)
उत्तराणि:
धर्मः

(iii) नहि …………….. मृत्युः कृत्यस्य न वा कृतम्। (परिवर्जयेत्, सेवेत, प्रतीक्षते)
उत्तराणि:
प्रतीक्षते

(iv) मित्रेण …………….. कृत्वा न कदापि सुखी नरः। (कार्यम्, कौटिल्यम्, कलहम्)
उत्तराणि:
कलहम्

(v) सर्वदा …………….. स्यात् औदार्यं सत्यता तथा। ___ (देशे, व्यवहारे, मित्रे)
उत्तराणि:
व्यवहारे।

(ख) (i) मित्रेण कलहम् कृत्वा न…………….. सुखी जनः। (कदा, कदापि, सर्वदा)
उत्तराणि:
कदापि

(ii) नहि प्रतीक्षते मृत्युः कृतम् अस्य न …………….. कृतम्। (च, सततम्, वा)
उत्तराणि:
वा

(iii) ऋतुजा मृदुता चापि कौटिल्यं …………….. कदाचन। (च, वा, न)
उत्तराणि:
न

(iv) ……….. कार्यमद्य कुर्वीत। (ह्यः, अद्य, श्वः)
उत्तराणि:
श्वः

(v) मनसा वाचा कर्मणा सेवेत…………….. सदा। (तथा, चापि, सततम्)
उत्तराणि:
सततम्।