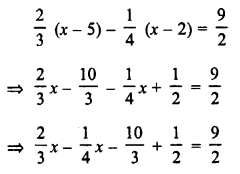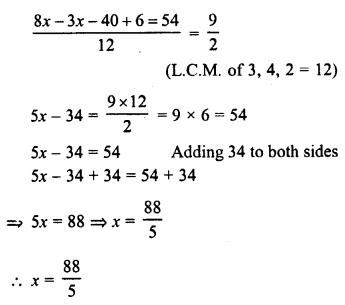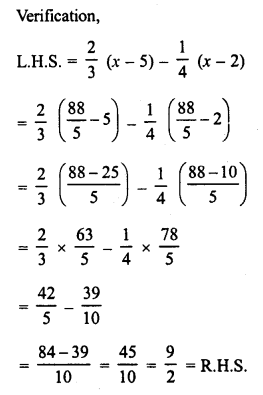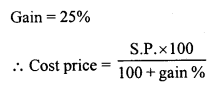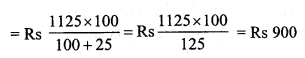Category: CBSE Class 8

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
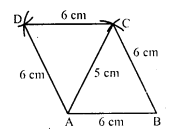
Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.0 cm, AD = 2.3 cm, AC = 4.5 cm and BD = 3.8 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 3.8 cm.
(ii) With centre A and radius 2.3 cm and with centre B and radius 3.8 cm draw arcs intersecting each other at D.

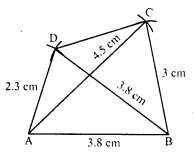
(iii) Join AD and BD.
(iv) Again with centre A and radius 4.5 cm and with centre B and radius 3 cm, draw arcs intersecting each other at C.
(v) Join AC and BC and also CD.
Then ABCD is the required quadrilateral.

Question 2.
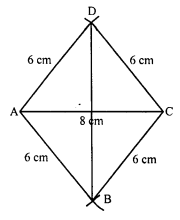
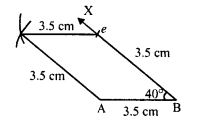
Construct a quadrilateral ABCD in which BC = 7.5 cm, AC = AD = 6 cm, CD = 5 cm and BD = 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment CD = 5 cm.

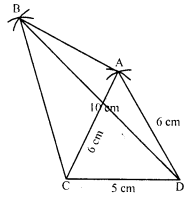
(ii) With centre C and D and radius 6 cm, draw line segments intersecting each other at A.
(iii) Join AC and AD.
(iv) Again with centre C and radius 7.5 cm and with centre D and radius 10 cm, draw arcs intersecting each other at B.
(v) Join CB, CA, DA, DB and AB.
Then ABCD is the required quadrilateral.

Question 3.
Construct a quadrilateral ABCD, when AB = 3 cm, CD = 3 cm, DA = 7.5 cm, AC = 8 cm and BD = 4 cm.
Solution:
Steps of construction :
This quadrilateral is not possible as
BD = 4 cm, AB = 3 cm and AD = 7.5 cm
The sum of any two sides of a triangle is greater than the third side.
But BD + AD = 4 + 3 = 7 cm
BD + AD < AD

Question 4.
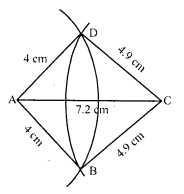
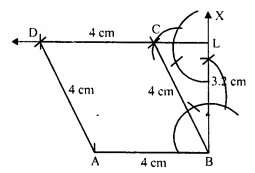
Construct a quadrilateral ABCD given AD = 3.5 cm, BC = 2.5 cm, CD = 4.1 cm, AC = 7.3 cm and BD = 3.2 cm.
Solution:
Steps of construction :
(i) Draw a line segment CD = 4.1 cm.
(ii) With centre C and radius 7.3 cm and with centre D and radius 3.5 cm, draw arcs intersecting each other at A.

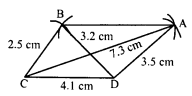
(iii) Join AC and AD.
(iv) Again with centre C and radius 2.5 cm and with centre D and radius 3.2 cm, draw arcs intersecting each other at B.
(v) Join CB’, and DB’ and join AB’.
Then ABCD is the required quadrilateral.

Question 5.
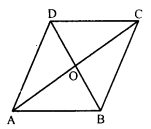
Construct a quadrilateral ABCD given AD = 5 cm, AB = 5.5 cm, BC = 2.5 cm, AC = 7.1 cm and BD = 8 cm.
Solution:
Steps of construction:
(i) Draw a line segment AB = 5 cm.

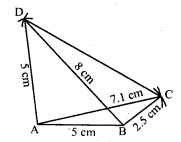
(ii) With centre A and radius 7.1 cm and with centre B and radius 2.5 cm, draw arcs which intersect each other at C.
(iii) Join AC and BC.
(iv) Again with centre A and radius 5 cm and with centre B and radius 8 cm, draw arcs which intersect each other at D.
(v) Join AD and BD and CD.
Then ABCD is the required quadrilateral.

Question 6.
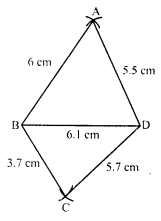
Construct a quadrilateral ABCD in which BC = 4 cm, CA = 5.6 cm, AD = 4.5 cm, CD = 5 cm and BD = 6.5 cm.
Solution:
Steps of construction:
(i) Draw a line segment CD = 5 cm.

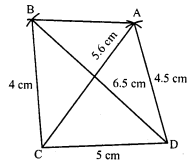
(ii) With centre C and radius 5.6 cm and with centre D and radius 4.5 cm, draw arcs which intersect each other at A.
(iii) Join AC and AD.
(iv) Again with centre C and radius 4 cm and with centre D and radius 6.5 cm, draw arcs which intersect each other at B.
(v) Join BC and BD and AB.
Then ABCD is the required quadrilateral.

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.2
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.3
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.4
• RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.5

Question 1.
Construct a quadrilateral ABCD in which AB = 4.4 cm, BC = 4 cm, CD = 6.4 cm, DA = 3.8 cm and BD = 6.6 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4.4 cm.

(ii) With centre A and radius 3.8 cm and with centre B and radius 6.6 cm, draw arcs intersecting each other at D.
(iii) With centre B and radius 4 cm, and with centre D and radius 6.4 cm, draw arcs intersecting each other at C on the other side of BD.
(iv) Join AD, BD, BC and DC.
The ABCD is the required quadrilateral.

Question 2.
Construct a quadrilateral ABCD such that AB = BC = 5.5 cm, CD = 4 cm, DA = 6.3 cm and AC = 9.4 cm. Measure BD.
Solution:
(i) Draw a line segment AC = 9.4 cm.
(ii) With centre A and C and radius 5.5 cm, draw arcs intersecting each other at B.
(iii) Join AB and CB.
(iv) Again with centre A and radius 6.3 cm, and with centre C and radius 4 cm, draw arcs intersecting each other at D below the line segment AC.

(v) Join AD and CD.
Then ABCD is the required quadrilateral. On measuring BD, it is 5 cm.

Question 3.
Construct a quadrilateral XYZW in which XY = 5 cm, YZ = 6 cm, ZW = 7 cm, WX = 3 cm and XZ = 9 cm.
Solution:
Steps of construction :
(i) Draw a line segment XZ = 9 cm.
(ii) With centre X and radius 3 cm and with centre Z and radius 7 cm, draw arcs intersecting each other at W.

(iii) Join XW and ZW.
(iv) Again with centre X and radius 5 cm and with centre Z and radius 6 cm, draw arcs, intersecting each other at Y below the line segment XZ.
(v) Join XY and ZY.
Then XYZW is the required quadrilateral.

Question 4.
Construct a parallelogram PQRS such that PQ = 5.2 cm, PR = 6.8 cm and QS = 8.2 cm.
Solution:
Steps of construction:
In a parallelogram, diagonals bisect each other. Now
(i) Draw a line segment PQ = 5.2 cm.
(ii) With centre P and radius 3.4 cm (\(\frac { 1 }{ 2 }\) of PR) and with centre Q and radius 4.1 cm (\(\frac { 1 }{ 2 }\) of QS) draw arcs intersecting each other at O.

(iii) Join PQ and QO and produced them to R and S respectively such that PO = OR and QO = OS.
(iv) Join PS, SR and RQ.
Then PQRS is the required parallelogram.

Question 5.
Construct a rhombus with side 6 cm and one diagonal 8 cm. Measure the other diagonal.
Solution:
Steps of construction :
Sides of a rhombus are equal.
(i) Draw a line segment AC = 8 cm.

(ii) With centres A and C and radius 6 cm, draw two arcs above the line segment AC and two below the line segment AC, intersecting each other at D and B respectively.
(iii) Join AB, AD, BC and CD.
Then ABCD is the required rhombus.
JoinBD.
On measuring BD, it is approximately 9 cm

Question 6.
Construct a kite ABCD in which AB = 4 cm, BC = 4.9 cm and AC = 7.2 cm.
Solution:
Steps of construction :
(i) Draw a line segment AC = 7.2 cm.

(ii) With centre A and radius 4 cm draw an arc.
(iii) With centre C and radius 4.9 cm, draw another arc which intersects the first arc at B and D.
(iv) Join AB, BC, CD and DA.
Then ABCD is the required kite.

Question 7.
Construct, if possible, a quadrilateral ABCD given, AB = 6 cm BC = 3.7 cm, CD = 5.7 cm, AD = 5.5 cm and BD = 6.1 cm. Give reasons for not being able to construct, if you cannot.
Solution:
Steps of construction :
(i) Draw a line segment BD = 6.1 cm.
(ii) With centre B and radius 6 cm and with centre D and radius 5.5 cm, draw arcs intersecting at A.
(iii) Join AB and AD.
(iv) Again with centre B and radius 3.7 cm and with centre D and radius 5.7 cm, draw two arcs intersecting each other at C below the BD.

(v) Join BC and DC.
Then ABCD is the required quadrilateral.

Question 8.
Construct, if possible a quadrilateral ABCD in which AB = 6 cm, BC = 7 cm, CD = 3 cm, AD = 5.5. cm and AC = 11 cm. Give reasons for not being able to construct, if you cannot.
Solution:
Steps of construction:
It is not possible to construct this quadrilateral ABCD because
AD + DC = 5.5 cm + 3 cm = 8.5 cm
and AC = 11 cm
AD + DC < AC.
But we know that in a triangle,
Sum of two sides is always greater than its third side.

 

Hope given RD Sharma Class 8 Solutions Chapter 18 Practical Geometry Ex 18.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Multiply:

Question 1.
(5x + 3) by (7x + 2)
Solution:
(5x + 3) x (7x + 2)
= 5x (7x + 2) + 3 (7x + 2)
= 35x² + 10x + 21x + 6
= 35x² + 31x + 6

Question 2.
(2x + 8) by (x – 3)
Solution:
(2x + 8) x (x – 3)
= 2x (x – 3) + 8 (x – 3)
= 2x² – 6x + 8x – 24
= 2x² + 2x – 24

Question 3.
(7x +y) by (x + 5y)
Solution:
(7x + y) x (x + 5y)
= 7x (x + 5y) + y (x + 5y)
= 7x² + 35xy + xy + 5y²
=7x² + 36xy + 5y²

Question 4.
(a – 1) by (0.1a² + 3)
Solution:
(a – 1) x (0.1a² + 3)
= a (0.1a² + 3) – 1 (0.1a²+ 3)
= 0.1a³ + 3a-0.1a²-3
= 0.1a³ – 0.1a² + 3a-3

Question 5.
(3x² +y²) by (2x² + 3y²)
Solution:
(3x²+y²) x (2x² + 3y²)
= 3x² (2x² + 3y²) + y²(2x² + 3y²)
= 6x^{2 +2} + 9x²y² + 2x²y² + 3y^{2 + 2}
= 6x⁴ + 11 x²y² + 3y⁴

Question 6.

Solution:

Question 7.
(x⁶-y⁶) by (x²+y²)
Solution:
(x⁶ – y⁶) x (x² + y²)
= x⁶ (x² + y²) – y⁶ (x² + y²)
= x⁶ x x² + x⁶y² – x²y⁶ -y⁶ x y²
= x^{6 + 2} + x⁶y² – x²y⁶ – y^{6 +2}
= x  + x⁶y² – x²y⁶ – y⁸

Question 8.
(x² + y²) by (3a+2b)
Solution:
(x² + y²) x (3a + 2b)
= x² (3a + 2b) + y² (3a + 2b)
= 3x²a + 2x²b + 3y²a + 2y²b
3ax² + 3av² + 2bx² + 2by²

Question 9.
[-3d + (-7ƒ)] by (5d +ƒ)
Solution:
[-3d + (-7ƒ)] x (5d +ƒ)
= -3d x (5d +ƒ) + (-7ƒ) x (5d +ƒ)
= -15d²-3dƒ- 35dƒ- 7ƒ²
= -15d² – 38dƒ- 7ƒ²

Question 10.
(0.8a – 0.5b) by (1.5a -3b)
Solution:
(0.8a – 0.5b) x (1.5a-3b)
= 0.8a x (1.5a – 36) – 0.56 (1.5a -3b)
= 1.2a² – 2.4ab – 0.75ab + 1.5b²
= 1.2a²-3.15ab+ 1.5b²

Question 11.
(2x² y² – 5xy²) by (x² -y²)
Solution:
(2x² y² – 5xy²) x (x² -y²)
= 2x²y² (x² – y²) – 5x_y² (x² – y²)
= 2x²y² x x² – 2x²y² xy²– 5xy² x x² + 5x² xy²
= 2x^{2 + 2} y²– 2x² x y^{2 + 2}– 5x¹⁺² y²+5xy^{2 + 2}
= 2x⁴y²– 2x²y⁴ – 5x³y²+ 5xy⁴

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.
(2x²-1) by (4x³ + 5x²)
Solution:
(2x²-1)x(4x³ + 5x²)
= 2x² x (4x³ + 5x²) – 1 (4x³ + 5x²)
= 2x² x 4x³ + 2x² x 5x² – 4x³ – 5x²
= 8x^{2 + 3} + 10x^{2 + 2}-4x³-5x²
= 8x⁵ + 10x⁴ – 4x³ – 5x²

Question 16.
(2xy + 3y²) (3y² – 2)
Solution:
(2xy + 3y²) (3y² – 2)
= 2xy x (3y²-2) + 3y² x (3y²-2)
= 2xy x Zy²+ 2xy x (-2) + Zy² x Zy² – Zy² x 2
= 6xy^{1 + 2}– 4xy + 9y^{2 + 2}– 6y²
= 6xy³ – 4xy + 9y⁴– 6y²
Find the following products and verify the result for x = -1, y = -2 :

Question 17.
(3x-5y)(x+y)
Solution:
(3x-5y)(x+y)
= 3x x (x + y) – 5y x (x + y)
= 3x x x + 3x x y-5y x x-5y x y
= 3x² + 3xy – 5xy – 5y²
= 3x² – 2xy – 5y²
Verfification:
x = -1,y = -2
L.H.S. = (3x-5y)(x+y)
= [3 (-1) -5 (-2)] [-1 – 2]
= (-3 + 10) (-3) = 7 x (-3) = -21
R.H.S. = 3x² – 2xy – 5y²
= 3 (-1)² – 2 (-1) (-2) -5 (-2)²
=3×1-4-5×4=3-4-20
= 3-24 = -21
∴ L.H.S. = R.H.S.

Question 18.
(x²y-1) (3-2x²y)
Solution:
(x²y-1) (3-2x²y)
= x²y (3 – 2x²y) -1(3-2x²y)
= x²y x 3 – x²y x 2x²y – 1 x 3 + 1 x 2x²y
= 3x²y-2x^{2 + 2}x y^{1 +1}-3 + 2x²y
= 3x²y – 2x⁴y²– 3 + 2x²y
= 3x²y + 2x²y – 2x⁴y² – 3
= 5x²y – 2x⁴y² – 3
Verification : (x = -1, y = -2)
L.H.S. = (x²y – 1) (3 – 2x²y)
= [(-1)² x (-2) -1] [3 – 2 x (-1)2 x (-2)]
= [1 x (-2) -1) [3 – 2 x 1 x (-2)]
= (-2 – 1) (3 + 4) = -3 x 7 = -21
R.H.S. = 5x²y – 2x⁴y² – 3
= 5 (-1)² (-2) -2 (-1)⁴ (-2)² -3
5 x 1 (-2) – 2 (1 x 4) -3
= -10-8-3 = -21
∴ L.H.S. = R.H.S

Question 19.

Solution:

Simplify :

Question 20.
x² (x + 2y) (x – 3y)
Solution:
x² (x + 2y) (x – 3y)
= x² [x (x – 3y) + 2y (x – 3y)]
= x² [x² – 3xy + 2xy – 6y²]
= x² [x² – xy – 6y²)
= x² x x² – x² x xy – x²6y²
= x⁴ – x³y – 6x²y²

Question 21.
(x² – 2y²) (x + 4y)
Solution:
(x² – 2y²) (x + 4y) x²y²
= [x² (x + 4y) -2y² (x + 4y)] x²y²
= (x³ + 4x²y – 2xy² – 8y³) x²y²
= x²y² x x³ + x²y² x 4x²y – 2x²y² x xy² – 8x²y² x y³
= x^{2 +3} y² + 4x^{2 + 2} y^{2 +1} – 2x^{2 +1} y^{2+ 2} – 8x²y²⁺³
= xy + 4⁴xy³ – 2x³y⁴ – 8x²y⁵

Question 22.
a²b² (a + 2b) (3a + b)
Solution:
a²b² (a + 2b) (3a + b)
= a²b² [a (3a + b).+ 2b (3a + b)]
= a²b² [3a² + ab + 6ab + 2b²]
= a²b² [3a² + lab + 2b²]
= a²b² x 3a² + a²b² x 7ab + a²b² x 2b²
= 3a^{2 + 2}b² + 7a²⁺¹ b²⁺¹+ 2a²b^{2 + 2}
= 3a⁴b² + 7a³b³ + 2a²b⁴

Question 23.
x² (x-y) y² (x + 2y)
Solution:
x² (x -y) y² (x + 2y)
= [x² x x – x² x y] [y² x x + y² x 2y]
= (x³ – x²y) (xy² + 2y³)
= x³ (xy² + 2y³) – x²y (xy² + 2y³)
= x³ x xy² + x³ x 2y³ – x²y x xy² – x²y x 2y³
= x^{3 +1} y² + 2x³y³ – x^{2 +1} y^{1+ 2} – 2x²y^{1 + 3}
= x⁴y² + 2x³y³ – x³y³ – 2x²y⁴
= x⁴y² + x³y³ – 2x²y⁴

Question 24.
(x³ – 2x² + 5x-7) (2x-3)
Solution:
(x³ – 2x² + 5x – 7) (2x – 3)
= (2x – 3) (x³ – 2x² + 5x – 7)
= 2x (x³ – 2x² + 5x – 7) -3 (x³ – 2x² + 5x – 7)
= 2x x x³ – 2x x 2x² + 2x x 5x – 2x x 7 -3 x x³ – 3 x (-2x²) – 3 x 5x – 3 x (-7)
= 2x⁴-4x³ + 10x²– 14x-3x³ + 6x²– 15x + 21
= 2x⁴ – 4x³ – 3x³ + 10x² + 6x²– 14x- 15x + 21
= 2x⁴-7x³ + 16x²-29x+ 21

Question 25.
(5x + 3) (x – 1) (3x – 2)
Solution:
(5x + 3) (x – 1) (3x – 2)
= (5x + 3) [x (3x – 2) -1 (3x – 2)]
= (5x + 3) [3x² – 2x – 3x + 2]
= (5x + 3) [3x² – 5x + 2]
= 5x (3x² – 5x + 2) + 3 (3x² – 5x + 2)
= (5x x 3x² – 5x x Sx + 5x x 2)+ [3 x 3x² + 3 x (-5x) + 3×2]
= 15x³ – 25x² + 10x + 9x² – 15x + 6
= 15x³ – 25x² + 9x² + 10x – 15x + 6
= 15x³ – 16x² – 5x + 6

Question 26.
(5-x) (6-5x) (2-x)
Solution:
(5-x) (6-5x) (2-x)
= [5 (6 – 5x) -x (6 – 5x)] (2 – x)
= [30 – 2$x – 6x + 5x²] (2 – x)
= (30 – 3 1x + 5x²) (2-x)
= 2 (30 – 31x + 5x²) – x (30 – 31x + 5x²)
= 60 – 62x + 10x² – 30x + 3 1x² – 5x³
= 60 – 62x – 30x + 10x² + 3 1x² – 5x³
= 60 – 92x + 41x² – 5x³

Question 27.
(2x² + 3x – 5) (3x² – 5x + 4)
Solution:
(2x² + 3x – 5) (3x² – 5x + 4)
= 2x² (3x² – 5x + 4) + 3x (3x² – 5x + 4) -5 (3x² – 5x + 4)
= 2x² x 3x² – 2x² x 5x + 2x² x 4 + 3x x 3x² – 3x x 5x + 3x x 4 – 5 x 3x² – 5 (-5x) -5×4
= 6x⁴ – 10x³ + 8x² + 9x³ – 15x² + 12x – 15x² + 25x-20
= 6x⁴ – 10x³ + 9x³ + 8x² – 15x² – 15x² + 12x + 25x – 20
= 6x⁴ – x³ – 22x² + 37x – 20

Question 28.
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
Solution:
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
= 3x (2x – 3) -2 (2x – 3) + 5x (x + 1) – 3 (x + 1)
= 6x² – 9x – 4x + 6 + 5x² + 5x – 3x – 3
= 6x² + 5x² – 9x – 4x + 5x – 3x + 6 – 3
= 11x²– 11x + 3

Question 29.
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
Solution:
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
= [5x (x + 2) -3 (x + 2)] – [2x (4x – 3) + 5 (4x – 3)]
= [5x² + 1 0x – 3x – 6] – [8x² – 6x + 20x -15]
= (5x² + 7x – 6) – (8x² + 14x – 15)
= 5x² + lx – 6 – 8x² – 14x + 15
= 5x² – 8x² + 7x – 14x – 6 + 15
= -3x² – 7x + 9

Question 30.
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
Solution:
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
= [3x (4x + 3y) + 2y (4x + 3y)]-[2x (7_x-3y)-y(7_x-3y)]
= (12x² + 9xy + 8xy + 6y²) – (14x² – 6xy – 7xy + 3y²)
= (12x² + 17xy + 6y²) – (14x² – 13xy + 3y²)
= 12x² + 17xy + 6y² – 14x² + 13xy – 3y²
= 12x² – 14x² + 17xy + 13xy + 6y² – 3y²
= -2x² + 30xy + 3y²
= -2x² + 3y² + 30xy

Question 31.
(x²-3x + 2) (5x- 2) – (3x² + 4x-5) (2x- 1)
Solution:
(x²-3x + 2) (5x- 2) – (3x² + 4x-5) (2x- 1)
= [5x (x² – 3x + 2) -2 (x² – 3x + 2)] – [2x (3x² + 4x – 5) -1 (3x² + 4x – 5)]
= [5x³ – 15x² + 10x – 2x² + 6x – 4] – [6x³ + 8x² – 10x – 3x² – 4x + 5]
= [5x³ – 15x² – 2x² + 10xc + 6x – 4] – [6x³ + 8x² – 3x² – 10x – 4x + 5]
= (5x³ – 17x² + 16x-4) – (6x³ + 5x² – 14x + 5)
= 5x³ – 17x² + 16x – 4 – 6x³ – 5x² + 14x – 5
= 5x³ – 6x³ – 17x² – 5x² + 16x + 14x – 4 – 5
= -x³ – 22x² + 30x – 9

Question 32.
x³ – 2x² + 3x – 4) (x – 1) – (2x – 3) (x² – x + 1)
Solution:
(x³ – 2x² + 3x – 4) (x – 1) – (2x – 3) (x² – x + 1)
= [x (x³ – 2x² + 3x – 4) – 1 (x³ – 2x² + 3x – 4)] – [2x (x² – x + 1) – 3 (x² – x + 1)]
= [x⁴ – 2x³ + 3x² – 4x – x³ + 2x² – 3x + 4] [2x³ – 2x² + 2x – 3x² + 3x – 3]
= (x⁴ – 2x³ – x³ + 3x² + 2x² – 4x – 3x + 4) (2x³ – 2x² – 3x² + 2x + 3x – 3)
= (x⁴ – 3x³ + 5x² – 7x + 4) – (2x³ – 5x² + 5x – 3)
= x⁴ – 3x³ + 5x² – 7x + 4 – 2x³ + 5x² – 5x + 3
= x⁴ – 3x³ – 2x³ + 5x² + 5x² – 7x – 5x + 4 + 3
= x⁴ – 5x³ + 10x² – 12x + 7

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III (Special Types of Quadrilaterals) Ex 17.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3

Question 1.
Which of the following statements are true for a rectangle ?
(i) It has two pairs of equal sides.
(ii) It has all its sides of equal length.
(iii) Its diagonals are equal.
(iv) Its diagonals bisect each other.
(v) Its diagonals are perpendicular.
(vi) Its diagonals are perpendicular and bisect each other.
(vii) Its diagonals are equal and bisect each other.
(viii) Its diagonals are equal and perpendicular, and bisect each other.
(ix) All rectangles are squares.
(x) All rhombuses are parallelograms.
(xi) All squares are rhombuses and also rectangles.
(xii) All squares are not parallelograms.
Solution:
(i) True.
(ii) False. (Only pair of opposite sides is equal)
(iii) True
(iv) True
(v) False (Diagonals are not perpendicular)
(vi) False (Diagonals are not perpendicular to each other)
(vii) True
(viii) False (Diagonals are equal but not perpendicular)
(ix) False (All rectangles are not square but a special type can be a square)
(x) True
(xi) True
(xii) False (All squares are parallelograms because their opposite sides are parallel and equal)

Question 2.
Which of the following statements are true for a square ?
(i) It is a rectangle.
(ii) It has all its sides of equal length.
(iii) Its diagonals bisect each other at right angle.
(iv) Its diagonals are equal to its sides.
Solution:
(i) True
(ii) True
(iii) True
(iv) False (Each diagonal of a square is greater than its side)

Question 3.
Fill in the blanks in each of the following so as to make the statement true :
(i) A rectangle is a parallelogram in which ……..
(ii) A square is a rhombus in which ……….
(iii) A square is a rectangle in which ………
Solution:
(i) A rectangle is a parallelogram in which one angle is right angle.
(ii) A square is a rhombus in which one angle is right angle.
(iii) A square is a rectangle in which adjacent sides are equal.

Question 4.
A window frame has one diagonal longer than the other. Is the window frame a rectangle ? Why or why not ?
Solution:
No, it is not a rectangle as rectangle has diagonals of equal length.

Question 5.
In a rectangle ABCD, prove that ∆ACB = ∆CAD.
Solution:
In rectangle ABCD, AC is its diagonal.

Now in ∆ACB and ∆CAD
AB = CD (Opposite sides of a rectangle)
BC = AD
AC = AC (Common)
∆ACB = ∆CAD (SSS condition)

Question 6.
The sides of a rectangle are in the ratio 2 : 3 and its perimeter is 20 cm. Draw the rectangle.
Solution:
Perimeter of a rectangle = 20 cm
Ratio in the sides = 2 : 3

Let breadth (l) = 2x
Then length (b) = 3x
Perimeter = 2 (l + b)
⇒ 20 = 2 (2x + 3x)
⇒ 4x + 6x = 20
⇒ 10x = 20
⇒ x = \(\frac { 20 }{ 10 }\) = 2
Length = 3x = 3 x 2 = 6
and breadth = 2x = 2 x 2 = 4 cm
Steps of construction:
(i) Draw a line segment AB = 6 cm.
(ii) At A and B draw perpendicular AX and BY.
(iii) Cut off from AX and BY,
AD = BC = 4 cm.
(iv) Join CD.
Then ABCD is the required rectangle.

Question 7.
The sides of a rectangle are the ratio 4 : 5. Find its sides if the perimeter is 90 cm.
Solution:
Perimeter of a rectangle = 90 cm.

Ratio in sides = 4 : 5
Let first side = 4x
Then second side = 5x
Perimeter = 2 (l + b)
⇒ 2 (4x + 5x) = 90
⇒ 2 x 9x = 90
⇒ 18x = 90
⇒ x = 5
First side = 4x = 4 x 5 = 20 cm
and second side = 5x = 5 x 5 = 25 cm

Question 8.
Find the length of the diagonal of a rectangle whose sides are 12 cm and 5 cm.
Solution:
In rectangle ABCD, AB = 12 cm and AD = 5 cm

BD is its diagonal.
Now, in right angled ∆ABD,
BD² = AB² + AD² (Pythagoras theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
BD = 13 cm
Length of diagonal = 13 cm

Question 9.
Draw a rectangle whose one side measures 8 cm and the length of each of whose diagonals is 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8 cm

(ii) At B, draw a perpendicular BX
(iii) With centre A and radius 10 cm, draw an arc which intersects BX at C.
(iv) With centre C and radius equal to AB and with centre A and radius equal to BC, draw arcs which intersect at D.
(v) Join AD, AC, CD and BD.
Then ABCD is the required rectangle.

Question 10.
Draw a square whose each side measures 4.8 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4.8 cm.

(ii) At A and B, draw perpendiculars AX and BY.
(iii) Cut off AD = BC = 4.8 cm
(iv) Join CD.
Then ABCD is the required square.

Question 11.
Identify all the quadrilaterals that have:
(i) Four sides of equal length.
(ii) Four right angles.
Solution:
(i) A quadrilateral whose four sides are equal can be a square or a rhombus.
(ii) A quadrilateral whose four angle are right angle each can be a square or a rectangle.

Question 12.
Explain how a square is
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle ?
Solution:
(i) A square is a quadrilateral as it has four sides and four angles.
(ii) A square is a parallelogram, because its opposite sides are parallel and equal.
(iii) A square is a rhombus because it has all sides equal and opposite sides are parallel.
(iv) A square is a rectangle as its opposite sides are equal and each angle is of 90°.

Question 13.
Name the quadrilaterals whose diagonals:
(i) bisect each other
(ii) are perpendicular bisector of each other
(iii) are equal.
Solution:
(i) A quadrilateral whose diagonals bisect each other can be a square, rectangle, rhombus or a parallelogram.
(ii) A quadrilateral whose diagonals are perpendicular bisector of each other can be a square or a rhombus.
(iii) A quadrilateral whose diagonals are equal can be a square or a rectangle.

Question 14.
ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.
Solution:
In ∆ABC, ∠B = 90°.
O is the mid-point of AC i.e. OA = OC.

BO is joined.
Now, we have to prove that OA = OB = OC
Produce BO to D such that OD = OB.
Join DC and DA.
In ∆AOB and ∆COD
OA = OC (O is the mid point of AC)
OB = OD (Construction)
∠AOB = ∠COD (Vertically opposite angles)
∆AOB = ∆COD (SAS condition)
AB = CD (c.p.c.t.) …..(i)
Similarly, we can prove that
∆BOC = ∆AOD
BC = AD …….(ii)
From (i) and (ii)
ABCD is a rectangle.
But diagonals of a rectangle bisect each other and are equal in length.
AC and BD bisect each other at O.
OA = OC = OB.
O is equidistant from A, B and C.

Question 15.
A mason has made a concrete slap. He needs it to be rectangular. In what different ways can he make sure that it is a rectangular ?
Solution:
By definition, a rectangle has each angle of 90° and their diagonals are equal.
The mason will check the slab whether it is a rectangular in shape by measuring that
(i) its each angle is 90°
(ii) its both diagonals are equal.

Hope given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III (Special Types of Quadrilaterals) Ex 17.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.1
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2
• RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.3

Question 1.
Which of the following statements are true for a rhombus ?
(i) It has two pairs of parallel sides.
(ii) It has two pairs of equal sides.
(iii) It has only two pairs of equal sides.
(iv) Two of its angles are at right angles.
(v) Its diagonals bisect each other at right angles.
(vi) Its diagonals are equal and perpendicular.
(vii) it has all its sides of equal lengths.
(viii) It is a parallelogram.
(ix) It is a quadrilateral.
(x) It can be a square.
(xi) It is a square.
Solution:
(i) True
(ii) True
(iii) False (Its all sides are equal)
(iv) False (Opposite angles are equal)
(v) True
(vi) False (Diagonals are not equal)
(vii) True
(viii) True
(ix) True
(x) True (It is a rhombus)
(xi) False

Question 2.
Fill in the blanks, in each of the following, so as to make the statement true:
(i) A rhombus is a parallelogram in which ………..
(ii) A square is a rhombus in which ………..
(iii) A rhombus has all its sides of …….. length.
(iv) The diagonals of a rhombus each ………. other at ………. angles.
(v) If the diagonals of a parallelogram bisect each other at right angles, then it is a ………..
Solution:
(i) A rhombus is a parallelogram in which adjacent sides are equal.
(ii) A square is a rhombus in which one angle is right angle.
(iii) A rhombus has all its sides of equal length.
(iv) The diagonals of a rhombus bisect each other at right angles.
(v) If the diagonals of a parallelogram bisect each other at right angles, then it is a rhombus.

Question 3.
The diagonals of a parallelogram are not perpendicular. Is it a rhombus ? Why or why not ?
Solution:
By definition of a rhombus, its diagonals bisect each other at right angle.
So, the given parallelogram is not a rhombus.

Question 4.
The diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus. If your answer is ‘No’, draw a figure to justify your answer.
Solution:
The diagonals of a quadrilateral are perpendicular to each.

It is not always possible to be a rhombus. It can be of the diagonals bisect each other at right angles and if not, then it is not rhombus as shown in the figure given above:

Question 5.
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
Solution:
In rhombus ABCD, diagonals AC and BD intersect each other at O.

∠ACB = 40°, we have to find ∠ADB.
BD || AD and AC.is its transversal..
∠ACB = ∠CAD (Alternate angles)
Now in ∆AOD
∠OAD + ∠AOD + ∠ADO = 180° (Sum of angles of a triangle)
⇒ 40° + 90° + ∠ADO = 180°
⇒ 130° + ∠ADO = 180°
⇒ ∠ADO = 180° – 130° = 50°
∠ADB = 50°

Question 6.
If the diagonals of a rhombus are 12 cm and 16 cm, find the length of each side.
Solution:
In rhombus ABCD, diagonals AC and BD bisect each other at O at right angles.

AC = 16 cm, BD = 12 cm
AO = OC = \(\frac { 16 }{ 2 }\) = 8 cm
BO = OD = \(\frac { 12 }{ 2 }\) = 6 cm.
Now, in right angled ∆AOB,
AB² = AO² + BO² = (8)² + (6)² = 64 + 36 = 100 = (10)²
AB = 10 cm
Each side of rhombus = 10 cm

Question 7.
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
Solution:
(i) Draw a line segment AC =10 cm.

(ii) Draw its perpendicular bisector and cut off OB = OD = 3 cm (\(\frac { 1 }{ 2 }\) of 6 cm).
(iii) Join AB, BC, CD and DA.
Then ABCD is the required rhombus.

Question 8.
Draw a rhombus, having each side of length 3.5 cm and one of the angles as 40°.
Solution:
Steps of construction
(i) Draw a line segment AB = 3.5 cm.

(ii) Draw a ray BX making an angle of 40° at B and cut off BC = 3.5 cm.
(iii) With centres C and A, and radius 3.5 cm. Draw arcs intersecting each other at D.
(iv) Join AD and CD.
Then ABCD is a required rhombus.

Question 9.
One side of a rhombus is of length 4 cm and the length of an altitude is 3.2 cm. Draw the rhombus.
Solution:
(i) Draw a line segment AB = 4 cm.
(ii) At B, draw a perpendicular BX and cut off BL = 3.2 cm.

(iii) At L, draw a line LY parallel to AB.
(iv) With centres B and radius 4 cm, draw an arc intersecting the line LY at C.
(v) With centre C cut off CD = 4 cm.
(vi) Join BC and AD.
Then ABCD is the required rhombus.

Question 10.
Draw a rhombus ABCD if AB = 6 cm and AC = 5 cm.
Solution:
Steps of construction :
(i) Draw a line segment AB = 6 cm.
(ii) With centre A and radius 5 cm and with centre B and radius 6 cm, draw arcs intersecting each other at C.

(iii) Join AC and BC.
(iv) Again with centres C and A and radius 6 cm, draw arcs intersecting each other at D.
(v) Join AD and CD.
Then ABCD is the required rhombus.

Question 11.
ABCD is a rhombus and its diagonals intersect at O.
(i) Is ∆BOC = ∆DOC ? State the congruence condition used ?
(ii) Also state, if ∠BCO = ∠DCO.
Solution:
In rhombus ABCD, diagonals AC and BD bisect each other at O.

(i) Now in ∆BOC and ∆DOC
OC = OC (Common)
BC = CD (Sides of rhombus)
OB = OC (Diagonals bisect each other at O)
∆BOC = ∆DOC (SSS. condition)
(ii) ∠BCO = ∠DCO

Question 12.
Show that each diagonal of a rhombus bisects the angle through which it passes:
Solution:
In rhombus ABCD, AC is its diagonal we have to prove that AC bisects ∠A and ∠C.

Now, in ∆ABC and ∆ADC
AC = AC (Common)
AB = CD (Sides of a rhombus)
BC = AD
∆ABC = ∆ADC (SSS condition)
∠BAC = ∠DAC and ∠BCA = ∠DCA (c.p.c.t.)
Hence AC bisects the angle A.
Similarly, by joining BD, we can prove that BD bisects ∠B and ∠D.
Hence each diagonal of a rhombus bisects the angle through which it passes.

Question 13.
ABCD is a rhombus whose diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, find the length of diagonal AC.
Solution:
In rhombus ABCD,

AB = 10 cm, diagonal BD = 16 cm.
Draw diagonal AC which bisects BD at O at right angle.
BO = OD = 8 cm and AO = OC.
Now in ∆AOB,
AB² = AO² + BO²
⇒ (10)² = AO² + (8)²
⇒ 100 = AO² – 64
⇒ AO² = 100 – 64 = 36 = (6)²
AO = 6.
AC = 2AO = 2 x 6 = 12 cm

Question 14.
The diagonals of a quadrilateral are of lengths 6 cm and 8 cm. If the diagonals bisect each other at right angles, what is the length of each side of the quadrilateral ?
Solution:
In a quadrilateral ABCD, diagonals AC and BD bisect each other at right angles.
AC = 8 cm and BD = 6 cm.

AO = OC = 4 cm and BO = OD = 3 cm
Now, in right ∆AOB,
AB² = AO² + BO² = (4)² + (3)² = 16 + 9 = 25 = (5)²
AB = 5 cm
Hence each side of quadrilateral will be 5 cm.

Hope given RD Sharma Class 8 Solutions Chapter 17 Understanding Shapes III Ex 17.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1

Other Exercises

• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.2
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.3
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4

Solve each of the following equations and also verify your solution :
Question 1.
9\(\frac { 1 }{ 4 }\) = y – 1\(\frac { 1 }{ 3 }\)
Solution:

Question 2.
\(\frac { 5x }{ 3 }\) + \(\frac { 2 }{ 5 }\) = 1
Solution:

Question 3.
\(\frac { x }{ 2 }\) + \(\frac { x }{ 3 }\) + \(\frac { x }{ 4 }\) = 13
Solution:

Question 4.
\(\frac { x }{ 2 }\) + \(\frac { x }{ 8 }\) = \(\frac { 1 }{ 8 }\)
Solution:

Question 5.
\(\frac { 2x }{ 3 }\) – \(\frac { 3x }{ 8 }\) = \(\frac { 7 }{ 12 }\)
Solution:

Question 6.
(x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1) = 0
Solution:
(x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1) = 0
⇒ [x² + (2 + 3) x + 2 x 3] + [x² + (-3 – 2) x + (-3) (-2)] – 2x² – 2x = 0
⇒ x² + 5x + 6 + x² – 5x + 6 – 2x² – 2x = 0
⇒ x² + x² – 2x² + 5x – 5x – 2x + 6 + 6 = 0
⇒ -2x + 12 = 0
Subtracting 12 from both sides,
-2x + 12 – 12 = 0 – 12
⇒ -2x = -12
Dividing by -2,
x = 6
Verification:
L.H.S. = (x + 2) (x + 3) + (x – 3) (x – 2) – 2x (x + 1)
= (6 + 2) (6 + 3) + (6 – 3) (6 – 2) – 2 x 6 (6 + 1)
= 8 x 9 + 3 x 4 – 12 x 7
= 72 + 12 – 84
= 84 – 84
= 0
= R.H.S.

Question 7.
\(\frac { x }{ 2 }\) – \(\frac { 4 }{ 5 }\) + \(\frac { x }{ 5 }\) +\(\frac { 3x }{ 10 }\) = \(\frac { 1 }{ 5 }\)
Solution:

Question 8.
\(\frac { 7 }{ x }\) + 35 = \(\frac { 1 }{ 10 }\)
Solution:

Question 9.
\(\frac { 2x – 1 }{ 3 }\) – \(\frac { 6x – 2 }{ 5 }\) = \(\frac { 1 }{ 3 }\)
Solution:

Question 10.
13 (y – 4) – 3 (y – 9) – 5 (y + 4) = 0
Solution:
13 (y – 4) – 3 (y – 9) – 5 (y + 4) = 0
⇒ 13y – 52 – 3y + 27 – 5y – 20 = 0
⇒ 13y – 3y – 5y – 52 + 27 – 20 = 0
⇒ 13y – 8y – 72 + 27 = 0
⇒ 5y – 45 = 0
Dividing by 5,
y = 9
Verification:
L.H.S. = 13 (y – 4) – 3 (y – 9) – 5 (y + 4)
= 13 (9 – 4) – 3 (9 – 9) – 5 (9 + 4)
= 13 x 5 – 3 x 0 – 5 x 13
= 65 – 0 – 65
= 0
= R.H.S.

Question 11.
\(\frac { 2 }{ 3 }\) (x – 5) – \(\frac { 1 }{ 4 }\) (x – 2) = \(\frac { 9 }{ 2 }\)
Solution:

Hope given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Question 1.
Identify the terms, their co-efficients for each of the following expressions.
(i) 7x²yz – 5xy
(ii) x² + x + 1
(iii)3x²y² – 5x²y² + z² + z²
(iv) 9 – ab + be-ca
(v) \(\frac { a }{ 2 } +\frac { b }{ 2 }\)-ab
(vi)2x – 0.3xy + 0.5y
Solution:
(i) Co-efficient of 7x²yz = 7
co-efficient of -5xy = -5
(ii) Co-efficient of x¹ = 1
co-efficient of x = 1
co-efficient of 1 = 1
(iii) Co-efficient of 3x²_y² = 3
co-efficient of -5x²y²z² = -5
co-efficient of z² – 1
(iv) Co-efficient of 9 = 9
co-efficient of -ab = -1
co-efficient of be = 1
co-efficient of -ca = -1
(v) Co-efficient of \(\frac { a }{ 2 } =\frac { 1 }{ 2 }\)
Co-efficient of \(\frac { b }{ 2 } =\frac { 1 }{ 2 }\)
co-efficient of -ab = -1
(vi) co-efficient of 0.2x = 0.2
co-efficient of-0.3xy = -0.3
co-efficient of 0.5y = 0.5

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any category ?
(i) x+y
(ii) 1000
(iii) x + x² + x³ + x⁴
(iv) 7 + a + 5b
(v) 2b – 3 b²    
(vi) 2y – 3y² +4y³
(vii) 5x – 4y + 3x
(viii) 4a – 15a²
(ix) xy+yz + zt + tx
(x)   pqr
(xi) p²q + pq²       
(xii)  2p + 2 q
Solution:
Monomials are (ii), (x)
Binomials are (i), (v), (viii), (xi), (xii)
Trinomials are (iv), (vi) and (vii)
None of these are (iii) and (ix)

 

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.1
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.2
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.3

Question 1.
The list price of a refrigerator is Rs 9700. If a value added tax of 6% is to be charged on it, how much one has to pay to buy the refrigerator ?
Solution:
List price of refrigerator = Rs 9700
Rate of VAT = 6%
Amount of VAT = Rs. \(\frac { 9700 x 6 }{ 100 }\) = Rs 582
Total price to be paid = Rs 9700 + 582 = Rs 10282

Question 2.
Vikram bought a watch for Rs 825. If this amount includes 10% VAT on the list price, what was the list price of the watch ?
Solution:
Price of watch including VAT = Rs 825
Rate of VAT = 10%

Question 3.
Aman bought a shirt for Rs 374.50 which includes 7% VAT. Find the list price of the shirt.
Solution:
Cost price of the shirt = Rs 374.50
Rate of VAT = 7%

Question 4.
Rani purchases a pair of shoes whose sale price is Rs 175. If he pays a VAT at the rate of 7%, how much amount does he pays as VAT. Find the net value of the pair of shoes.
Solution:
Sale price of a pair of shoes = Rs 175
Rate of VAT = 7%
Total VAT paid = Rs. \(\frac { 175 x 7 }{ 100 }\) = Rs 12.25
and total amount paid = Rs 175 + Rs 12.25 = Rs 187.25

Question 5.
Swarna paid Rs 20 as VAT on a pair of shoes worth Rs 250. Find the rate of VAT.
Solution:
Amount of VAT paid = Rs 20
Price of the pair of shoes = Rs 250
Rate of VAT = \(\frac { 20 x 100 }{ 250 }\) = 8%

Question 6.
Sarita buys goods worth Rs 5,500. She gets a rebate of 5% on it. After getting the rebate if VAT at the rate of 5% is charged, find the amount she will have to pay for the goods.
Solution:
Price of goods = Rs 5,500
Rate of rebate = 5%
Sales price after rebate

= Rs 5,225
Rate of VAT = 5%
Amount of VAT

Amount to be paid after paying VAT = Rs 5,225 + 261.25 = Rs 5486.25

Question 7.
The cost of furniture inclusive of VAT is Rs 7,150. If the rate of VAT is 10%, find the original cost of the furniture.
Solution:
Cost of furniture including VAT = Rs 7,150
Rate of VAT = 10%
Original cost of furniture

Question 8.
A refrigerator is available for Rs 13,750 including VAT. If the rate of VAT is 10%, find the original cost of refrigerator.
Solution:
Cost of refrigerator including VAT = Rs 13,750
Rate of VAT = 10%
Actual price of refrigerator

Question 9.
A colour TV is available for Rs 13,440 inclusive of VAT. If the original cost of TV is Rs 12,000, find the rate of VAT.
Solution:
Cost of TV including VAT = Rs 13,440
Actual cost = Rs 12,000
Amount of VAT = Rs 13,440 – Rs 12,000 = Rs 1,440

Question 10.
Reena goes to a shop to buy a radio, costing Rs 2,568. The rate of VAT is 7%. She tells the shopkeeper to reduce the price of the radio such that she has to pay Rs 2,568 inclusive of VAT. Find the reduction needed in the price of radio.
Solution:
Price of radio inclusive of VAT = Rs 2,568
Rate of VAT = 7%

But the cost of radio in the beginning = Rs 2,568
Reduction = Rs 2568 – Rs 2,400 = Rs 168

Question 11.
Rajat goes to a departmental store and buys the following articles :

Calculate the total amount he has to pay to the store.
Solution:
Price of 2 pairs of shoes @ Rs 800 = Rs800 x 2 = Rs 1,600
Rate of VAT = 5%


Total amount to be paid = Rs 1,680 + Rs 1,590 + Rs 1,352 = Rs 4,622

Question 12.
Ajit buys a motorcycle for Rs 17,600 including value added tax. If the rate of VAT is 10%, what is the sale price of the motorcycle ?
Solution:
Cost price of motorcycle (including VAT) = Rs 17,600
Rate of VAT = 10%
Sale price of motorcycle

Question 13.
Manoj buys a leather coat costing Rs 900 at Rs 990 after paying the VAT. Calculate the VAT charged on the cost.
Solution:
Cost price of coat = Rs 900
And sale price including VAT = Rs 990
Amount of VAT = Rs 990 – Rs 900 = Rs 90
Rate of VAT = \(\frac { 90 x 100 }{ 900 }\) = 10%

Question 14.
Rakesh goes to a departmental store and purchases the following articles:
(i) biscuits and bakery products costing Rs 50, VAT @ 5%.
(ii) medicines costing Rs 90. VAT @ 10%,
(iii) clothes costing Rs 400, VAT @ 1% and
(iv) cosmetics costing Rs 150, VAT @ 10% Calculate the total amount to be paid by Rakesh to the store.
Solution:
(i) Cost of biscuits and bakery product = Rs 50
VAT = 5%

Total amount of the bill = Rs 52.50 + Rs 99 + Rs 404 + Rs 165 = Rs 720.50

Question 15.
Rajeeta purchased a set of cosmetics. She paid Rs 165 for it including VAT. If the rate of VAT is 10%, find the sale price of the set.
Solution:
Total price of set including VAT = Rs 165
Rate of VAT = 10%

Question 16.
Sunita purchases a bicycle for Rs 660. She has paid a VAT of 10%. Find the list price of bicycle.
Solution:
Cost price of bicycle including VAT = Rs. 660
Rate of VAT = 10%

Question 17.
The sales price of a television inclusive of VAT is Rs 13,500. If VAT is charged at the rate of 8% of the list price, find the list price of the television.
Solution:
Sale price of television including VAT = Rs 13,500
Rate of VAT = 8%

Question 18.
Shikha purchased a car with a marked price of Rs 2,10,000 at a discount of 5%. If VAT is charged at the rate of 10%, find the amount Shikha had paid for purchasing the car.
Solution:
Marked price of car = Rs 2,10,000
Rate of discount = 5%

Question 19.
Sharuti bought a set of cosmetic items for Rs 345 including 15% value added tax and a purse for Rs 110 including 10% VAT. What percent is the VAT charged on the whole transactions ?
Solution:
Cost price of set = Rs 345
VAT = 15%

Question 20.
List price of a cooler is Rs 2,563. The rate of VAT is 10%. The customer requests the shopkeeper to allow a discount in the price of the cooler to such an extent that the price remains Rs 2,563 inclusive of VAT. Find the discount in the price of the cooler.
Solution:
List price of cooler = Rs. 2,563
On request the price of cooler is paid Rs 2,563 including VAT
VAT = 10%

Amount of discount = Rs 2,563 – Rs 2,330 = Rs 233

Question 21.
List price of a washing machine is Rs 9,000. If the dealer allows a discount of 5% on the cash payment, how much money will a customer pay to the dealer in cash, if the rate of VAT is 10%.
Solution:
List price of washing machine = Rs 9,000
Rate of discount = 5%
Amount after giving discount

Hope given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.3

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.3

Other Exercises

• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.1
• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.2
• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.3

Solve each of the following cryptarithms.
Question 1.

Solution:

Values of A and B be from 0 to 9 In ten’s digit 3 + A = 9
∴ A = 6 or less.
∴ 7 + B = A = 6 or less
∴ 7 + 9 or 8 = 16 or 15
∴ But it is two digit number
B = 8
Then A = 5

Question 2.

Solution:
Values of A and B can be between 0 and 9
In tens digit, A + 3 = 9
∴ A = 9 – 3 = 6 or less than 6
In ones unit B + 7 = A = 6or less
∴ 7 + 9 or 8 = 16 or 15
But it is two digit number
∴ B = 8 and
∴ A = 5

Question 3.

Solution:

Value of A and B can be between 0 and 9 In units place.
1+B = 0 ⇒1+B = 10
∴ B = 10 – 1 = 9
and in tens place
1 + A + 1 = B ⇒ A + 2 = 9
⇒ A = 9 – 2 = 7

Question 4.

Solution:
Values of A and.B can be between 0 and 9
In units place, B+1 = 8 ⇒ B = 8-1=7
In tens place A + B= 1 or A + B = 11
⇒ A + 7 = 11 ⇒ A =11-7 = 4

Question 5.

Solution:

Values of A and B can be between 0 and 9
In tens place, 2 + A = 0 or 2 + A=10
A = 10-2 = 8
In units place, A + B = 9
⇒ 8 + B = 9 ⇒ B = 9- 8 = 1

Question 6.

Solution:

Values of A and B can be between 0 and 9
In hundreds place,

Question 7.
Show that cryptarithm 4 x \(\overline { AB } =\overline { CAB }\) does not have any solution.
Solution:

It means that 4 x B is a numebr whose units digit is B
Clearly, there is no such digit
Hence the given cryptarithm has no solution.

Hope given RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.1
• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.2
• RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.3

Question 1.
Given that the number  \(\overline{35 a 64}\) is divisible by 3, where a is a digit, what are the possible volues of a ?
Solution:
The number \(\overline{35 a 64}\) is divisible by 3
∵The sum of its digits will also be divisible by 3
∴ 3 + 5 + a + b + 4 is divisible by 3
⇒ 18 + a is divisible by 3
⇒ a is divisible by 3 (∵ 18 is divisible by 3)
∴ Values of a can be, 0, 3, 6, 9

Question 2.
If x is a digit such that the number \(\overline { 18×71 }\) is divisible by 3,’ find possible values of x.
Solution:
∵ The number \(\overline { 18×71 }\)
is divisible by 3
∴ The sum of its digits will also be divisible by 3
⇒ l + 8+ x + 7 + 1 is divisible by 3
⇒ 17 + x is divisible by 3
The sum greater than 17, can be 18, 21, 24, 27…………
∴ x can be 1, 4, 7 which are divisible by 3.

Question 3.
If is a digit of the number \(\overline { 66784x }\) such that it is divisible by 9, find the possible values of x.
Solution:
∵ The number 66784 x is divisible by 9
∴ The sum of its digits will also be divisible by 9
⇒ 6+6+7+8+4+x is divisible by 9
⇒ 31 + x is divisible by 9
Sum greater than 31, are 36, 45, 54………
which are divisible by 9
∴ Values of x can be 5 on 9
∴ x = 5

Question 4.
Given that the number \(\overline { 67 y 19 }\) is divisible by 9, where y is a digit, what are the possible values of y ?
Solution:
∵ The number \(\overline { 67 y 19 }\) is divisible by 9
∴The sum of its digits will also be divisible by 9
⇒ 6 + 7+ y+ 1+ 9 is divisible by 9
⇒ 23 + y is divisible by 9
∴ The numbers greater than 23 are 27, 36, 45,……..
Which are divisible by 9
∴y = A

Question 5.
If \(\overline { 3 x 2 }\) is a multiple of 11, where .v is a digit, what is the value of * ?
Solution:
∵ The number \(\overline { 3 x 2 }\) is multiple of 11
∴ It is divisible by 11
∴ Difference of the sum of its alternate digits is zero or multiple of 11
∴ Difference of (2 + 3) and * is zero or multiple of 11
⇒ If x – (2 + 3) = 0 ⇒ x-5 = 0
Then x = 5

Question 6.
If \(\overline { 98125 x 2 }\) is a number with x as its tens digits such that it is divisible by 4. Find all the possible values of x.
Solution:
∵ The number \(\overline { 98125 x 2 }\) is divisible by 4
∴ The number formed by tens digit and units digit will also be divisible by 4
∴ \(\overline { x2 }\) is divisible by 4
∴ Possible number can be 12, 32, 52, 72, 92
∴ Value of x will be 1,3, 5, 7, 9

Question 7.
If x denotes the digit at hundreds place of the number \(\overline { 67 x 19 }\) such that the
number is divisible by 11. Find all possible values of x.
Solution:
∵ The number \(\overline { 67 x 19 }\) is divisible by 11
∴ The difference of the sums its alternate digits will be 0 or divisible by 11
∴ Difference of (9 + x + 6) and (1 + 7) is zero or divisible by 11
⇒ 15+x-8 = 0, or multiple of 11,
7 + x = 0 ⇒ x = -7, which is not possible
∴ 7 + x = 11, 7 + x = 22 etc.
⇒ x=11-7 = 4, x = 22 – 7
⇒ x = 15 which is not a digit
∴ x = 4

Question 8.
Find the remainder when 981547 is divided by 5. Do this without doing actual division.
Solution:
A number is divisible by 5 if its units digit is 0 or 5
But in number 981547, units digit is 7
∴ Dividing the number by 5,
Then remainder will be 7 – 5 = 2

Question 9.
Find the remainder when 51439786 is divided by 3. Do this without performing actual division.
Solution:
In the number 51439786, sum of digits is 5 + 1+ 4 + 3 + 9 + 7 + 8 + 6 = 43 and the given number is divided by 3.
∴ The sum of digits must by divisible by 3
∴ Dividing 43 by 3, the remainder will be = 1
Hence remainder = 1

Question 10.
Find the remainder, without performing actual division when 798 is divided by 11.
Solution:
Let n = 798 = a multiple of 11 + [7 + 8 – 9] 798 = a multiple of 11 + 6
∴ Remainder = 6

Question 11.
Without performing actual division, find the remainder when 928174653 is divided by 11.
Solution:
Let n = 928174653
= A multiple of 11+(9 + 8 + 7 + 6 + 3)-(2 + 1+4 + 5)
= A multiple of 11 + 33 – 12
= A multiple of 11 + 21
= A multiple of 11 + 11 + 10
= A multiple of 11 + 10
∴ Remainder =10

Question 12.
Given an example of a number which is divisible by :
(i) 2 but not by 4.
(ii) 3 but not by 6.
(iii) 4 but not by 8.
(iv) both 4 and 8 but not 32.
Solution:
(i) 2 but not by 4
A number is divisible by 2 if units do given is even but it is divisible by 4 if the number formed by tens digit and ones digit is divisible by 4.
∴ The number can be 222, 342 etc.
(ii) 3 but not by 6
A number is divisible by 3 if the sum of its digits is divisible by 3
But a number is divisible by 6, if it is divided by 2 and 3 both
∴ The numbers can be 333, 201 etc.
(iii) 4 but not by 8
A number is divisible by 4 if the number formed by the tens digit and ones digit is divisible by 4 but a number is divisible by 8, if the number formed by hundreds digit, tens digit and ones digit is divisible by 8.
∴ The number can be 244, 1356 etc.
(iv) Both 4 and 8 but not by 32
A number in which the number formed by the hundreds, tens and one’s digit, is divisible by 8 is divisible by 8. It will also divisible by 4 also.
But a number when is divisible by, 4 and 8 both is not necessarily divisible by 32 e.g., 328, 5400 etc.

Question 13.
Which of the following statements are true ?
(i) If a number is divisible by 3, it must be divisible by 9.
(ii) If a number is divisible by 9, it must be divisible by 3.
(iii) If a number is divisible by 4, it must be divisible by 8.
(iv) If a number is divisible by 8, it must be divisible by 4.
(v) A number is divisible by 18, if it is divisible by both 3 and 6.
(vi) If a number is divisible by both 9 and 10, it must be divisible by 90.
(vii) If a number exactly divides the sum of two numbers, it must exactly divide the numbers separately.
(viii) If a number divides three numbers exactly, it must divide their sum exactly.
(ix) If two numbers are co-priirie, at least one of them must be a prime number.
(x) The sum of two consecutive odd numbers is always divisible by 4.
Solution:
(i) False, it is not necessarily that it must divide by 9.
(ii) Trae.
(iii) False, it is not necessarily that it must divide by 8.
(iv) True.
(v) False, it must be divisible by 9 and 2 both.
(vi) True.
(vii) False, it is not necessarily.
(viii)True.
(ix) False. It is not necessarily.
(x) True.

Hope given RD Sharma Class 8 Solutions Chapter 5 Playing With Numbers Ex 5.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax (VAT) Ex 13.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.1
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.2
• RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.3

Question 1.
Find the S.P. If
(i) M.P. = Rs. 1300 and Discount = 10%
(ii) M.P. = Rs. 500 and Discount = 15%
Solution:
(i) M.P. = Rs. 1300, Discount = 10%

Question 2.
Find the M.P. If
(i) S.P. = Rs. 1222 and Discount = 6%
(ii) S.P. = Rs. 495 and Discount = 1%
Solution:
(i) S.P. = Rs. 1222, discount = 6%

Question 3.
Find discount in percent when
(i) M.P. = Rs. 900 and S.P. = Rs. 873
(ii) M.P. = Rs. 500 and S.P. = Rs. 425
Solution:
(i) M.P. = Rs. 900
S.P. = Rs. 873
Discount = M.P. – S.P. = Rs. 900 – Rs. 873 = Rs. 27

(ii) M.P. = Rs. 500
S.P. = Rs. 425
Discount M.P. – S.P. = Rs. 500 – Rs. 425 = = Rs. 75

Question 4.
A shop selling sewing machines offers 3% discount on ail cash purchases. What cash amount does a customer pay for a sewing machine, the price of which is marked as Rs. 650.
Solution:
Marked price (M.P.) of one sewing machine = Rs. 650
Rate of discount = 3%

Question 5.
The marked price of a ceiling fan is Rs. 720. During off season, it is sold for Rs. 684. Determine the discount percent.
Solution:
Marked price (M.P.) of fan = Rs. 720
Sale price (S.P.) = Rs. 684
Amount of discount = M.P. – S.P. = Rs. 720 – Rs. 684 = Rs. 36

Question 6.
On the eve of Gandhi Jayanti, a saree is sold for Rs. 720 after allowing 20% discount. What is the marked price ?
Solution:
S.P. of saree = Rs. 720
Rate of discount = 20%

Question 7.
After allowing a discount of 7\(\frac { 1 }{ 2 }\) % on the marked price, an article is sold for Rs. 555. Find its marked price.
Solution:
Selling price (S.P.) = Rs. 555

Question 8.
A shopkeeper allows his customers 10% off on the marked price of goods and still gets a profit of 25%. What is the actual cost to him of an article marked Rs. 250?
Solution:
Marked price = Rs. 250
Discount allowed = 10%

Question 9.
A shopkeeper allows 20% off on the marked price of goods and still gets a profit of 25%. What is the actual cost to him of an article marked Rs. 500 ?
Solution:
Marked price (M.P.) of an article = Rs. 500
Discount allowed = 20%
Selling price (S.P.)

Question 10.
A tradesman marks his goods at such a price that after allowing a discount of 15%, he makes a profit of 20%. What is the marked price of an article whose cost price is Rs 170 ?
Solution:
Rate of discount = 15% gain = 20%
Cost price (C.P.) of an article = Rs 170
Selling price (S.P.)

Question 11.
A shopkeeper marks his goods in such a way that after allowing a discount of 25% on the marked price, he still makes a profit of 50%. Find the ratio of the C.P. to the M.P.
Solution:
Let cost price (C.P.) = Rs 100
Profit = 50%
Selling Price (S.P.)

Question 12.
A cycle dealer offers a discount of 10% and still makes a profit of 26%. What is the actual cost to him of a cycle whose marked price is Rs 840 ?
Solution:
Rate of discount = 10%
Gain = 26%
Marked Price (M.P.) = Rs 840
Selling Price (S.P.)

Question 13.
A shopkeeper allows 23% commission on his advertised price and still makes a profit of 10%. If he gains Rs 56 on one item, find his advertised price.
Solution:
Rate of commission = 23%
Profit = 10%
Total gain = Rs 56

Question 14.
A shopkeeper marks his goods at 40% above the cost price but allows a discount of 5% for cash payment to his customers. What actual profit does he make, if he receives Rs 1064 after paying the discount ?
Solution:
Let cost price (C.P.) = Rs 100
Marked price = Rs 100 + 40 = Rs 140
Rate of discount = 5%
Selling price (S.P)

Question 15.
By selling a pair of ear rings at a discount of 25% on the marked price, a jeweller makes a profit of 16%. If the profit is Rs 48, what is the cost price ? What is the marked price and the price at which the pair was eventually bought ?
Solution:
Total profit = Rs 48
Profit percent = 16%
Cost price = \(\frac { 48 x 100 }{ 16 }\) = Rs 300
Selling Price = C.P. + profit = Rs 300 + Rs 48 = Rs 348
Rate of discount = 25%

Question 16.
A publisher gives 32% discount on the printed price of a book to booksellers. What does a bookseller pay for a book whose printed price is Rs 275 ?
Solution:
Printed price of a book = Rs 275
Rate of discount = 32%
Selling price (S.P.)

Question 17.
After allowing a discount of 20% on the marked price of a lamp, a trader loses 10%. By what percentage is the marked price above the cost price ?
Solution:
Rate of discount = 20%
Loss = 10%
Let the cost price of the lamp = Rs 100
Loss = 10%
Selling price = Rs 100 – 10 = Rs 90
Rate of discount = 20%

Question 18.
The list price of a table fan is Rs 480 and it is available to a retailer at 25% discount. For how much should a retailer sell it to gain 15% ?
Solution:
List price of table fan (M.P.) = Rs 480
Rate of discount = 25%
Selling price (S.P)

Question 19.
Rohit buys an item at 25% discount on the marked price. He sells it for Rs 660, making a profit of 10%. What is the marked price of the item ?
Solution:
Rate of discount = 25%
Selling price (S.P.) for Rohit = Rs 660
Profit = 10%

Question 20.
A cycle merchant allows 20% discount on the marked price of the cycles and still makes a profit of 20%. If he gains Rs 360 over the sale of one cycle, find the marked price of the cycle.
Solution:
Rate of discount = 20%
Profit = 20%
Total gain = Rs 360

Question 21.
Jyoti and Meena run a ready-made garment shop. They mark the garments at such a price that even after allowing a discount of 12.5%, they make a profit of 10%. Find the marked price of a suit which costs them Rs 1470.
Solution:
Rate of discount = 12.5%
Profit = 10%
Cost price = Rs 1470

Question 22.
What price should Aslam mark on a pair of shoes ? Which costs him Rs 1200 so as to gain 12% after allowing a discount of 16% ?
Solution:
Cost price of shoes = Rs 1200
Gain = 12%

Question 23.
Jasmine allows 4% discount on the marked price of her goods and still earns a profit of 20%. What is the cost price of a shirt for her marked at Rs 850 ?
Solution:
Marked price of a shirt = Rs 850
Discount = 4%
Selling price

Question 24.
A shopkeeper offers 10% off-season discount to the customers and still makes a profit of 26%. What is the cost price for the shopkeeper on a pair of shoes marked at Rs 1120 ?
Solution:
Marked price = Rs 1120
Rate of discount = 10%
S.P. of shoes

Question 25.
A lady shopkeeper allows her customers 10% discount on the marked price of the goods and still gets a profit of 25%. What is the cost price of a fan for her marked at Rs 1250 ?
Solution:
Marked price (M.P.) of fan = Rs 1250
Discount = 10%
S.P. of the fan

Hope given RD Sharma Class 8 Solutions Chapter 13 Profits, Loss, Discount and Value Added Tax Ex 13.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.