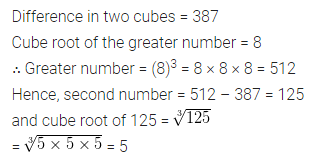Category: ICSE

Selina Publishers Concise Physics Class 8 ICSE Solutions Chapter 6 Heat Transfer

Selina Concise Physics Class 8 ICSE Solutions

Selina Publishers Concise Physics Class 8 ICSE Solutions Chapter 5 Light Energy

Selina Concise Physics Class 8 ICSE Solutions

Selina Publishers Concise Physics Class 8 ICSE Solutions Chapter 4 Energy

Selina Concise Physics Class 8 ICSE Solutions

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 5 Playing with Numbers Check Your Progress

Question 1.
In a 2-digit number, sum of digits is 7. If the difference of 2 digit number and number obtained by reversing the digits is 9, then find the number.
Solution:

Question 2.
In a 3 digit number, the difference of hundred’s digit and unit’s digit is 5. Find the quotient when difference of 3-digit number and number obtained by reversing the digits is divided by 9.
Solution:

Question 3.
Without actual calculation, write the quotient when sum of 3 digit numbers 567, 675 and 756 is divided by
(i) 111
(ii) 18
(iii) 37
(iv) 3
Solution:

Question 4.
Find the values of the letters in each of the following and give reasons for the steps involved:

Solution:

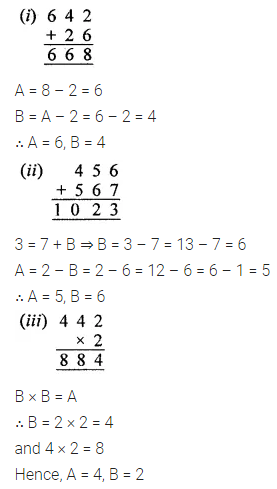
Question 5.
If 923×783 is divisible by 11, what is the value of digit x?
Solution:

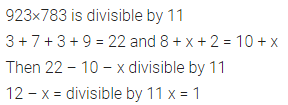
Question 6.
Check the divisibility of following numbers by 2, 3, 9 and 11:
(i) 76543
(ii) 65432
(iii) 98765436
(iv) 234567
Solution:

Question 7.
Check the divisibility of the following numbers by 5 or 10:
(i) 23565
(ii) 45270
Solution:

Question 8.
Check the divisibility of the following numbers by 4 or 8:
(i) 47596
(ii) 593024
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 5 Playing with Numbers Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) The sum of a 2-digit number and number obtained by reversing the digits is always divisible by 11 and ……….
(ii) The difference of a 2-digit number and number obtained by reversing the digits is always divisible by ………. and ……….
(iii) The difference of a 3=digit number a b c (a > c) and the number obtained by reversing the digits is always divisible by ………. and ……….
(iv) The next number of the series 0, 1, 1, 2, 3, 5, 8, 13, ………. is ……….
(v) General form of a 2 digit number 57 is ……….
(vi) Usual form of number 100 × 7 + 10 × 4 + 1 is ……….
(vii) If the division N ÷ 5 leaves remainder 4 and the division N ÷ 2 leaves remainder 1, then unit’s digit of N must be ……….
(viii)If 213×52 is divisible by 9, then digit x is ……….
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) If the division N ÷ 5 leaves a remainder 4, then unit’s digit of N may be 1 or 6.
(ii) If the division N ÷ 2 leaves a remainder 1, then unit’s digit of N may be 1, 3, 5, 7 or 9.
(iii) If a number is divisible by any number m, then it will also be divisible by each of the factors of m.
(iv) If a number is divisible by sum of two numbers then it will also be divisible by each of the two numbers separately.
(v) If 3651x is divisble by 9, then value of digit x is 3.
(vi) If 42×7 is divisible by 3, then value of digit x is 4.
(vii) The number 152875 is divisible by 9.
(viii)The number 389072 is divisible by 8.
(ix) The number 27402 is divisible by 6.
(x) The number 359249 is not divisible by 11.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 13):
Question 3.
When the sum of a 2-digit number ab and number obtained by reversing the digits is divided by (a + b), the quotient is
(a) a – b
(b) 9
(c) 11
(d) None of these
Solution:

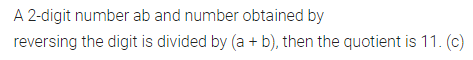
Question 4.
When the sum of a 3-digit number abc and numbers obtained by changing the order of the digits cyclically is divided by 111, then the quotient is
(a) 37
(b) a – b + c
(c) a + b + c
(d) 3
Solution:

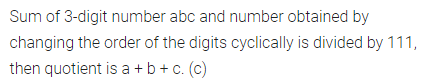
Question 5.
If A + A + A = BI, where A and B are different digits, then
(a) A = 1, B = 5
(b) A = 5, B = 2
(c) A = 5, B = 1
(d) A = 7, B = 2
Solution:

Question 6.
Which of the following numbers is not divisible by 2?
(a) 437218
(b) 437821
(c) 437812
(d) 437182
Solution:

Question 7.
Which of the following numbers is not divisible by 10?
(a) 32570
(b) 32750
(c) 32500
(d) 32075
Solution:

Question 8.
Which of the following numbers is divisible by 4?
(a) 98764
(b) 98746
(c) 98674
(d) 98647
Solution:

Question 9.
Which of the following numbers is divisible by 8?
(a) 32466
(b) 32476
(c) 32486
(d) 32456
Solution:

Question 10.
Which of the following numbers is divisible by 11?
(a) 725824
(b) 752824
(c) 725842
(d) 725482
Solution:

Question 11.
Which of the following numbers is not divisible by 9?
(a) 24354
(b) 24453
(c) 24534
(d) 24564
Solution:

Question 12.
If 467×8 is divisible by 3, then the value of x
(a) 1
(b) 2
(c) 3
(d) 4
Solution:

Question 13.
If 36x52y8 is divisible by 9, then x + y is
(a) 2
(b) 3
(c) 4
(d) 5
Solution:

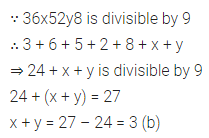
Value Based Question
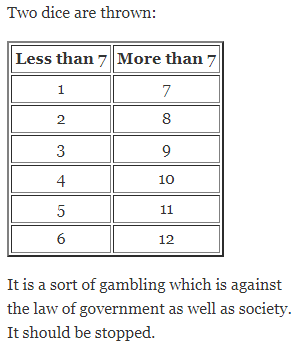
Question 1.
Rishabh plays a game with two dice in a fete. He draws three columns on a chart paper. In the left-most column, he writes the digits less than 7 and in the rightmost column he writes the numbers greater than 7. In the middle column, he writes digit 7 only. He offers people to keep money on any one of the columns. He throws two dice together if the sum of the digits on the two dice is less than 7, he doubles the money kept on the left-most column and collect the money kept on the remaining two columns. Similarly, he doubles the money on a rightmost column if the sum of digits is greater than 7 and triples on the middle column if the sum of the digits is 7. What digits should he write on leftmost and rightmost columns?
Is this game a sort of gambling? Is gambling a good way of earning money?
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
If the difference of two-digit number and number obtained by reversing the digits is 45, then write all possible 2-digit numbers.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 5 Playing with Numbers Ex 5.3

Question 1.
Which of the following numbers are divisible by 5 or by 10:
(i) 87035
(ii) 75060
(iii) 9685
(iv) 10730
Solution:

Question 2.
Which of the following numbers are divisible by 2, 4 or 8:
(i) 67894
(ii) 5673244
(iii) 9685048
(iv) 6533142
(v) 75379
Solution:

Question 3.
Which of the following numbers are divisible by 3 or 9:
(i) 45639
(ii) 301248
(iii) 567081
(iv) 345903
(v) 345046
Solution:

Question 4.
Which of the following numbers are divisible by 11:
(i) 10835
(ii) 380237
(iii) 504670
(iv) 28248
Solution:

Question 5.
Which of the following numbers are divisible by 6:
(i)15414
(ii) 213888
(iii) 469876
Solution:

Question 6.
Which of the following numbers are divisible by 7:
(i) 46f8894875
(ii) 3794856
(iii) 39823
Solution:

Question 7.
(i) If 34x is a multiple of 3, where x is a digit, what is the value of x?
(ii) If 74×5284 is a multiple of 3, where x is a digit, find the value(s) of x.
Solution:

Question 8.
If 42z3 is a multiple of 9, where z is a digit, what is the value of z?
Solution:

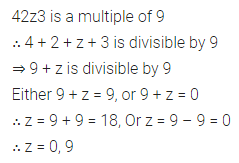
Question 9.
In each of the following replace * by a digit so that the number formed is divisible by 9:
(i) 49 * 2207
(ii) 5938 * 623
Solution:

Question 10.
In each of the following replace * by a digit so that the number formed is divisible by 6:
(i) 97 * 542
(ii) 709 * 94
Solution:

Question 11.
In each of the following replace * by a digit so that the number formed is divisible by 11:
(i) 64*2456
(ii) 86*6194
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 5 Playing with Numbers Ex 5.2

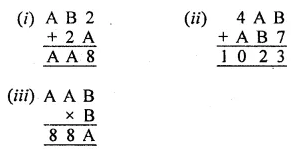
Find the values of the letters in each of the following and give reasons for the steps involved (1 to 11):
Question 1.

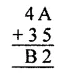
Solution:

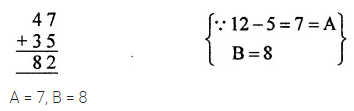
Question 2.

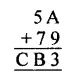
Solution:

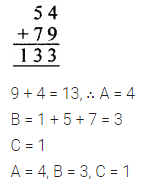
Question 3.

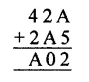
Solution:

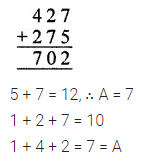
Question 4.

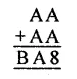
Solution:

Question 5.

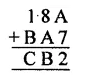
Solution:

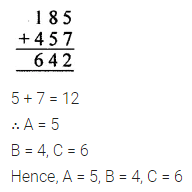
Question 6.

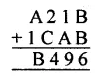
Solution:

Question 7.

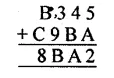
Solution:

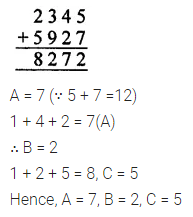
Question 8.

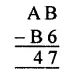
Solution:

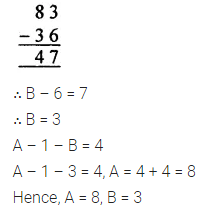
Question 9.

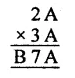
Solution:

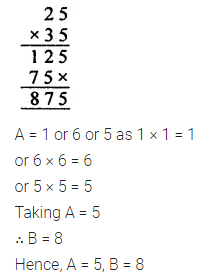
Question 10.

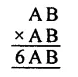
Solution:

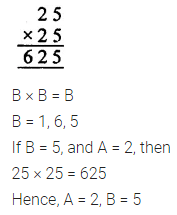
Question 11.

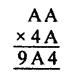
Solution:

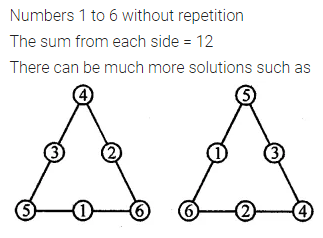
Question 12.
Fill in the numbers from 1 to 6 (without repetition) so that each side of the magic triangle adds up to 12.

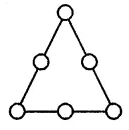
Solution:

Question 13.
Complete the magic square given alongside using number 0, 1, 2, 3, ……., 15 (only once), so that sum along each row, column and diagonal is 30.

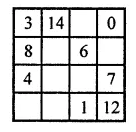
Solution:

Question 14.
Fill in the blanks to complete the following number triangle:

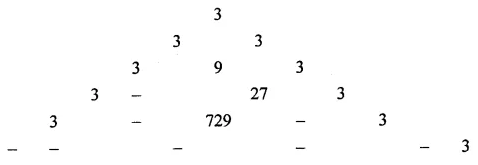
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 5 Playing with Numbers Ex 5.1

Question 1.
Write the following numbers in the generalized form:
(i) 89
(ii) 207
(iii) 369
Solution:

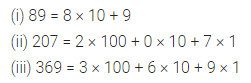
Question 2.
Write the quotient, when the sum of a 2-digit number 34 and number obtained by reversing the digits is divided by
(i) 11
(ii) sum of digits
Solution:

Question 3.
Write the quotient when the difference of a 2-digit number 73 and number obtained by reversing the digits is divided by
(i) 9
(ii) the difference of digits.
Solution:

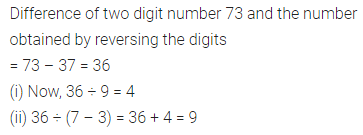
Question 4.
Without actual calculation, write the quotient when the sum of a 3-digit number abc and the number obtained by changing the order of digits cyclically i.e. bca and cab is divided by
(i) 111
(ii) (a + b + c)
(iii) 37
(iv) 3
Solution:

Question 5.
Write the quotient when the difference of a 3-digit number 843 and number obtained by reversing the digits is divided by
(i) 99
(ii) 5
Solution:

Question 6.
The sum of digits of a 2-digit number is 11. If the number obtained by reversing the digits is 9 less than the original number, find the number.
Solution:

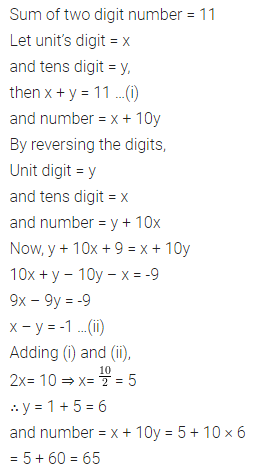
Question 7.
If the difference of a two-digit number and the number obtained by reversing the digits is 36, find the difference between the digits of the 2-digit number.
Solution:

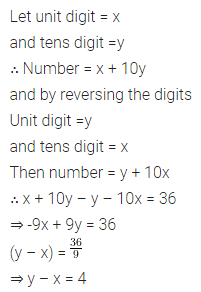
Question 8.
If the sum of two-digit number and number obtained by reversing the digits is 55, find the sum of the digits of the 2-digit number.
Solution:

Question 9.
In a 3-digit number, unit’s digit, ten’s digit and hundred’s digit are in the ratio 1 : 2 : 3. If the difference of the original number and the number obtained by reversing the digits is 594, find the number.
Solution:

Question 10.
In a 3-digit number, the unit’s digit is one more than the hundred’s digit and ten’s digit is one less than the hundred’s digit. If the sum of the original 3-digit number and numbers obtained by changing the order of digits cyclically is 2664, find the number.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 4 Cubes and Cube Roots Check Your Progress

Question 1.
Show that each of the following numbers is a perfect cube. Also, find the number whose cube is the given number:
(i) 74088
(ii) 15625
Solution:

Question 2.
Find the cube of the following numbers:
(i) -17
(ii) \(-3 \frac{4}{9}\)
Solution:

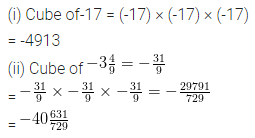
Question 3.
Find the cube root of each of the following numbers by prime factorisation:
(i) 59319
(ii) 21952
Solution:

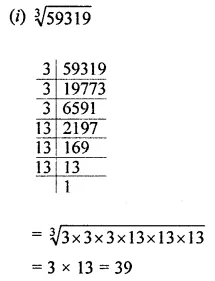
Question 4.
Find the cube root of each of the following numbers:
(i) -9261
(ii) \(2 \frac{43}{343}\)
(iii) 0.216
Solution:

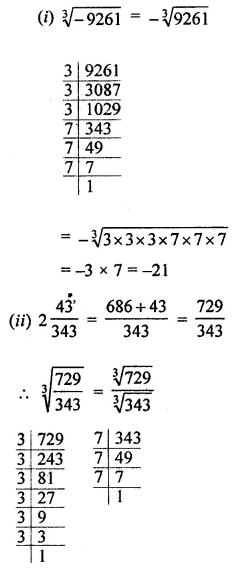
Question 5.
Find the smallest number by which 5184 should be multiplied so that product is a perfect cube. Also find the cube root of the product.
Solution:

Question 6.
Find the smallest number by which 8788 should be divided so that quotient is a perfect cube. Also, find the cube root of the quotient.
Solution:

Question 7.
Find the side of a cube whose volume is 4096 m³.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 4 Cubes and Cube Roots Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) Cube of an even natural number is …………..
(ii) Cubes of natural numbers are called …………..
(iii) Cube of a natural number whose unit digit is 7, ends with digit …………..
(iv) If a natural number has one zero at its end, then its cube will contain ………….. zero at the end.
(v) Finding a cube root is the inverse operation of finding …………..
(vi) If a number can be expressed as the triplets of equal prime factors, then it is called …………..
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) Cube of any odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a single digit number may be asingle digit number.
(vii) If a number is multiplied by 2 then its cube is multiplied by 8.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 12):
Question 3.
Cube of a negative number is
(a) negative
(b) positive
(c) negative or positive
(d) None of these.
Solution:

Question 4.
The unit digit of a cube of 476 is
(a) 4
(b) 6
(c) 8
(d) 2
Solution:

Question 5.
Cube of (-8) is
(a) -512
(b) 512
(c) -64
(d) 64
Solution:

Question 6.
Cube of \(\left(\frac{-3}{7}\right)\) is

Solution:

Question 7.
Cube root of -1331 is
(a) 11
(b) 21
(c) -11
(d) -21
Solution:

Question 8.
Cube root of 2744 is
(a) 16
(b) 18
(c) -14
(d) 14
Solution:

Question 9.
Cube root of \(1 \frac{127}{216}\) is

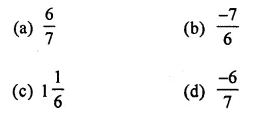
Solution:

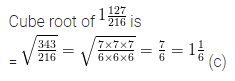
Question 10.
The smallest number by which 192 should be multiplied to make it a perfect cube is
(a) 9
(b) 6
(c) 3
(d) 2
Solution:

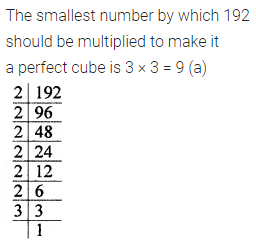
Question 11.
The smallest number by which 686 should be divided to make it a perfect cube is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:

Question 12.
The volume of a cube is 729 m³. Length of its side is
(a) 3 m
(b) 6 m
(c) 9 m
(d) 27 m
Solution:

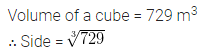
Value Based Question
Question 1.
A school decided to award prizes to their students for three values honesty, punctuality and obedience. If the number of students getting prizes for honesty, punctuality and obedience are in the ratio 1 : 2 : 3 and their product is 162, find the number of students getting prizes for each value.
Which quality you prefer to be rewarded most and why? What values are being promoted?
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
Find the volume of a cubical box if the cost of painting its outer surface is ₹1440 at the rate of ₹15 per sq. m.
Solution:

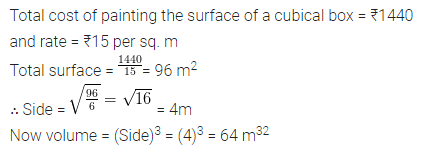
Question 2.
In a Maths lab there are some cubes and cuboids of the following measurements:
(i) one cube of side 4 cm
(ii) one cube of side 6 cm
(iii) 3 cuboids each of dimensions 4 cm × 4 cm × 6 cm and 3 cuboids each of the dimensions 4 cm × 6 cm × 6 cm.
A student wants to arrange these cubes and cuboids in the form of a big cube. Is it possible for him/her to arrange them in the form of a big cube? If yes, then find the length of side of new cube so formed.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 4 Cubes and Cube Roots Ex 4.2

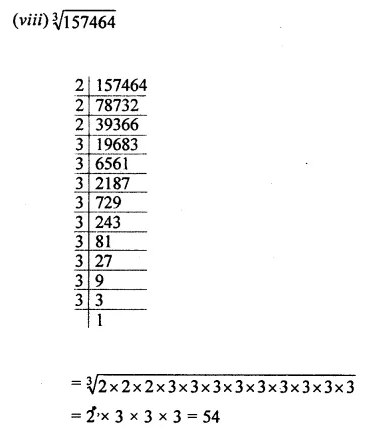
Question 1.
Find the cube root of each of the following numbers by prime factorisation:
(i) 12167
(ii) 35937
(iii) 42875
(iv) 21952
(v) 373248
(vi) 32768
(vii) 262144
(viii) 157464
Solution:

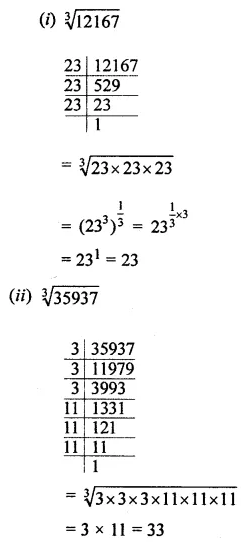
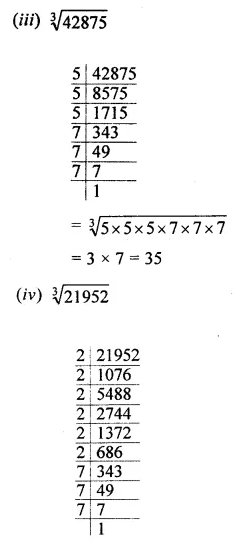
Question 2.
Find the cube root of each of the following cube numbers through estimation.
(i) 19683
(ii) 59319
(iii) 85184
(iv) 148877
Solution:

Question 3.
Find the cube root of each of the following numbers:

Solution:

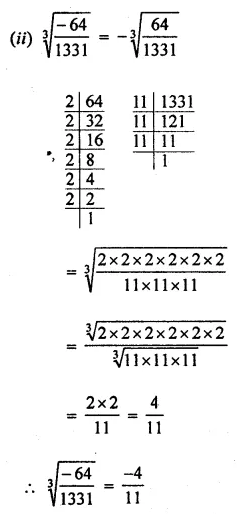
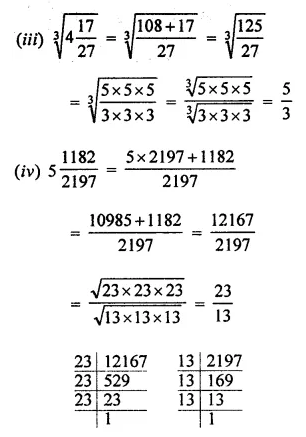
Question 4.
Evaluate the following:
(i) \(\sqrt[3]{512 \times 729}\)
(ii) \(\sqrt[3]{(-1331) \times(3375)}\)
Solution:

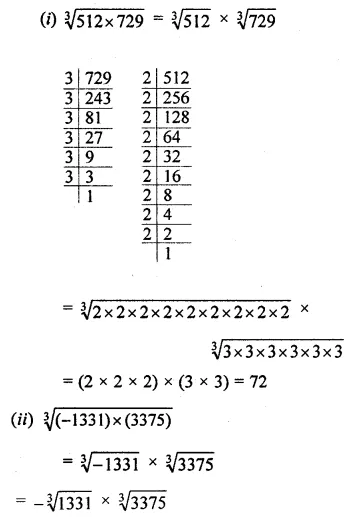
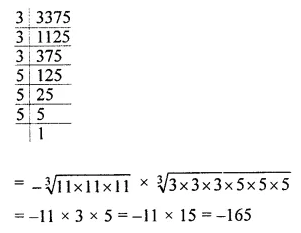
Question 5.
Find the cube root of the following decimal numbers:
(i) 0.003375
(ii) 19.683
Solution:

Question 6.
Evaluate: \(\sqrt[3]{27}+\sqrt[3]{0.008}+\sqrt[3]{0.064}\)
Solution:

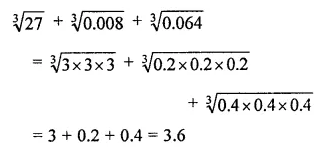
Question 7.
Multiply 6561 by the smallest number so that product is a perfect cube. Also find the cube root of the product.
Solution:

Question 8.
Divide the number 8748 by the smallest number so that the quotient is a perfect cube. Also, find the cube root of the quotient.
Solution:

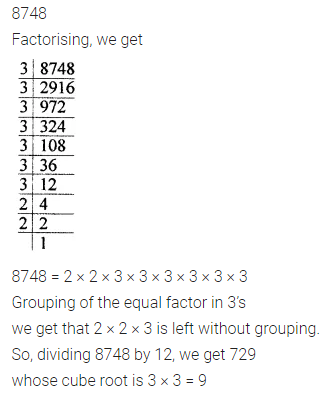
Question 9.
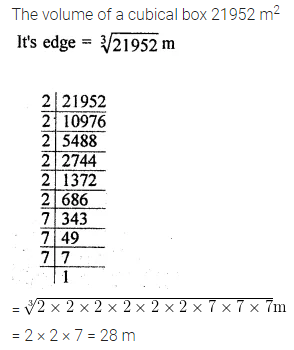
The volume of a cubical box is 21952 m³. Find the length of the side of the box.
Solution:

Question 10.
Three numbers are in the ratio 3 : 4 : 5. If their product is 480, find the numbers.
Solution:

Question 11.
Two numbers are in the ratio 4 : 5. If the difference of their cubes is 61, find the numbers.
Solution:

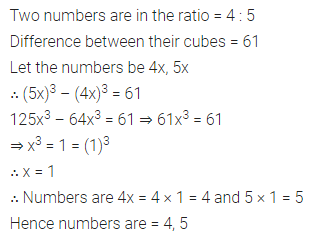
Question 12.
The difference of two perfect cubes is 387. If the cube root of the greater of two numbers is 8, find the cube root of the smaller number.
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths