CBSE Sample Papers for Class 10 Maths Basic Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 1 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.

Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.

Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.

Part – A
Section-I

Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.

Question 1.
Express 5005 as a product of its prime factors.
Solution :
5005 = 5 × 7 × 11 ×13

Question 2.
Find the zeroes of the quadratic polynomial 6x² – 3 – 7x
Solution :
Here, p (x) = 6x² – 3 – 7x = 6x² – 7x – 3
= 6x² – 9x + 2x – 3 = 3x (2x – 3) + 1  (2x – 3) +1 (2x- 1)
(2x – 3) (3x + 1)
=\(6\left(x-\frac{3}{2}\right)\left[x-\left(-\frac{1}{3}\right)\right]\)
∴ Zeroes of p (x) are \(\frac{3}{2} \text { and }-\frac{1}{3}\)

Question 3.
H.C.F and L.C.M of two numbers is 9 and 459 respectively. If one of the two numbers is 27. Find the other number. If  \(\frac{241}{4000}=\frac{241}{2^{m} 5^{n}}\) find the values of m and n, where m and n are non negative integers. Hence write its decimal expansion without actual division.
Solution :

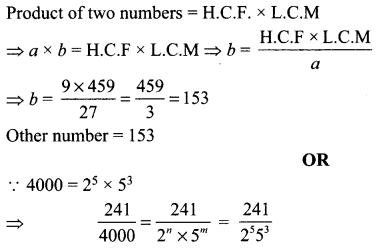
Question 4.
Find whether the pair of equations
6x – 3y + 10 = 0
and 2x-y + 9 = 0 are consistent or inconsistent.
Solution :
.

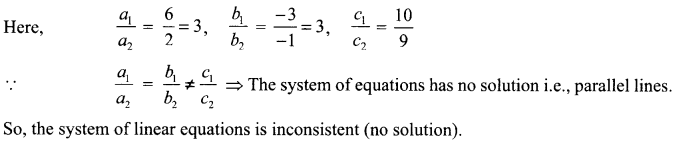Question 5.
Two numbers are in the ratio 21 : 17. If their HCF is 5, find the numbers. 1
Solution :
Let numbers be 21x and 17 x So, common factors of 21 x and 17 x = x
Also, HCF = 5
⇒ x = 5
∴ Numbers are 21 x 5 and 17 x 5 i.e.: 105 and 85.

Question 6.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of sector formed by the arc.      OR
A horse is tied to a peg at one comer of a square shaped grass field of side 15 m by means of a 5 m long rope. Find the area of that part of the field in which the horse can graze.
Solution :

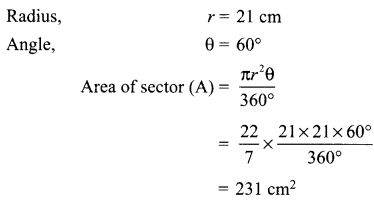
OR
Length of the rope = Radius, r = 5 m
Angle of sector = 90°
Area of the field that can graze
\(=\frac{\pi r^{2} \theta}{360^{\circ}}=\frac{22}{7} \times \frac{5 \times 5 \times 90^{\circ}}{360^{\circ}}\)
= 19.64 sq. m

Question 7.
If one diagonal of a trapezium divides the other diagonal in the ratio 1 : 2. Prove that one of the parallel sides is double the other.
OR
In ΔABC, D and E are points on sides AB and AC respectively such that DE || BC and AD : DB = 3:1. If EA = 6.6 cm then find AC.
Solution :

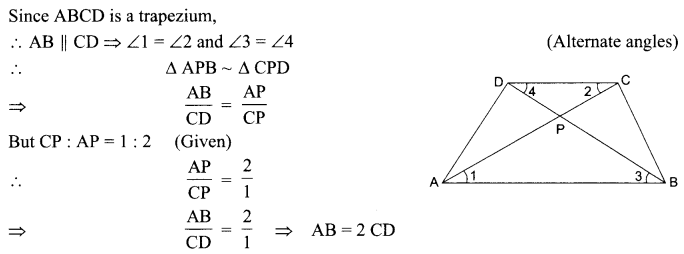
Question 8.
Two friends Mohan and Sohan drive a car. The shaded portion of the given figure represents an area swept by the wiper of the car. If OA = 7 cm and AB = 21 cm then Mohan said that area swept by the wiper is 192.5 cm². Is he right? Explain.
Solution :
Let r = 7 cm be the radius of the sector OAD and R = 7 + 21=28cm be the radius of sector OBC.
The area swept by the wiper

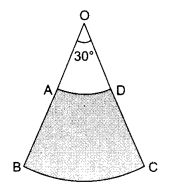
= Area of the shaded portion = Area of the sector OBC – Area of the sector OAD
\(=\pi \mathrm{R}^{2} \frac{\theta}{360^{\circ}}-\pi r^{2} \frac{\theta}{360^{\circ}}\)

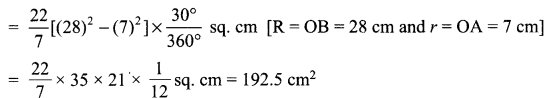
Question 9.
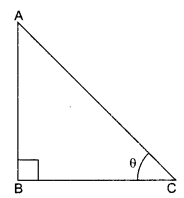
The ratio of the height of a tower and the length of its shadow on is the angle of elevation of the sun?
Solution :
Let
AB = height of the tower,
BC = length of the shadow and
∠ACB = θ = Angle of elevation of the sun

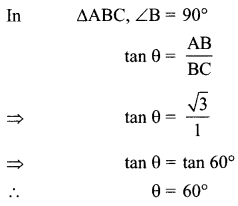
Question 10.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution :

Let the height of the cylinder = h
Radius of the cylinder (R) = 6 cm
∴ Volume of the cylinder = πR² h = n x (6)² x h
Since, Volume of the cylinder = Volume of the sphere

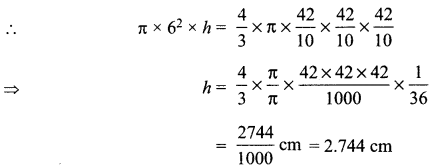
Question 11.
Find the mode for the frequency distribution table

Class	0-10	10-20	20-30	30-40	40-50	Total
Frequency	8	16	36	34	6	100

Solution :
The highest frequency is 36, which belongs to class 20 – 30.
So, it will be a modal class.

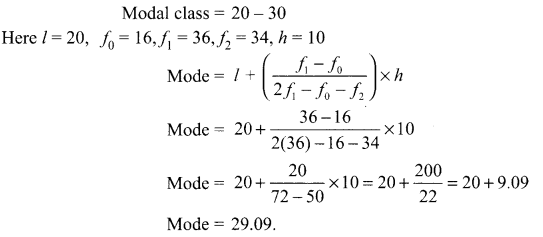
Question 12.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other a secant to the circle.
Solution :
We have the required figure.
Here, l is the given line and a circle with centre O is drawn.

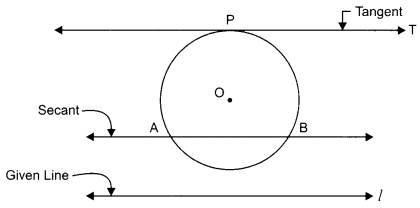
The line PT is drawn which is parallel to l and tangent to the circle.
Also, AB is drawn parallel to line l and is a secant to the circle.

Question 13.
For what value of p, the pair of linear equations
px = 2y
2x – y + 5 = 0 has unique solution?
OR
For what value of k, does the given equation (k + 1 )x² – 2(k – 1 )x + 1 = 0 have real and equal roots?
Solution :
We have:
px = 2y ⇒ px – 2y = 0
2x—y + 5=0 ⇒  2x-y = -5

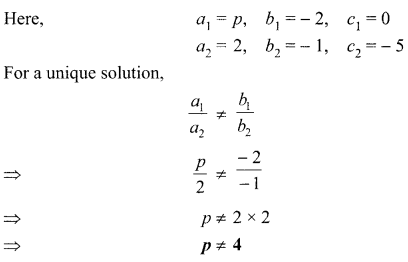
OR
(k + 1 )x² – 2(k – 1) x + 1 = 0 ⇒ a = k + 1, b = -2(k – 1), c = 1
For equal roots, b² – 4ac = 0 ⇒ [-2(k – 1)]² – 4 x (k + 1) x 1=0
⇒ 4(k – 1)² – 4{k + 1) = 0 ⇒ 4{k² + 1 – 2k) -4k-4 = 0
⇒ 4k² + 4 – 8k – 4k – 4 = 0 ⇒ 4k²-12k = 0 ⇒ 4k(k – 3) = 0
Either  4k = 0 ⇒ k = 0 or k- 3 = 0 = k = 3
Hence k= 0 or k = 3.

Question 14.
Two dice are thrown at the same time and the product of numbers appearing on them is noted. Find the probability that the product is a prime number.
OR
Two dice are thrown at the same time. Find the probability of getting different numbers on the dice.
Solution :
Now for the product of the numbers on the dice is a prime number can be in these possible ways—(1, 2), (2, 1), (1, 3), (3, 1), (5, 1), (1, 5)
So, number of possible ways = 6
∴ Required probability \(=\frac{6}{36}=\frac{1}{6}\)
OR
Since the two dice are thrown simultaneously.
Total number of outcomes = 6 x 6 = 36
Number of outcomes for getting same numbers on both dice = 6
⇒ P (same numbers) = \(\frac{6}{36}=\frac{1}{6}\)
Now, P (different numbers) + P (same numbers) = 1
⇒ P (different numbers) = 1 – P (same numbers)
\(=1-\frac{1}{6}=\frac{5}{6}\)

Question 15.
A ladder long just reaches the top of a vertical wall. If the ladder makes an angle of with the wall find the height of the wall
Solution :

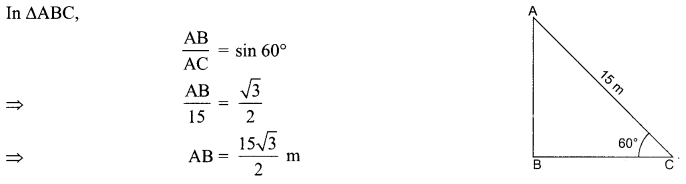
Question 16.
It is given that a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Solution :
We have P(E) + P(not E) = 1 ⇒ P(E) + 0.992 = 1
∴ P(E) = 1 – 0.992 = 0.008.

Section-II

Case study-based questions are compulsory. Attempt any 4 sub-parts from each question. Each sub-part carries 1 mark.

Case Study Based-1

Question 17.
For going to city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which is directly connect the two cities A and B. In solving such problem authority of the cities have some questions in his mind. Give answer to his following questions:

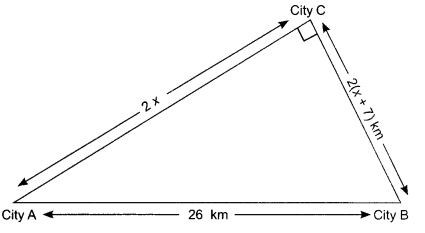
(i) Which theorem will you use to solve this problem?
(a) Pythagoras theorem
(b) Basic proportionality theorem
(c) Factor theorem
(d) Fundamental Theorem of Arithmetic

(ii) What is the distance of AC?
(a) 15 km
(b) 18 km
(c) 10 km
(d) 20 km

(iii) What is the distance of BC?
(a) 12 km
(b) 10 km
(c) 20 km
(d) 24 km

(iv) Find how much distance will be saved in reaching city B from city A after the construction of the highway.
(a) 6 km
(b) 8 km
(c) 10 km
(d) 12 km

(v) If ∠A is supposed to be 30°, then ∠B = ?
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution :
(i) (a): Pythagoras theorem

(ii) (c): 10 km
AC² + BC² = AB² ⇒ (2x)² + 2²[x + 7]² = (26)²
⇒ 4x² + 4(x² + 14x + 49) = 676
⇒  x² + 1x – 60 = 0
⇒  (x + 12)(x – 5) = 0
x = -12 or 5(x = -12 neglected as distance cannot be negative).
AC = 2x = 2 x 5 = 10 km.

(iii) (d): 24 km
x = 5
BC = 2(x + 7)
= 2(5 + 7) = 24 km

(iv) (b): 8 km
AC + CB = 10+ 24 = 34 km  AB = 26 km
Difference = 34 km – 26 km = 8 km

(v) (c): 60°
AC ⊥ BC ⇒∠C = 90°
∴ ∠A + ∠B = 90°
⇒ 30° + ∠B = 90°
∠B = 90° – 30° = 60°

Case Study Based-2

Question 18.

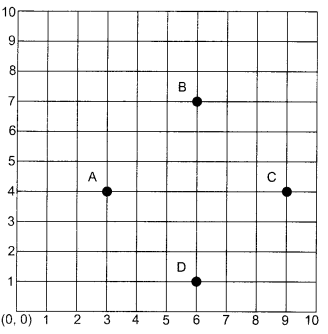
In a classroom, 4 friends have decided to seat at the points A, B, C and D as shown in fig. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli some questions which are as follows:

(i) What is the coordinates of A and B?
(a) A(3, 4), B(6, 7)
(b) A(4,3), B(7,6)
(c) A(-3, -4), B(-6, -7)
(d) A( 3, -4), B(-6, -7)

(ii) What is the coordinate of C and D?
(a) C (4, 9), D(l, 6)
(b) C (9,4),D(6,1)
(c) C (-9, -4), D(-6, -1)
(d) C(9, -4). D(6, -1)

(iii) What is the distance between AB?
(a) 2
(b) 3
(c) \(2 \sqrt{3}\)
(d) \(3 \sqrt{2}\)

(iv) What is the distance between AC?
(a) 6
(b) 4
(c) 8
(d) 10

(v) What is the distance between BD?
(a) 4
(b) 6
(c) 8
(d) 10
Solution :
(i) (a): A(3, 4), B(6, 7)
(ii) (b): C(9, 4), D(6, 1)

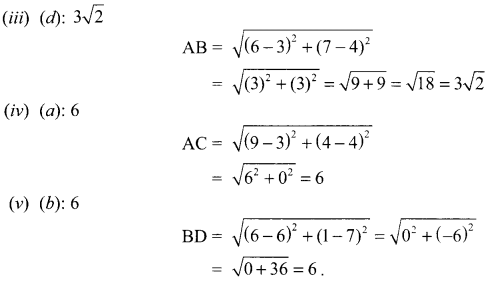
Case Study Based-3

Question 19.
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and ordered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m, and a conical upper part of same diameter and height 2.8 m. The canvas to be used costs ? 100 per sq. m. Find the amount that the associations will have to pay.

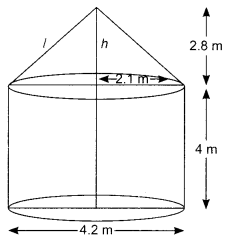
(i) Find the formula to find the volume of the cylinder.
(a) \(\pi r^{2} h\)
(b) \(\pi r^{3} h \)
(c) \(\pi r^{2} h^{2} \)
(d) \(\frac{1}{3} \pi r^{2} h\)

(ii) What is the formula for the lateral surface of the conical portion of the tent?
(a) \(\frac{1}{3} \pi r^{2} h\)
(b) \(\pi r^{2} h\)
(c) \(πrl\)
(d) \(2πrh\)

(iii) What is the volume of the tent?
(a) 85.66 cu.m
(b) 100 cu.m
(c) 225.66 cu.m
(d) 125.66 cu.m

(iv) What is the curved surface area of the tent?
(a) 75.9 sq.m
(b) 85.6 sq.m
(c) 65.9 sq.m
(d) 95.9 sq.m

(v) What is the cost of canvas to be used to cover 100 such tents from all around?
(a) ₹  580,000
(b) ₹ 379,500
(c) ₹ 448,000
(d) ₹ 279,500
Solution :
(i) (a) : \(\pi r^{2} h\)
(ii) (c): πrl
(iii) (d): 125.66 cu.m
Volume of the tent = Volume of cylindrical portion of the tent + volume of conical portion of the tent.

(iv)
(a) Curved surface area of the tent
= Lateral surface area of conical portion + curve surface area of the cylindrical portion of the tent.

Case Study Based-4

Question 20.
Due to heavy storm and rainfall, electric wire broke down on a chauraha and it disturbed the traffic. One piece of the wire is shown in the figure which followed some mathematical shape. Answer the following questions below:

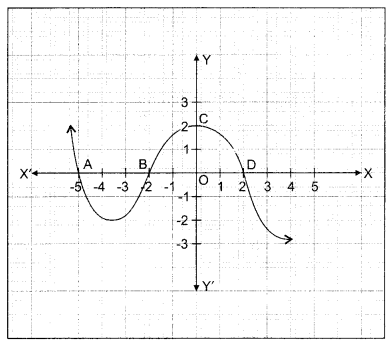
(i) Find the coordinates where does the graph cut the x-axis.
(a) (-5, 0), (-2, 0), (2, 0)
(b) (-5, 0), (-2, 0), (0, 2)
(c) (-2, 0), (0, 2), (2, 0)
(d)  (-5, 0), (0, 2), (2, 0)

(ii) Find number of zeroes of the graph y =f(x)
(a)  0
(b)  2
(c) 1
(d) 3

(iii) Find the zeroes of the graph y =f(x)
(a) -5, 0,    2
(b)  -5, -2, 2
(c) -2, 0, 2
(d) -5,   -2, 0

(iv) What will be the expression of the polynomial?
(a)  x³ +  5x² – 4x – 20
(b) x³ +    5x² + 4x – 20
(c)  x³ +   5x² + 4x + 20
(d) x³ –     5x² + 4x + 20

(v) What is the value of the polynomial if x = -5?
(a) -125
(b) 125
(c) 0
(d)  1
Solution :
(i) (a) : (-5, 0), (-2, 0), (2, 0)

(ii) (d) : 3
Since the graph v =f(x) crosses the x-axis at three different points. So, numbers of zeroes is 3.

(iii) (b): -5, -2, 2
Here graphy -fix) intersects the x-axis in (-5, 0), (-2, 0) and (2, 0). So, zeroes of f (x) are x-coordinate of these points.
∴ Zeroes of y(x) are -5, -2 and 2.

(iv) (a): x³ + 5x² – 4x – 20
∵  Zeroes of f(x) are -5, -2 and 2.
So, factors of f(x) are (x + 5)(x + 2) and (x – 2)
∴ Expression of the polynomial
= (x + 5)(x + 2)(x – 2)
= x³ + 5x² – 4x – 20.

(v) (c): 0
Put  x = -5 in /(x) = x³ + 5x² – 4x – 20
⇒ A-5) = (-5)³ + 5(-5)² – 4( 5) -20
= -125+ 125 + 20-20 = 0

Part-B
Section-III

All questions are compulsory. In case of internal choices, attempt anyone.

Question 21.
Find the fourth vertex D of a parallelogram ABCD whose three vertices are A(-2, 3), B(6, 7), and C(8, 3).
OR
If the distances of P(x,y) from the points A(3, 6) and B(-3,4) are equal, prove that 3x + y = 5.
Solution :

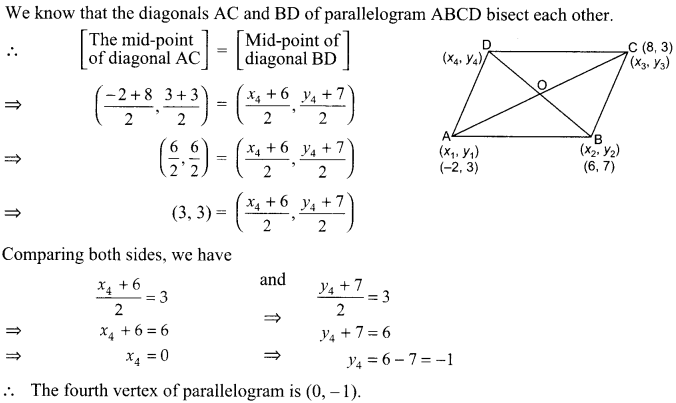
Question 22.
In the given figure, AB || DE and BD || EF. Prove that DC² = CF x AC.
Solution :

Question 23.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution :
Since ABCD is a ||gm
∴ AB = CD and AD = BC
∵  Tangents from an external point to a circle are equal,
∴ AP = AS
BP = BQ RC = QC DR = DS
⇒ (AP + PB) + (RC + DR) = (AS + DS) + (BQ + QC)
⇒ AB + CD = AD + BC
⇒  2 AB = 2 AD ⇒  AB = AD
i.e., ABCD is a rhombus.

Question 24.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution :
Steps:
(i) Draw AB = 7.6 cm.
(ii) Draw ray AX making any suitable angle with AB.
(iii) Draw ray BY parallel to ray AX by making alternate angles BAX and ABY equal.
(iv) Since 5 + 8=13, from AX cut thirteen equal segments AA₁ A₁A₂, A₂A₃, …, a₁₂a₁₃.
(v) Also,from BY cut 13 equal segments (of the same size as taken in step (iv) BB₁, B₁B₂, B₂B₃,…, B₁₂B₁₃.

(vi) Join A₅ with B₈.
Line joining A₅ and B₈ cuts line segment AB at point P
∴ P is the required point such that AP : PB = 5 : 8.
On measuring we find: AP = 2.9 cm and BP = 4.7 cm

Question 25.
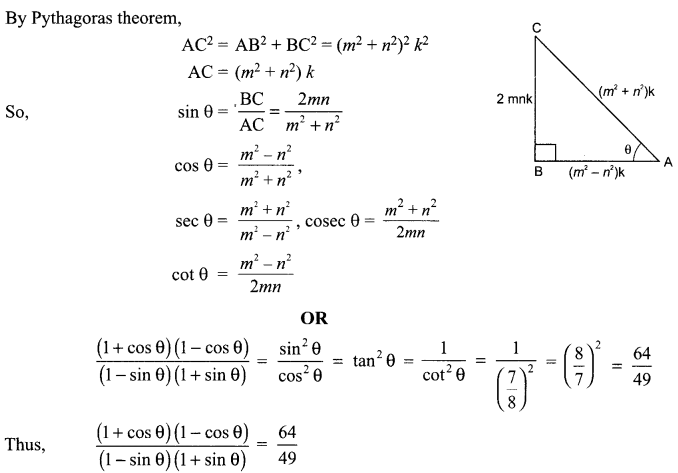
Find the value of other t-ratios if \(\tan \theta=\frac{2 m n}{m^{2}-n^{2}}\)
OR
If \(\cot \theta=\frac{7}{8}\) , then what is the value of \(\frac{(1+\cos \theta)(1-\cos \theta)}{(1-\sin \theta)(1+\sin \theta)}\)
Solution :

Question 26.
Find the sum of the first 51 terms of an AP whose second term is 2 and fourth term is 8. 2
Solution :
Given, a₂= 2 = a + d
and a₄ = 8 = a + 2d
From (i) and (ii),
2 d – 6 ⇒ d = 3
and a = – 1

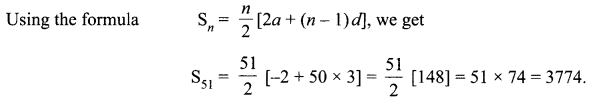
Section – IV 

Question 27.
Prove that \(2 \sqrt{3}-7\) is an irrational.
Solution :

Question 28.
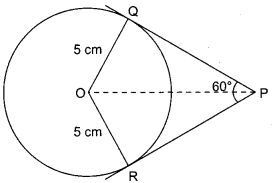
If two tangents inclined at an angle 60° are drawn to a circle of radius 5 cm, then find the length of each tangent.

Solution :

Question 29.
A number consists of two digits, where the number is divided by the sum of its digits, the quotient is 7. If 27 is subtracted from the number, the digits interchange their places, find the number.
Solution :

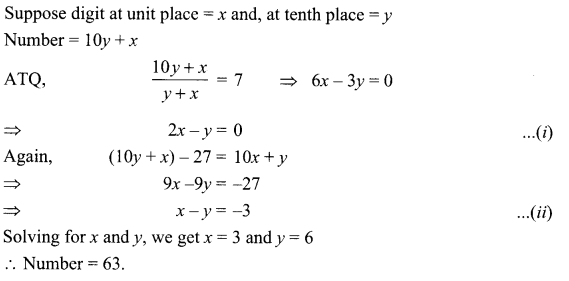
Solving for x and y, we get x = 3 and y = 6
Number = 63.

Question 30.
A school has five houses, A, B, C, D and E. A class has 23 students, 4 from house A, 8 from house B, 5 from house C, 2 from house D and rest from house E. A single student is selected at random to be the class monitor. Find the probability that the selected student is not from A, B and C.
OR
A card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is:
(i) a jack or a king
(ii) a non-ace
(in) a red card
Solution :
T(E) = 23
F(E) = not from A, B, C i.e. = 23 – (4 + 8 + 5)
F(E)= 23 – 17 = 6
\(P(F)=\frac{6}{23}\)
OR

Question 31.
A circus tent is cylindrical to a height of 3 m and conical above it. If its base radius is 52.5 m and slant height of the conical portion is 53 m, find the area of the canvas needed to make the tent.                                                                          Solution :
For cylindrical part:
We have, radius (r) = 52.5 m
Curved Surface area = 2πrh

For the conical part:
Slant height (l) = 53 m
Radius (r) = 52.5 m
Curved surface area = nπl
Area of the canvas = 2nπh + πrl = πr (2h + l)

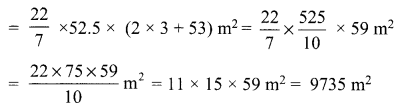
Question 32.
Prove that: tan² A – tan² B =\(\frac{\sin ^{2} A-\sin ^{2} B}{\cos ^{2} A \cdot \cos ^{2} B}\)
Solution :

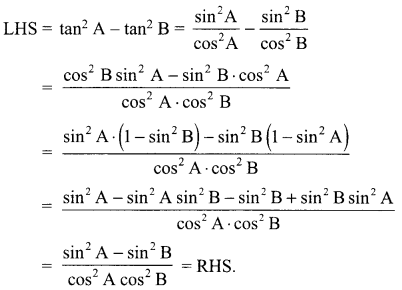
Question 33.
Find two numbers whose sum is 27 and product is 182.
OR
The two numbers differ by 2 and their product is 360. Find the numbers.
Solution :
Here, sum of the numbers is 27.
Let one of the numbers be x.
∴ Other number = 21 -x According to the condition,
Product of the numbers = 182 ⇒
⇒  x (27 – x) = 182
⇒ 27x – x² = 182
⇒ -x² + 27x – 182 = 0
⇒ x² – 27x+ 182 = 0
⇒ x² – 13x – 14x + 182 = 0 ∵ – 27 = (- 13) + (- 14) and (- 13) x (- 14)= 182
⇒ x(x- 13)- 14 (x- 13)= 0
Either x – 13 = 0 ⇒ x = 13
or x – 14 = 0 ⇒ x = 14
when first number is 13, then other number = 27-13 = 14
and when first number is 14 then other number is 27 – 14 = 13.
Thus, the required numbers are 13 and 14.
OR
Let the two numbers be x and x + 2 According to the questions,
x(x + 2) = 360
⇒ x² + 2x = 360 ⇒ x² + 2x – 360 = 0
Splitting the middle term, we get
x² + 20x -18x – 360 = 0 ⇒ x(x + 20) – 18(x + 20) = 0
⇒(x + 20)(x — 18) = 0 ⇒ x = -20 or x = 18
When x = -20, x + 2 = -20 + 2 = -18
When x = 18,x + 2 = 18 + 2 = 20
Hence, the required numbers are -20, -18 or 18, 20.

Section-V

Question 34.
A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 Find the height of the tree.
OR
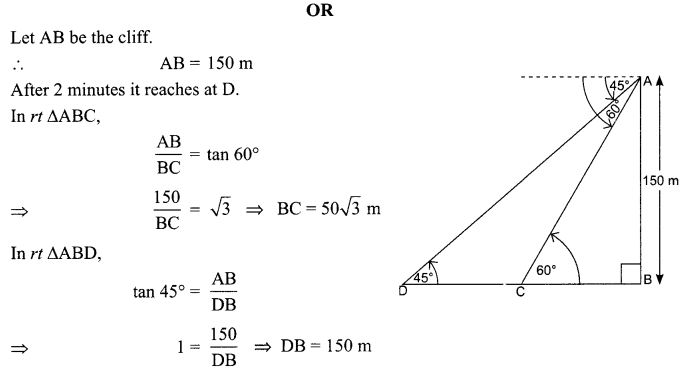
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/min.
Solution :

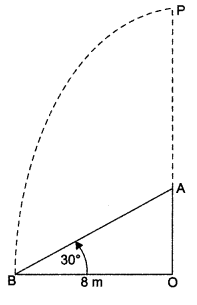
Let the original height of the tree = OP.
It is broken at A and its top is touching the ground at B.
Now, in right Δ AOB, we have

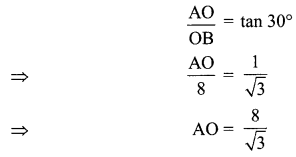
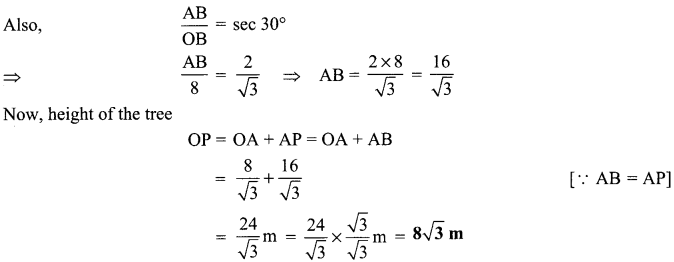
Question 35.
If the sum of first 7 terms of an A.P. is 49 and that of first 17 terms is 289, find the sum of n
Solution :
Let the first term = a and the common difference = d.
Using  \(S_{n}=\frac{n}{2}[2 a+(n-1) d]\)

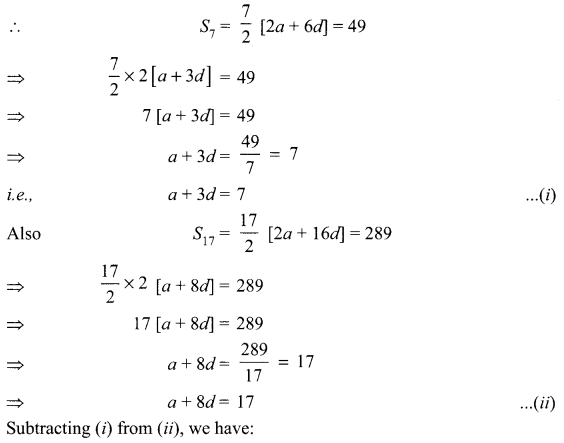
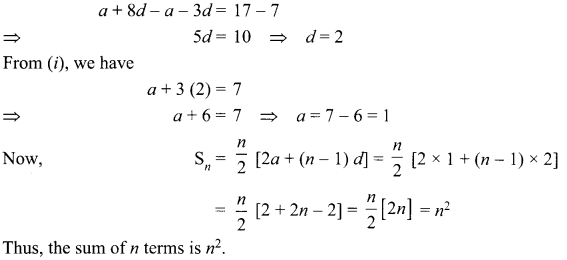
Question 36.
The mean of the following frequency distribution is 57.6. and the number of observations is 50. Find the missing frequencies f₁ and f₂.

Class	0-20	20-40	40-60	60-80	80-100	100-120
Frequency	7	f1	12	f2	8	5

Solution :