CBSE Sample Papers for Class 10 Maths Basic Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 2 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.

Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.

Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.

Part – A
Section-I

Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.

Question 1.
Express 156 as the product of primes.
Solution :
156 = 2² × 3 × 13

Question 2.
Write a quadratic polynomial, sum of whose zeroes is 2 and product is -8.
Solution :
Quadratic polynomial is given by x² – (α + β)x + αβ = x² – 2x – 8

Question 3.
Given that HCF (96, 404) is 4, find the LCM ( 96, 404).
OR
State the fundamental Theorem of Arithmetic.
Solution :
\(\mathrm{LCM}(96,404)=\frac{96 \times 404}{\mathrm{HCF}(96,404)}=\frac{96 \times 404}{4}=9696\)
OR
Every composite number can be expressed (factorized) as a product of primes, factorization is unique, apart from the order in which the factors occur.

Question 4.
On comparing the ratios of the coefficients, find out whether the pair of equations x-2y = 0 and 3x + 4y – 20 = 0 is consistent or inconsistent.
Solution :
x – 2y = 0
3x + 4y – 20 = 0
\(\frac{1}{3} \neq \frac{-2}{4}\)
As, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) is one condition for consistency.
Therefore, the pair of equations is consistent.

Question 5.
If a and b are co-prime numbers, then find the HCF (a, b).
Solution :
1

Question 6.
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°. (Take π = 22/7).
OR
A horse is tied to a pole with 28 m long rope. Find the perimeter of the field where the horse can graze.
(Take π = 22/7)
Solution :

Question 7.
In the given fig. DE || BC, ∠ADE = 70° and ∠BAC = 50°, then angle ∠BCA = ……..

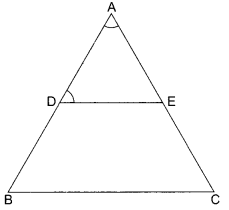
OR
In the given figure, AD = 2 cm, BD = 3 cm, AE = 3.5 cm and AC = 7 cm. Is DE parallel to BC?

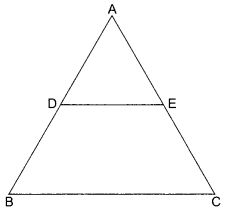
Solution :

Question 8.
The cost of fencing a circular field at the rate of ₹ 24 per metre is ₹ 5280. Find the radius of the field.
Solution :

Question 9.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground where it makes an angle 30°. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree from where it is broken.
Solution :

Question 10.
If the perimeter and the area of a circle are numerically equal, then find the radius of the circle.
Solution :
Perimeter of circle = Area of circle
⇒ 2nr = nr²
⇒ r = 2 units

Question 11.
Write the empirical relationship among mean, median and mode.
Solution :
3 median = mode + 2 mean

Question 12.
To divide a line segment BC internally in the ratio 3 : 5, we draw a ray BX such that ZCBX is an acute angle. What will be the minimum number of points to be located at equal distances, on ray BX?
Solution :
8

Question 13.
For what values of p does the pair of equations 4x + py +8 =0 and 2x +2y +2 =0 has unique solution?
OR
What type of straight lines will be represented by the system of equations 2x + 3y = 5 and 4x + 6y = 7?
Solution :
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)  is the condition for the given pair of equations to have a unique solution.
\(\Rightarrow \frac{4}{2} \neq \frac{p}{2}\)
⇒ P ≠ 4
Therefore, for all real values of p except 4, the given pair of equations will have a unique solution.

Question 14.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is red?
OR
A die is thrown once. What is the probability of getting a prime number?
Solution :
No. of red balls = 3, No. black balls = 5
Total number of balls = 5 + 3 = 8
Probability of red balls \(=\frac{3}{8}\)
OR
Total no. of possible outcomes = 6
There are 3 prime numbers: 2, 3, 5.
So, probability of getting a prime number \(=\frac{3}{6}=\frac{1}{2}\)

Question 15.
A tower stands vertically on the ground. From a point on the ground, which is 15m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.
Solution :

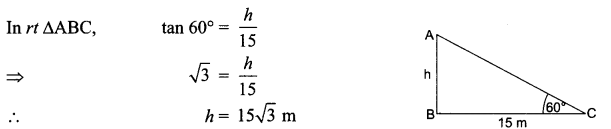
Question 16.
Probability of an event E + probability of the event E (not E) is,
Solution :
1

Section-II

Case study-based questions are compulsory. Attempt any 4 sub-parts from each question. Each sub-part carries 1 mark.

Case Study Based-1

Question 17.

Mathematics teacher of a school took her 10th standard students to show Red fort. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Red fort to students. Then the teacher said in this monument one can find combination of solid figures. There are 2 pillars which are cylindrical in shape. Also 2 domes at the comers which are hemispherical.7 smaller domes are at the centre. Flag hoisting ceremony on Independence Day takes place near these domes.

(i) How much cloth material will be required to cover 2 big domes each of radius 2.5 metres? (Take n = 22/7)
(a) 75 m²
(b) 78.57 m²
(c) 87.47 m²
(d) 25.8 m²

(ii) Write the formula to find the volume of a cylindrical pillar.
(a) nrh
(b) nr!
(c) nr(l + r)
(d) 2nr

(iii) Find the lateral surface area of two pillars if height of the pillar is 7m and radius of the base is 1.4 m. 1
(a) 112.3 cm²
(b) 123.2 m²
(c) 90 m²
(d) 345.2 cm²

(iv) How much is the volume of a hemisphere if the radius of the base is 3.5 m?
(a) 85.9 m³
(b) 80 m³
(c) 98 m³
(d) 89.83 m³

(v) What is the ratio of sum of volumes of two hemispheres of radius 1 cm each to the volume of a sphere of radius 2 cm?
(a) 1 : 1
(b) 1:8
(c) 8 : 1
(d) 1 : 16
Solution :

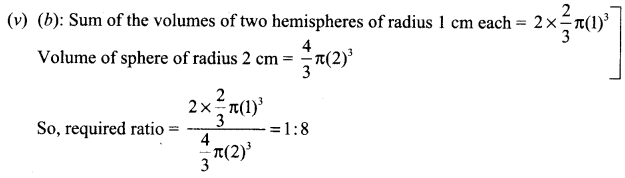
Case Study Based-2

Question 18.
Class X students of a secondary school in Krishnagar have been allotted a rectangular plot of a land for gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of lm from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

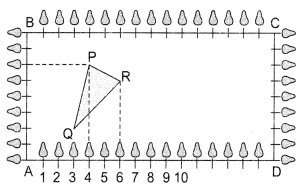
Considering A as origin, answer question (i) to (v).

(i) Considering A as the origin, what are the coordinates of A?
(a) (0,1)
(b) (1,0)
(c) (0,0)
(d) (-1,-1)
Solution :
(c) (0,0)

(ii) What are the coordinates of P?
(a) (4, 6)
(b) (6, 4)
(c) (6,0)
(d) (7,4)
Solution :
(a) (4, 6)

(iii) What are the coordinates of R?
(a) (6, 5)
(b) (5, 6)
(c) (0, 16)
(d) (16, 1)
Solution :
(a) (6, 5)

(iv) What are the coordinates of D?
(a) (12,2)
(b) (-12, 6)
(c) (12, 3)
(d) (6, 10)
Solution :
(a) (12,2)

(v) What are the coordinates of P if D is taken as the origin?
(a) (12,2)
(b) (-12,6)
(c) (12,3)
(d) (6, 10)
Solution :
(b) (-12,6)

Case Study Based-3

Question 19.
Rahul is studying in X Standard. He is making a kite to fly it on a Sunday. Few questions came to his mind while making the kite. Give answers to his questions by looking at the figure.

(i) Rahul tied the sticks at what angles to each other?
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Solution :
(c) 90°

(ii) Which is the correct similarity criteria applicable for smaller triangles at the upper part of this kite?
(a) RHS
(b) SAS
(c)  SSA
(d) AAS
Solution :
(b) SAS

(iii) Sides of two similar triangles are in the ratio 4:9. Corresponding medians of these triangles are in the ratio
(a) 2:3
(b) 4:9
(c) 81:16
(d) 16:81
Solution :
(b) 4:9

(iv) In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle. This theorem is called as,
(a) Pythagoras theorem
(b) Thales theorem
(c) Converse of Thales theorem
(d) Converse of Pythagoras theorem
Solution :
(d) Converse of Pythagoras theorem

(v) What is the area of the kite, formed by two perpendicular sticks of length 6 cm and 8 cm?
(a) 48 cm²
(b) 14 cm³
(c) 24 cm²
(d)  96 cm²
Solition :
(a) 48 cm²

Case Study Based-4

Question 20.
Due to heavy storm, an electric wire got bent as shown in the figure. It followed a mathematical shape. Answer the following questions below:

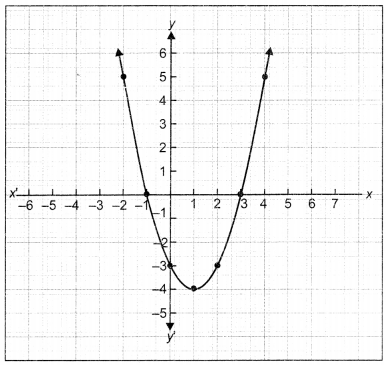
(i) Name the shape in which the wire is bent.
(a) spiral
(b) ellipse
(c) linear
(d) parabola
Solution :
(d) parabola

(ii) How many zeroes are there for the polynomial (shape of the wire).
(a) 2
(b) 3
(c) 1
(d) 0
Solution :
(a) 2

(iii) The zeroes of the polynomial are
(a) -1,5
(b) -1,3
(c) 3,5
(d) -4,2
Solution :
(b) -1,3

(iv) What will be the expression of the polynomial?
(a) x² + 2x – 3
(b) x² – 2x + 3
(c) x² – 2x – 3
(d) x² + 2x + 3
Solution :
(c) x² – 2x – 3

(v) What is the value of the polynomial if x =-1?
(a) 6
(b) -18
(c) 18
(d) 0
Solution :
(d) 0

Part-B
Section-III

All questions are compulsory. In case of internal choices, attempt anyone.

Question 21.
Find the coordinates of the point which divides the line segment joining the points (4, -3) and (8, 5) in the ratio 3 : 1 internally.
OR
Find a relation between x andy such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Solution :

OR
Let P(x,y) be equidistant from the points A(7, 1) and B(3, 5)
Give AP = BP. So. AP² = BP²
(x—7)²+(y— 1)2= (x—3)2+(v—5)2
x² — 14x+49+y²—2y+ I = x²—6x+9+y²— 10y+25
x – y= 2

Question 22.
In the fig. if LM || CB and LN || CD, prove that \(\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{ND}}\)

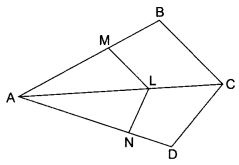
Solution :

Question 23.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.

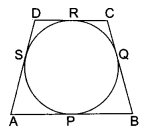
Solution :
To prove: AB + CD = AD + BC
Proof: AS = AP (Length of tangents from an external point to a circle are equal)
BQ= BP
CQ = CR
DS = DR
AS + BQ + CQ + DS = AP + BP + CR + DR
(AS + DS) + (BQ + CQ) = (AP + BP) + (CR + DR)
AD + BC = AB + CD

Question 24.
Draw a line segment of length 7.8 cm and divide it in the ratio 5:8. Measure the two parts.
Solution :

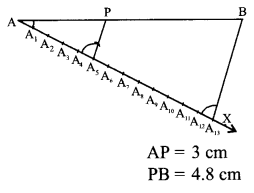
Question 25.
Given 15 cot A = 8, find sin A and sec A.
OR
Find tan P – cot R

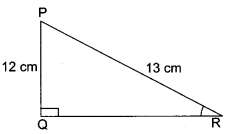
Solution :

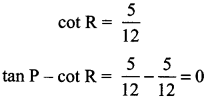
Question 26.
How many terms of the A.P: 9, 17, 25……… must be taken to give a supi 636?
Solution :

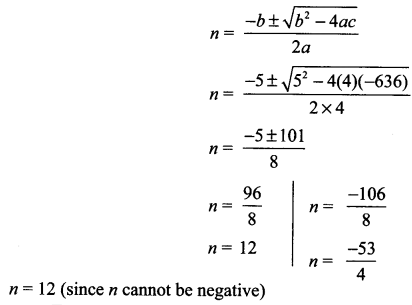
Section-IV

Question 27.
Prove that -√3 is an irrational number.
Solution :

3 divides p² ⇒ 3 divides p
3 is a factor of p
Take p = 3c
3q² = (3c)²
3q² = 9c²    ⇒   q² = 3c²
3 divides g² ⇒ 3 divides q
3 is a factor of 9
Therefore 3 is a common factor of p and q.
It is a contradiction to our assumption that \(\frac{p}{q}\) is rational.
Hence √3 is an irrational number.

Question 28.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.

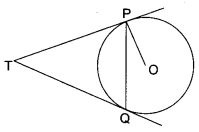
Solution :

Question 29.
Meena went to a bank to withdraw ₹ 2,000. She asked the cashier to give her ₹ 50 and ₹  100 notes only. Meena got 25 notes in all. Find how many notes of ₹ 50 and ₹ 100 she received.
Solution :

Question 30.
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
(i) a two-digit number
(ii) a perfect square number.
(iii) a number divisible by 5. 3
OR
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting (/’) A king of red colour.
(ii) A spade
(iii) The queen of diamond
Solution :
(i) 10,11,12,…, 90 are two digit numbers. Thereare81 numbers. So, probability of getting a two-digit number =
\(=\frac{81}{90}=\frac{9}{10}\)

(ii) 1, 4, 9, 16, 25, 36, 49, 64, 81 are perfect squares. So, probability of getting a perfect square number \(=\frac{9}{90}=\frac{1}{10}\)

(iii) 5, 10, 15,…, 90 are divisible by 5. There are 18 outcomes. So, probability of getting a number divisible by 5.
\(=\frac{18}{90}=\frac{1}{5}\)

OR

(i) Probability of getting “A king of red colour.”
P (King of red colour) \(=\frac{2}{52}=\frac{1}{26}\)

(ii) Probability of getting “A spade”
P (a spade) \(=\frac{13}{52}=\frac{1}{4}\)

(iii) Probability of getting “the queen of diamond” P (the queen of diamond)
P (the queen of diamond) \(=\frac{1}{52}\)

Question 31.
Metallic spheres of radii 6cm, 8cm and 10cm respectively are melted to form a solid sphere. Find the radius of the resulting sphere.
Solution :

Question 32.
\(\text { Prove that } \frac{\sin A-\cos A+1}{\sin A+\cos A-1}=\frac{1}{\sec A-\tan A}\)
Solution :

Question 33.
A motor boat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
OR
Find two consecutive odd positive integers, sum of whose squares is 290.
Solution :
Given: Speed of boat = 18 km/hr,
Distance = 24 km
Let x be the speed of stream.
Let t₁ and t₂ be the time for upstream and downstream. As we know that,



OR
Let one of the odd positive integer be x
then the other odd positive integer is x + 2
ATQ, x² + (x+2)² = 290
⇒  x² + x² + 4x + 4 = 290
⇒ 2 x 2 + 4x – 286 = 0
⇒ 2(x² + 2x – 143) = 0
⇒ x² + 2x – 143 = 0
⇒ x² + 13x — 11x — 143 = 0
⇒ x(x + 13) — 11(x + 13) = 0
⇒ (x – 11)(x + 13) = 0
⇒  (x – 11)0,(x + 13) = 0
Therefore, x = 11 or  -13
According to question, x is a positive odd integer.
Hence, we take positive value of x
So, x = 11 and(x + 2)11 + 2 = 13
Therefore, the odd positive integers are 11 and 13.

Section-V

Question 34.
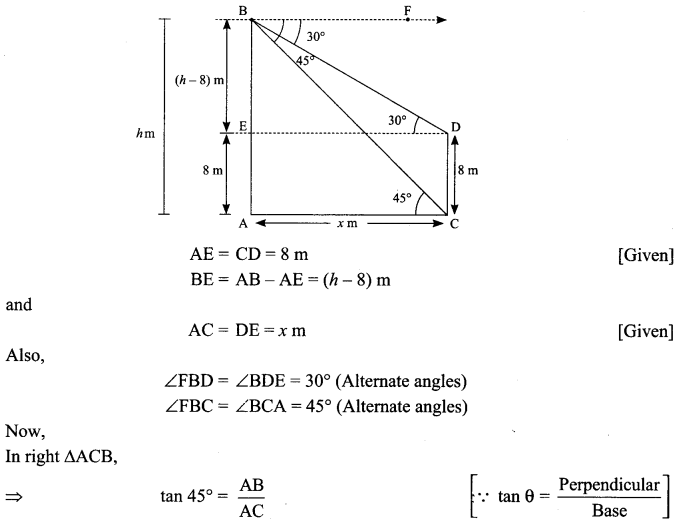
The angles of depression of the top and bottom of a 8m tall building from the top of a multistoried building are 30° and 45°, respectively. Find the height of the multi-storied building and the distance between the two buildings.
OR
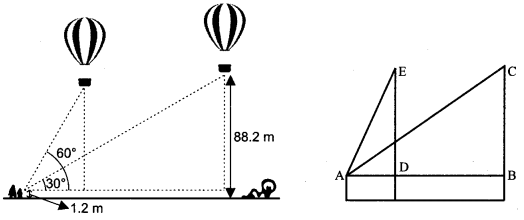
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After sometime, the angle of elevation reduces 30°. Find the distance travelled by the balloon during the interval.

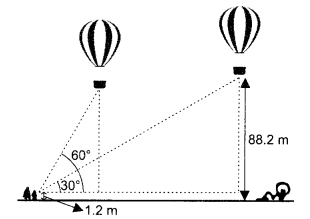
Solution :

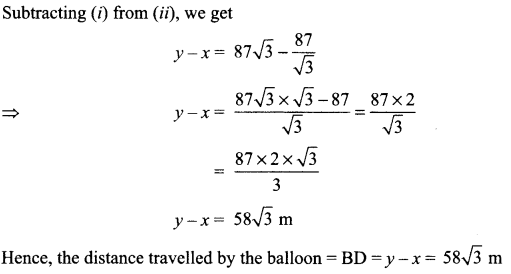
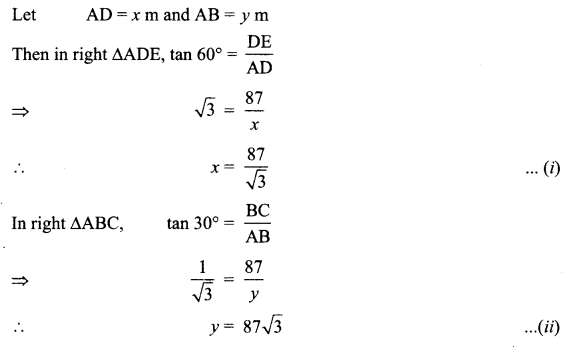
Question 35.
The p^th q^th and r^th terms of an A.P. are a, b and c Show that a(q – r) + b(r -p) + c(p – q) = + c(p – q) = 0                            Solution :
Let AB be the multi-storied building of height hm and CD the building at a distance xm.
Let A be the first term and D the common difference of A.P.
T_p = a = A + (p – 1)D(A – D) + pD …………(i)
T_q= b = A + (q – 1)D = (AD) + qD ……….(ii)
T_r = c = A + (r – 1)D(A – D) + rD ……………(iii)
Here we have got two unknowns A and D which are to be eliminated.
We multiply (i), (ii) and (iii) by q  – r, r  – p and p  – q respectively and add:
a(q – r) = (A – D)(q – r) + Dp(q – r)
b(r – p) (A – D)(r – p) + Dq(r – p)
c(p – q) – (A – D)(p – q) + Dr(p – q)
a(q  – r) + b(r  – p) + c(p – q)
= (A – D)[q – r + r – p + p – q] + D[p(q – r) + q(r – p) + r(p – q)]
= (A – D)(0) + D[pq — pr + qr — pq + rp  – rq)
= 0

Question 36.
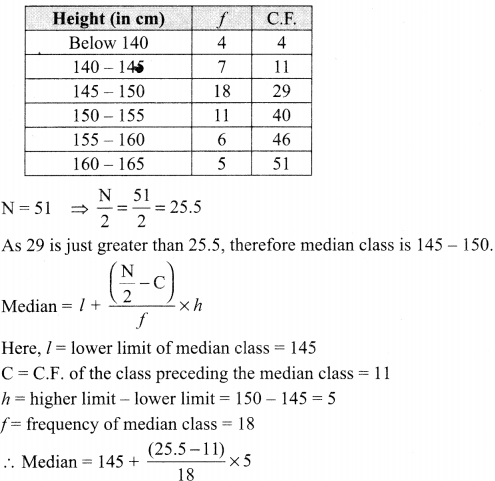
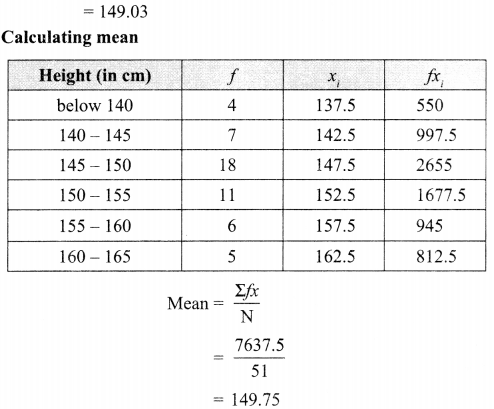
A survey regarding the heights (in cm) of 51 girls of class X of a school was conducted and the following data was obtained. Find the median height and the mean using the formulae.

Height (in cm)	Number of Girls
Less than 140	4
Less than 145	11
Less than 150	29
Less than 155	40
Less than 160	46
Less than 165	51

Solution :