CBSE Sample Papers for Class 10 Maths Basic Set 4 for Practice

Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Set 4 for Practice

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.

Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.

Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.

Part – A
Section-I

Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.

Question 1.
Find the value of k for which the system of equations kx + 4y = k – 4, 16x + ky = k have infinitely many solutions.
Solution :
K = 2

Question 2.
Find the perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0)
Solution :
8

Question 3.
Evaluate: sin 60° cos 30° + sin 30° cos 60°.
OR
Evaluate: 2 tan² 45° + cos² 30° – sin² 60°
Solution :
1 OR 2

Question 4.
Write the Value of \(\frac{1+\tan ^{2} \theta}{1+\cot ^{2} \theta}\)
Solution :
tan² θ

Question 5.
Three solid spheres of diameter 6 cm, 8 cm and 10 cm are melted to form a single solid sphere. Find the diameter of the new sphere?
Solution :
12 Cm

Question 6.
In the given AP, find the missing term: 2,……. , 26.
OR
Which term of the A.P.: 121, 117, 113………… is the first negative terms?
Solution :
14 OR 32

Question 7.
In ΔABC, DE is a line parallel to BC. If AC = 6.4 cm, AE = 4 cm. Find DE

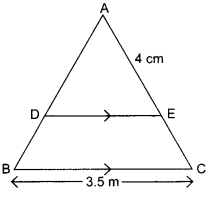
OR
In the given figure, ΔABR ~ ΔPQR. If AR = 45 cm, AP = 72 cm and QR = 48 cm, then find BR

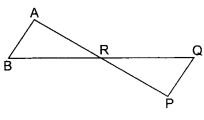
Solution :
2.115 cm OR  27 cm

Question 8.
Find the largest number which divides 70 and 125, leaving remainders 5 and 8 respectively.
Solution :
13

Question 9.
Find the nature of roots for the quadratic equation 2x² – √5x +1 = 0. 1
Solution :
Not real

Question 10.
How many tangents can a circle have?
Solution :
Infinitely many

Question 11.
The graph of y =p(x) are given in figures below, for some polynomials p(x). Find the number of zeroes of p(x).

Solution :
1

Question 12.
If the height of a cone is equal to diameter of its base, find the volume of the cone.
Solution :
\(\frac{2}{3} \pi r^{3}\)

Question 13.
Find the value of x which satifies both the equations 4x -5 =y and 2x-y = 3, when v = -1.
OR
Write whether the following pair of linear equations is consistent or not? x +y = 14, x -y = 4
Solution :
1 OR Consistent

Question 14.
A man goes 12 m due east and then 5 m due north. Find his distance from the start in point.                                              OR
Find the angle of elevation of a point which is at a distance of 30 m from the base of a tower 10√3m high.
Solution :
13 m OR 30°

Question 15.
The mid-point of the line joining A (a, 2) and B(3, 6) is (2, b). Write the numerical values of a and b.
Solution :
a = 4 and b = 1

Question 16.
What is called the line drawn from the eye of an observer to the point in the object viewed by the observer?
Solution :
Line of sight

Section-II

Case Study Based-1

Case study-based questions are compulsory. Attempt any 4 sub-parts from each question. Each sub-part carries 1 mark.

Question 17.
An archery target has three regions formed by three concentric circles as shown in the given figure.

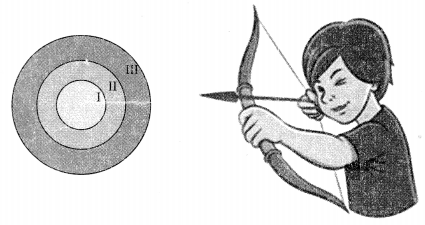
If diameters of three concentric circles are in the ratio 1 : 2 : 3. Answers (i) to (v).

(i) Area of innermost (I) circle is
(a) πr+ 2
(b) πr
(c) m²
(d) 2 πr
Solution :
(c) m²

(ii) Area of region between first (I) and second (II) circle is
(a) 2πr
(b) πr²
(c) 3πr²
(d) 2πr²
Solution :
(c) 3πr²

(iii) Area of region between second (II) and third (III) circles is
(a) 5πr²
(b) 4πr²
(c) 3πr²
(d) 2π²
Solution :
(a) 5πr²

(iv) Ratio of circumferences of three concentric circles are
(a) 2:1:3
(b) 1:2:3
(c) 3:1:2
(d) 3:2:1
Solution :
(b) 1:2:3

(v) Circumference of outermost concentric circle is
(a) 2πr
(b) 2πr
(c) 4πr
(d) 6πr
Solution :
(d) 6πr

Case Study Based-2

Question 18.
In a classroom, 4 friends are seated at the points A, B, C and D as shown is given fig. Rupa and Rupali walk into the class and after observing for a few minutes Rupa asks Rupali, “Don’t you think ABCD is a square? Rupali disagrees. Now answer (i) to (v) to show Rupa is correct.

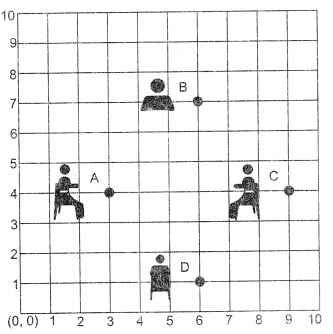
(i) Coordinate of A is …..
(a) (4, 3)
(b) (3,0)
(c) (1,4)
(d) (3,4)
Solution :
(d) (3,4)

(ii) Coordinate of D is…………..
(a) (6, 1)
(b) (1,6)
(c) (2, 6)
(d) (6,2)
Solution :
(a) (6, 1)

(iii) Distance AB is …….
(a) 3+\(\sqrt{2}\)
(b) \(\sqrt{2}\)
(c) 2\(\sqrt{2}\)
(d) 3\(\sqrt{2}\)
Solution :
(d) 3\(\sqrt{2}\)

(iv) Diagonal AC is ………….
(a) 3
(b) 4
(c) 6
(d) 6
Solution :
(c) 6

(v) ABCD is a …………..
(a) rectangle
(b) square
(c) rhombus
(d) trapezium
Solution :
(b) square

Case Study Based-3

Question 19.
Five friends make up their minds to play a game by using a spinner. They put a spinner down on the ground and set around themselves to play. A spimier contains eight regions, numbered through 8, as shown in the figure, the arrow has an equally likely chance of landing on any of the eight regions. If the arrow lands on a line, the result is not…

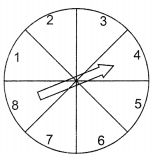
(i) How many possible outcomes are in the sample spaces?
(a) 4
(b) 6
(c) 8
(d) 10
Solution :
(c) 8

(ii) What is the probability that the arrow lands on 4?
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{6}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{8}\)
Solution :
(d) \(\frac{1}{8}\)

(iii) The set of possible outcomes for event A, in which the arrow lands on an even number is …..
(a) 2, 4, 6, 8
(b) 2, 4, 6, 10
(c) 2, 6, 8, 10
(d) 4, 6, 8 10
Solution :
(a) 2, 4, 6, 8

(iv) The probability that the arrow lands on an even number is ………….
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{6}\)
(c)\(\frac{1}{8}\)
(d) \(\frac{1}{2}\)
Solution :
(d) \(\frac{1}{2}\)

(v) The probability that the arrow will point at any factor of 8 is …………
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c)\(\frac{1}{6}\)
(d) \(\frac{1}{8}\)
Solution :
(a) \(\frac{1}{2}\)

Case Study Based-4

Question 20.
A square park has each side of 100 m. At each comer of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in given figure. Answer the question from (i) to (v):

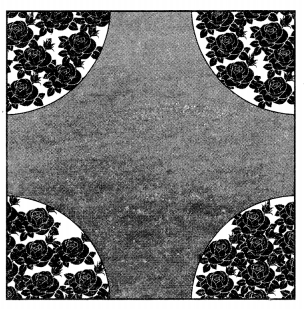
(i) Area of each quadrant is
(a) 145 m²
(b) 154 m²
(c) 415 m²
(d) 514 m²
Solution :
(b) 154 m²

(ii) Area of 4 quadrants is …………
(a) 616 m²
(b) 166 m²
(c) 661 m²
(d) 510m²
Solution :
(a) 616 m²

(iii) Area of park with bed roses is …………
(a) 10,000 m²
(b) 1000 m²
(c) 100 m²
(d) 10 m²
Solution :
(a) 10,000 m²

(iv) Area of park without bed roses is …………
(a) 9834 m²
(b) 9384 m²
(c) 9483 m²
(d) 9348 m²
Solution :
(b) 9384 m²

(v) Angle of a quadrant is equal to …………
(a) 70°
(b) 80°
(c) 90°
(d) 45°
Solution :
(c) 90°

Part-B
Section-III

All questions are compulsory. In case of internal choices, attempt anyone.

Question 21.
Explain why 7 × 11×13 × 15 + 15 is a composite number.
OR
Prove that \(\frac{1}{2-\sqrt{5}}\) is an irrational number.
Solution :
It has more than two factors so it is composite

Question 22.
Find value of P for which the product of roots of the quadratic equation Px² + 6x + 4P = 0 is equal to the sum of the roots.
Solution :
\(P=\frac{-3}{2}\)

Question 23.
In the given figure,∠1 = ∠3, ∠2 = ∠4, DE = 4 units, CE = x + 1, AE = 2x + 4 and BE = 4x – 2. Find x.

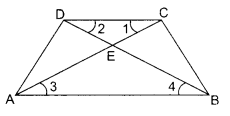
Solution :
x = 3 units

Question 24.
Find a cubic polynomial with the sum, sum of the products of its zeroes taken two at a time,and product of its zeroes at 5, -6, and -20 respectively.
Solution :
x³ – 5x² – 6x

Question 25.
If tan A = √2 -1, show that  \(\frac{\tan A}{1+\tan ^{2} A}=\frac{\sqrt{2}}{4}\)
OR
\(\text { If } \sec \theta=\frac{5}{4}, \text { verify that } \frac{\tan \theta}{1+\tan ^{2} \theta}=\frac{\sin \theta}{\sec \theta}\)

Question 26.
Find the median of the following frequency distribution:

C.I	0-10	10-20	20-30           30-40		40-50	50-60
f	5	3	10	6	4	2

Solution :
27

Section-IV

Question 27.
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of the line segment PQ.

Question 28.
Show graphically that the system of equations x + 2y = 5; 3x + 6y = 15 have infinitely many solutions.

Question 29.
Prove that 3 √3 is an irrational number.

Question 30.
From the top of a tower 50 m high, the angle of depression of the top of a pole is 45° and from the foot of the pole, the angle of elevation of the top of the tower is 60°. Find the height of the pole if the pole and tower stand on the same plane.
OR
Two ships are there in the sea on either side of a lighthouse in such a way that the ships and the lighthouse are in the same straight line. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45°. If the height of the lighthouse is 200 m, find the distance between the two ships.
Solution :
21.16m OR 315.33 m

Question 31.
If \(\tan \theta=\frac{4}{3}\) ,find the value of  \(\frac{3 \sin \theta+2 \cos \theta}{3 \sin \theta-2 \cos \theta}\)
Solution :
3

Question 32.
If x = \(\frac{2}{3}\) and x = -3 are roots of the quadratic equations ax² + 7x + b = 0, find the values of a and b.
Solution :
a = 3,b = – 3

Question 33.
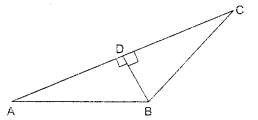
In the given figure, ABC is a triangle and BD ⊥ AC. Prove that AB² + CD² = AD² + BC².

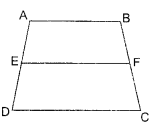
ABCD is a trapezium with AB || DC. E and F are points on non¬parallel sides AD and BC respectively such that EF is parallel to AB (see figure).Show that \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BF}}{\mathrm{FC}}\)

Section-V

Question 34.
The first and the last term of an AP are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum?
OR
In an AP the first term is 8 and n^th term is 33 and sum to first n terms is 123. Find n and d, the common difference.
Solution :
n= 39, S_n =6981
5 n OR n = 6, d = 5 36

Question 35.
Draw a circle of radius 4 cm. From a point P, 9 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents.

Question 36.
Take mean of the following distribution is 50. Find the value of x

Class interval	0-20	20-40	40-60	60-80	80-100
Frequency	34	3x – 4	64	48	2(x-1)

Solution :
x = 20