tudents can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 5 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Basic Set 5 for Practice
Time: 3 Hours
Maximum Marks: 80
General Instructions:
1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.
Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Section-I
Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
Question 1.
Find the common solution of ax + by = c and y-axis.
Solution :
\(\left(0, \frac{c}{b}\right)\)
Question 2.
If P\(\mathrm{P}\left(\frac{a}{3}, 4\right)\) is the mid-point of the line segment joining the points
Q(-6, 5) and R(-2, 3), then what is the value of a?
Solution :
a = – 2
Question 3.
In the given AP, find the missing terms:……….
OR
What will be the value of a8 – a4 for the following A.P. 9, 14 ………. 254
Solution :
18 , 8 OR 20
Question 4.
Find the value of \(\frac{\sin \theta}{\sqrt{1-\sin ^{2} \theta}}\)
Solution :
tan θ
Question 5.
Find the value of k for which the given system has unique solution. 2x + 3y – 5 = 0, kx-6y- 8 = 0
Solution :
k ≠ -4
Question 6.
If \(\sec \theta=\frac{25}{7}\) then find tan θ
OR
If \(\cos \theta=\frac{3}{5}, \text { then find } \frac{\sin \theta-\cot \theta}{2 \tan \theta}\)
Solution :
\(\frac{24}{7} \text { OR } \frac{3}{160}\)
Question 7.
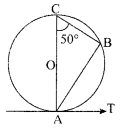
In the given figure, AB is a chord of the circle and ∠ACB = 50°. If AT is the tangent to the circle at the point A, then find the value of ∠BAT.
To divide a line segment AB in the ratio 4 : 5, first a ray AX is drawn making ∠BAX an acute angle and then points A1 A2, A3,… at equal distances are marked on the ray AX. At what point is point B joined?
Solution :
50° OR A9
Question 8.
Write a rational number between \(\sqrt{2} \text { and } \sqrt{3}\) ?
Solution :
1.666………..
Question 9.
Find the roots of quadratic equation x2 – 7 x = 0.
Solution :
0,7
Question 10.
If one zero of the quadratic polynomial x2 – 5x – 6 is 6, then find its other zero.
Solution :
-1
Question 11.
If xi are the mid-points of the class intervals of grouped data, fi are the corresponding frequencies and \(\bar{x}\) is the mean, then find the value of \(\Sigma\left(f_{i} x_{i}-\bar{x}\right)\)
Solution :
0
Question 12.
Find the arithmetic mean of 1, 2, 3,…. n
Solution :
\(\frac{n+1}{2}\)
Question 13.
Two dice are thrown simultaneously. Find the probability of obtaining a total score of 5?
OR
A die is thrown once. What is the probability of getting a number greater than 4?
Solution :
\(\frac{1}{9} \text { OR } \frac{1}{3}\)
Question 14.
Find the class mark of classes 10-25 and 35-55.
OR
Find the value of x, if the mode of the following data is 25.
15, 20, 25, 18, 14, 15, 25, 15, 18, 16, 20, 25, 20, x, 18
Solution :
17.5,45 OR 25
Question 15.
Find the value of p if the lines represented by the equations 3x – y – 5 = 0 and 6x – 2y -p = 0 are parallel.
Solution :
All real valuex of ‘p’ except ’10’
Question 16.
In ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm, then find ∠B
Solution :
90°
Section-II
Case Study Based-1
Case study-based questions are compulsory. Attempt any 4 sub-parts from each question. Each sub-part carries 1 mark.
Question 17.
A boy goes to the market v/ith his mom. He sees a toy and wants to buy it. This toy is in the form of a cone mounted on a hemisphere of common base of radius 7 cm. The total height of the toy is 31 cm. Now answer questions (I) to (v).
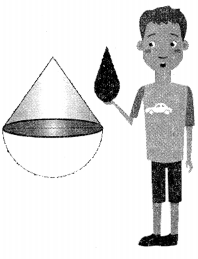
(i) What is the curved surface area of hemisphere?
(a) 309 cm2
(b) 308 cm2
(c) 803 cm 2
(d) 903 cm2
Solution :
(b) 308 cm2
(ii) Write the formula to find curved surface area of cone?
(a) πrl
(b) πl
(c) πr(l + r)
(d) 2πr
Solution :
(a) πrl
(iii) Slant height of a cone is ………
(a) 26 cm
(b) 25 cm
(c) 52 cm
(d) 62 cm
Solution :
(b) 25 cm
(iv) What is the curved surface area of cone?
(a) 505 cm2
(b) 55 cm2
(c) 550 cm2
(d) 555 cm2
Solution :
(c) 550 cm2
(v) Find the total surface area of the toy.
(a) 858 cm2
(b)885 cm2
(c) 588 cm2
(d) 855 cm2
Solution :
(a) 858 cm2
Case Study Based-2
Question 18.
To conduct sports day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in figure given below. Niharika runs \(\frac{1}{4} \text { th }\) the distance AD on the 2nd line and posts a green flag. Preet runs \(\frac{1}{5} \mathrm{th}\) the distance.
AD on the eighth line and posts a red flag.
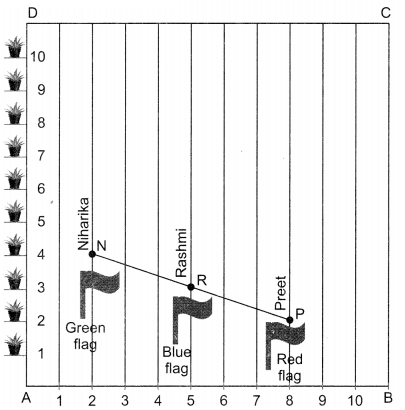
Answer questions (i) to (v)
(i) Write the coordinates of point N.
(a) (1,25)
(b) (2,25)
(c) (4, 25)
(d) (3,25)
Solution :
(b) (2,25)
(ii) Write the coordinates of point P.
(a) (2, 80)
(b) (8,2)
(c) (8,20)
(d) (2, 8)
Solution :
(c) (8,20)
(iii) What is the distance between green and red flags?
(a) \(\sqrt{63} \mathrm{~m}\)
(b) \(\sqrt{26} \mathrm{~m}\)
(c) \(\sqrt{62} \mathrm{~m}\)
(d) \(\sqrt{61} \mathrm{~m}\)
Solution :
(d) \(\sqrt{61} \mathrm{~m}\)
(iv) What is the coordinates of R?
(a) (5,22)
(b) (5,22.5)
(c) (22.5, 5)
(d) (22,5)
Solution :
(b) (5,22.5)
(v) Distance between Niharika and Rashmi is ……….
(a) 3.90 m
(b) 4.01 m
(c) 3.06 m
(d) 5.10 m
Solution :
(a) 3.90 m
Case Study Based-3
Question 19.
Some students of class-Xth get together and decide to form a design by combining different mathematical shapes. First of all they select a triangle ABC with AB = 3 cm, AC = 4 cm and ∠B AC = 90°. They draw semicircles on sides AB, AC and BC but they have some doubts which they want to clarify with you. So, answer their questions given below:
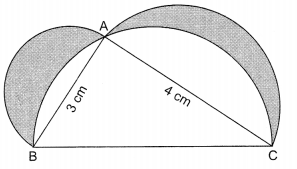
(i) The length of side BC is ………
(a) 5 cm
(b) 25 cm
(c) 9 cm
(d) 16 cm
Solution :
(a) 5 cm
(ii) Area of semicircle on side AB is ……….
(a) \(\frac{3}{2} \pi \mathrm{cm}^{2}\)
(b) \(\frac{9}{8} \pi \mathrm{cm}^{2}\)
(c) 9 π cm2
(d) 4 π cm2
Solution :
(b) \(\frac{9}{8} \pi \mathrm{cm}^{2}\)
(iii) Area of semicircle on side AC is ……..
(a) 4 π cm2
(b) 2 π cm2
(c) 9 π cm2
(d) 16 π cm2
Solution :
(b) 2 π cm2
(iv) Area of given figure is ………
(a) \(\left(\frac{9}{4} \pi+6\right) \mathrm{cm}^{2}\)
(b) \(\left(\frac{16 \pi}{9}+6\right) \mathrm{cm}^{2}\)
(c) \(\left(\frac{25 \pi}{8}+6\right) \mathrm{cm}^{2}\)
(d) \(\left(\frac{4 \pi}{25}+6\right) \mathrm{cm}^{2}\)
Solution :
(c) \(\left(\frac{25 \pi}{8}+6\right) \mathrm{cm}^{2}\)
(v) Find the area of the shaded region.
(a) 6 cm2
(b) 8 cm2
(c) 10 cm2
(d) 12 cm2
Solution :
(a) 6 cm2
Case Study Based-4
Question 20.
A human chain is to be formed in concentric form of radius 56 m and 63 m at India Gate. But the organiser has some problems, he wants you to solve his problems. Give answer to his questions by using information given in the question :

(i) The circumference of circular chain of radius 56 m is
(a) 352 m
(b) 176 m
(c) 704 m
(d) 88 m
Solution :
(a) 352 m
(ii) The area covered by circular chain of radius 56 m is
(a) 5544 m2
(b) 3850 m2
(c) 9856 m2
(d) 12474 m2
Solution :
(c) 9856 m2
(iii) If each person is given two metres of space to stand, find how many persons can be accomodated in the chain of radius 56 m.
(a) 126 persons
(b) 176 persons
(c) 156 persons
(d) 186 persons
Solution :
(b) 176 persons
(iv) He wants to include one more concentric circle with a radius of 63 m, the circumference of the new circle will be
(a) 156 m
(b) 396 m
(c) 176 m
(d) 288 m
Solution :
(b) 396 m
(v) How many more persons can he accomodate on the new circle:
(a) 198 persons
(b) 156 persons
(c) 176 persons
(d) 186 persons
Solution :
(a) 198 persons
Part-B
Section-III
All questions are compulsory. In case of internal choices, attempt anyone.
Question 21.
Find the median of the following distribution:
| X | 10 | 12 | 14 | 16 | 18 | 20 |
| fi | 3 | 5 | 6 | 4 | 4 | 3 |
If the mean of the following distribution is 54, find the value of P.
| Class | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| Frequency | 7 | P | 10 | 9 | 13 |
Solution :
14.8 OR 11
Question 22.
State fundamental theorem of Arithmetic and hence find the unique factorization of 120.
Solution :
2 x 2 x 2 x 3 x 5
Question 23.
In the given figure ∠M = ∠N = 46°, express x in terms of a, b and c, where a, b and c are lengths of LM, MN and NK respectively.
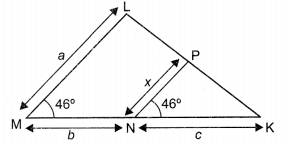
Solution :
\(x=\frac{a c}{b+c}\)
Question 24.
If \(x=\frac{2}{3}\) and x = – 3 are roots of the quadratic equation ax2 + 7x + b = O. Find the value of a and b.
Solution :
a = 3,b = -6
Question 25.
If A = 30°, verity that tan 2A \(=\frac{2 \tan A}{1-\tan ^{2} A}\)
OR
Prove that: tan2 30° + tan2 45° + tan2 60° = \(\frac{13}{3}\)
Question 26.
1000 tickets of a lottery were sold and there are 5 prizes on these tickets. If John has purchased one lottery ticket, what is the probability of winning a prize?
Solution :
\(\frac{1}{200}\)
Section – IV
Question 27.
Prove that 5 – 2/3 is irrational.
Question 28.
In the given figure, AB || DE and BD || EF. Prove that DC2 = CF x AC.
Question 29.
In the given figure, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.
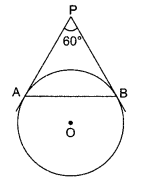
Solution :
5cm
Question 30.
The eighth term of an AP is half its second term and the eleventh term exceeds one-third of its fourth term by 1. Find the 15th term. OR
The sum of three numbers of an AP is 27 and their product is 405. Find the numbers.
Solution :
3 OR 3,9,15 or 15,9,3
Question 31.
If a tower is 30 m height, casts a shadow 10√3 along on the ground. Find the angle of elevation of the Sun.
Solution :
60°
Question 32.
Check whether the pair of equations 3x +y – 2 = 0, 2x – 3y – 5 = 0 is consistent. If so, solve them graphically.
Solution :
Consistent, X= 1,y = -1
Question 33.
Draw a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°. OR
Draw a line segment of length 8 cm and divide it in the ratio 2:3.
Solution :
OR 7cm
Section-V
Question 34.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° Find the height of the tower and the distance of the point from base of the tower. [Take √3 = 1.732]
OR
A tree breaks down due to storm and the broken part bends, so that the top of the tree touches the ground making an angle of 30° with it. The distance from the foot of the tree to the point where the top touches the ground is 8 metres. Find the height of the tree before it was broken.
Solution :
2.5m, 4.33m OR 13.86
Question 35.
The roots a and P of the quadratic equation x2 – 5x + 3(k – 1) = 0 are such that a – p = 11. Find k.
Solution :
K=-7
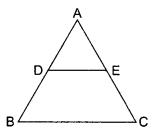
Question 36.
In the given figure, ABC is a triangle in which AB = AC, D and E are points on the sides AB and AC respectively, such that AD = AE. Show that the points B, C, E and D are concylic.