CBSE Sample Papers for Class 10 Maths Basic Term 2 Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths BasicTerm 2 Set 2 with Solutions

Time allowed: 2 hours
Maximum Marks: 40

General Instructions:

• The question paper consists of 14 questions divided into 3 sections A, B, C.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one questions.
• Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one questions. It contains two case study based questions.

Section – A (12 marks)

Question 1.
Solve the quadratic equation p²x² + (p² – q²) x – q² = 0, using quadratic formula.
OR
If α and β are the roots of a quadratic equation and α + β = 4 and α³ + β³ = 47, then form a quadratic equation in terms of x, having roots as α and β. (2)
Answer:
Given, p²x² + (p² – q²) x – q² = 0
On comparing it with standard equation We get
a = p², b = p² – q², c = – q²
∴ D = b² – 4ac
= (P² – q²)² – 4 × p² × (- q²)
= p⁴ – q⁴ – 2p²q² + 4p²q²
= p⁴ + q⁴ + 2 p²q²
= (p² + q²)² > 0
So, the equation has real roots,

Hence, roots are \(\frac{q^{2}}{p^{2}}\) and – 1

Related Theory
This quadratic formula was given by Indian mathematician Sri Dharacharaya. Then for quadratic equation ax² + bx + c = 0, its roots are
\(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
OR
Here, α + β = 4 and
α³ + β³ = 44
⇒ (α + β)³ – 3 αβ(α + β) = 44
⇒ 4³ – 3 αβ (4) = 44
⇒ – 12αβ = 44 – 64
⇒ αβ = \(\frac{20}{12}\) = \(\frac{5}{3}\)
∴ Quadratic equation is:
x² – (α + β)x + αβ = 0
⇒ x² – 4x + \(\frac{5}{3}\) = 0
⇒ 3x² – 12x + 5 = 0, which is the required equation.

Related Theory:
If α and β are the roots of the quadratic equation, then quadratic equation can be formed as:
x² – (α + β)x + αβ = 0

Question 2.
In two APs, 60, 62, 64…. and – 10, – 3, 4, 11, for what value of n are terms equal ? (2)
Answer:
1^st A.P. is 60, 62, 64 …….
Here. a = 60,
d = 62 – 60 = 2
nth term of 1^st A.P. = a + (n – 1 )d
= 60 + (n – 1)2
= 58 + 2n ……. (i)
Terms of 2nd A.P. is – 10, – 3, 4, 11 ……..
Here, a = – 10,
d = – 3 + 10 = 7
∴ n^th term of 2^nd A.P. = a + (n – l)d
= – 10 + (n – 1)7
= – 17 + 7n …… (ii)
From (i) and (ii), we get
58 + 2n = – 17 + 7n
⇒ – 5n = – 75
⇒ n = \(\frac{75}{5}\) = 15
∴ 15th term of both A.P.s are equal.

Caution:
Equate the nth term of both the A.P. to the value of n.

Question 3.
The heights of students in a class are arranged in the tabular from. But some water drops get spilled on it, due to which few enteries got erased.
So, in the given distribution find the value of a, b, c, d. (2)

Height (in cm)	Frequency	Cumulative frequency
150-155	5	12
155-160	a	25
160-165	10	b
165-170	C	43
170-175	5	48
175-180	2	d

Answer:
From the table
12 + a = 25 ⇒ a = 25 – 12 = 13
25 + 10 = b ⇒ b = 35
b + c = 43
⇒ c = 43 – b
= 43 – 35 = 8
48 + 2 = d
⇒ d = 50

Related Theory:
The cumulative frequency can be calculated by adding the frequency of that class to the previous class and the c.f. of last class is equal to sum of all the frequency

Question 4.
Evaluate the sum of all natural numbers less than 100 which are divisible by 6.
OR
Show that the sequence defined as a_n = 2n² + 1 is not an A.P. (2)
Answer:
Natural numbers less than 100 and divisible by 6 are 6, 12, 18, ……….. 96,
a = 6,
d = 6,
and a_n = 96
∴ a + (n – 1)d = 96
6 + (n – 1)6 = 96
⇒ n – 1 = \(\frac{90}{6}\)
⇒ n – 1 = 15
⇒ n = 16 n.
∴ Sum = \(\frac{n}{2}\)[a + a_n]
= \(\frac{16}{2}\)[6 + 96]
= 8 × 102
= 816

Caution:
Use the appropriate formula, for calculating the sum, as number of terms in this A.P. is unknown.
OR
We have, a_n = 2n² + 1
Replacing n by (n + 1) in a_n, we obtain
a_{n + 1} = 2(n + 1)² + 1
= 2n² + 4n + 3
Now, a_{n + 1} – a_n = (2n² + 4n + 3) – (2n² + 1)
= 4n + 2
Clearly, a_{n + 1} – a_n is not independent of n and therefore not constant.
So, the given sequence is not an A.P.

Related Theory:
The common difference is the value between each successive number in an arithmetic sequence. Therefore, the formula for finding the common difference of an A.P. is d = a_n – a_{n – 1}, where an is the last term is the sequence and a_{n – 1} is the previous

Question 5.
The mean of the following data is 14 Then what is the value of k. (2)

X	frequency
5	7
10	k
15	8
20	4
25	5

Answer:
Table for the given data is:

xi	fi	xifi
5	7	35
10	k	10k
15	8	120
20	4	80
25	5	125
Total	Σfi = k + 24	Σ xifi = 10 k + 360

Here, Mean = 14
Mean = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
⇒ 14 = \(\frac{10 k+360}{k+24}\)
⇒ 14(k + 24 )= 10k + 360
⇒ 14k + 336 = 10k + 360
⇒ 14k – 10k = 360 – 336
⇒ 4k = 24
⇒ k = 6
Hence, the value of k is 6.

Question 6.
A solid wooden toy is in the shape of a right circular cone mounted on a hemisphere of radius 4.2 cm. The total height of the toy is 10.2 cm. What is the volume of the toy? [use π = \(\frac{22}{7}\)] (2)
Answer:
From the figure, we have radius of the base of the cone = 4.2 cm and height = 10.2 – 4.2 = 6 cm

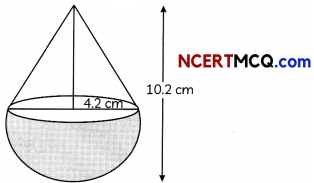
So, volume of the toy = Volume of cone + Volume of hemisphere
= \(\frac{1}{3}\)π(4.2)²6 + \(\frac{2}{3}\)π(4.2)³
= 776.16 + 155.232
= 931.392 cm³

Section – B (12 marks)

Question 7.
Draw a circle of radius 2.2 cm. Take a point P on the circle. From the point P, construct a tangent to the circle.
OR
Draw a line segment of length 6.4 cm. Divide AB in the ratio of 3 : 5. Measure the two parts. (3)
Answer:

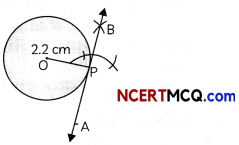
Steps of construction:

1. Draw a circle of radius 2.2 cm with centre O.
2. Draw a circle of radius 2.2 cm, intersecting circle at P.
3. From P, draw a perpendicular.
4. Extend BP.
   Now, BPA is the required tangent.

Related Theory:
Tangent to a circle is always perpendicular to the radius.
OR

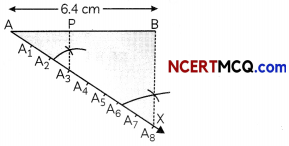
Steps of construction:

• Draw a line segment of length 6.4 cm.
• Draw an acute angle ZBAX.
• Make eight equal marks on ray AX.
• Join A8B.
• Draw a line from A3 parallel to A8B.
• P is the required point of intersection on AB

Here, P divide AB in the ratio of 3 : 5
∴ AP = 3.9 cm
PB = 2.5 cm

Caution:
The number of divisions, in which acute angle line is to be divided is the sum of the ratios i.e. 3 + 5 = 8

Question 8.
The top of a broken tree has its top touching the ground at a distance 15 m from the bottom, the angle made by the broken end with the ground is 30°. Then what is the length of the broken part? (3)
Answer:
Here, BAP is a tree and it gets broken at the point A and touches the ground at point C.

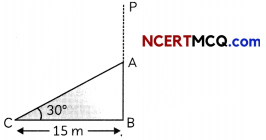
So, AC is the broken part.
In ∆ABC,
cos 30° = \(\frac{B C}{A C}\)
cos 30° = \(\frac{15}{A C}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{15}{A C}\)
⇒ AC = \(\frac{30}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= 10√3 m
= 10 × 1.732 m
= 17.32 m

Caution:
The three main functions in trigonometry are sine, cosine and tangent.
sine function : sin θ = \(\frac{\text { Oppositeside }}{\text { Hypotenuse }}\)
cosine function : cos θ = \(\frac{\text { Adjacent side }}{\text { Hypotenuse }}\)
tangent function : tan θ = \(\frac{\text { Opposite side }}{\text { Adjocent side }}\)

Question 9.
In the given figure, the diameters, of two wheels have measures 4 cm and 2 cm. Determine the lengths of the belts AD and BC that pass around the wheels if it is given that belts cross each other at right angles. (3)

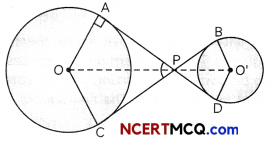
Answer:
Here, circle with centre O has radius 4 cm and circle with centre O’ has radius 2 cm.
In ∆OAP and ∆OCP
AP = PC [Tangent to a circle from same point]
OP = OP
OA = OC [radii of a circle]
∴ ∆OAP ≅ ∆OPB
∵ ∠APO = ∠CPO [By c.p.c.t]
But ∠APC = 90° [Given]
∴ ∠APO = 45°
In right ∆OAP = \(\frac{\mathrm{AP}}{\mathrm{OP}}\) = cot 45°
∴ AP = OP = 2 cm
Similarly, PD = 1 cm,
AD = AP + PD
= 1 + 2 = 3 cm
Now, AD = BC = 3 cm

Related Theory:
Congruency of two triangles and properties of trigonometric ratios are used to find the required side.

Question 10.
Prove that: The tangent at any point of a circle is perpendicular to the radius through the point of contact (O). At the point of contact the angle between radius and tangent to a circle is 90°. (3)
Answer:
Given: A circle (0, r) with centre 0. AB is a tangent to the circle at point P.
To Prove: OP ⊥ AB
Construction: Take any point Q an AB other than P and join OQ.

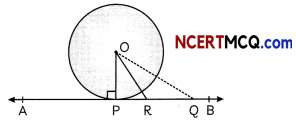
OQ > OR (i) (∵ greater than radii)
Similarly, OR>OP …(ii)
Thus, we find that among all such Line segments the line segment OP is the shortest, which is only possible when OP is perpendicular to AB
Hence, OP ⊥ AB

Caution:
Here, do the necessary construction to prove the desired result.

Section – C (16 marks)

Question 11.
The angle of depression of the top and bottom of building 50 m high as observed from the top of a tower are 30° and 60° respectively. Find the height of the tower and also the horizontal distances between the building and the tower. (4)
Answer:

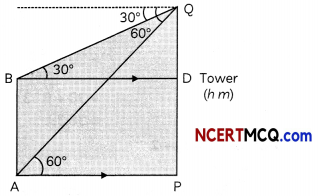
From right ∆BDQ,

⇒ \(\frac{50 \times 3}{2}\)
= 25 × 3
= 75 m
Thus, the height of the tower is 75 m.
From equation (i), we have,
AP = BD = \(\frac{\mathrm{PQ}}{\sqrt{3}}\) = \(\frac{75}{\sqrt{3}}\)
= 25√3
= 25 × 1.732
= 43:25 m

Question 12.
If h, C and v respectively represent the height, curved surface area and volume of a cone, prove that
C² = \(\frac{3 \pi v h^{3}+9 v^{2}}{h^{2}}\)
h2
OR
To maintain the beauty of a monument, the students of a school cleaned and painted the dome of the monument. The monument is in the form of a hemisphere. From inside, it was whitewashed by the students whose area is 249.48 m².
Find the volume of the air inside the dome. If white washing costs ₹ 2/m², how much does it costs ? (4)
Answer:

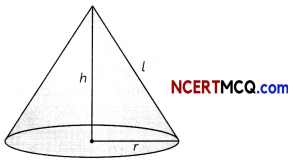
Here,
Volume of the cone, V = \(\frac{1}{3}\)πr² h
Curved surface area of cone (C)
= πrl
= πr\(\sqrt{h^{2}+r^{2}}\)
C² = π²r² (h² + r²) …(i)
So, 3πVh³ + 9V²
= 3π(\(\frac{1}{3}\)πr²h)h³ + 9(\(\frac{1}{9}\)π²r⁴h²)
= π²r²h⁴ + π²r⁴h²
= π²r²h² (h² + r²)
or \(\frac{3 \pi \mathrm{Vh}^{3}+9 \mathrm{~V}^{2}}{h^{2}}\) = π²r² (h² + r²) = C² [from (i)]

Related Theory:
Curved surface area of cone is calculated by using the slant height. And slant height (l) of the cone is
given by \(\sqrt{h^{2}+r^{2}}\)
OR
Here, dome of the monument is hemispherical in shape, which has to be whitewashed by the students.
Now, total area to be whitewashed = 249.48 m²
cost of white washing = ₹ 2/m²
∴ Total cost of white washing
= ₹ 2 × 249.48
= ₹ 498.96
Also, 2πr² = 249.48
r² = \(\frac{249.48}{2 \times 22}\) × 7
r = √158.76 = 12.6 m
Volume of air inside the dome = Volume of hemisphere
= \(\frac{2}{3}\) ≠ r³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 12.6 × 12.6 × 12.6
= 4191.264 m³

Question 13.
Case Study-1
A wax museum or waxworks usually consists of a collection of wax sculptures representing famous people from history and contemporary personalities exhibited in lifelike poses, wearing real clothes. A beautiful wax museum was built in taj city. Many people are visiting that museum on daily basis. A group of 71 people visited that museum on a particular day. The manager of the store want to make some calculation regarding the data of the number of peoples collected.

The table below shows the categorization on the basis of their ages.

Age (in years)	No. of persons
Less than 10	3
Less than 20	12
Less than 30	20
Less than 40	44
Less than 50	50
Less than 60	71

Now, answer the following questions:
(A) If true class limits are made, then what will be the last class interval. (2)
Answer:
Explanation: Here class interval formed

C.I.	f	cf
0-10	3	3
10-20	9	12
20-30	8	20
30-40	24	44
40-50	6	50
50-60	21	71

Then, last class interval is 50 – 60

(B) What is the median of the given data? (2)
Answer:

C.I.	f	cf
0-10	3	3
10-20	9	12
20-30	8	20
30-40	24	44
40-50	6	50
50-60	21	71
	71

Here, \(\frac{N}{2}\) = \(\frac{71}{2}\) = 35.2
Then, median class is 30 – 40
Median = l + \(\frac{\frac{N}{2}-c f}{f}\) × h
= 30 + \(\frac{35.2-20}{24}\) × 10
= 30 + \(\frac{15.2}{24}\)
= 30 + 6.33
= 36.33.

Question 14.
Case Study-2
A busy area is there in the shopping market of Gwalior. It was decided to make some parking lots to resolved the parking issues in the market.

As shown in the above figure, there are two squares. These of them are the spaces needed to be given to the parking area of cars near a mall in the market. The first square i.e. ABCD has side ‘a’ and another square PQRS has side ‘P’
The sum of the areas of two squares is 640 m2 and difference in their perimeter be 64 m.
Answer the following questions:
(A) What is length of the side of small parking area? (2)
Answer:
8 m
Explanation: A.T.Q. the side of square ABCD is a cm.
∴ Its area = a²
Similarly, for second square, PQRS, whose side is p cm, area = p²
∴ a² + p² = 640
or p² = 640 – a² …… (i)
And 4p – 4a = 64
⇒ p – a = 16 …(ii)
(Using (i) and (ii), we get
⇒ (16 + a)² = 164 – a²
⇒ 256 + a² + 32a = 640 – a²
⇒ 2a²+ 32a – 384 = 0
⇒ a² + 16a – 192 = 0
⇒ a² + 24a – 8a – 192 =0
⇒ a(a + 24) – 8(a + 24) = 0
⇒ a = 8, – 24
∴ a = 8 m

(B) What is the total area available for the parking lot in the form of big square? (2)
Answer:
Since, p – a =16
p = 16 + a
= 16 + 8 [from (i)]
= 24 m
Area of square PQRS = p × p
= 24 × 24 = 574 m²