CBSE Sample Papers for Class 10 Maths Basic Term 2 Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Basic Term 2 Set 3 with Solutions

Time allowed: 2 hours
Maximum Marks: 40

General Instructions:

• The question paper consists of 14 questions divided into 3 sections A, B, C.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one questions.
• Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one questions. It contains two case study based questions.

Section – A (12 marks)

Question 1.
Solve the give quadratic equation for the value of x:
\(\), ; x = ≠ -2, \(\frac{3}{2}\) (2)
Answer:
We have, = \(\frac{x+3}{x+2}=\frac{3 x-7}{2 x-3}\)
⇒ (x + 3)(2x – 3) = (3x – 7)(x + 2)
⇒ 2x² + 6x – 3x – 9 = 3x² – 7x + 6x – 14
⇒ 2x² + 3x – 9 = 3x² – x – 14
⇒ x² – 4x – 5 = 0
⇒ x² – 5x + x – 5 = 0
⇒ x(x – 5) + 1(x – 5) = 0
⇒ x = 5, -1

Question 2.
The circumference of the base of a 9 m high wooden solid cone is 44 m. Then, evaLuate the volume of the cone. [Use it π = \(\frac{22}{7}\)]
OR
The Length of a hall is 20 m and width is 16 m. The sum of the areas of the floor and the flat roof is equal to the sum of the four walls. Find the height and the volume of the hall (2)
Answer:
Let, the radius of the base be r m and height.
h = 9m
Circumference of base
2πr = 44
r = \(\frac{44}{2π}\)
=7m
Volume of cone = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 9
= \(\frac{1}{3}\) × 22 × 7 × 9
= 462 m²

Related Theory:
Circumference of cittuiar base is the boundary of that base i.e. its perimeter, which could be used the calculate the radius.
OR
Let, the height of the hail be h m
Length of the hail = 20 m
Breadth of the hail = 16 m
Then, sum of the oreas of the four wail.
= 2(l + b) × h m²
= 2(20 + 16) h
= 72 h m²

Sum of the areas of the floor and the flat roof
= (20 × 16 + 20 × 16) = 640m²
It is given that sum of the areas of the four walls is equal to the sum of the areas of the floor and the roof
72h = 640
⇒ h = \(\frac{640}{72}\)
= \(\frac{80}{9}\)
= 8.88 m
So, height of the wall = 8.88 m
Volume of the hati = 20 × 16 × 8.88
= 2844.4 m³

Question 3.
Data regarding heights of students of class X of model school, Dehradun is given below Calculate the average height of students of the class.

Height (in cm)	No. of Students
150-156	4
156-162	7
162-168	15
168-174	8
174-180	6

Answer:

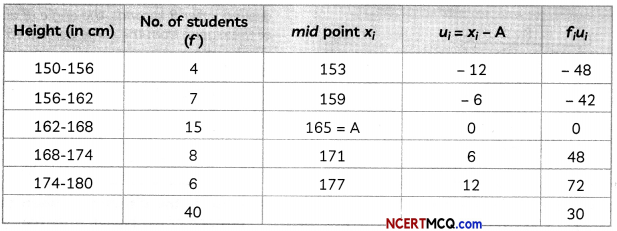
x̄ = A + \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= 165 + \(\left(\frac{30}{40}\right)\)
= 165 + 0.75
= 165.75

Question 4.
The sum of squares of three consecutive positive integers ore 50. Then what are the three integers? (2)
Answer:
Consider three consecutive integer as x, x + 1 and x + 2.
A.T.Q x² + (x + 1)² + (x + 2)² = 50
⇒ x² + x² + 1 + 2x + x² + 4 + 4x² = 50
⇒ 3x² + 6x – 45 = 0
⇒ 3(x² + 2x – 15) = 0
⇒ x² + 2x – 15 = 0
⇒ x² + 5x – 3x – 15 = 0
⇒ x(x + 5) – 3(x + 5) = 0
⇒ x = 3, -5
x ≠ -5 (rejected)
∴ Integers are 3, 4, 5

Question 5.
In the AP, 9, 17, 25…., how many terms should should be taken, to get a sum of 636? (2)
Answer:
Given A.P. is 9, 17, 25
Then a = 9,
d = 17 – 9 = 8
S_n = 636

Now, by formula
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
636= \(\frac{1}{2}\)[2 × 9 + (n – 1) × 8]
1272 = n[18 + 8n – 8]
1272 = (10 + 8n) × n
8n² + 10n – 1272 = 0
4n² + 5n – 636 = 0
4n² + 53n – 48n – 636 = 0
n(4n + 53) – 12(4n + 53) = 0
n = 12
or n = \(\frac{-53}{4}\) (rejected)
∴ n = 12

Question 6.
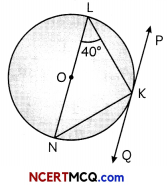
In the figure, O is the centre the circle and ∠N is a diameter. If PQ is a tangent to the circle at K and ∠KL.N = 40°, then find ∠PKL

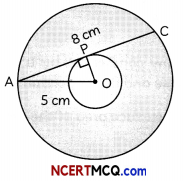
Two concentric circLe are there, the radius of outer circle ¡s 5 cm and the chord AC of Length 8 cm ¡s a tangent to the inner circLe. What is the radius of the inner circle?

Answer:
Here, LN is the diameter of the circle and O is the centre of the circle.

Join OK in the given figure.

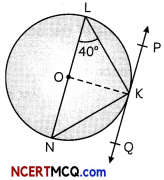
In ∆OLK,
QL = OK = radius of circle
∴ ∠OLK = ∠OKL = 40°

But. ∠OKP = 90°
∠PKL = ∠OKP – ∠OKL
= 90° – 40°
= 50°

Caution
Do the necessary construction for getting the desired angle.
OR
Here, OA = 5 cm, AC = 8 cm
OP ⊥ AC
∴ AP = PC
Then, AP = \(\frac{8}{2}\) = 4cm

In ∆OPA. by Pythagoras theorem
OA² = OP² + AP²
⇒ (5)² = Op² + (4)²
⇒ Op² = 25 – 16
= 9
⇒ OP =3cm
Hence, radius of smaller circle is 3 cm.

Section -B (12 marks)

Question 7.
An NGO working for the welfare of cancer patients, maintained its record as follows:

Age of patients (in years)	No. of patients
0-20	35
20-40	315
40-60	120
60-80	50

Find modal age of the patient. (3)
Answer:
Here, maximum frequency is 315 and the class corresponding to the frequency is 20-40.
Now, l = 20
f₁ = 315
f₀ = 35
f₂ = 120

Now, Mode = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) × h
= 20 + \(\frac{315-35}{2 \times 35-35-120}\) × h
= 20 + \(\frac{280}{475}\) × 20
= 20 + 11.79 = 31.79
Hence, modal age of patients is 31.79 ≈ 32 years.

Question 8.
Two men are on the opposite sides of a tower. They observe the angle of elevation of the top of the tower as 30° and 45° respectively. If the height of the tower is 50 m, find the distance between the two men. (3)
Answer:
Here, AB is a tower and C and D are the points of observation on either side of the tower.

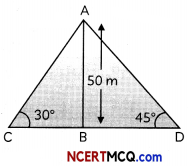
In ∆ABC
ton 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
\(\frac{1}{\sqrt{3}}=\frac{50}{B C}\)
BC = 50√3 m

In ∆ABD,
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
= \(\frac{50}{\mathrm{BD}}\)
BD = 50 m
Distance between 2 men, CD = BC + BD
= 50√3+50
= 50(√3+1)
= 50 × 2.732 = 136.6 m

Question 9.
In the figure shown, two circles touch each other externally at C. Prove that the common tangent at C bisects the other two common tangents.

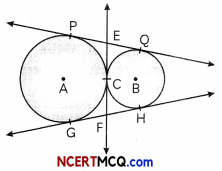
Answer:
Given: Let PQ and GH are the common tangents to both circles and common tangent at C meets PQ at E and GH at F.
To Prove: EF bisects PQ and GH.
Proof: Tangents’ drawn from an external point to a circle are equal.
EP = EC …(i)
and EQ = EC ,..(ii)
From (i) and (ii)
⇒ EP = EQ
⇒ PQ, is bisected by EF at E.
Similarly, GH is bisected by EF at F.
∴ The common tangent EF drawn at C bisects other two common tangents.
Hence, proved

Question 10.
50 students enter for a school javelin throw competition. The distance (in metres) thrown are recorded below:

Distance (in m)	No. of Students
0-20	6
20-40	11
40-60	17
60-80	12
80-100	4

Construct a cumulative frequency table and determine the median value of the distance covered.
OR
In the given data, values are arranged so that, the value of k is missing, if the mean of the following distribution is 20.

x	f
15	2
17	3
19	4
20 + k	5k
23	6

Answer:

Distance in (m)	No. of Students f	c.f
0-20	6	6
20-40	11	17
40-60	17	34
60-80	12	46
80-100	4	50
	Total = 50

Then \(\frac{\mathrm{N}}{2}=\frac{50}{2}\) = 25
The median class is 40-60
Now l = 40
c.f. = 17
f = 17
h = 20

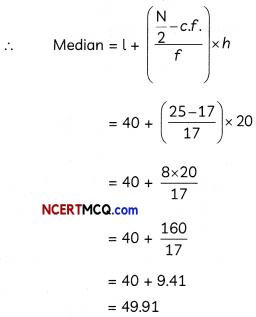
Caution:
Cumulative frequency in the formula of median is of the class prior to the median class.
OR
The given Date is:

xi	fi	fixi
15	2	30
17	3	51
19	4	76
20 + k	5k	100k + 5k2
23	6	138
Total	Σfi =5k+15	Σfixi = 295 + 100k + 5k2

Now, Mean = 20
∴ Mean = l
20 =
⇒ 295 + 100k + 5k² = (5k + 15)20
⇒ 295+ 100k + 5k² = 100k + 300
⇒ 295 + 100k+ 5k- 100k – 300 = 0
⇒ 5k² – 5 = 0
k² – 1 = 0
(k – 1)(k + 1) = 0
If k + 1 = 0, k = -1 (not possible)
If k – 1 = 0, k = 1
Hence, required value of k is 1.

Section – C (16 marks)

Question 11.
If a₁, a₂ … a_n-1, an are in AP then prove that: (4)

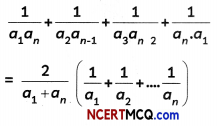
Answer:
Let first term and common difference of an AP be a₁ and d₁ respectively.

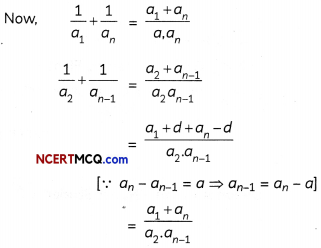
Similarly,
\(\frac{1}{a_{3}}+\frac{1}{a_{n-2}}=\frac{a_{1}+a_{n}}{a_{3} \cdot a_{n}}\)
\(\frac{1}{a_{n}}+\frac{1}{a_{1}}=\frac{a_{1}+a_{n}}{a_{1} \cdot a_{n}}\)
On adding all the above, we get

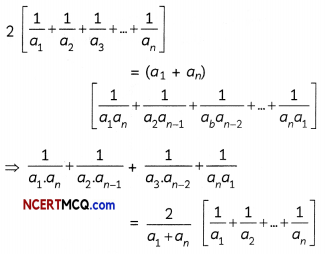
Hence Proved

Question 12.
Water is flowing at the rate of 2.52 km/hr, through a cylindrical pipe into a cylindrical tank, radius of whose base is 40 cm. If the increase in the level of water in tank, in half an hour is 3.15 m, find the internal diameter of the pipe.
OR
A hollow cone is cut by a plane parallel to the base and upper portion is removed. If the curved surface area of the remainder is \(\frac{8}{9}\) of the curved surface area of the whole cone, then find the ratio of the line segments into which the cone’s altitude is divided by the plane. (4)
Answer:
Let r be the internaL radius of the pipe
Radius of base of tank, R = 40cm
= \(\frac{40}{100}\)m
= \(\frac{2}{5}\) m
Level of water raised in tank (H) = 3.15 m
If the flow rate of water in an hour = 2.52 km
= 2520 m
Then, the flow rate in half and hour
\(\frac{2520}{2}\)
= 1260 m
So, height of water level (h) = 1260 m
Volume of tank = Volume of pipe
πr²h = πR²H

∴ Internal diameter of pipe = 2r = 2 x 2 = 4 cm
Hence, internal diameter of pipe = 154 cm.
OR
In the figure. the smaller cone APQ has been cut off through the plane PQ ∥ BC Let r and R be the radii of the smaller and bigger cones and l and L be their slant heights respectively.

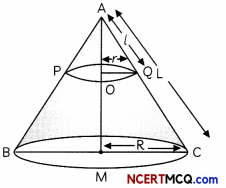
Here, QQ = r, MC = R,
AQ = l and AC = L
Now, ∆AOQ ~ ∆AMC
⇒ \(\frac{\mathrm{OQ}}{\mathrm{MC}}=\frac{\mathrm{AQ}}{\mathrm{AC}}\)
⇒ \(\frac{r}{R}=\frac{l}{L}\)
⇒ r = \(\frac{\mathrm{Rl}}{\mathrm{L}}\)

Since, curved surface area of the remainder = \(\frac{8}{9}\) of the curved surface area of the whole cone
CSA of smaller cone = \(\frac{1}{9}\) of the CSA of the whole cone

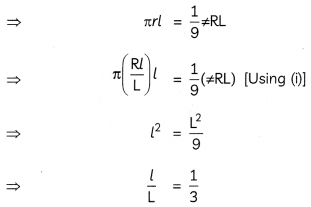
Now, again in simitar triangles, AQQ and AMC,
we have

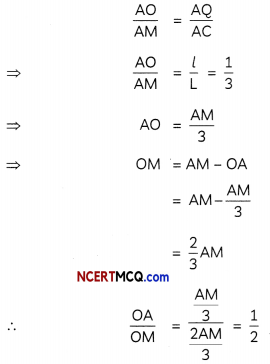
Hence, the required ratio of the heights = 1 : 2

Caution:
Use the property of similar triangles to calculate the unknown height and radius

Question 13.
Case Study-1
A fountain word is derived from a Latin word Tons’ meaning source or spring, is a decorative reservoir used for discharging water. These fountains can be used any where in parks, hoteLs etc. to beautify the ambience. Committee of Nehru garden want to make their garden more attractive and beautiful so they decided to place, a fountain is placed for the attraction in the middle of the park. This fountain is placed such that it is in the shape of the circle and four poles are placed at the corners of the park. A cloth is placed such that it joins the poles of the park surrounding the fountain:


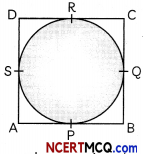
Now, answer the question that follows:
(A) In this of DR = 8 cm and AD 13 cm, them what is the length of AP? (2)
(B) If ∠PAS = 90° and O is the centre of the circle and AP = 5 cm, then what is the radius of the circle? (2)
Answer:
(A) As Length of the tangent drawn Worn an external point to a drde are equal
∴ DR = DS = 8cm
Then, AS = AD – DS
= 13 – 8
= 5 cm
But AP = AS = 5cm

(B) It O Is the Centre of the circle then
∠OSA = 90
∠OPA = 90°
∠PAS = 90°
Then, APOS is a square
AP = OP = OS = AS = 5 cm.

Question 14.
Case Study-2
On Sunday evening, while having evening tea, Rajesh was roaming in his courtyard. He was very much interested in bird watching and a great nature lover. Suddenly, he observes a pigeon sitting on the top of a pole of height 54 m from the ground. The height of Raju is 4m. The angle of elevation of the pigeon from the eyes of boy at any instant is 60°. The pigeon flies away horizontally in such a way that it remained at a constant height from the ground. After 8 seconds, the angle of elevation of the pigeon from the same point is 45°.

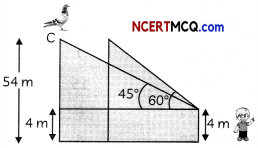
(A) What is the distance between the first position of the pigeon from the cycles of the boy? (2)
(B) What is the distance convered by pigeon in 8 second? (2)
Answer:
Case Study-2
(A) Distance of first position of pigeon from the eyes of boy = AC

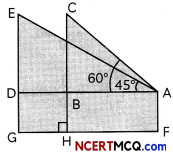
In ∆ABC
Sin 60° = \(\frac{B C}{A C}\)
AC = \(\frac{\mathrm{CH}-\mathrm{BH}}{\sin 60^{\circ}}\)
AC = \(\frac{54-4}{\sqrt{3} / 2}\)
= \(\frac{100}{\sqrt{3}}\) m

(B) In ∆AED, tan 45° = \(\)
⇒ AD = BC = 50 m (ED = BC)
Now, distance between two positions of pigeon = EC
But, EC = BD = AD – AB
= 50 – \(\frac{50}{\sqrt{3}}\)
= \(\frac{50(1.73-1)}{1.73}\)
= 21.09 m.