CBSE Sample Papers for Class 10 Maths Basic Term 2 Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths BasicTerm 2 Set 2 with Solutions

Time allowed: 2 hours
Maximum Marks: 40

General Instructions:

• The question paper consists of 14 questions divided into 3 sections A, B, C.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one questions.
• Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one questions. It contains two case study based questions.

Section – A (12 marks)

Question 1.
If the roots of the quadratic equation ax² + bx + c = 0 are sin α and cos α, then prove that a² + 2ac = b². (2)
Answer:
The roots of the equation ax² + bx + c = 0 are sin α and cos α.
∴ Sum of roots i.e.
⇒ sin α + cos α = \(\frac{-b}{a}\) ….. (i)
and products of roots
sin α + cos α = \(\frac{c}{a}\) ….. (ii)
From equation (i)
(sin α + cos α)² = \(\left(\frac{-b}{a}\right)^{2}\)
⇒ sin² α + cos² α + 2 sin α cos α
= \(\frac{b^{2}}{a^{2}}\)
⇒ 1 + 2 × \(\frac{c}{a}\) = \(\frac{b^{2}}{a^{2}}\) [from (ii)]
⇒ 1 + \(\frac{2c}{a}\) = \(\frac{b^{2}}{a^{2}}\)
⇒ a + 2c = \(\frac{b^{2}}{a}\)
⇒ a² + 2ac = b²

Question 2.
If in a cone, its height is tripled and radius is doubled, then by how much times does its volume increases ?
OR
If the total surface area of a solid hemisphere is 462 cm², then find its volume? [Take π = \(\frac{22}{7}\)] (2)
Answer:
Let, the height of cone be h and its radius be r units
Then, volume of cone = \(\frac{1}{3}\) ≠ r²h
If new height, H = 3h
New radius, R = 2r
Then,
New volume of cone = \(\frac{1}{3}\) ≠ R²h
= \(\frac{1}{3}\) ≠ (2r)² × 3h
= \(\frac{1}{3}\)(12 ≠ r²h)
= 12(\(\frac{1}{3}\)πr²h)
= 12 volume of initial cone
OR
Total surface area of hemisphere = 462 cm²
∴ 3πr²2 = 462
where r is the radius of the hemisphere
⇒ 3 × \(\frac{22}{7}\) × r² = 462
r² = \(\frac{462 \times 7}{3 \times 22}\) = 49
r = 7
(∵ Radius cannot be negative)
Volume of hemisphere = \(\frac{2}{3}\) ≠ r³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × 7 × 7 × 7
= \(\frac{2156}{3}\)
= 719 cm³ (approx)

Related Theory:
Hemisphere is the half of a sphere, which is obtained by cutting sphere into 2 halves

Question 3.
Write the relationship connecting three measures of central tendencies. Hence, find the median of the given data if mode is 24.5 and mean is 29.75. (2)
Answer:
According to the question,
Mode = 24.5
And Mean = 29.75
The relationship connecting the three measures of central tendency is:
3 Median = Mode + 2 × Mean
Now, mode = 24.5 and mean = 29.75
∴ 3 Median = 24.5 + 2 × 29.75
⇒ = 24.5 + 59.50
= 84.0 84
∴ Median = \(\frac{84}{3}\) = 28

Caution:
The correct empirical formula is important for calculating the value of the median.

Question 4.
In the AP 31, 28, 25 ….. is 0 is its any term ?
OR
What is the sum of the odd numbers between 0 and 50? (2)
Answer:
Here, A.P. is 31, 28, 25…
Then a = 31,
d = 28 – 31 = – 3
Let, n^th term be 0
∴ 0 = 31 + (n – 1)(- 3)
– 31 = – 3n + 3
⇒ – 3n = – 34
n = \(\frac{34}{3}\)
which is not possible,
Therefore, 0 is not a term of the given A.P.
OR
Odd numbers between 0 and 50 be 1, 3, 5, 7 …49
Here, a = 1,
d = 3 – 1 = 2
a_n = 49
We have, a_n = a + (n – 1)d
1 + (n – 1) × 2 = 49
⇒ 2 (n – 1) = 48
⇒ n – 1 = 24
⇒ n = 25
Then, S₂₅ = \(\frac{n}{2}\)(a + l)
= \(\frac{n}{2}\)[a + a₂₅]
= \(\frac{25}{2}\) (1 + 49)
= \(\frac{25}{2}\) × 50
= 25 × 25
= 625

Question 5.
From the following distribution, what is the median class (2)

Cost of living index	No. of weeks
1400-1550	8
1550-1700	15
1700-1850	21
1850-2000	8

Answer:

Cost of living index	No. of week(f)	c.f.
1400-1550	8	8
1550-1700	15	23
1700-1850	21	44
1850-2000	8	52

Here, N = 52,
\(\frac{N}{2}\) = \(\frac{52}{2}\)
= 26
Hence, median class is 1700-1850.

Question 6.
In the given figure AB and CD are two common tangents to two touching circles. If DC = 4 cm, then calculate the length of AB. (2)

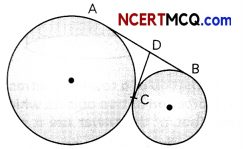
Answer:
Here, AD and DC are tangents from point D.
∴ AD = DC ……(i)
(Since tangents from an external point are equal)
And DB and DC are also tangents from point D
∴ DB = DC ……. (ii)
On adding (i) and (ii), we get,
AD + BD = DC + DC
AB = 2DC
⇒ AB = 2 × 4
= 8 cm

Section – B (12 Marks)

Question 7.
What is the middle term of the sequence formed by all three digit numbers which leave a remainder 5 when divided by 7. Also, find the sum of all numbers on both sides of the middle term separately. (3)
Answer:
According to the condition, the sequence formed will be 103, 110, …….. 999
Since 999 = 103 + (n – 1) × 7
⇒ (n – 1) × 7 = 999 – 103
⇒ (n – 1) × 7 = 896
⇒ n – 1 = 128
⇒ n = 129
Therefore,
\(\frac{129+1}{2}\) = 65^th term is the middle term
Middle term a₆₅ = 103 + 64 × 7 = 551
Sum of first 64 terms = 32[2 × 103 + 63 × 7] = 20704
Sum of last 64 terms = 32[2 × 558 + 63 × 7] = 49824

Caution:
First evaluate the number of the terms in the series, to get the middle term.

Question 8.
In Gokuldham society, a rectangular park is needed to be designed such that, its breadth is 3m less than its length. Its area is to be 4 sq. m more than the area of the park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of the altitude 12m. What is the length and breadth of the park.
OR
Vikram wants to make a show piece, in shape of a right angled ‘triangle’. For doing so, he took three rods together in the shape of a right – angled triangle. In this the hypotenuse is to be 2 cm longer than the base and 4 cm longer than the altitude. What should be the lengths of the rods? (3)
Answer:
Let, the Length of the park be ‘x’ m
Then, breadth of the park be (x – 3)m
Now, area of triangular park
= \(\frac{1}{2}\) × 12 × (x – 3)
= 6(x – 3)
And, area of rectangular park
= 6(x – 3) + 4
= 6x – 18 + 4
= 6x – 14
A.T.Q.
6x – 14 = x(x – 3)
⇒ 6x – 14 = x² – 3x
⇒ x² – 3x – 6x + 14 = 0
⇒ x² – 9x + 14 = 0
⇒ x² – 7x – 2x + 14 = 0
⇒ x(x – 7) – 2(x – 7) = 0
⇒ x = 7, 2
x = 2 is rejected
∴ x = 7 cm
Hence, length of park is 7 cm, and breadth is 4 cm.
OR
Let, the hypotenuse of the triangle be x cm.
A.T.Q.
Base of triangle = (x – 2) cm
Altitude of triangle = (x – 4) cm
By Pythagoras theorem,
x² = (x – 2)² + (x – 4)²
⇒ x² = x² + 4 – 4x + x² + 16 – 8x
⇒ x² – 12x + 20 = 0
⇒ x² – 10x – 2x + 20 = 0
⇒ x(x – 10) – 2(x – 10) = 0
⇒ (x – 2) (x – 10) = 0
⇒ x = 2, 10
Rejecting x = 2 we get, x = 10
Hypotenuse, x = 10 cm
Base = x – 2 = 10 – 2 = 8cm
Altitude = x – 4
= 10 – 4 = 6 cm.

Question 9.
In the adjoining figure, O is the centre of the circle. Then prove that ∠BAT = ∠ACB. (3)

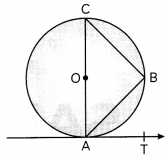
Answer:
Given: A circle with centre O. AC is its diameter.
AB and BC are two chords.
To prove: ∠BAT = ∠ACB

Proof:
∴ In ∆ABC,
∠ABC = 90° (Angle in a semicircle)
∴ ∠BAC = 90° – ∠ACB …… (i)
But ∠CAT = 90°
∴ ∠BAT = 90° – ∠CAB …… (ii)
From (i) and (ii)
∠BAT = 90° – (90° – ∠ACB)
∠BAT = ∠ACB
Hence proved.

Question 10.
From the top of a building 100 m high, the angle of depression of two objects are on the same side observed to be 45° and 60°. What is the distance between the objects. (3 )
Answer:
Here, AB is the building of height 100 m. Points P and Q are on the same side of the building, with angle of depression as 45° and 60°.

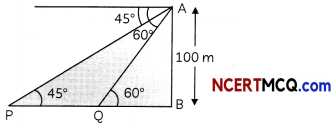
Now, in ∆ABP

Section – C (16 marks)

Question 11.
A building is in the from of a cylinder surmounted by a hemispherical dome. The base diameter of the dome is equal to \(\frac{2}{3}\) of the total height of the building. Find the height of the building, if it contains 67\(\frac{1}{27}\) m³ of air.
OR
A 55 cm high cylindrical lamp – shade has small decorative mirror on its either ends upto a width of 10 cm and 50 mm thick wire wound around all over to cover the middle part. How many revolutions will the wire take to cover it ?

Answer:
Let, the radius of the hemispherical dome be r meters and the total height of the building be h meters.

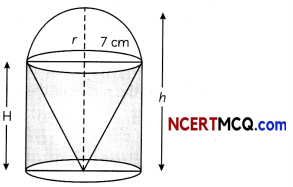
Since, the base diameter of the dome is equal to \(\frac{2}{3}\) of the total height, therefore
2r = \(\frac{2h}{3}\)
⇒ r = \(\frac{h}{3}\)m
Let, H metres be the height of the cylindrical portion.
Therefore, H = h – \(\frac{h}{3}\) = \(\frac{2h}{3}\)
Volume of the air inside the building = Volume of air inside the dome + Volume of air inside the cylinder

Related Theory:
Cub/c units are the unit of volume. Square units are the unit area. So if air is given, it occupies space or volume of the dome.
OR
Here, height of cylinder in which wire is wound
= 55 – 10 – 10 = 35 cm
So, the portion need to be covered by wire =
2πR(35)
2πR (35) = 2πR × \(\frac{50}{10}\) cm × No. of revolutions
where, R is the radius of the cylinder
⇒ 35 = \(\frac{50}{10}\) × No. of revolution
⇒ No. of revolutions = 7

Question 12.
From the top of a tower h metres high, angle of depression of two objects which are in line with foot of the tower are α and β (β > α). Find the distance between the objects. (4)
Answer:
Let AB represent the tower of height h metres.
P and Q be the position of the two objects on the ground. We need to determine the distance PQ.

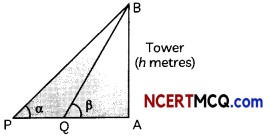
From ∆QAB, we have
tan β = \(\frac{h}{\mathrm{QA}}\)
⇒ QA = h cot β …(i)
From ∆PAB, we have
tan α = \(\frac{A B}{P A}\)
= \(\frac{h}{P A}\)
⇒ PA = h cot a …(ii)
Further, PQ = PA – QA
= h cot α – h cot β (from (ii) and (iii))
= h (cot α – cot β)

Caution:
Since, β > α, then point of observation of angle p is closer to the tower than angle observation point of α.

Question 13.
Case Study-1
In new housing society, a park in the shape of a circle is made for children. The society member want to make a green zone around the park, by planting the trees around it in the form of tangent to the circle. Therd is a circular park of radius 24 m and there is a pole at a distance of 26 m from the centre of the park as shown in the figure. It is planned to enclose the park by planting trees along line segments PQ and PR tangential to the park.

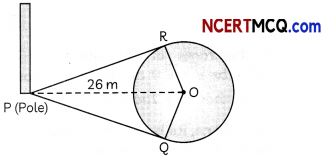
Answer:
(A) What is the length of PQ and PR (2)
Answer:

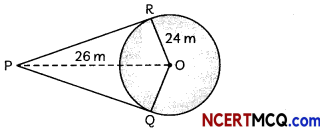
right angled triangle PRO,
We have,
PR = \(\sqrt{\mathrm{PO}^{2}-\mathrm{RO}^{2}}\)
= \(\sqrt{26^{2}-24^{2}}\)
= \(\sqrt{676-576}\)
= √100
= 10 m
⇒ PR = PQ = 10 m

(B) If six trees are planted along each tangential line segments at equal distances, find the distance between any two consecutive trees. (2)
Answer:
As six trees are to be planted along PQ and PR each,

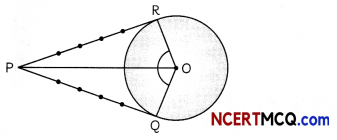
Let’s assume the distance between two consecutive trees is x.
Total trees are at 5 equal distances
Hence, 5x = 10
x = 2

Related Theory:
Here, the property of tangents that length drawn from a point outside the circle is equal in length.

Question 14.
Case Study-2
Bakery items like breads, buns, biscuits, cakes etc. have a definite life (in hours). They get stale very quickly, many microorganism persist on it, it not consumed timely. A bakery product manufacturer wants to know the lifetime of buns, pizza base and kulchas. For doing so, he tested the life time of 400 packets of pizza base.

Life time (in hours)	No. of packets (c.f.)
150-200	14
200-250	60
250-300	130
300-350	211
350-400	300
400-450	360
450-500	400

(A) What is the frequency of the class interval 300 – 350? (2)
Answer:

Life time (in hours)	No. of packets (c.f.)	f
150-200	14	14
200-250	60	46
250-300	130	70
300-350	211	81
350-400	300	89
400-450	360	60
450-500	400	40

The frequency of class interval 300 – 350 is 81.

(B) What is average life time of a pizza base (2)
Answer:

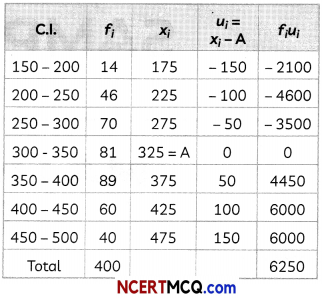
Then, x̄ = A + \(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\)
= 325 + \(\frac{6250}{400}\)
= 325 + 15.625
= 340.625
= 341 hours