CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 3

CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 3 are part of CBSE Sample Papers for Class 10 Maths in Hindi Medium. Here we have given CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 3.

CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 3

Board	CBSE
Class	10
Subject	Maths
Sample Paper Set	Paper 3
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 3 of Solved CBSE Sample Papers for Class 10 Maths in Hindi Medium is given below with free PDF download Answers.

Time allowed: 3 hours
Maximum marks: 80

सामान्य निर्देश:

• सभी प्रश्न अनिवार्य हैं।
• इस प्रश्न-पत्र में 30 प्रश्न हैं।
• खण्ड A में प्रश्न संख्या 1-6 प्रश्न अतिलघुत्तरीय हैं जिनमें से प्रत्येक 1 अंक का है।
• खण्ड B में प्रश्न संख्या 7-12 प्रश्न लघुत्तरीय हैं जिनमें से प्रत्येक 2 अंक का है।
• खण्ड C में प्रश्न संख्या 13-22 प्रश्न दीर्घ उत्तरीय-I हैं जिनमें से प्रत्येक 3 अंक का है।
• खण्ड D में प्रश्न संख्या 23-30 प्रश्न दीर्घ उत्तरी-II हैं जिनमें से प्रत्येक 4 अंक का है।

SECTION A

प्रश्न संख्या 1 से 6 तक प्रत्येक प्रश्न का 1 अंक है।

Question 1.
यदि ΔABC ~ ΔRPQ है, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm और PQ = 10 तो QR की लंबाई ज्ञात कीजिए।

Question 2.
ΔABC एक समकोण त्रिभुज है जिसमें tan B = \(\frac { 12 }{ 5 }\), तो sin B का मान ज्ञात कीजिए।

Question 3.
एक समकोण त्रिभुज ABC में, ∠B समकोण है, BC = 12 सेमी तथा AB = 5 सेमी है। इस त्रिभुज के अंतर्गत खींचे गए वृत्त की त्रिज्या (सेमी में) ज्ञात कीजिए।

Question 4.
3 बच्चों के परिवार में, कम-से-कम एक लड़का होने की प्रायिकता ज्ञात कीजिए।

Question 5.
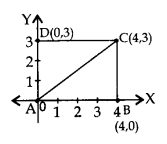
ABCD एक आयत है जिसके तीन शीर्ष B(4, 0), C(4, 3) तथा D(0, 3) हैं। आयत के एक विकर्ण की लंबाई ज्ञात कीजिए।

Question 6.
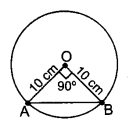
10 सेमी त्रिज्या के वृत्त की एक जीवा केंद्र पर समकोण अंतरित करती है। इस जीवा की लंबाई (सेमी में) ज्ञात कीजिए।

SECTION B

प्रश्न संख्या 7 से 12 तक प्रत्येक प्रश्न के 2 अंक हैं।

Question 7.
सिद्ध कीजिए कि 2 + 3√5 एक अपरिमेय संख्या है।

Question 8.
द्विघात समीकरण 3x² – 75 के शून्यक ज्ञात कीजिए तथा शून्यकों व गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए।

Question 9.
आकृति में, EF || AC, BC = 10 cm, AB = 13 cm तथा EC = 2 cm है। AF की लम्बाई ज्ञात कीजिए।

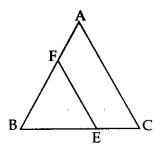
Question 10.
101 तथा 999 के बीच 2 और 5 दोनों से विभाज्य प्राकृत संख्याओं की संख्या ज्ञात कीजिए।

Question 11.
आकृति में, केंद्र O₁ तथा O₂ वाले दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ AB तथा CD बिंदु E पर काटती हैं। सिद्ध कीजिए कि AB = CD.

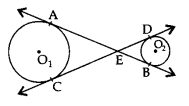
अथवा
एक समद्विबाहु त्रिभुज ABC, जिसमें AB = AC है, के अंतर्गत खींचा गया वृत्त, भुजाओं BC, CA तथा AB को क्रमशः बिंदुओं D, E तथा F पर स्पर्श करता है। सिद्ध कीजिए कि BD = DC है।

Question 12.
यदि एक ठोस अर्द्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल 462 वर्ग सेमी है, तो इसका आयतन ज्ञात कीजिए। [π = \(\frac { 22 }{ 7 }\) लीजिए]

SECTION C

प्रश्न संख्या 13 से 22 तक प्रत्येक प्रश्न के 3 अंक हैं।

Question 13.
एक द्विघात समीकरण ज्ञात करो। जिनके शून्यकों का योग व गुणनफल क्रमशः -8 तथा 12 है। अतः शून्यक ज्ञात करो।

Question 14.
दो संख्याएँ ज्ञात कीजिए जिनका योग 75 तथा 15 अंतर है।

Question 15.
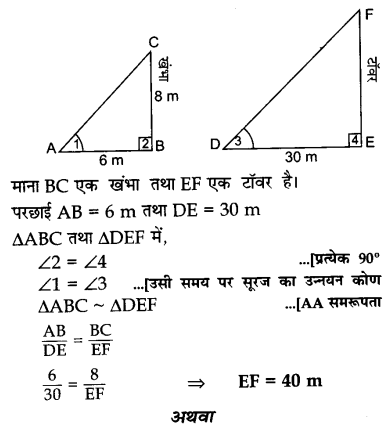
8m लंबे खंभे की भूमि पर छाया 6m लंबी है तथा उसी समय टॉवर की छाया की लंबाई 30 m है। टॉवर की ऊँचाई ज्ञात करो।
अथवा
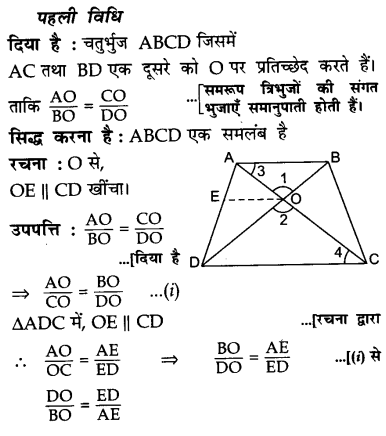
चतुर्भुज ABCD के विकर्ण एक दूसरे को बिंदु O पर प्रतिच्छेद करते हैं जिससे \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\)। दर्शाइये कि ABCD एक समलंब है।

Question 16.
यदि cos x = cos 40° . sin 50° + sin 40° . cos 50° है, तब x का मान ज्ञात कीजिए।

Question 17.
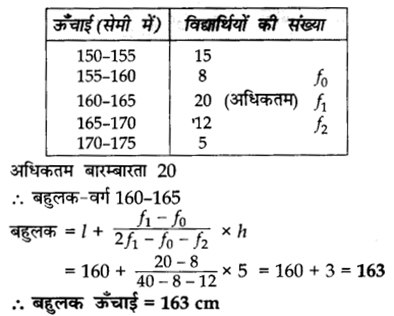
निम्नलिखित बारम्बारता सारणी कक्षा X के विद्यार्थियों की ऊँचाई को दर्शाती है:

बहुलक की ऊँचाई ज्ञात कीजिए।

Question 18.
52 पत्तों की ताश की एक गड्डी में से लाल रंग की बेगमें तथा काले रंग के गुलाम निकाल दिए गए। शेष पत्तों को अच्छी प्रकार फेंटने के बाद उनमें से यादृच्छया एक पत्ता निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाला गया पत्ता:
(i) एक बादशाह है।
(ii) लाल रंग का हो
(iii) एक तस्वीर वाला पत्ता हो
(iv) एक बेगम हो।

Question 19.
एक समांतर श्रेढी के 5वें और 9वें पदों का योगफल 30 है। यदि इसका 25वां पद इसके 8वें पद का तीन गुना है, तो समांतर श्रेढी ज्ञात कीजिए।

Question 20.
एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ 5 सेमी, 5.5 सेमी तथा 6.5 सेमी हैं। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ, दिए हुए त्रिभुज की संगत भुजाओं की \(\frac { 3 }{ 5 }\) गुनी हों।

Question 21.
यदि बिंदु P(k – 1, 2) बिंदुओं A(3, k) तथा B(k, 5) से समदूरस्थ हैं, तो k के मान ज्ञात कीजिए।
अथवा
वह अनुपात ज्ञात कीजिए जिसमें बिंदुओं A(3, -3) तथा B(-2, 7) को मिलाने वाला रेखाखण्ड x-अक्ष से विभाजित होता है। इस विभाजन बिंदु के निर्देशांक भी ज्ञात कीजिए।

Question 22.
6 मी चौड़ी तथा 1.5 मी गहरी एक नहर में पानी 4 किमी प्रति घण्टे की चाल से बह रहा है। 10 मिनट में यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी यदि सिंचाई के लिए 8 सेमी गहरे पानी की आवश्यकता है?
अथवा
आकृति में, ABCD एक समलंब है जिसका क्षेत्रफल 24.5 वर्ग सेमी है। इसमें AD || BC, ∠DAB = 90°, AD = 10 सेमी तथा BC = 4 सेमी है। यदि ABE एक वृत का चतुर्थांश है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। [π = \(\frac { 22 }{ 7 }\) लीजिए]

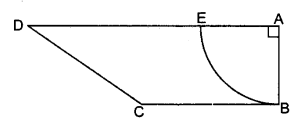
SECTION D

प्रश्न संख्या 23 से 30 तक प्रत्येक प्रश्न के 4 अंक हैं।

Question 23.
टैक्सी कम्पनी के मालिक ने सभी टैक्सियों के लिए पेट्रोल या डीज़ल के स्थान पर CNG इस्तेमाल करने का निर्णय किया। नगर में टैक्सी के भाड़े में एक नियत भाड़े के अतिरिक्त चली गई दूरी पर भाड़ा सम्मिलित किया जाता है। 12 km की दूरी के लिये भाड़ा ₹ 89 तथा 20 km के लिए भाड़ा ₹ 145 है।
(i) एक व्यक्ति को 30 km यात्रा करने पर कितना भाड़ा देना होगा?
(ii) मालिक ने पेट्रोल की जगह CNG को प्रयोग करने का निर्णय क्यों लिया?
अथवा
यदि बहुपद 3x⁴ – 4x³ – 16x² + 15x + 14 को अन्य बहुपद x² – 4, से भाग करने पर शेषफल px + q ज्ञात होता है। p तथा q का माने ज्ञात कीजिए।

Question 24.
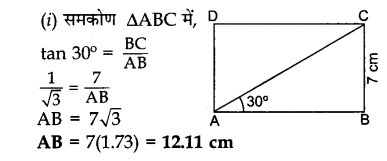
दी गई आकृति में, ABCD एक आयत है जिसकी चौड़ाई BC = 7 cm तथा ∠CAB = 30° है। आयत की भुजा की लम्बाई AB तथा विकर्ण AC की लम्बाई ज्ञात करो। यदि ∠CAB = 60° है तो भुजा AB का क्या माप होना चाहिए। [√3 = 1.73 तथा √2 = 1.41 लीजिए।]

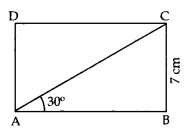
Question 25.
सिद्ध कीजिए b²x² – a²y² = a²b², यदि:
(i) x = a sec θ, y = b tan θ
(ii) x = a cosec θ, y = b cot θ

Question 26.
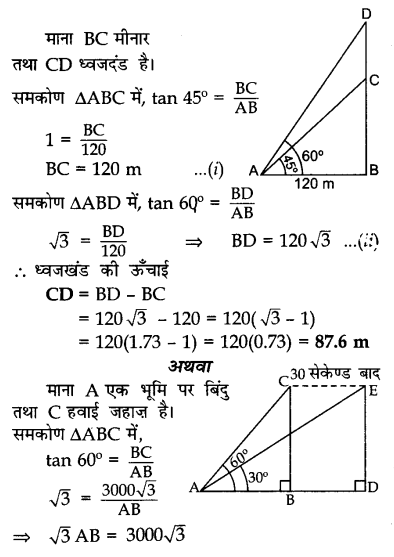
भूमि पर स्थित बिंदु A से 120 मी की दूरी पर स्थित एक मीनार के शिखर का उन्नयन कोण 45° है। यदि मीनार के शिखर पर लगे एक ध्वजदंड के ऊपरी सिरे का बिंदु A पर उन्नयन कोण 60° है, तो ध्वजदंड की ऊँचाई ज्ञात कीजिए। [√3 = 1.73 लीजिए]
अथवा
भूमि के एक बिंदु से एक वायुयान का उन्नयन कोण 60° है। 30 सेकंड की उड़ान के बाद यह उन्नयन कोण 30° हो जाता है। यदि यह वायुयान 3000√3 मी की अचर ऊँचाई पर उड़ रहा है, तो वायुयान की गति ज्ञात कीजिए।

Question 27.
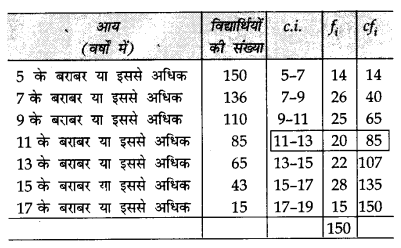
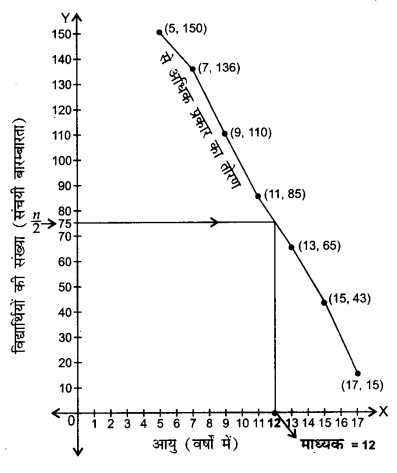
स्कूल में हुए ‘खेल-दिवस’ पर 150 विद्यार्थियों ने भाग लिया। निम्नलिखित सारणी उन विद्यार्थियों की आयु को दर्शाता है।

दिए गए आंकड़ों से ‘से अधिक’ प्रकार का तोरण बनाइए तथा वक्र से माध्यक ज्ञात कीजिए। उचित गणना द्वारा सत्यापन कीजिए।

Question 28.
एक नाव की शांत जल में चाल 18 km/h है। यदि नाव को 24 km धारा के प्रतिकूल जाने की तुलना में अनुकूल जाने पर 1 घंटा अधिक लगता है। धारा की चाल ज्ञात कीजिए।

Question 29.
आकृति में, 10 सेमी त्रिज्या के एक वृत्त की 16 सेमी लंबी एक जीवा PQ है। बिंदु P तथा बिंदु Q पर स्पर्श रेखाएँ परस्पर एक बिंदु T पर प्रतिच्छेद करती है। TP की लंबाई ज्ञात कीजिए।

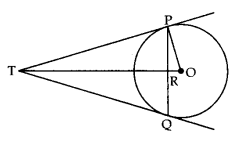
Question 30.
ऊपर से खुला एक बरतन शंकु के छिन्नक के आकार का है, जिसकी ऊँचाई 24 सेमी है तथा निचले तथा ऊपरी वृत्तीय सिरों की त्रिज्याएँ क्रमशः 8 सेमी तथा 20 सेमी है। ₹ 21 प्रति लीटर की दर से इस बरतन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। [π = \(\frac { 22 }{ 7 }\) लीजिए]
अथवा
एक तम्बू एक शंकु के छिन्नक के आकार का है जिस पर एक शंकु अध्यारोपित है, यदि छिन्नक के ऊपरी और निचले वृत्ताकार सिरों का व्यास क्रमशः 14 मी तथा 26 मी है, छिन्नक की ऊँचाई 8 मी है तथा अध्यारोपित शंक्वाकार भाग की तियर्क ऊँचाई 12 मी हो तो, तम्बू बनाने के लिए आवश्यक कैनवास का क्षेत्रफल ज्ञात कीजिए (माना गया है कि छिन्नक के ऊपरी वृत्ताकार की त्रिज्या तथा अध्यारोपित शंकु के आधार की त्रिज्या समान है)।

SOLUTIONS

Solution 1.

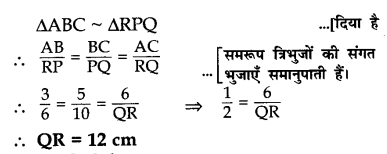
Solution 2.

Solution 3.

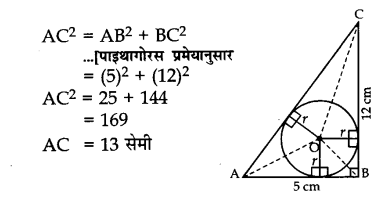
Solution 4.
कुल परिणाम, S = {bbb, bbg, ggb, geg}
कम से कम 1 लड़का = {bbb, bbg, ggb} = 3
P(कम से कम 1 लड़का) = \(\frac { 3 }{ 4 }\)

Solution 5.
AB = 4 इकाइयाँ
BC = 3 इकाइयाँ
AC² = AB² + BC² …[पाइथागोरस प्रमेयानुसार]
= (4)² + (3)² = 16 + 9 = 25
AC = 5 सेमी।

Solution 6.
AB² = OA² + OB² …[पाइथागोरस प्रमेयानुसार]
AB² = 10² + 10²
AB² = 2(10)²
AB = 10√2

Solution 7.
यदि हम इसके विपरीत मान लें 2 + 3√5 कि एक परिमेय संख्या है।
अतः हम ऐसी सहअभाज्य संख्याएँ a तथा b (b ≠ 0) ज्ञात कर सकते हैं कि 2 + 3√5 = \(\frac { a }{ b }\) समीकरण को पुनर्व्यवस्थित करने पर।
चूँकि a तथा b पूर्णांक हैं।
\(\frac { a }{ 3b }\) – \(\frac { 2 }{ 3 }\) एक परिमेय संख्या है अतः √5 एक परिमेय संख्या है जिससे इस तथ्य का विरोधाभास प्राप्त । होता है कि √5 एक अपरिमेय संख्या है।
इसलिए हम निष्कर्ष प्राप्त करते है कि 2 + 3√5 एक अपरिमेय संख्या है।

Solution 8.

Solution 9.

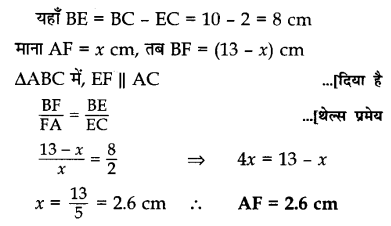
Solution 10.
2 और 5 दोनों से विभाज्य संख्याएँ : 110, 120, 130, …, 990
यहाँ a = 110, a = 120 – 110 = 10
a_n = 990
जैसा कि हम जानत हैं, : a + (n – 1) d = a_n
110 + (n – 1)(10) = 990
(n – 1) (10) = 990 – 110 = 880
(n – 1) = 88
n = 88 + 1 = 89

Solution 11.
EA = EC …(i) ….. [वृत्त के बाह्य बिंदु से खींची गई स्पर्श रेखाओं की लंबाई समान होती हैं।]
EB = ED …(ii)
EA + EB = EC + ED …[समीकरण (i) तथा (ii) को जोड़ने पर]
AB = CD
अथवा

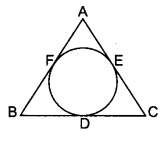
दिया है : एक ΔABC जिसमें एक अंत:वृत्त बिंदुओं D, E, तथा F पर त्रिभुज की भुजाओं BC, CA तथा AB को क्रमशः स्पर्श करता है। AB = AC
सिद्ध करना है : BD = CD
उपपत्ति : वृत्त की बाह्य बिंदु से खींची गई स्पर्श रेखाओं की लंबाई समान होती हैं।
AF = AE …..(i)
BF = BD …(ii)
CD = CE ….(iii)
(i), (ii) तथा (iii) को जोड़ने पर,
AF + BF + CD = AE + BD + CE
⇒ AB + CD = AC + BD
परंतु AB = AC …[दिया है।]
CD = BD

Solution 12.

Solution 13.
माना शून्यकों का योग (α + β) = S = -8
शून्यकों का गुणनफल (α x β) = P = 12
द्विद्यात समीकरण : x² – Sx + P = 0
⇒ x² – (-8)x + 12 = 0
⇒ x² + 8x + 12 = 0
⇒ x² + 6x + 2x + 12 = 0
⇒ x (x + 6) + 2 (x + 6) = 0
⇒ (x + 2)(x + 6) = 0
शून्यक हैं x + 2 = 0 अथवा x + 6 = 0
x = -2 अथवा x = -6

Solution 14.
माना x तथा y दो संख्याएँ हैं।
प्रश्नानुसार,
x + y = 75 …..(i)
x – y = ±15 …..(ii)

Solution 15.

Solution 16.
cos x = cos 40° sin 50° + sin 40° cos 50°
⇒ cos x = cos 40° sin(90° – 40°) + sin 40° . cos(90° – 40°)
⇒ cos x = cos 40° cos 40° + sin 40° sin 40° …… [ sin (90° – A) = cos A, cos (90° – A) = sin A ]
⇒ cos x = cos²40° + sin²40°
⇒ cos x = 1 …[cos²A + sin²A = 1]
⇒ cos x = cos 0°
⇒ x = 0°

Solution 17.

Solution 18.
लाल बेगमों की संख्या = 2
काले गुलामों की संख्या = 2
शेष पत्ते = 52 – 2 – 2 = 48
(i) P(एक बादशाह) = \(\frac { 4 }{ 48 }\) = \(\frac { 1 }{ 12 }\)
(ii) P(लाल रंग) = \(\frac { 24 }{ 48 }\) = \(\frac { 1 }{ 2 }\)
(iii) P(एक तस्वीर वाला पत्ता) = \(\frac { 8 }{ 48 }\) = \(\frac { 1 }{ 6 }\)
(iv) P(एक बेगम) = \(\frac { 2 }{ 48 }\) = \(\frac { 1 }{ 24 }\)

Solution 19.
दिया है : a₅ + a₉ = 30
a + 4d + a + 8d = 30 …[a_n = a + (n – 1)d]
2a + 12d = 30
a + 6d = 15 …[2 से भाग करने पर]
a = 15 – 6d …(i)
a₂₅ = 3(a₈)
a + 24d = 3(a + 7d)
15 – 6d + 24d = 3(15 – 6d + 7d) ….[(i) से]
15 + 18d = 3(15 + d)
15 + 18d = 45 + 3d
18d – 3d = 45 – 15
15d = 30
d = 2
(i) से, a = 15 – 6(2) = 15 – 12 = 3
A.P. है a, a + a, a + 2d, a + 3d, …
3, 5, 7, 9, ……..

Solution 20.

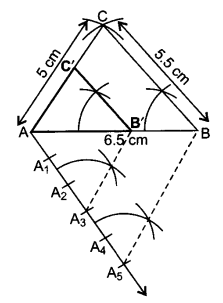
अत: ∆AB’C’ एक अभीष्ठ त्रिभुज है।

Solution 21.

Solution 22.

Solution 23.

Solution 24.

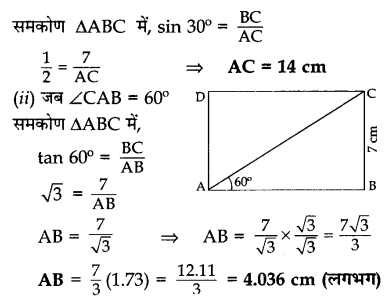
Solution 25.

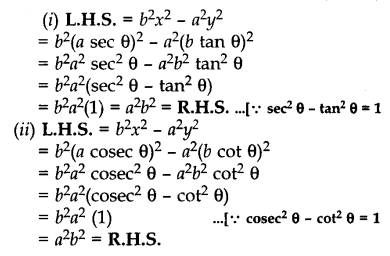
Solution 26.

Solution 27.

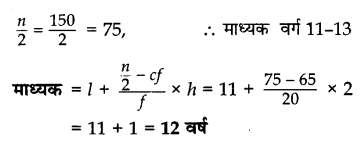
Solution 28.

Solution 29.

Solution 30.

We hope the CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 3 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 3, drop a comment below and we will get back to you at the earliest.