CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 4

CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 4 are part of CBSE Sample Papers for Class 10 Maths in Hindi Medium. Here we have given CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 4.

CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 4

Board

CBSE

Class

10

Subject

Maths

Sample Paper Set

Paper 4

Category

CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 4 of Solved CBSE Sample Papers for Class 10 Maths in Hindi Medium is given below with free PDF download Answers.

Time allowed: 3 hours
Maximum marks: 80

सामान्य निर्देश:

• सभी प्रश्न अनिवार्य हैं।
• इस प्रश्न-पत्र में 30 प्रश्न हैं।
• खण्ड A में प्रश्न संख्या 1-6 प्रश्न अतिलघुत्तरीय हैं जिनमें से प्रत्येक 1 अंक का है।
• खण्ड B में प्रश्न संख्या 7-12 प्रश्न लघुत्तरीय हैं जिनमें से प्रत्येक 2 अंक का है।
• खण्ड C में प्रश्न संख्या 13-22 प्रश्न दीर्घ उत्तरीय-I हैं जिनमें से प्रत्येक 3 अंक का है।
• खण्ड D में प्रश्न संख्या 23-30 प्रश्न दीर्घ उत्तरी-II हैं जिनमें से प्रत्येक 4 अंक का है।

SECTION A

प्रश्न संख्या 1 से 6 तक प्रत्येक प्रश्न 1 अंक का है।

Question 1.
दी गई आकृति में, यदि DE || BC, AE = 8 cm, EC = 2 cm तथा BC = 6 cm है, तो DE का मान ज्ञात कीजिए।

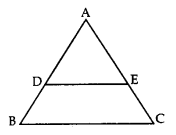
Question 2.
\(10\cdot \frac { 1-{ cot }^{ 2 }{ 45 }^{ 0 } }{ 1+{ sin }^{ 2 }{ 90 }^{ 0 } }\) का मान ज्ञात कीजिए।

Question 3.
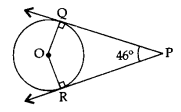
आकृति में, PQ तथा PR केंद्र O वाले वृत्त की दो स्पर्श रेखाएँ हैं। यदि ∠QPR = 46° है, तो ∠QOR का मान ज्ञात कीजिए।

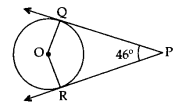
Question 4.
यदि दो भिन्न-भिन्न पासों को एक साथ उछाला जाए, तो दोनों पासों पर सम संख्या के आने की प्रायिकता ज्ञात कीजिए।

Question 5.
यदि बिंदु A(x, 2), B(-3, -4) तथा C(7, -5) संरेखी हैं, तो x को मान ज्ञात कीजिए।

Question 6.
ऊँचाई 45 सेमी तथा व्यास 4 सेमी वाले धातु के एक ठोस बेलन को पिघला कर 6 सेमी व्यास वाले ठोस गोले बनाए गए। ठोस गोलों की संख्या ज्ञात कीजिए।

SECTION B

प्रश्न संख्या 7 से 12 तक प्रत्येक प्रश्न के 2 अंक हैं।

Question 7.
भाजक के उस प्रधान घटक को ढूंढिए जिसे सरल रूप से व्यक्त की गई तर्कसंगत संख्या \(6.\bar { 12 }\) में व्यक्त किया है।

Question 8.
द्विघात समीकरण ज्ञात कीजिए जिसके शून्यकों का योग तथा गुणनफल क्रमशः √3 तथा \(\frac { 1 }{ \surd 3 }\) हो।

Question 9.
एक आयत ABCD में, E, AD को मध्यबिंदु है। यदि AD = 40 m तथा AB = 48 m है तो EB का मान ज्ञात कीजिए।
अथवा
निम्नलिखित सारणी एक कक्षा के विद्यार्थियों को मिले साप्ताहिक जेबखर्च को दर्शाती है। अधिकतम विद्यार्थियों को मिले जेबखर्च की गणना कीजिए।

Question 10.
द्विघात समीकरण 2x² + ax – a² = 0 को x के लिए हल कीजिए।

Question 11.
एक समांतर श्रेढी का प्रथम पद 5 तथा अंतिम पद 45 है। यदि इस श्रेढी के सभी पदों का योग 400 है, तो इसका सार्वअंतर ज्ञात कीजिए।

Question 12.
सिद्ध कीजिए कि वृत्त की दो समांतर स्पर्श रेखाओं के स्पर्श बिंदुओं को मिलाने वाला रेखाखण्ड वृत्त के केन्द्र से होकर जाता है।

SECTION C

प्रश्न संख्या 13 से 22 तक प्रत्येक प्रश्न के 3 अंक हैं।

Question 13.
सिद्ध कीजिए कि 3 + 2√3 एक अपरिमेय संख्या है।

Question 14.
एक आदमी की मासिक आय उसकी पत्नी की मासिक आय से ₹ 600 अधिक है। आदमी की आय के दसवें भाग तथा पत्नी की आय के छठे भाग का योग ₹ 1,500 है, जो कि उनकी मासिक बचत है। उनकी मासिक आय ज्ञात कीजिए।

Question 15.
जाँच कीजिए कि x – 1, बहुपद x³ – 8x² + 19x – 12 का एक गुणनखंड है या नहीं। विभाजन एल्गोरिथ्म को सत्यापित कीजिए।

Question 16.
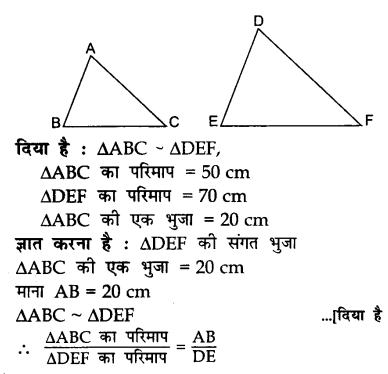
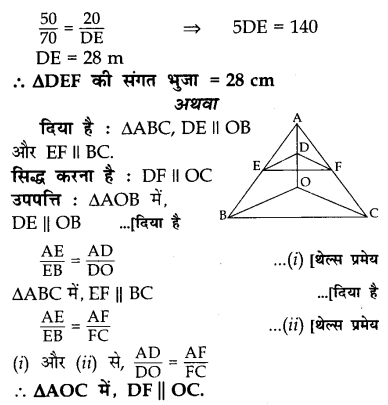
यदि दो समान त्रिभुज ABC और DEF की परिधि क्रमशः 50 cm और 70 cm और ∆ABC = 20 cm के एक तरफ है तो ∆DEF के संबंधित पक्ष को ढूंढिए।
अथवा
आकृति में, यदि DE || OB तथा EF || BC है, सिद्ध कीजिए कि DF || OC.

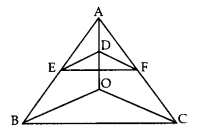
Question 17.
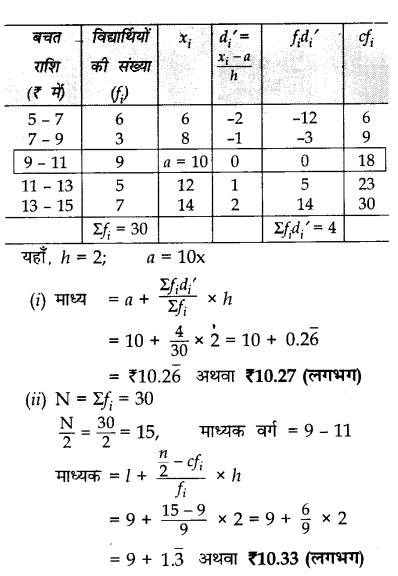
गरीब लड़कियों की मदद के लिए उनकी कक्षा के विद्यार्थियों द्वारा बचाए गए जेबखर्च को निम्नलिखित तालिका द्वारा दर्शाया गया है:

आँकड़ों का माध्य तथा माध्यिका ज्ञात कीजिए।

Question 18.
यदि एक समांतर श्रेढी का सातवां पद \(\frac { 1 }{ 9 }\) है तथा उसके नौंवाँ पद \(\frac { 1 }{ 7 }\) है, तो उसका 63 वाँ पद ज्ञात कीजिए।

Question 19.
यदि बिंदु A(0, 2), बिंदुओं B(3, p) तथा C(p, 5) से समदूरस्थ है, तो p का मान ज्ञात कीजिए। AB की लंबाई भी ज्ञात कीजिए।

Question 20.
यदि बिंदु A(-2, 1), B(a, b) तथा C(4, -1) संरेखी हैं तथा a – b = 1 है तो a तथा b के मान ज्ञात कीजिए।

Question 21.
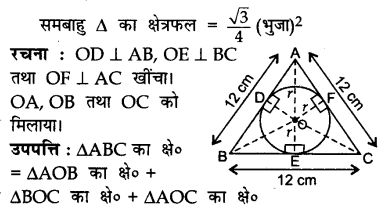
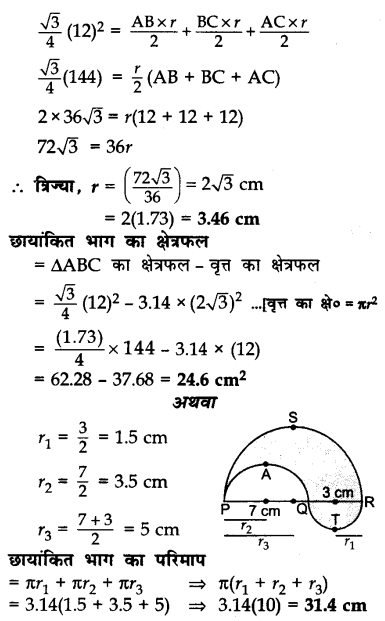
आकृति में, 12 सेमी भुजा वाली एक समबाहु त्रिभुज ABC के अंतर्गत एक वृत्त खींचा गया है जिसका केंद्र O है। अंत:वृत्त की त्रिज्या ज्ञात कीजिए तथा छायांकित भाग को क्षेत्रफल ज्ञात कीजिए। [π = 3.14 तथा √3 = 1.73 लीजिए।]

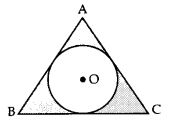
अथवा
आकृति में, PSR, RTQ तथा PAQ तीन अर्द्धवृत्त हैं जिनके व्यास क्रमशः 10 सेमी, 3 सेमी तथा 7 सेमी है। छायांकित भाग का परिमाप ज्ञात कीजिए। [π = 3.14 लीजिए।]

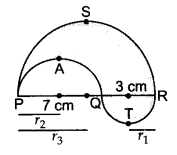
Question 22.
एक किसान अपने खेत में 10 मी व्यास और 2 मी गहरी एक बेलनाकार टंकी को आंतरिक व्यास 20 सेमी व्यास वाले एक पाइप द्वारा नहर से जोड़ता है। यदि पाइप में पानी 4 किमी/घंटा की चाल से बह रहा है तो कितने समय में टंकी पूरी भर जाएगी?
अथवा
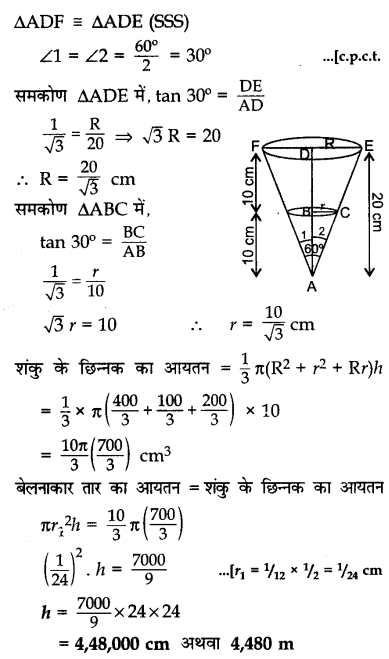
20 सेमी ऊँचाई और 60° शीर्षकोण वाले एक ठोस धातु के लंबवृत्तीय शंकु को उसकी ऊँचाई के बीचों-बीच से होकर जाते एक तल से दो भागों में काटा गया है जबकि तल शंकु के आधार के समांतर है। यदि प्राप्त शंकु के छिन्नक को \(\frac { 1 }{ 12 }\) सेमी व्यास वाले एक तार के रूप में खींचा जाता है, तो तार की लंबाई ज्ञात कीजिए।

SECTION D

प्रश्न संख्या 23 से 30 तक प्रत्येक प्रश्न के 4 अंक हैं।

Question 23.
सीता देवी गली के जानवरों को पेयजल उपलब्ध कराने के उद्देश्य से सड़क के किनारे आयताकार तालाब बनवाना चाहती है। यदि तालाब की लंबाई में 2 फुट की कमी तथा चौड़ाई में 1 फुट की वृद्धि कर दी जाए तो उसका क्षेत्रफल 3 वर्गफुट कम हो जाएगा। यदि इसकी लंबाई में 1 फुट की वृद्धि तथा चौड़ाई में कोई परिवर्तन न किया जाए तो इसका क्षेत्रफल 4 वर्गफुट बढ़ जाएगा। तालाब की लंबाई एवं चौड़ाई ज्ञात कीजिए।
सीता देवी को गली के जानवरों के लिए पेयजल उपलब्ध करवाने के लिए किस बात ने प्रेरित किया?

Question 24.
ΔABC में, लम्ब AD तथा CE एक-दूसरे को बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए:
(i) ΔAPE ~ ΔCPD
(ii) AP x PD = CP x PE
(iii) ΔADB ~ ΔCEB
(iv) AB x CE = BC x AD

Question 25.
सिद्ध कीजिए : (cot A + sec B)² – (tan B – cosec A)² = 2 (cot A . sec B + tan B . cosec A)
अथवा
सिद्ध कीजिए : (sinθ + cosθ + 1) . (sinθ – 1 + cosθ) . secθ . cosecθ = 2

Question 26.
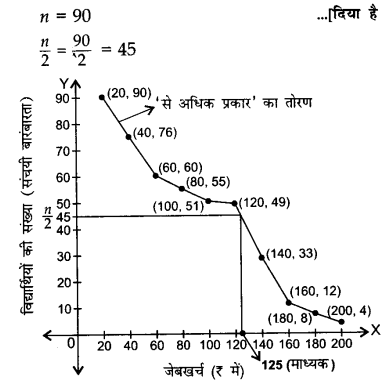
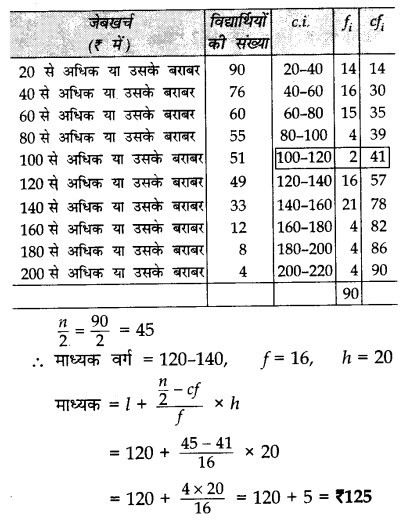
नीचे दी गई बारंबारता सारणी विद्यार्थियों के समूह के द्वारा प्राप्त की गई जेबखर्च की राशि को दर्शाती है:

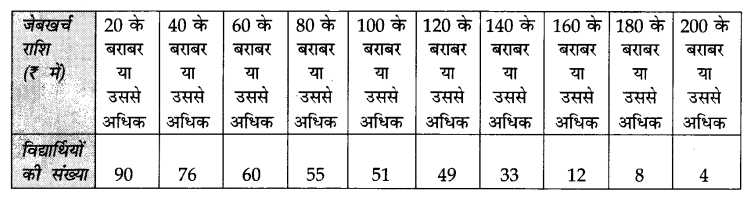
उपरोक्त सारणी से ‘से अधिक प्रकार’ का तोरण बनाइए तथा उससे माध्यिका निकालिए। माध्यिका गणना का सत्यापन कीजिए।

Question 27.
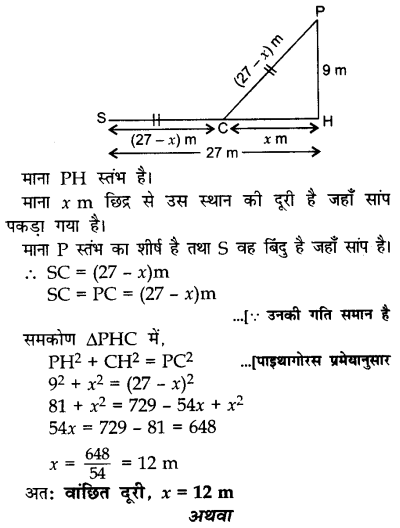
एक मोर एक 9 मी ऊँचे स्तंभ के शिखर पर बैठा है। स्तंभ के तेल से 27 मी की दूरी पर एक सांप स्तंभ के आधार पर स्थित छिद्र की ओर आ रहा है। सांप को देखकर मोर उसकी ओर झपटता है, यदि उन दोनों की गति समान है तो सांप अपने छिद्र से कितनी दूरी पर पकड़ा गया?
अथवा
दो प्राकृत संख्याओं का अंतर 5 है तथा उनके व्युतक्रमों का अंतर \(\frac { 1 }{ 10 }\) है, तो संख्याएँ ज्ञात कीजिए।

Question 28.
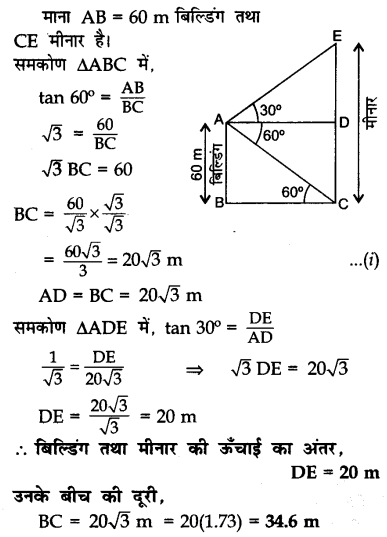
एक 60 मी ऊँची बिल्डिंग के शिखर से एक मीनार के शिखर तथा पाद के उन्नयण कोण तथा अवनमन कोण क्रमश: 30° तथा 60° हैं। बिल्डिंग तथा मीनार की ऊँचाइयों का अंतर तथा उनके बीच की दूरी ज्ञात कीजिए।

Question 29.
एक बैग में कार्ड हैं, जिन पर 1 से 49 तक की संख्याएँ अंकित हैं। इन कार्डों को अच्छी प्रकार से मिलाकर, उनमें से यादृच्छया एक कार्ड निकाला गया। प्रायिकता ज्ञात कीजिए कि निकाले गए कार्ड पर अंकित संख्या:
(i) एक विषम संख्या है।
(ii) 5 का गुणज है।
(iii) एक पूर्ण वर्ग संख्या है।
(iv) एक सम अभाज्य संख्या है।

Question 30.
सुशांत के पास ऊपर से खुला उल्टे शंकु के आकार का एक बरतन है जिसकी ऊँचाई 11 सेमी तथा ऊपरी सिरे की त्रिज्या 2.5 सेमी है। यह बरतन पानी से पूरा भरा हुआ है। इस बरतन में 0.5 सेमी व्यास की धातु की गोलाकार गोलियाँ डाली गईं जिनसे बरतन के पानी का \(\frac { 2 }{ 5 }\) वाँ भाग बाहर आ गया। ज्ञात कीजिए कि इस बरतन में कितनी गोलियाँ डाली गईं। सुशांत ने ऐसा प्रबंध किया कि बरतन से निकली पानी सीधा फूलों की क्यारियों को सींच सके। सुशांत ने इस कार्य से किस मूल्य का प्रदर्शन किया।
अथवा
ऊँचाई 2.8 सेमी और व्यास 4.2 सेमी वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल काट लिया जाता है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [π = \(\frac { 22 }{ 7 }\) लीजिए।]

SOLUTIONS

Solution 1.

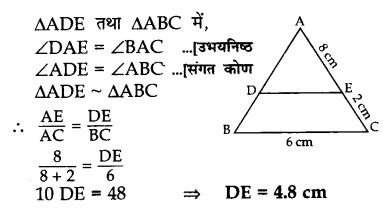
Solution 2.

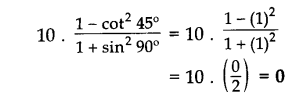
Solution 3.
∠OQP = 90° [वृत्त की स्पर्श रेखाएँ, स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती हैं।]
∠ORP = 90°
∠OQP + ∠QPR + ∠ORP + ∠QOR = 360° …..[चतुर्भुज के चारों कोणों का योग गुणधर्म]
90° + 46° + 90° + ∠QOR = 360°
∠QOR = 360° – 90° – 46° – 90° = 134°

Solution 4.
दो पासे फेंकने पर कुल परिणाम = 6 x 6 = 36
दोनों पासों पर संख्या प्राप्त करने के संभावित परिणाम
{(2,2), (2,4), (2,6) {(4,2), (4,4), (4,6)}, (6,2), (6,4), (6,6)}
अर्थात्, 9
P(सम संख्या) = \(\frac { 9 }{ 36 }\) = \(\frac { 1 }{ 4 }\)

Solution 5.

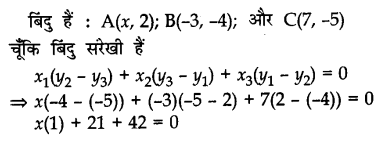
x + 63 = 0
x = -63

Solution 6.

Solution 7.

Solution 8.

Solution 9.

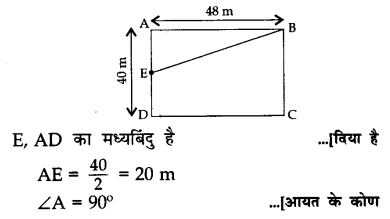
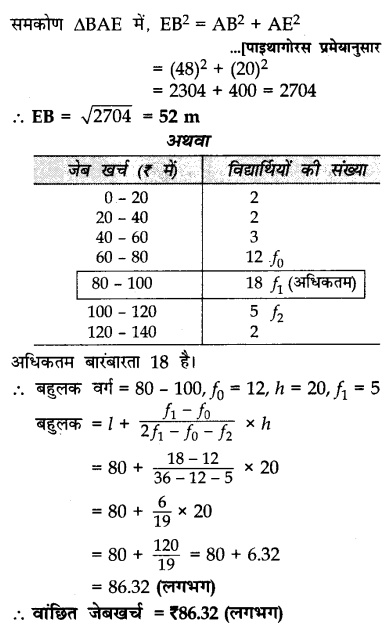
Solution 10.

Solution 11.

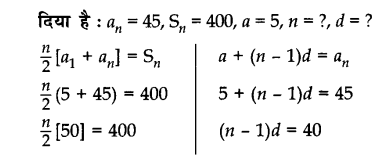
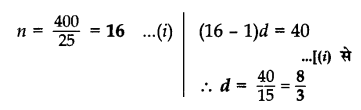
Solution 12.
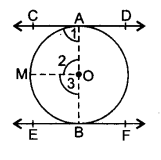
दिया है : CD और EF, । हैं एक केन्द्र O वाले वृत्त के दो बिंदु A तथा B पर समांतर स्पर्श रेखाएँ हैं।
सिद्ध करना है: AB, केन्द्र O से गुजरने वाली रेखा है अथवा AOB वृत्त का व्यास है।
रचना : OA तथा OB को मिलाया। OM || CD खींचा।
उपपत्ति : ∠1 = 90° …(i) [वृत्त की स्पर्श रेखा स्पर्श बिंदु से पाने वाली त्रिज्या पर लंब होती है।]
OM || CD
∠1 + ∠2 = 180° …[एक ही ओर बने कोण]
90° + ∠2 = 180° …[(1) से]
∠2 = 180° – 90° = 90°
इसी प्रकार, ∠3 = 90°
∠2 + ∠3 = 90° + 90° = 180°
AOB एक सरल रेखा है।
अतः O केन्द्र वाले वृत्त पर AOB एक व्यास है।
AB केन्द्र O से गुजरता है।

Solution 13.

Solution 14.
माना पत्नी की मासिक आय = ₹ x
तब आदमी की मासिक आय = ₹ (x + 600)

Solution 15.

Solution 16.

Solution 17.

Solution 18.

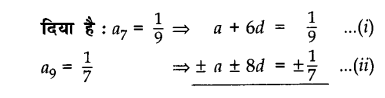
Solution 19.

Solution 20.

Solution 21.

Solution 22.

Solution 23.

Solution 24.

Solution 25.

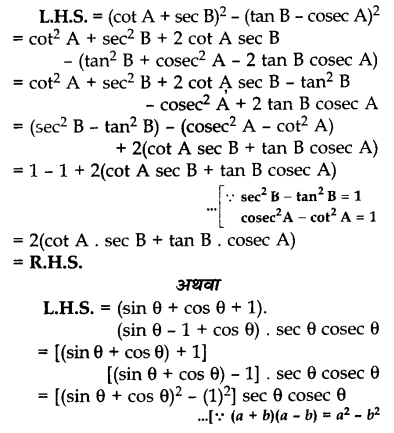
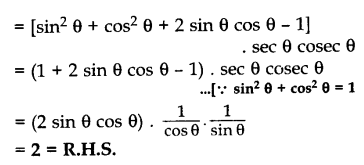
Solution 26.

Solution 27.

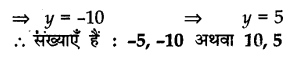
Solution 28.

Solution 29.

Solution 30.

We hope the CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 4 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths in Hindi Medium Paper 4, drop a comment below and we will get back to you at the earliest.