CBSE Sample Papers for Class 10 Maths Paper 1 is part of CBSE Sample Papers for Class 10 Maths Here we have given CBSE Sample Papers for Class 10 Maths Paper 1. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.
CBSE Sample Papers for Class 10 Maths Paper 1
| Board | CBSE |
| Class | X |
| Subject | Maths |
| Sample Paper Set | Paper 1 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 1 of Solved CBSE Sample Papers for Class 10 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 80
GENERAL INSTRUCTIONS:
- All questions are compulsory.
- This question paper consists of 30 questions divided into four sections A, B, C and D.
- Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions 1 of 4 marks each.
- There is no overall choice. However, internal choice has been provided in one question of 2 marks, 1 three questions of 3 marks each and two questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
- In question of construction, drawings shall be neat and exactly as per the given measurements.
- Use of calculators is not permitted. However, you may ask for mathematical tables.
SECTION A
Question numbers 1 to 6 carry 1 mark each.
Question 1.
Given that LCM (91, 26) = 182, find HCF (91, 26).
Question 2.
Does the rational number \(\frac { 441 }{ { 2 }^{ 2 }.{ 5 }^{ 7 }.{ 7 }^{ 2 } } \) has a terminating or a non-terminating decimal representation?
Question 3.
If 1 is a zero of the polynomial p(x) = ax² – 3 (a – 1) x – 1, then find the value of a.
Question 4.
The nth turn of an AP is 7 – 4n. Find its common difference.
Question 5.
If adjoining figure, DE || BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
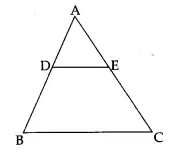
Question 6.
In adjoining figure, PA and PB are tangents to the circle drawn an external point P. CD is a third tangent touching the circle at PB = 10 cm and CQ = 2 cm, what is the length of PC?
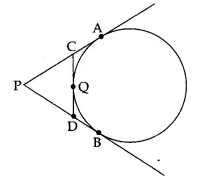
SECTION B
Question numbers 7 to 12 carry 2 marks each.
Question 7.
Determine the values of m and n, so that the following system of linear equations has infinite number of solutions:
(2m – 1)x + 3y – 5; 3x + (n – 1)y – 2 = 0.
Question 8.
Find the roots of the quadratic equation: 4 √3 x² + 5x – 2 √3 =0.
Question 9.
A bag contains 5 red, 8 green and 7 white balls. One ball is drawn at random from the bag. Find the probability of getting:
(i) a white ball or a green ball.
(ii) neither a green ball nor a red ball.
Question 10.
Without using trigonometric tables, find the value of
\(\frac { cos{ 70 }^{ o } }{ sin{ 20 }^{ o } } \) + cos 57° . cosec 33° – 2 cos 60°.
Question 11.
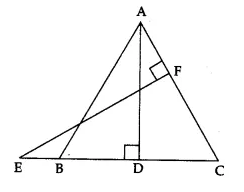
In the adjoining figure, E is a point on the side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC,
prove that: AB x EF = AD x EC.
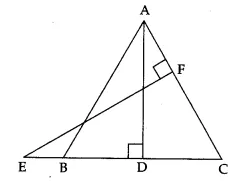
Question 12.
Two circles touch externally. The sum of their areas is 58π cm² and the distance between their centres is 10 cm. Find the radii of the two circles.
SECTION C
Question numbers 13 to 22 carry 3 marks each.
Question 13.
Prove that

Question 14.
Prove that: (1 + cot A – cosec A) (1 + tan A + sec A) = 2.
Question 15.
Solve the following pair of linear equations:
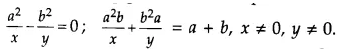
OR
The sum of the numerator and denominator of a fraction is 4 more than twice the numerator. If the numerator and denominator both increased by 3, they are in the ratio 2 : 3. Determine the fraction.
Question 16.
Show that \(\frac { 1 }{ 2 }\) and \(\frac { -3 }{ 2 }\) are the zeroes of the polynomial 4x² + 4x – 3 and verify the relationship between zeroes and coefficients of the polynomial.
OR
Quadratic polynomial 2x² – 3x + 1 has zeroes as α and β. Form a quadratic polynomial whose zeroes are 3α and 3β.
Question 17.
Construct a ∆ABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°, then construct a triangle similar to the given triangle whose sides are \(\frac { 6 }{ 5 }\) of the corresponding sides of the ∆ABC.
Question 18.
Find the values of k if the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear. .
OR
If P(9a – 2, -b) divides the line segment joining A(3a + 1, -3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
Question 19.
Prove that the points A (-3, 0), B (1, – 3) and C(4, 1) are the vertices of an isosceles right triangle.
Question 20.
Cards marked with all 2-digit numbers are placed in a box and are mixed thoroughly. One card is drawn at random. Find the probability that the number on the card is
(i) divisible by 10
(ii) a perfect square number
(iii) a prime number less than 25.
OR
The king, queen and jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards. Find the probability of getting a card of
(i) hearts
(ii) queen
(iii) clubs.
Question 21.
Find the median of the following data:

Question 22.
The following frequency distribution shows the number of rims scored by some batsmen of India in one-day cricket matches:

Find the mode for the above data.
SECTION D
Question numbers 23 to 30 carry 4 marks each.
Question 23.
Prove that n³ – n is divisible by 6 for every positive integer n.
Question 24.
A sum of Rs 1600 is to be used to give 10 cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.
What is the importance of an academic prize in student’s life?
Question 25.
A motor boat whose speed is 20 km/h in still water takes 1 hour more to go 48 km upstream than to return downstream to the same spot. Find the speed of the stream.
OR
A shopkeeper buys some books for Rs 80. If he had bought 4 more books for the same amount, each book would have cost Rs 1 less. Find the number o.f books he bought.
Question 26.
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Question 27.
In the adjoining figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
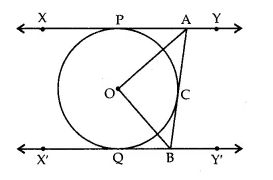
OR
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
Question 28.
The angles of elevation of the top of a tower from two points P and Q at distances of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab .
OR
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
Question 29.
In the adjoining figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find
(i) the area of the shaded region.
(ii) the perimeter of the shaded region.
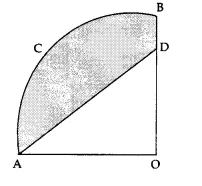
Question 30.
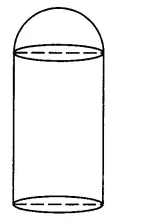
A building is in the form of cylinder surmounted by a hemispherical dome (shown in the adjoining figure). The base diameter of the dome is equal to \(\frac { 2 }{ 3 }\) of the total height of the building. Find the height of the building if it contains \(67\frac { 1 }{ 21 }\) m³ of air.
Answers
Answer 1.
∵ HCF x LCM = 91 x 26
⇒HCF x 182 = 91 x 26
⇒HCF = \(\frac { 91X26 }{ 182 }\) = 13.
Answer 2.
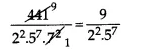
Now numerator and denominator are co-prime and denominator is of the form 2m x 5n. Hence, given rational number is terminating.
Answer 3.
Given 1 is a zero of p(x) = ax² – 3 (a – 1) x – 1
⇒ p(1) = 0 ⇒ a x 1² – 3(a – 1) x 1 – 1 = 0
⇒ a – 3a + 3 – 1 = 0
⇒ – 2a = – 2 ⇒ a = 1
Answer 4.
Given an = 7 – 4n ⇒a2 = 7 – 4 x 2 = -1 and a1 = 7 – 4 x 1 = 3
∴ common difference d = a2 – a1 = -1 – 3 = -4
Answer 5.
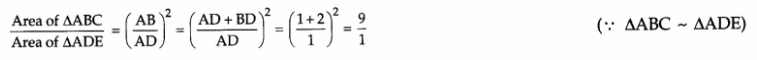
Area of ∆ABC : Area of ∆ADE = 9:1
Answer 6.
PC = PA – CA = PB – CQ = (10 – 2) cm = 8 cm (∵ PA = PB and CA = CQ)
Answer 7.
For infinite number of solutions
\(\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { { c }_{ 1 } }{ { c }_{ 2 } } \)
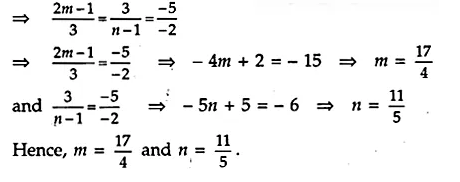
Answer 8.
4√3 x² + 5x – 2√3 = 0
=> 4√3 x² + 8x – 3x – 2√3 = 0
=> 4x(√3x + 2) – √3(√3x + 2) = 0
=> (√3x + 2) (4x – √3 ) = 0
=> √3x + 2 = 0 or 4x – √3 = 0
\(x=-\frac { 2 }{ \sqrt { 3 } } or\frac { \sqrt { 3 } }{ 4 } \)
Answer 9.
Total number of possible outcomes = 5 + 8 + 7 = 20
(i) Number of favourable outcomes = number of white balls or number of green balls
= 7 + 8 = 15
∴ P (a white or a green ball) = \(\frac { 15 }{ 20 } =\frac { 3 }{ 4 } \)
(ii) Number of favourable outcomes = number of white balls = 7
∴ P (neither green nor red ball) = \(\frac { 7 }{ 20 }\)
Answer 10.
\(\frac { cos{ 70 }^{ o } }{ sin{ 20 }^{ o } } \) + cos 57° . cosec 33° – 2 cos 60°.
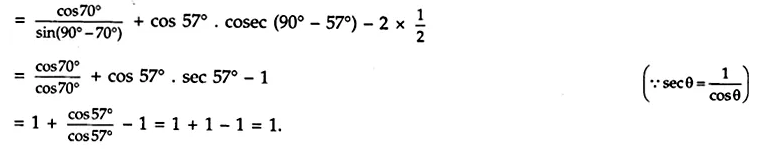
Answer 11.
Given, ∆ABC is an isosceles triangle with AB = AC.
⇒ ∠C = ∠B (angles opp. equal sides of a ∆ are equal)
In ∆ABD and ∆ECF,
∠ABD = ∠ECF (∵ ∠B = ∠C, proved above)
and ∠ADB = ∠EFC (each = 90°)
∴ ∆ABD ~ ∆ECF (by AA similarity criterion)
∴ \(\frac { AB }{ EC } =\frac { AD }{ EF } \) ⇒ AB x EF = AD x EC, as required.
Answer 12.
Let r1 cm and r2 cm be the radii of two circles, then
r1 + r2 = 10 ….(i)
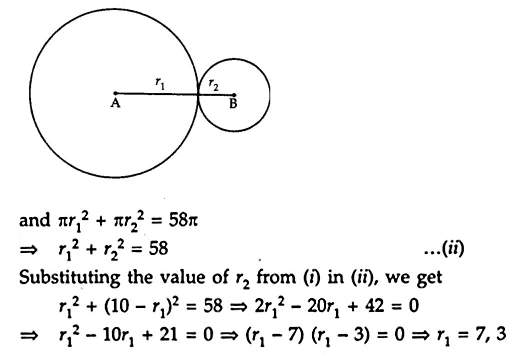
If r1 = 7, then r2 = 3 and if r1 = 3, then r2 = 7.
Hence, the radii of two circles are 7 cm and 3 cm.
Answer 13.
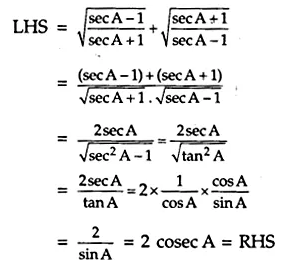
Answer 14.
(1 + cot A – cosec A) (1 + tan A + sec A)
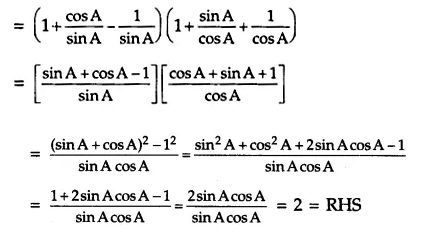
Answer 15.
Given
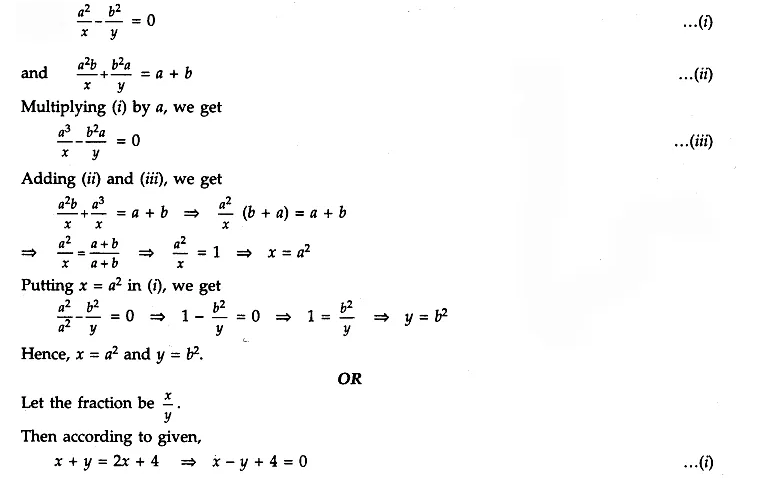
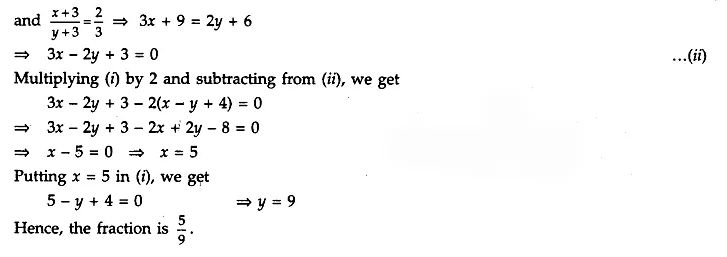
Answer 16.
Let f(x) = 4x² + 4x – 3, then


Answer 17.
Steps of construction:
1. Draw AB = 5 cm.
2. At the point A draw ∠BAX = 45°.
3. From AX cut off AC = 6 cm.
4. Join BC. ∆ABC is formed with given data.
5. Draw \(\overrightarrow { AL } \) making acute angle with AB as shown in the figure.
6. Draw 6 arcs at P1 P2, P3, P4, P5 and P6 such that AP1 = P1P2 = P2P3 = P3P4 = P4P5 = P5P6.
7. Join BP5.
8. Draw B’P6 || BP5 meeting AB produced at B’.
9. From B’, draw B’C’ || BC meeting AX at C’.
∆AB’C’ ~ ∆ABC.
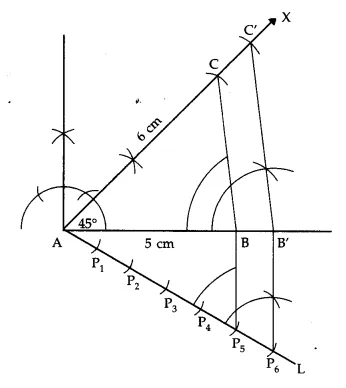
Answer 18.
Since the given points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear, the area of triangle formed by them is zero

Answer 19.
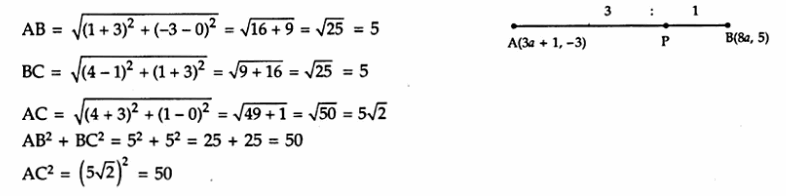
∴AB² + BC² = AC² and AB = BC
Hence ABC is a right angled isosceles triangle , right angled at B
Answer 20.
Cards have numbers 10 to 99 (both inclusive) i.e. 10, 11, 12, … 99.
∴ Total number of cards = 90 (99 – 9 = 90)
(i) The numbers from 10 to 99 which are divisible by 10 are 10, 20, 30, …, 90
The number of’such numbers = 9.
∴ Required probability = \(\frac { 9 }{ 90 } =\frac { 1 }{ 10 } \)
(ii) The numbers from 10 to 99 which are perfect squares are 16, 25, 36, 49, 64, 81.
The number of such numbers = 6.
∴ Required probability = \(\frac { 6 }{ 90 } =\frac { 1 }{ 15 } \)
(iii) The numbers from 10 to 99 which are prime numbers less than 25 are 11, 13, 17, 19, 23.
The number of such numbers = 5.
∴ Required probability = \(\frac { 5 }{ 90 } =\frac { 1 }{ 18 } \)
OR
After removing king, queen and jack of clubs, the number of cards left = 49
(i) The number of cards of hearts left in the remaining cards = 13
∴ P (a card of hearts) = \(\frac { 13 }{ 49 }\)
(ii) The number of cards of queens left in the remaining cards = 13
∴ P (a card of queen) = \(\frac { 3 }{ 49 }\)
(iii) The number of cards of clubs left in the remaining cards = 10
∴ P (a card of clubs) = \(\frac { 10 }{ 49 }\)
Answer 21.

Answer 22.
The maximum class frequency is 10 and the class corresponding to this frequency is 6000 – 8000. So, the modal class is 6000 – 8000.
Here, l = 6000, h = 2000, f1 = 10, f0 = 8 and f2 = 2
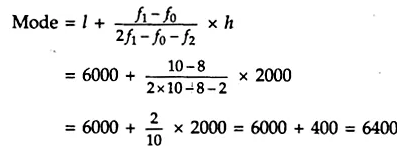
∴ Mode = 6400
Answer 23.
Given n is any positive integer. Applying Euclid’s lemma with divisor = 6, we get
n = 6q, 6q + 1, 6q + 2, 6q + 3, 6q + 4 or 6q + 5, where q is some whole number.
Six cases arise.
Case I.
If n = 6q, then
n3 – n = n(n – 1) (n + 1) = 6q(6q – 1 )(6q + 1), which is divisible by 6.
Case II.
If n = 6q + 1, then
n3 – n = n(n – 1 )(n + 1) = (6q + 1)(6q)(6q + 2)
= 12q(6q + 1)(3q + 1), which is divisible by 6.
Case III.
If n = 6q + 2, then
n3 – n – n(n – 1 )(n + 1) = (6q + 2)(6q + 1)(6q + 3)
= 6(3q + 1)(6q + 1)(2q + 1), which is divisible by 6.
Case IV.
If n – 6q + 3, then
n3 – n = n(n – 1 )(n + 1) = (6q + 3)(6q + 2)(6q + 4)
= 12(2q + 1)(3q + 1)(3q + 2), which is divisible by 6.
Case V.
If n = 6q + 4, then
n3 – n = n(n – 1 )(n + 1) = (6q + 4)(6q + 3)(6q + 5)
= 6(3q + 2)(2q + 1)(6q + 5), which is divisible by 6.
Case VI.
If n = 6q + 5, then
n3 – n = n(n – 1 )(n + 1) = (6q + 5)(6q + 4)(6q + 6)
= 12(69 + 5)(3q + 2)(q + 1), which is divisible by 6.
Thus, in all cases, n3 – n is divisible by 6.
Hence, for every positive integer n, n3 – n is divisible by 6.
Answer 24.
Let the first cash prize be Rs x.
It is given that each prize is Rs 20 less than its preceding prize.
These cash prizes form an AP with a = x, d = – 20, Sn = 1600 and n = 10.
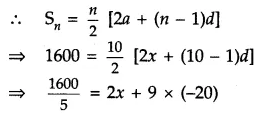
⇒ 320 = 2x – 180
⇒ 2x = 500
⇒ x = 250.
Therefore, the prizes are 250, 250 – 20, 250 – 2 × 20, 250 – 3 × 20, 250 – 4 × 20, 250 – 5 × 20,
i.e., 250, 230, 210, 190, 170, 150, 130, 110, 90, 70
Hence, the values of cash prizes are
Rs 250, Rs 230, Rs 210, Rs 190, Rs 170, Rs 150, Rs 130, Rs 110, Rs 90 and Rs 70.
Academic prize generates spirit of competition. One starts doing hard work which leads to success.
Answer 25.
Let the speed of the stream be x km/h.
Given, speed of the motor boat in still water = 20 km/h.
Then, the speed of the boat upstream = (20 – x) km/h
and the speed of the bpat downstream = (20 + x) km/h
Time taken by the motor boat to cover 48 km upstream = \(\frac { 48 }{ 20-x }\) hours,
time taken by the motor boat to cover 48 km downstream = \(\frac { 48 }{ 20+x }\) hours.
According to given, \(\frac { 48 }{ 20-x }\) – \(\frac { 48 }{ 20+x }\) = 1
⇒ 48(20 + x) – 48(20 – x) = (20 – x) (20 + x) ⇒ 48(2x) = 20² – x²
⇒ x² + 96x – 400 = 0
⇒ (x – 4) (x + 100) = 0
⇒ x = A or x = – 100 but x being the speed of the stream cannot be negative
⇒ x = 4
Hence, the speed of the stream is 4 km/h.
OR
Let the number of books the shopkeeper bought be x.
Given, total cost of books = Rs 80
Then cost of one book = \(\frac { 80 }{ x }\)
When he had bought 4 more books for same amount i.e. Rs 80, then cost of one book = \(\frac { 80 }{ x+4 }\)
According to given \(\frac { 80 }{ x }\) – \(\frac { 80 }{ x+4 }\) = 1
⇒ 80(x + 4) – 80x = x(x + 4)
⇒ 320 = x² + 4x
⇒ x² + 4x – 320 = 0
⇒(x + 20) (x- 16) = 0
⇒ x = 16 or x = – 20 but x being the number of books cannot be negative
⇒ x = 16
Hence, the number of books he bought = 16.
Answer 26.
Given. ABC is a right triangle right angled at A so that BC is its hypotenuse.
To prove. BC² = AB² + AC².
Construction. From A, draw AD ⊥ BC.
Proof. In ∆DBA and ∆ABC,
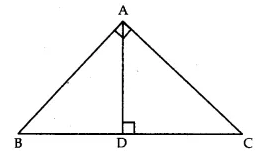
∠ABD = ∠ABC (same angle)
and ∠ADB = ∠BAC (each = 90°)
∴ ∆DBA ~ ∆ABC (AA similarity criterion)
\(\frac { AB }{ BC } =\frac { BD }{ AB } \) => AB² = BD x BC …(i)
In ∆DAC and ∆ABC,
∠ACD = ∠ACB (same angle)
and ∠ADC = ∠BAC (each = 90°)
∴ ∆DAC ~ ∆ABC (AA similarity criterion)
\(\frac { AC }{ BC } =\frac { DC }{ AC } \) => AC² = DC x BC …(ii)
On adding (i) and (ii), we get
AB² + AC² = BD x BC + DC x BC
= (BD + DC) x BC = BC x BC
=> AB² + AC² = BC².
Hence, BC² = AB² + AC².
Answer 27.
Join OP, OQ and OC. Mark the angles as shown in the figure.
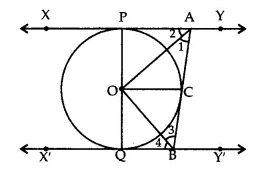
In ∆OAC and ∆OAP,
OA = OA (common)
OC = OP (radii of some circle)
AC = AP (tangent drawn from A)
∴ ∆OAC ≅ ∆OAP (by SSS rule of congruency)
∴∠1 = ∠2 => ∠PAC = 2∠1 …(i)
Similarly,
∴∆OBC ≅ ∆OBQ,
∴ ∠3 = ∠4 => ∠QBC = 2∠3 …(ii)
As XY || X’Y’ and AB is a transversal,
∠PAC + ∠QBC = 180° (sum of co-int ∠S)
=> 2∠1 + 2∠3 = 180° [using (i) and (ii)]
=> ∠1 + ∠3 = 90° …(iii)
In ∆OAB, ∠AOB + ∠1 + ∠3 = 180° (sum of angles of a ∆)
=> ∠AOB + 90° = 180° (using (iii))
=> ∠AOB = 90°.
OR
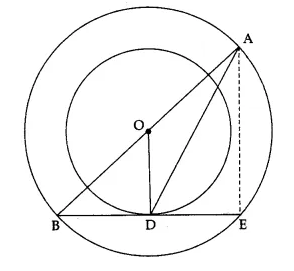
Let the line BD meet the bigger circle at E. Join AE. Let O be the centre of two concentric circles.
As AB is a diameter of the bigger circle, O is mid-point of AB.
BD is tangent to the smaller circle and OD is radius of smaller circle through the point of contact D, OD ⊥ BE.
Since BE is a chord of the bigger circle and OD ⊥ BE,
BD = DE
(∵ Perpendicular from the centre to a chord bisects it)
=> D is mid-point of BE
∴ OD = \(\frac { 1 }{ 2 }AE\)
(∵ Segment joining the mid-points of any two sides of a triangle is half of the third side)
=> AE = 2 OD => AE = (2 x 8) cm = 16 cm (∵ OD = 8 cm)
In ∆OBD; ∠ODB = 90°, by Pythagoras theorem, we get
OB² = BD² + OD² => 13² = BD² + 8² (∵ OB is radius of bigger circle, so OB = 13 cm)
=> BD² = 169 – 64 = 105 => BD = √105 cm
But DE = BD => DE = √105 cm
Now ∠AEB = 90° (∵ angle in a semicircle = 90°)
=> ∠AED = 90°
In ∆ADE; ∠AED = 90°, by Pythagoras theorem, we get
AD² = AE² + DE² => AD² = 16² + (√105)² = 256 + 105 = 361
=> AD = √361 cm => AD = 19 cm
Answer 28.
Let AB be the tower of height h (units).
AP = a, QA = b.
As the angles of elevation are complementary, if ∠APB = θ° then ∠AQB = 90° – θ°
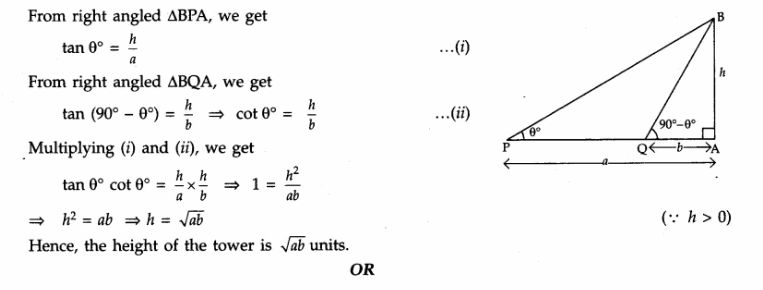
Let CD be a vertical tower of height h metres. From a point A on the ground, the angle of elevation of the top is 60°. B is another point 10 m vertically above A and angle of elevation of the top of the tower from B is 45°.
Let AC = d metres
From B, draw BE ⊥ CD.
Then BE = AC and EC = BA = 10 m.
From right angled ∆ADC, we get

Answer 29.
(i) Radius of the circle = 3.5 cm = \(\frac { 7 }{ 2 }\)
∴ Area of the quadrant OACB = \(\frac { 1 }{ 4 }\) x πr²

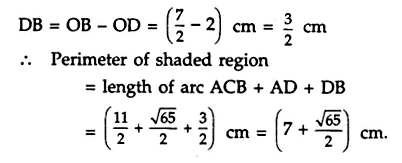
Answer 30.
Let the radius of the spherical dome be r metres and the total height of the building be h metres.
Since the base diameter of the dome is \(\frac { 2 }{ 3 }\) of the total height of the building, therefore,
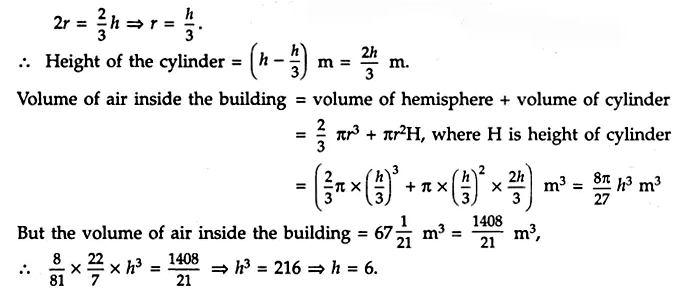
Hence , the height of the building = 6 m
We hope the CBSE Sample Papers for Class 10 Maths Paper 1 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths Paper 1, drop a comment below and we will get back to you at the earliest.