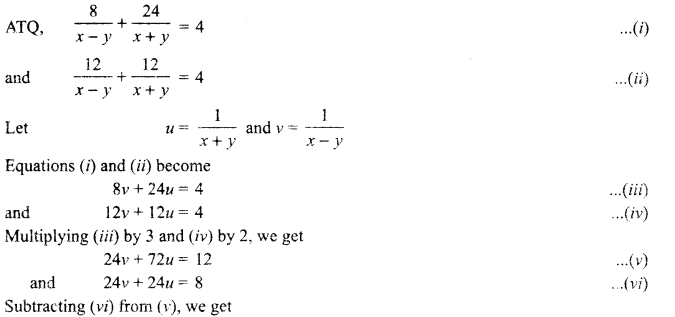Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 1 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Set 1 with Solutions
Time: 3 Hours
Maximum Marks: 80
General Instructions:
1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.
Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Section-I
Section 1 has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
Question 1.
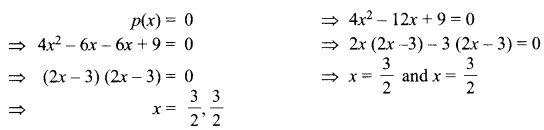
Find the zeroes of the of the polynomials p(x) = 4x2 – 12x + 9
Solution :
Question 2.
In the given figure, DE || BC. Find \(\frac{x}{y}\) DE || BC
Solution :
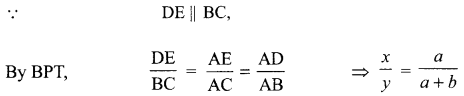
Question 3.
If 2k + 1, 6, 3& + 1 are in AP, then find the value of k.
OR
If the sum of n terms of an AP is 2n2 + 5n, then find the 2nd term
Solution :
For an AP a, b, c; 2b = a + c ⇒ (2k + 1) + (3k + 1) = 2×6
5k+2=12
⇒ 5k = 10
⇒ k = 2
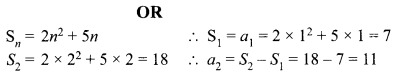
Question 4.
If x = a, y = b is the solution of the pair of equations x-y-2 and x + y = 4, then find the values of a and b.
Solution :
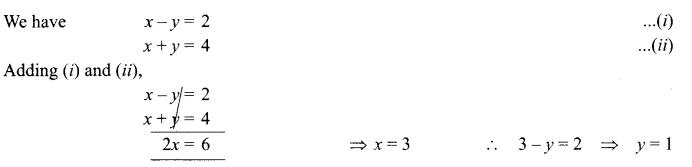
Question 5.
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle (see figure). Find the length of the chord CD parallel to XY and at a distance 8 cm from A.
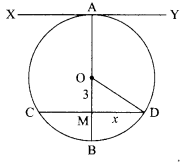
Solution :
OD2 = OM2 + DM2
⇒ 52 = 32 + x2
x2 = 25 – 9 = 16
x = 4
CD =2 x = 2 × 4 = 8 cm
Question 6.
Find the radius of the largest right circular cone that can be cut out from a cube of edge 4.2 cm.
Solution :
Edge of the cube = 4.2 cm
∴ Radius of the largest right circular cone \(\frac{1}{2}\) (Edge of the Square) \(=\frac{4.2}{2}=2.1 \mathrm{~cm}\)
Question 7.
The circumference of a circle exceeds its diameter by 180 cm. Find its radius
Solution :
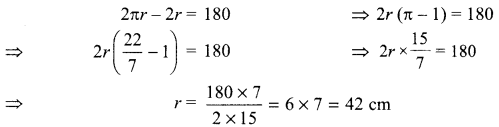
Question 8.
A bag contains 40 balls out of which some are red, some are blue and remaining are black. If the probability of drawing a red ball is \(\frac{11}{20} \) and that of blue ball is \(\frac{1}{5} \) , then find the number of black balls.
OR
Rahim tosses two different coins simultaneously. Find the probability of getting at least one tail.
Solution :
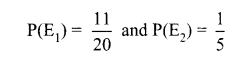
Let the number of black balls = x.
Total number of balls = Total possible outcomes = 40
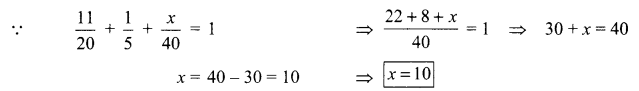
⇒ Number of black balls =10
OR
Number of possible outcomes = 4 as possible outcomes are HH, HT, TH, TT. Favourable outcomes for getting at least one tail are HT, TH, TT No. of favourable outcomes = 3
∴ P(getting at least one tail) =\(\frac{3}{4}\)
Question 9.
If Cos θ \(\frac{7}{8}\) then find the value of \(\frac{(1+\cos \theta)(1-\cos \theta)}{(1-\sin \theta)(1+\sin \theta)}\)
Solution :
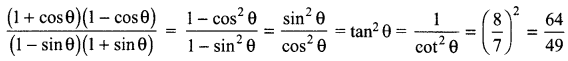
Question 10.
Write whether the rational number \(\frac{7}{75}\) will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
OR
Write the HCF of the smallest composite number and the smallest prime number.
Solution :
\(\frac{7}{75}=0.0933333 \ldots \ldots=0.09 \overline{3}\)
So, it is a non-terminating repeating decimal expansion.
OR
The smallest composite number is 4 and the smallest prime number is 2.
The prime factorisation of 4 = 2 x 2 = 22 and the prime factorisation of 2 = 21
Now, the HCF of 2 and 4 is the product of smallest power of each common prime factor in . the numbers.
HCF (2, 4) = 21 = 2
Question 11.
Find the value(s) of k, if the quadratic equation 3x2 – k √3x + 4 = 0 has equal roots.
OR
If -5 is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p(x2 + x) + k = 0 has equal roots, then find the value of k.
Solution :
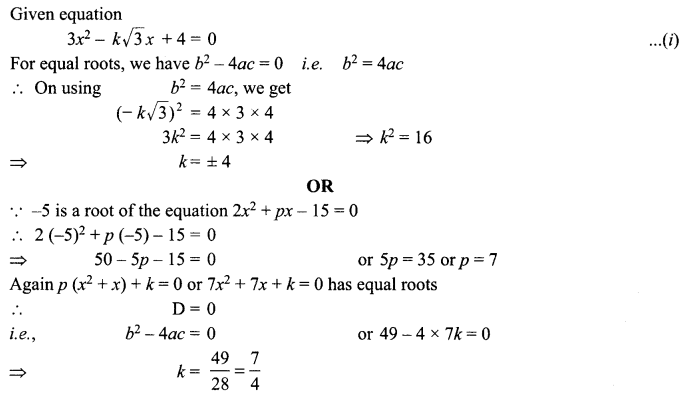
Question 12.
In the given figure, ABCD is a rectangle. Find the values of x and y.
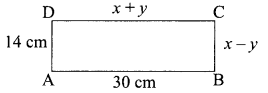
Solution :
Question 13.
If ax2 + bx + c = 0 has equal roots, find the value of
Solution :
For equal roots D = 0
i.e., b2 – 4ac =0
⇒ b2 = 4ac
\(c=\frac{b^{2}}{4 a}\)
Question 14.
In the given figure, PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PA = 15 cm, find the perimeter of APCD.
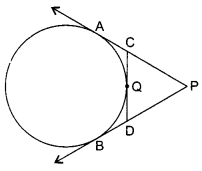
OR
In the given figure, the quadrilateral PQRS circumscribes a circle with centre O. If ∠POQ = 115°, then find ∠ROS.
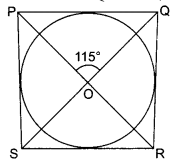
Solution :
Since PA and PB are tangents from same external point P.
PA = PB = 15 cm
Now, Perimeter of APCD = PC + CD + DP = PC + CQ + QD + DP
= PC + CA + DB + DP = PA + PB = 15 cm +15 cm = 30 cm
OR
Solution :
Since ∠POQ = ∠ROS (Vertically opposite angles)
⇒ ∠ROS = 115°
Question 15.
To divide a line segment AB in the ratio 5 : 7, first a ray AX is drawn such that ∠BAX is an acute angle and then at equal distances points are marked on the ray. Find the minimum number of these points.
Solution :
Since 5+ 7 = 12
So, the number of points marked on ray AX = 12.
Question 16.
Find the value of (sin 30° + cos 60°).
Solution :
sin 30° + cos 60° \(=\frac{1}{2}+\frac{1}{2}=\)
Section-II
Question 17.
Case Study Based-1
Medicinal Garden
A medicinal garden is a garden in which different kinds of medicinal plants, like Aloe Vera, Mint, Lemon Balm, etc. are planted with the goal of serving the need of general health maintenance. Observe the following diagram.
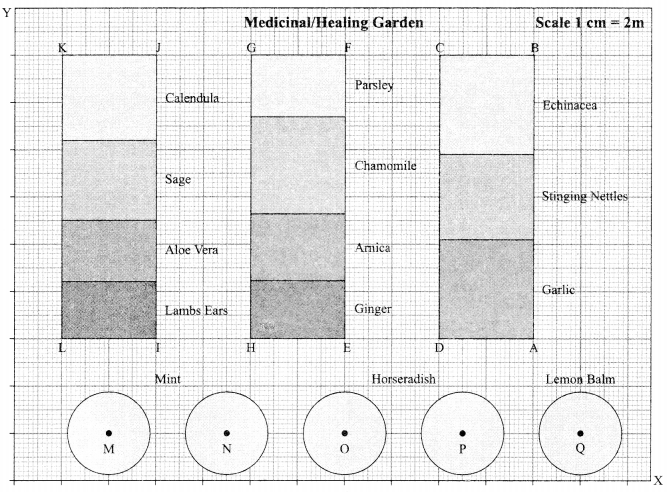
Refer to IJKL
(a) The mid-point of the segment joining the points 1(6, 6) and J(6, 18) is
(i) (7,9)
(ii) \(\left(12, \frac{11}{2}\right) \)
(iii) (6, 12)
(iv) (12,24)
Refer to EFGH
(b) The distance between points H(10, 6) and F(14, 18) is
(i) \(8 \sqrt{5}\)unit
(ii) \(4 \sqrt{10}\) unit
(iii) 18 unit
(iv) 24 unit
Refer to ABCD
(c) The coordinates of the points A and B are (22,6) and (22,18) respectively. The x-coordinate of a point R on the line segment AB such that \(\frac{A R}{A B}=\frac{3}{5}\) is…………….
(i) 18
(ii) 24
(iii) 22
(iv) 31
Refer to MQ
(d) The ratio in which the points (20, k) divides the line segment joining the points M(4, 2) and Q(24, 2) is
(i) 4 : 1
(ii) 16 : 15
(iii) 8 : 21
(iv) 10 : 17
Refer to MH and HP
How much longer is HP than MH given that coordinates of H(10, 6), M(4, 2) and P(19,2)
(i) \((\sqrt{95}-2 \sqrt{3}) \text { unit }\)
(ii) \((\sqrt{97}-2 \sqrt{13}) \text { unit }\)
(iii) \((\sqrt{61}-4 \sqrt{5}) \text { unit }\)
(iv) None of there.
Solution:


Question 18.
Case Study Based-2
A Frame House
A frame-house is a house constructed from a wooden skeleton, typically covered with timber board. The concept of similar triangles is used to construct it. Look at the following picture:

Refer to House (i)
(a) The front view of house (7) is shown below in which point P on AB is joined with point Q
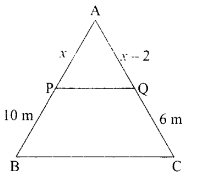
If PQ || BC, AP = x m PB = 10 m. AQ = (x – 2) m, QC = 6 m, then the value of a is
(i) 3m
(ii) 4m
(iii) 5m
(iv) 8 m
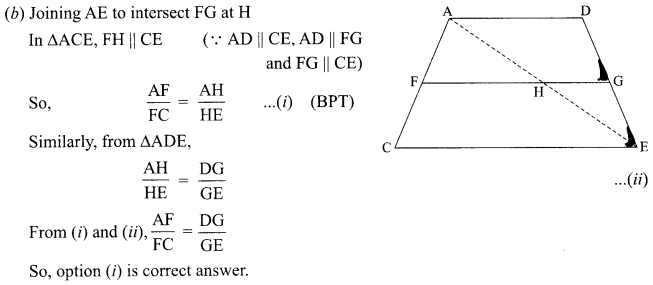
(b) The side vies of house (i) is shown below in which point F on AC is joined with point G on DE.
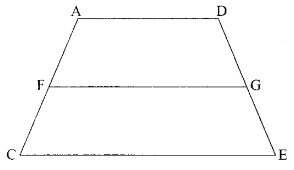
If ACED is a trapezium with AD || CE, F and G are points on non-parallel sides AC and AF
DE respectively such that FG is parallel to AD, then =\(\frac{\mathrm{AF}}{\mathrm{FC}}=\)
(i) \(\frac{\mathrm{DG}}{\mathrm{GE}}\)
(ii) \(\frac{\mathrm{AD}}{\mathrm{CE}}\)
(iii) \(\frac{\mathrm{AF}}{\mathrm{GE}}\)
(iv) \(\frac{\mathrm{DG}}{\mathrm{FC}}\)
(c) The front view of house (ii) is shown below in which point S on PQ is joined with point T on PR.
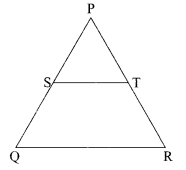
\(\frac{\mathrm{PS}}{\mathrm{QS}}=\frac{\mathrm{PT}}{\mathrm{TR}} \text { and } \angle \mathrm{PST}=70^{\circ}, \angle \mathrm{QPR}=50^{\circ}\) then the angle ∠QRP =
(i) 70°
(ii) 50°
(iii) 80°
(iv) 60°
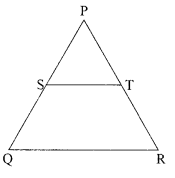
(d) Again consider the front view of house (ii). If S and T are points on side PQ and PR respectively such that
ST || QR and PS : SQ = 3 : 1. Also TP = 6.6 m, then PR is
(i) 6.9 m
(ii) 8.8 m
(iii) 10.5m
(iv) 9.4 m
(e) Sneha has also a frame house whose front view is shown below
If MN || AB, BC = 7.5 m, AM = 4 m and MC = 2 m, then length of BN is
(i) 5 m
(ii) 4 m
(iii) 8 m
(iv) 9 m
Solution :
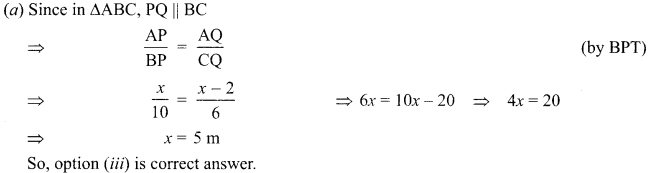

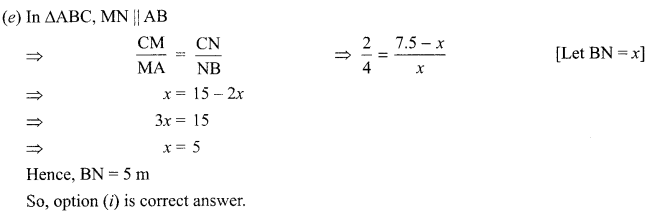
Question 19.
Case Study Based-3

Rainbow is an arch of colours that is visible in the sky, caused by the refraction and dispersion of the sun’s light after rain or other water droplets in the atmosphere. The colours of the rainbow are generally said to be red, orange, yellow, green, blue, indigo and violet.
Each colour of rainbow makes a parabola. We know that for any quadratic polynomial ax2 + bx + c, a ≠ 0, the graph of the corresponding equation y = ax2 + bx + c has one of the two shapes either open upwards like ∪ or open downwards like ∩ depending on whether a > 0 or a < 0. These curves are called parabolas.
(a) A rainbow is represented by the quadratic polynomial x2 + (a + 1 )x + b whose zeroes are 2 and-3. Then
(i) a = -7, b = -1
(ii) a = 5, b =-1
(iii) a – 2, b = – 6
(iv) a – 0, b = – 6
(b) The polynomial x2 – 2x – (7p + 3) represents a rainbow. If -4 is zero of it, then the value of p is
(i) 1
(ii) 2
(iii) 3
(iv) 4
(c) The graph of a rainbow y=f(x) is shown below.
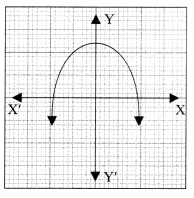
The number of zeroes of f(x) is
(i) 0
(ii) 1
(iii) 2
(iv) 3
(d) If graph of a rainbow does not intersect the x-axis but intersects y-axis in one point, then number of zeroes of the polynomial is equal to
(i) 0
(ii) 1
(iii) 0 OR 1
(iv) none of these
(e) The representation of a rainbow is a quadratic polynomial. The sum and the product of its zeroes are 3 and -2 respectively. The polynomial is 1
(i) k(x2 – 2x – 3), for some real k.
(ii) k(x2 – 5x – 9), for some real k.
(iii) k(x2 – 3x – 2), for some real k.
(iv) k(x2 – 8x + 2), for some real k.
Solution :
(a) x2 + (a + 1)x + b =(2)2 + (a + 1)2 + b = 0 and (-3)2 + (a + l)(-3) + b = 0
⇒ 4 + 2a + 2 + 6=0 and 9 — 3a — 3 + 6 = 0
⇒ 2a + b=-6 … (i)
and -3a + b=-6 …(ii)
Solving (i) and (ii), we get a = 0 and b = -6
So, option (iv) is correct answer.
(b) p(-4) = 0 ⇒ (-4)2 – 2(-4) – (7p + 3) = 0
⇒ 16 + 8 – 7p-3 = 0 ⇒ 21 – 7p = 0
⇒ p = 3
So, option (iii) is correct answer.
(c) ∵ Graph f(x) intersects x-axis at two different points.
∴ Number of zeroes of f(x) = 2.
So, option (iii) is correct answer.
(d) We know that the number of zeroes of a polynomial is equal to number of points of intersection of the graph of polynomial with x-axis.
Since the graph of rainbow does not intersect the x-axis, so it has no zeroes.
So, option (i) is correct answer.
(e) Let the required polynomial be f(x).
Then f(x) = k(x2 – 3x – 2) for some real k.
So, option (iii) is correct answer.
Question 20.
Case Study Based-4
| Cost of Living Index | 140-150 | 150-160 | 160-170 | 170-180 | 180-190 | 190-200 | Total |
| Number of weeks | 5 | 10 | 20 | 9 | 6 | 2 | 52 |
(a) The mid-value (class-mark) of 160-170 is ……..
(i) 140
(ii) 145
(iii) 155
(iv) 165
(b) The approximate mean weekly cost-of-living index is 1
(i) 166.4
(ii) 184.5
(iii) 190
(iv) 201.8
(c) The sum of lower and upper limits of modal class is
(i) 290
(ii) 310
(iii) 330
(iv) 350
(d) Mode is the value of the variable which has
(i) maximum frequency
(ii) minimum frequency
(iii) mean frequency
(iv) middle most frequency
(e) The median class of above data is
(i) 150-160
(ii) 160-170
(iii) 170-180
(iv) 190-200
Solution :
(a) Class-mark of 160-170 = \(160-170=\frac{160+170}{2}=\frac{330}{2}=165\)
So, option (iv) is correct answer.
| Cost of Living Index | No. of Weeks (fi) | Mid-point (xi) | fixi |
| 140-150 | 5 | 145 | 725 |
| 150-160 | 10 | 155 | 1550 |
| 160-170 | 20 | 165 | 3300 |
| 170-180 | 9 | 175 | 1575 |
| 180-190 | 6 | 185 | 1110 |
| 190-200 | 2 | 195 | 390 |
| Total | n = 52 | 8650 |
\(\text { Mean }=\frac{\sum f_{i} x_{i}}{\sum f_{i}}=\frac{8650}{52}=166.4(\text { approx. })\)
So, option (i) is correct answer.
(c) Maximum frequency is 20
∴ Modal class = 160-170
Lower limit of modal class = 160
Upper limit of modal class =170
Sum of lower and upper limits = 160 + 170 = 330
So, option (iii) is correct answer.
(d) (i) Maximum frequency
| Cost of Living Index | f | cf |
| 140-150 | 5 | 5 |
| 150-160 | 10 | 15 |
| 160-170 | 20 | 35 |
| 170-180 | 9 | 44 |
| 180-190 | 6 | 50 |
| 190-200 | 2 | 52 |
n= 52 \(\Rightarrow \frac{n}{2}=26\)
Median class is 160-170.
So, option (ii) is correct answer.
Part-B
Section-III
Question 21.
If two positive integers p and q are written as p = a2b2 and q = a3b; a, b are prime numbers, then verify: LCM (p, q) x HCF (p, q) =pq.
Answer:
LCM (p, q) =a3b3 and HCF (p, q) = a2b
LCM (p, q) x HCF (p, q) =a5b4 = (a2b3) (a3 b) = pq
Question 22.
Draw a line segment of length 6 cm. Using compass and ruler, find a point P on it which divides it in the ratio 3:4.
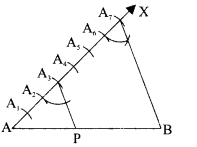
Solution :
Steps of construction:
1. Draw a line segment AB = 6 cm.
2. Draw an acute angle <BAX.
3. Along AX take 7 points, such that
AA1 — A1 A2 — A2 A3 — A3A4 — A4A5 – A5A6 — A6A7
4. Join BA7
5. Through A3 draw A3P A7B which meets AB at P.
6. AP: PB = 3 : 4 and P is the required point.
Question 23.
If 7 sin2 A + 3 cos2 A = 4, show that tan \(A=\frac{1}{\sqrt{3}}\)
OR
Prove that \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}=2 \sec A\)
Solution :

Question 24.
In the given figure, XY and XT’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and XT’ at B. Prove that ∠AOB = 90°.
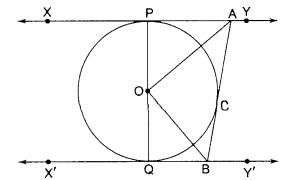
Solution :
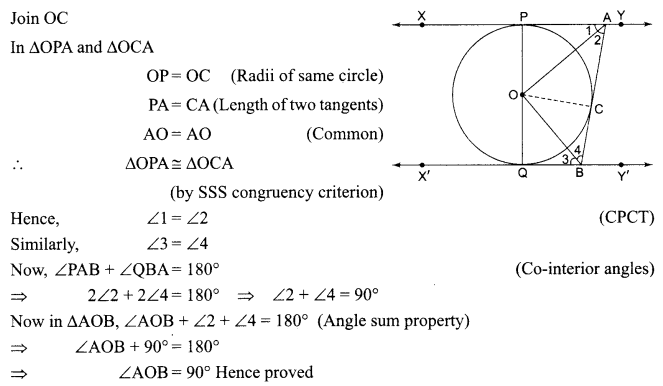
Question 25.
The coordinates of the points P and Q are respectively (4,—3) and (—1, 7). Find the x-coordinate (abscissa) of a point R on the line segment PQ such that \(\frac{P R}{P Q}=\frac{3}{5}\)
OR
Find the ratio in which the point (—3, k) divides the line segment joining the points (—5, —4) and (—2, 3). Also find the value of k.
Solution :

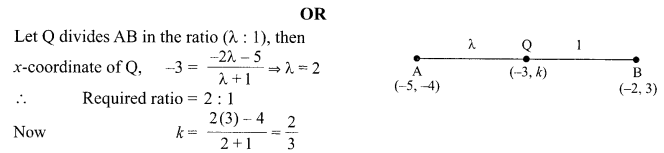
Question 26.
Find k, if the sum of the zeroes of the polynomial x2 – (k + 6) x + 2 (2k – 1) is half of their product.
Answer:
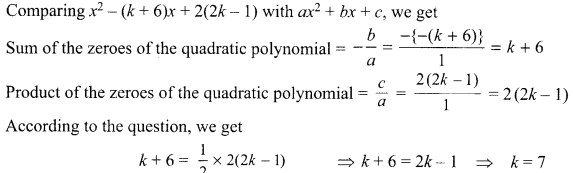
Section-IV
Question 27.
In a seminar, the number of participants in Hindi, English and Mathematics are 60, 84 and 108 respectively. Find the minimum number of rooms required if in each room the same number of participants are to be seated and all of them being of the same subject.
Solution :

Question 28.
In the given figure, ABPC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
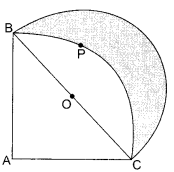
Solution :

Question 29.
Show that in a right triangle, the square of the hypotenuse is equal to the sum of the squares
of the other two sides.
OR
P is the mid-point of side BC of AABC, Q is the mid-point of AP, BQ when produced meets AC at L. Prove that AL = \(\frac{1}{3} \) AC.
Solution :
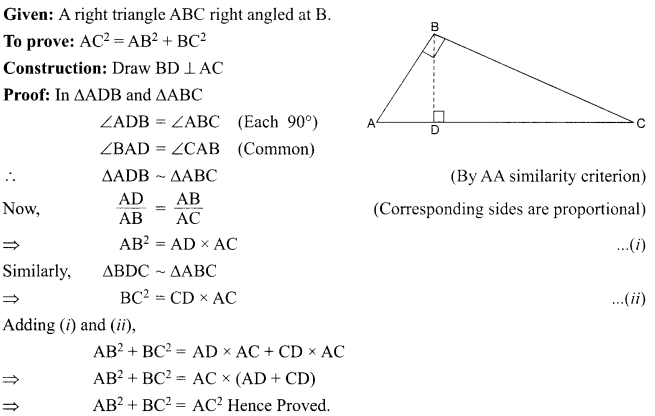
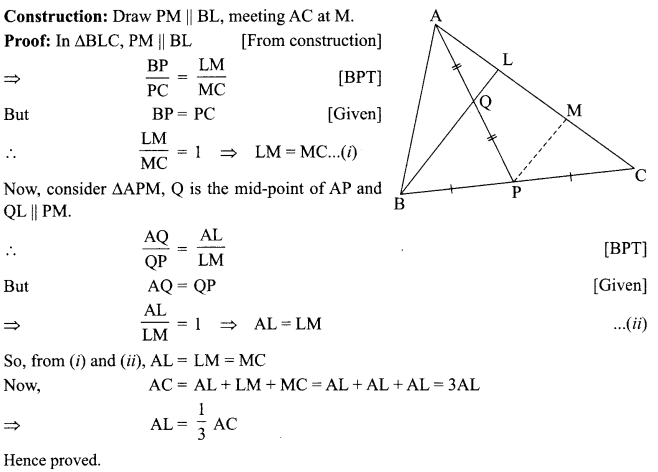
Question 30.
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency k.
| Daily pocket allowance (in ₹) |
11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| Number of children | 3 | 6 | 9 | 13 | k | 5 | 4 |
Solution :

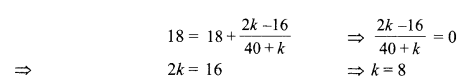
Question 31.
Using quadratic formula, solve the following equation for X:
abx2+(b2—ac)x—bc=O
OR
The difference of two natural numbers is 5 and the difference of their reciprocals is \(\frac{1}{10}\). Find the numbers.
Solution :

Let the two natural numbers be x and y such that x >y
According to the question,
Difference of numbers,
x – y = 5 ⇒ x = 5 +y ……………(1)
Difference of their reciprocals,
\(\frac{1}{y}-\frac{1}{x}=\frac{1}{10}\)
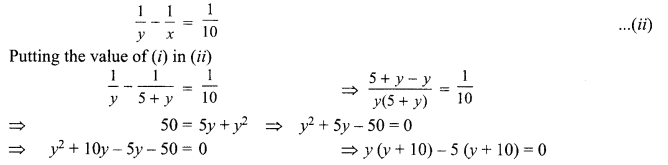
= (y – 5)(y + 10) = 0 ∴ y = 5 or y = – 10
y is a natural number. ∴ y = 5
Putting the value of)’ in (i), we get
x= 5+5=10
Thus, the required numbers are 10 and 5.
Question 32.
Find the angle of depression from the top of 12m high tower of an object lying at a point 12 m away from the base of the tower.
Solution :
Let AB be the tower of 12 m height and B its base. Let C be a point A 12 m away from base B of tower AB where an object situated.
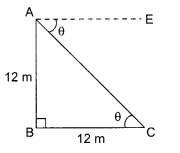
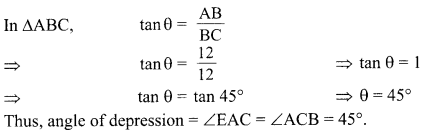
Question 33.
If the median of the distribution given below is 28.5, find the values of x and y.
| Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | Total |
| Frequency | 5 | X | 20 | 15 | y | 5 | 60 |
Solution :
Here, median = 28.5, n = 60
| Class interval | Frequency (f) | Cumulative frequency (cf) |
| 0-10 | 5 | 5 |
| 10-20 | X | 5 + x |
| 20-30 | 20 | 25 + x |
| 30-10 | 15 | 40+ x |
| 40-50 | y | 40 + x + y |
| 50-60 | 5 | 45+x + y |
| Total | ∑ fi = 60 |

Section – V
Question 34.
The angles of depression of the top and bottom of a building 50 metres high as observed from the top of a tower are 30° and 60°, respectively. Find the height of the tower and also the horizontal distance between the building and the tower.
OR
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Solution :
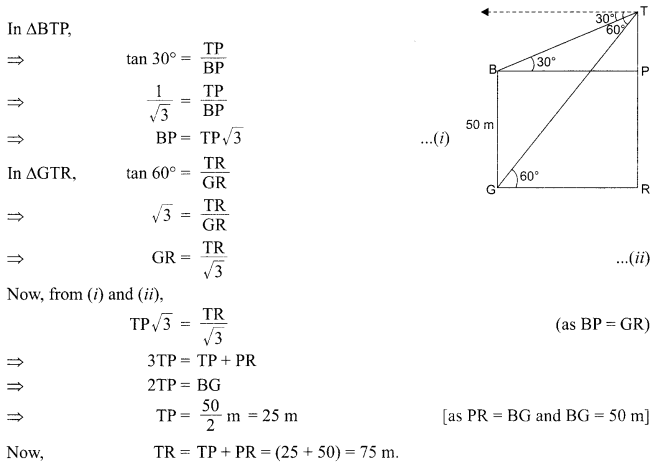


Thus, height of the other tower = 10 m and the distance between two towers = BD = 10√3 m.
Question 35.
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block.
Solution :

Question 36.
A person can row 8 km upstream and 24 km downstream in 4 hours. He can row 12 km downstream and 12 km upstream in 4 hours. Find the speed of the person in still water and also the speed of the current. 5
Solution :
Let the person’s speed of rowing in still water be, x km/h and speed of the current y km/h.
∴ Speed of boat in downstream = (x + y) km/h
and speed of boat in upstream = (x -y) km/h
Since \(\text { Time }=\frac{\text { Distance }}{\text { Speed }}\)