Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 3 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Set 3 with Solutions
Time: 3 Hours
Maximum Marks: 80
General Instructions:
1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.
Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Section-I
Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
Question 1.
If one of the zeroes of the quadratic polynomial x1 + 3x + k is 2, then find the value of k
Solution :
Since 2 is a zero of p(x) = x2 + 3x + k, then p(x) =0
⇒(2)2 + 3 x 2 + k = 0
⇒ 4 + 6 + k = 0
⇒ k = -10
Question 2.
Find the total number of factors of a prime number.
OR
Find the HCF and the LCM of 12, 21, 15.
Solution :
We know that prime number is a number which has exactly two factors, i.e., 1 and the number itself. So, the total number of factors of a prime number is 2.
OR
12 = 2 x 2 x 3 = 22 x 31
15 = 3 x 5 = 31 x 51 21 = 3 x 7 = 31 x 71 HCF(12, 15,21)= 3
LCM(12, 15, 21) = 22 x 31 x 51 x 71 = 4 x 3 x 5 x 7 = 420
Question 3.
Find the value of k for which the system of equations x + y – 4 = 0 and 2x + ky = 3, has no solution.
Solution :
For the equations, x + y -4 = 0 and 2x + ky = 3
⇒ 2x + ky – 3 = 0
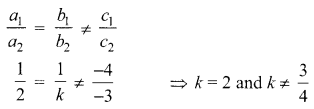
Question 4.
Find the value of x for which 2x, (x + 10) and (3x + 2) are the three consecutive terms of an AP.
OR
The first term of an AP is p and the common difference is q. Find its 10th term.
Solution :
2x (x + 10) and (3x + 2) are three consecutive terms of an AP.
Then, (x+10)-2x= (3x + 2)-(x+10)
⇒ x + 10 – 2x = 3x + 2 – x – 10
⇒ -x + 10 = 2x- 8
⇒ 3x = 18
⇒ x = 6
an = a + (n – 1 )d ⇒ am =p + (10 – 1 )q =p + 9q
a10 = p + 9q
Question 5.
In figure, ΔABC is circumscribing a circle. Find the length of BC.
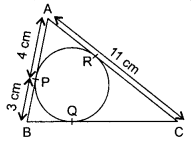
Solution :
Line segments AB, BC and AC are tangents of the circle.
AP = AR = 4 cm …(i)
[Tangents drawn from the same point to a circle are equal]
Similarly, BP = BQ = 3 cm ……………… (ii)
and CQ = CR ………….. (iii)
Since, AC =11 cm ⇒ AR + CR = 11 cm
⇒ 4 cm + CR = 11 cm [from (i)]
⇒ CR = 7 cm ……………… (iv)
BC = BQ + CQ = 3 cm + 7 cm [From (ii),(iii) and (iv)]
= 10 cm
Question 6.
If in the given figure, DE || BC, then find EC.
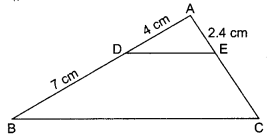
Solution :
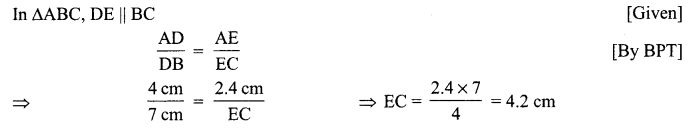
Question 7.
Find the value of \(\left(\sin ^{2} \theta+\frac{1}{1+\tan ^{2} \theta}\right)\)
Solution :
\(\sin ^{2} \theta+\frac{1}{1+\tan ^{2} \theta}=\sin ^{2} \theta+\frac{1}{\sec ^{2} \theta}=\sin ^{2} \theta+\cos ^{2} \theta=1\)
Question 8.
Find the value of (1 + tan2 θ) (1 – sin θ) (1 + sin θ).
Solution :
(1 + tan2 θ)(1 – sin θ)(1 + sin θ) = (1 + tan2 θ)(1 – sin2 θ)
\(=\sec ^{2} \theta \cos ^{2} \theta=\frac{1}{\cos ^{2} \theta} \times \cos ^{2} \theta=1\)
Question 9.
Two cones have their heights in the ratio 1 : 3 and radii in the ratio 3:1. What is the ratio of their volumes? 1
Solution :
Let h1 and h2 be the heights of two cones and r1 and r2 by the radii
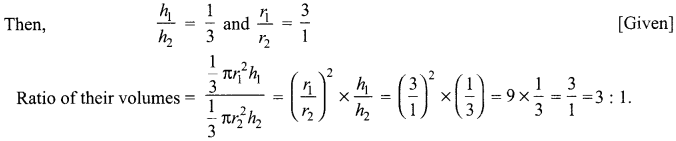
Question 10.
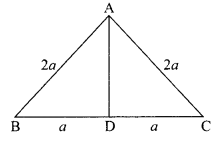
If ABC is an equilateral triangle of side 2a, then find the length of one of its altitudes.
OR
In the given figure, MN || QR. If PM = x cm, MQ = 10 cm, PN = (x – 2) cm, NR = 6 cm, then find the
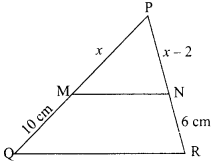
Solution :
In ∠ADB and ∠ADC,
AB = AC [Sides of equilateral triangle ABC]
AD = AD [Common]
∠ADB = ∠ADC [90°, AD ⊥ BC]
ΔADB ≅ ΔADC
ABC is an equilateral triangle such that each side is 2a and AD ⊥ BC.

Question 11.
Base of an isosceles triangle is \(\frac{2}{3}\) times its congruent sides. Perimeter of the triangle is 32 cm.
Formulate this problem as a pair of equations.
Solution :
Let the congruent side of isosceles triangle be x cm and its base be y cm.
Then \(y=\frac{2}{3} x\)
2x – 3y = 0 ……………. (i)
Also, x + x + y=32 ⇒ 2x + y = 32 ………….. (ii)
Question 12.
Check whether x(x + 2) – 3 = (x+ 4)x is a quadratic equation.
Solution :
Since x(x + 2) – 3 = x(x + 4)
⇒ x2 + 2x – 3 = x2 + 4x
⇒ 2x + 3 = 0
This is linear equation not a quadratic equation.
Question 13.
Is x = -2 a solution of 3x2 + 13x + 14 = 0?
OR
State whether the equation (x + 1) (x – 2) + x = 0 has two distinct real roots or not. Justify your answer.
Solution :
Putting the value of x in the quadratic equation,
LHS = 3x2 + 13x + 14 = 3 (-2)2 + 13 (-2) + 14
= 12 – 26 + 14 = 0 = RHS
Hence, x = -2 is a solution.
OR
We have (x + 1) (x – 2) + x = 0
⇒ x2-x-2 + x= 0 ⇒ x2-2 = 0
D = b2 – 4ac = 0 – 4(1) (-2) = 8 > 0
∴ Given equation has two distinct real roots.
Question 14.
Two concentric circles of radii a and b (a> b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
OR
In the given figure, CP and CQ are tangents from an external point C to a circle with centre O. AB is another tangent which touches the circle at R. If CP = 11 cm and BR = 4 cm, find the length of BC.
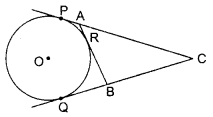
Solution :
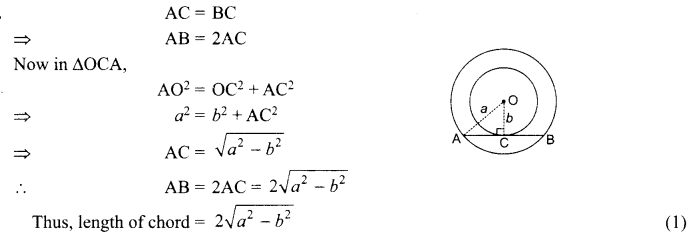
OR
In the given figure, CP = CQ [tangents drawn from an external point are equal]
So, CP = CQ = 11 cm
Also, BR = BQ [tangents drawn from an external point are equal]
So, BR = BQ = 4 cm
∴ Now, BC = CQ – BQ
= (11 -4) cm = 7 cm
Question 15.
Draw a line segment of length 6 cm. Using compasses and ruler, find a point P on it which divides it in the ratio 3:4.
Solution :
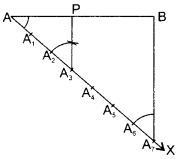
Steps of construction:
1. Draw a line segment AB = 6
2. Draw any ray AX making an acute angle XAB with AB.
3. Along AX mark 7 (3 + 4) points A1 A2, A3, A4,……………, A7 at equal distances such that
AA1 = A1A2 = A6A7
4. Join A7B
5. From A3, draw A3P parallel to A7B (by making an angle equal to ∠AA7B at A3) to meet AB at point P.
Then AP : PB = 3 : 4.
Question 16.
The radius of a circle is 5 cm. Find the circumference of the circle whose area is 49 times the area of given circle.
Solution :
The area of the given circle = πr2 = π(5)2 = 25π sq. cm
Area of the other circle = 49 × 25π
Let the radius of this circle be R Then
Then πR2 = 49 x 25 x π ⇒ R2 = (7)2 x (5)2
R = 7 x 5 = 35 cm
The required circumference = 2πR = 2 x \(\frac{22}{7}\) x 35 = 220 cm
Section-II
Case Study based questions are compulsory. Attempt any four sub-parts of each question. Each sub-part carries 1 mark.
Case Study Based-1
Question 17.
Treasure Island Shikha and Sanjana are playing a board game of
Treasure Island.
Shikha and Sanjana are playing a board game of Treasure Island.
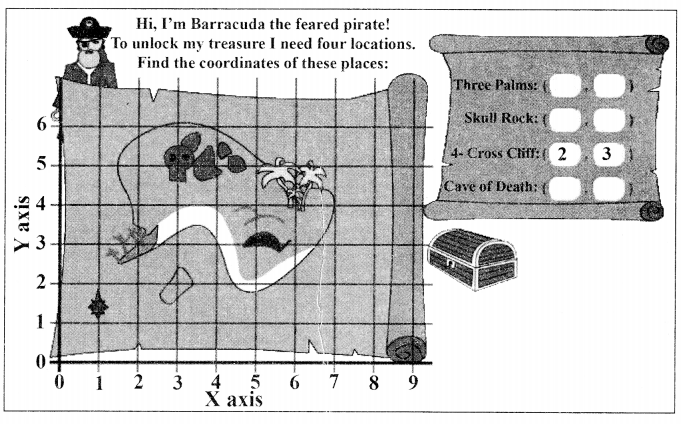
Refer to Skull Rock and Cave of Death
(a) The mid-point of the segment joining A(3, 5) and C(5, 3) is……..
(i) (2,3)
(ii) (3,5)
(iii) (4,3)
Refer to Three Palms
(b) The distance of point D(6, 4) from origin is
(i) \(5 \sqrt{7}\)units
(ii) \(7 \sqrt{5}\) units
(iii) \(4 \sqrt{10}\) units
(iv) \(2 \sqrt{23}\) units
Refer to 4-Cross Cliffs and Three Palms
(c) The distance between the points B(2,3)and D(6, 4) is
(i) \(\sqrt{13} \text { units }\)units
(ii) 4 units
(iii) \(5 \sqrt{3}\)units
(iv) \(\sqrt{17}\)units
(d) The coordinate of the point which divides the join of B(2,3) and D(6,4) in the ratio 2 : 3 is
(i) \(\left(\frac{13}{4}, \frac{19}{4}\right)\)
(ii) \(\left(\frac{18}{5}, \frac{17}{5}\right)\)
(iii) \(\left(\frac{11}{8}, \frac{13}{8}\right)\)
(iv) \(\left(\frac{19}{3}, \frac{16}{3}\right)\)
(e) If \(P\left(\frac{x}{3}, 4\right)\) is the mid-point of the line segment joining the points C(5,3) and
A(3, 5), then
(i) 8
(ii) 10
(iii) 12
(iv) 16
Solution :


Case Study Based-2
Question 18.
What are you Smoking?
Given below is Air Quality Index of different localities of Delhi on 27th December 2019 by Times of India Newspaper on 28th. December 2019
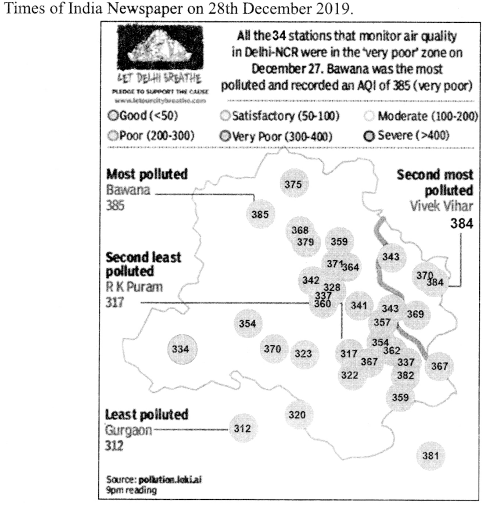
The data recorded from above AQI (Air Quality Index) is given below:
| AQI | 310-320 | 320-330 | 330-340 | 340-350 | 350-360 | 360-370 | 370-380 | 380-390 |
| Frequencies | 2 | 4 | 3 | 4 | 5 | 7 | 5 | 4 |
(a) The sum of the lower limits of the median class and modal class is ……………
(i) 650
(ii) 660
(iii) 750
(iv) 710
(b) The modal class is …………
(i) 310-320
(ii) 330-340
(iii) 360-370
(iv) 380-390
(c) The upper limit of the median class is ………
(i) 330
(ii) 350
(iii) 360
(iv) 390
(d) The difference of the upper limit of the median class and the lower limit of the modal class is ……..
(i) 0
(ii) 1
(iii) 2
(iv) 3
(e) The mean AQI is ……..
(i) 335.8
(ii) 354.7
(iii) 360.4
(iv) 395.9
Solution :
| Class | Frequency | Cumulative Frequency |
| 310-320 | 2 | 2 |
| 320-330 | 4 | 6 |
| 330-340 | 3 | 9 |
| 340-350 | 4 | 13 |
| 350-360 | 5 | 18 ← Median Class |
| 360-370 | 7 | 25 ← Model Class |
| 370-380 | 5 | 30 |
| 380-390 | 4 | 34 |
| n= 34 |
We have \(n=34, \frac{n}{2}=\frac{34}{2}=17\)
∴ The sum of the lower limits of the median class and modal class = 350 + 360 = 710 So, option
(iv) is the correct answer.
(b) Here, the maximum frequency is 7 and the corresponding class is 360-370.
So, modal class is 360-370. So, option (iii) is the correct answer.
(c) The median class is 350-360 which has upper limit 360. So, option (iii) is the correct answer.
(d) The difference between upper limit of the median class and the lower limit of the modal class = 360 – 360 = 0. So, option (i) is the correct answer.
(e)
| Class | Frequency (fi) | Class Mark (xi) |
fi xi |
| 310-320 | 2 | 315 | 630 |
| 320-330 | 4 | 325 | 1300 |
| 330-340 | 3 | 335 | 1005 |
| 340-350 | 4 | 345 | 1380 |
| 350-360 | 5 | 355 | 1775 |
| 360-370 | 7 | 365 | 2555 |
| 370-380 | 5 | 375 | 1875 |
| 380-390 | 4 | 385 | 1540 |
| ∑fi = 34 | ∑fi xi = 12060 |
\(\text { Mean }=\frac{\sum f_{i} x_{i}}{\sum f_{i}}=\frac{12060}{34}=354.7(\text { approx. })\)
So, option (ii) is the correct answer.
Case Study Based-3
Question 19.
Skipping Rope
Skipping rope is a good exercise. It bums calories, makes bones strong and improves heart health.
During skipping, when rope goes up and down it makes the shape of parabolas (graphs of quadratic polynomials). Observe the following skipping pictures.
Refer Picture 1
(a) The graph of polynomial p(x) represented by Picture 1 is shown below. The number of zeroes of the polynomial is
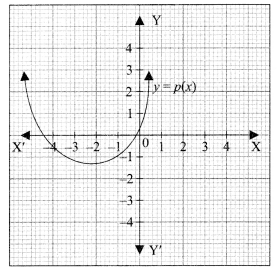
(i) 0
(ii) 1
(iii) 2
(iv) 4
Refer Picture 2
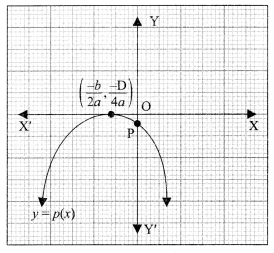
(b) The graph of polynomial p(x) represented by Picture 2 is shown below. Which of the following has negative (-) sign?
(i) a
(ii) b
(iii) c
(iv) All of there
(c) If \(\frac{1}{4}\) and 1 are the sum and product of zeroes of a polynomial whose graph is represented by Picture (3), the quadratic polynomial is
(i) \(k\left(x^{2}-\frac{1}{4} x-1\right)\)
(ii) \(k\left(\frac{1}{4} x^{2}-x-1\right)\)
(iii) \(k\left(x^{2}+\frac{1}{4} x+1\right)\)
(iv) \(k\left(\frac{1}{4} x^{2}+x+1\right)\)
(d) Let the Picture (1) represent the quadratic polynomial f(x) = x2 – 8x + k whose sum of the
squares of zeroes is 40, The value of k is
(i) 8
(ii) 10
(iii) 12
(iv) 20
(e) Let the Picture (3) represent the quadratic polynomial f(x) = x2 + 7x + 10. Then its zeroes are
(i) -1, -5
(ii) -2, -5
(iii) 1, 5
(iv) 2, 5
Solution :
(a) Since the graph y p(x) cuts the x-axis at two different points, so the polynomial has two zeroes. So, option (iii) is the correct answer.
(b) The parabola)’ = ax2 + bx + c open downwards. Therefore, a <O. The vertex \(\left(\frac{-b}{2 a}, \frac{-\mathrm{D}}{4 a}\right)\) of the parabola is on OX1.
\( \quad \frac{-b}{2 a}<0 \quad \Rightarrow b<0\)
Parabola y =p(x) cuts y-axis at P(O, c) which lies on OY’. Therefore e <O.
Hence, O, b <O and c< O.
So, option (iv) is the correct answer.
(c) We have sum \(\frac{1}{4}\) and product
\(f(x)=k\left(x^{2}-\frac{1}{4} x-1\right)\)
So, option (iii) is the correct answer.
(d) 
(e) We have
x2 + 7x + 10 =x2 + 5x + 2x + 10 = x(x + 5) + 2(x + 5) = (x + 2)(x + 5)
Now, when x + 2 = 0 or x + 5 = 0, i.e., whenx = -2 andx = -5
Therefore, the zeroes of x2 + lx + 10 are -2 and -5
Question 20.
Fair Play
Garima has two children, Tapan and Maya. Every Sunday is a game night in the family. Tonight Garima has planned for a game with three cubes, one purple and two yellow. She placed the three cubes in a bag and called for her children.
Garima: Do you want to play a game of probability?
Maya: What is probability?
Garima: Let me ask you something before I answer you. Can you predict what is in this bag?
Tapan: I cannot guess that!
Maya: I am 100% sure it is a toy!
Garima: I am glad you think that Maya. Just now you used the concept of probability.
Whether an event can happen or not, can’t be predicted with total certainty. But we can always predict how- likely or unlikely it is for an event to happen.
And for predicting that, we use a concept called probability.
\(\text { Probability (an event to happen) }=\frac{\text { Number of ways event can happen }}{\text { Total number of ways all events can happen }}\)
Placing the bag of cubes in the centre, Garima explained the rules of the game to the children. Garima: Without looking, the first player will pick out a cube from the bag and then the second player will also pick out one cube without looking. If the two cubes picked out were the same colour, then the first person will win the game. If the boxes picked out are of two differently coloured cubes, then the second player will be the winner.
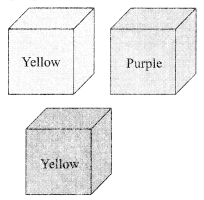
(a) In the first round, Maya pulled out a cube, which was yellow. What is the probability that Tapan will win the game?
(i) \(\frac{1}{2}\)
(ii) \(\frac{1}{3}\)
(iii) \(\frac{2}{3}\)
(iv) 0
(b) in the second round, Tapan started by picking out a purple cube. What is the probability for Tapan to win the round?
(i) 1
(ii) \(\frac{1}{3}\)
(iii) 0
(iv) \(\frac{2}{3}\)
(c) In the third round, Maya pulled out a cube. The probability that the pulled out cube is not of yellow colour is
(i) 1
(ii) \(\frac{1}{2}\)
(iii) \(\frac{1}{3}\)
(iv) \(\frac{2}{3}\)
(d) In the fourth round, Tapan pulled out a cube. The probability that the pulled out cube is either purple or yellow is
(i) 1
(ii) \(\frac{1}{2}\)
(iii) \(\frac{1}{3}\)
(iv) \(\frac{2}{3}\)
(e) In the last round, Maya pulled out a cube. The probability that the pulled out cube is of green colour is
(i) 1
(ii) \(\frac{1}{2}\)
(iii) \(\frac{1}{3}\)
(iv) 0
Solution :
(a) After taking out one yellow cube, the bag is left with 1 yellow cube whose probability of pulling out \(\frac{1}{2}\) So, option (i) is the correct answer.
(b) After taking out one purple cube, the bag has no purple cube. So, the probability for Tapan to win the round is
\(\frac{0}{3}\) = 0
So, option (iii) is the correct answer.
(c) The number of yellow cube is 1. So, the probability of pulling out a cube not of yellow colour is \(\frac{1}{3}\)
So, option (iii) is the correct answer.
(d) The number of purple and yellow cubes =1 + 2 = 3.
∴ The required probability =\(\frac{3}{3}\) = 1
So, option (i) is the correct answer.
(e) The number of green cube = 0
.’. The required probability = \(\frac{0}{3}\) = 0
So, option (iv) is the correct answer.
Part-B
Section-III
All questions are compulsory. In case of internal choices, attempt any one.
Question 21.
Write a rational number between \(\sqrt{2} \text { and } \sqrt{3}\)
Solution :
We have √2 =1.4142135…. and √3 = 1.7320508…
Since every terminating decimal or repeating decimal represents a rational number.
So, 1.666666… is a rational number between \(\sqrt{2} \text { and } \sqrt{3}\)
Also 1.5, 1.6, 1.7 are rational numbers between \(\sqrt{2} \text { and } \sqrt{3}\)
Question 22.
Find the ratio in which the point (-3, p) divides the line segment joining the points (-5,-4) and (-2,3).
Hence find the value of p.
OR
If the point C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 : 4, find the coordinates of B.
Solution :
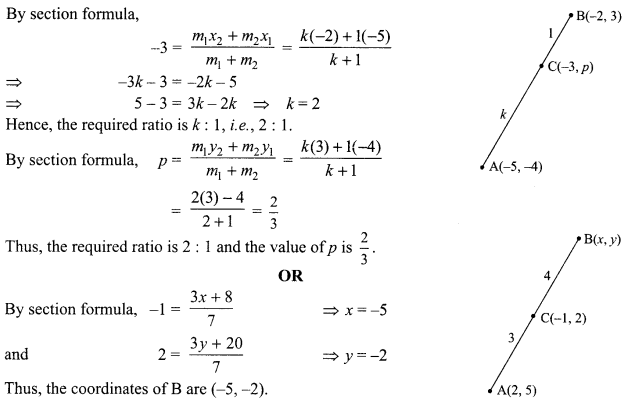
Question 23.
Find a quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial f(x)=ax2+bx+c,a≠0,c≠0.
Solution :
Let the zeroes of the polynornial f(x) = ax2 + bx + c be α and β.
Then \(\alpha+\beta=\frac{-b}{a} \text { and } \alpha \beta=\frac{c}{a}\)
Now, the zeroes of the required polynomial are reciprocals of a and p.
∴ The required quadratic polynomial is given by
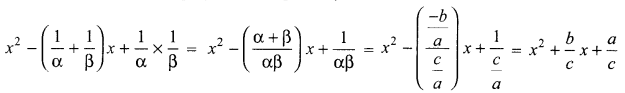
Question 24.
Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.
Solution :
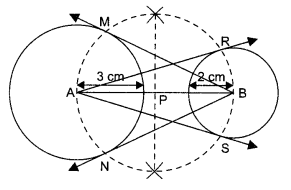
Steps of construction:
1. Draw a line segment AB of length 7 cm.
2. With A as centre, draw a circle of radius 3 cm.
3. With B as centre, draw a circle of radius 2 cm.
4. Draw the perpendicular bisector of AB. Let P be the mid-point of segment AB.
5. With P as centre and radius PA draw a circle which intersects the circle with centre A at M and the circle with centre B at R and S.
6. Join BM and BN. Also join AR and AS. Then, BM, BN, AR and AS are required tangents.
Question 25.
The rod AC of a TV disc antenna is fixed at right angles to the wall AB and a rod CD is supporting the disc as shown in figure. If AC = 1.5 m and CD = 3 m, then find
(a) tan θ
(b) sec θ + cosec θ
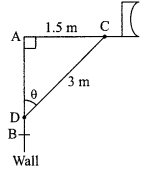
If sin θ + cosθ = √3, then prove that tan θ + cot θ = 1.
Solution :

Question 26.
In the given figure, two tangents TP and TQ are drawn to a circle with centre O from an external point T
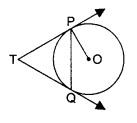
Prove that: ∠PTQ = ∠OPQ.
Solution :
We know that, tangents drawn from same external point are equal.
Section-IV
Question 27.
Find HCF and LCM of 404 and 96 and verify that HCF x LCM = product of the two given numbers.
Solution :
404 = 2 x 2 x 101 =22 x 101
96 = 2 x 2 x 2 x 2 x 2 x 3 = 25 x3
∴ HCF of 404 and 96 = 22 = 4
LCM of 404 and 96 = 101 x 25 x 3 = 9696 HCF x LCM
= 4 x 9696 = 38784
Also 404 x 96 = 38784
Hence HCF x LCM = Product of 404 and 96.
Question 28.
If the roots of the equation (a – b)x2 + (b – c )x + (c – a) = 0 are equal, prove that 2a = b + c.
OR
The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
Solution :
For real and equal roots, D = 0 ⇒ (b – c)2 – 4(a – b)(c -a) = 0
⇒ b2 + c2 – 2be – 4ac + 46c + 4a2 – 4ab = 0
⇒ 4a2 + b2 + c2 – 4ab + 2 be – 4ac = 0
⇒ (-2a)2 + (b)1 + (c)2 + 2(-2 a)b + 2 (b)(c) + 2c(-2a) = 0
⇒ ( – 2a + b + c)2 = 0 ⇒ – 2a + b + c = 0
⇒ 2 a = b + c
OR
Let the two consecutive odd numbers be x and x +2
x2 + (x + 2)2 = 394 ⇒ x2 + x2 + 4 + 4x = 394
⇒ 2x2 + 4x + 4 = 394 ⇒ 2x2 + 4x – 390 = 0
⇒ x2 + 2x – 195 = 0 ⇒ x2 + 15x – 13x – 195 = 0
⇒ x (x + 15) – 13 (x + 15) = 0 ⇒ (x- 13) (x+ 15) = 0
x – 13 = 0 ⇒ or x + 15 = 0
⇒ x= 13 ⇒ or x = – 15 (neglected)
When the first number x = 13, then the second number x + 2 = 13 + 2= 15.
Question 29.
ABCD is a square of side 4 cm. At each comer of the square, a A quarter circle of radius 1 cm, and at the centre, a circle of radius 1 cm, are drawn, as shown in the given figure. Find the area of the shaded region.
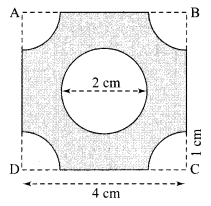
Solution :
Area of the shaded portion
= Area of given square ABCD
– 4 x area of each quarter circle
– area of the circle at the centre.
Question 30.
In the given figure, \(\angle \mathrm{D}=\angle \mathrm{E} \text { and } \frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) prove that ΔBAC is an isosceles triangle.
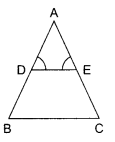
OR
Prove that the sum of squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
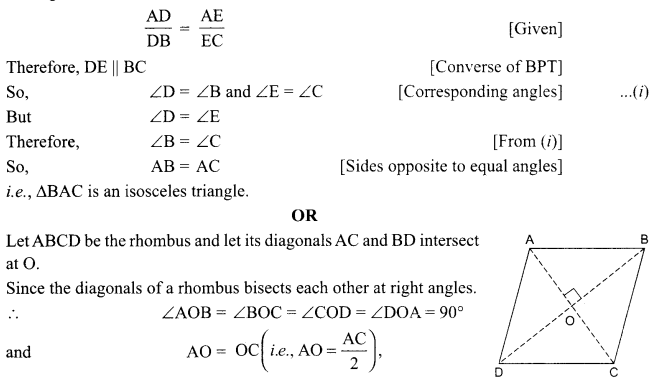
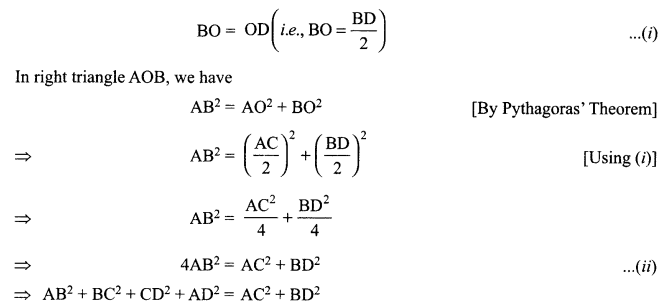
[ ∴ AB = BC = CD = AD, sides of a rhombus]
Hence, the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Question 31.
In the given figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
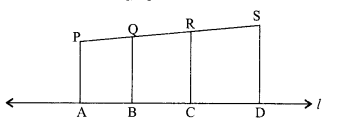
Solution :
If three or more line segments are perpendiculars to one line, then they are parallel to each other.

Question 32.
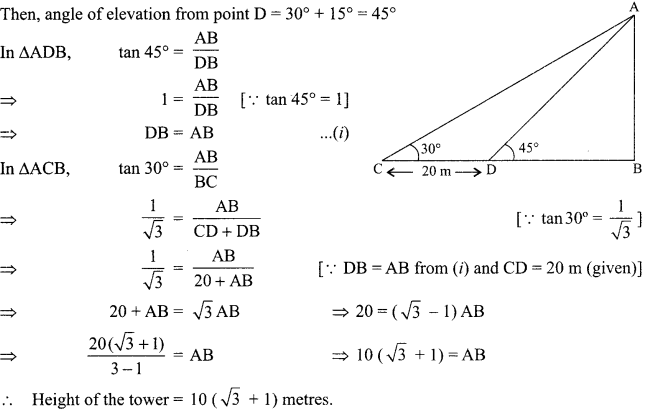
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
Solution:
Let AB be the tower and angle of elevation from point C = 30°
Question 33.
The median of the following data is 525. Find the values ofx andy, if total frequency is 100.
| Class | 0-100 | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 | 700-800 | 800-900 | 900-1000 |
| Frequency | 2 | 5 | X | 12 | 17 | 20 | y | 9 | 7 | 4 |
Solution:
| Class | Frequency | cf |
| 0-100 | 2 | 2 |
| 100-200 | 5 | 1 |
| 200-300 | X | 7 + x |
| 300-400 | 12 | 19+x |
| 400-500 | 17 | 36+x |
| 500-600 | 20 | 56 +x |
| 600-700 | y | 56 + x +y |
| 700-800 | 9 | 65 + x + y |
| 800-900 | 7 | 72 +x+y |
| 900-1000 | 4 | 16+ x + y |
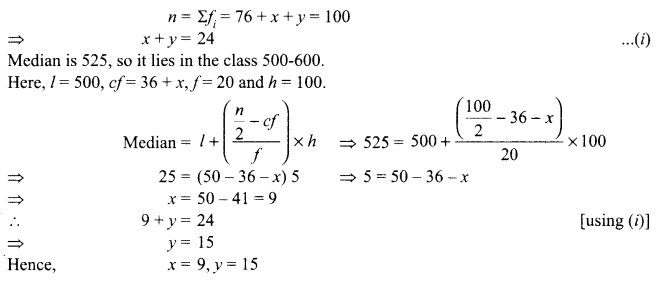
Section – V
Question 34.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 6 m. At a point on the plane, the angle of elevation of the bottom and top of the flagstaff are 30° and 45° respectively. Find the height of the tower. (Take 73 = 1.73)
OR
A vertical tower stands on a horizontal plane and is surmounted by a flag-staff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flag-staff are 60° and 30° respectively. Find the height of the tower and the distance of the point from base of the tower.
Solution :
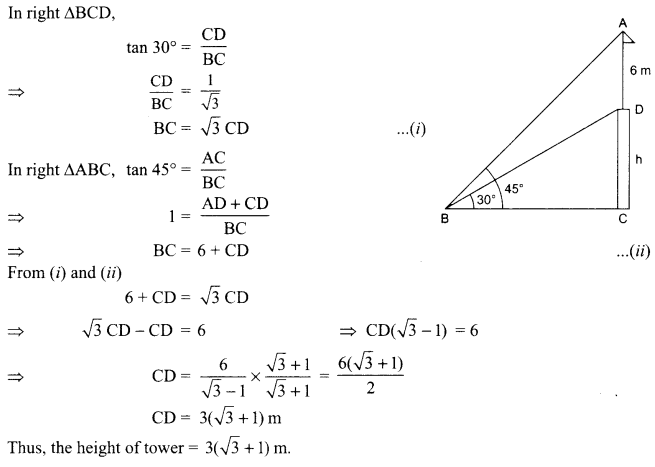
Or
Let height of tower (TR) be x m, distance (RP) of a point from the base of tower be y m, height of the flag-staff (QT) be 5 m. Then in the ΔTRP,

Question 35.
A toy is in the form of a right circular cylinder with a hemisphere on one end and a cone on the other. The height and radius of the cylindrical part are 13 cm and 5 cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Calculate the surface area of the toy if the height of the conical part is 12 cm.
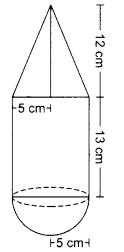
Solution :
Let r be the radius and h the height of the cylindrical part of the toy.
Then, r = 5 cm and h = 13 cm.
Let, r1 be the radius of the conical part, h1 its height and 1 its slant height.
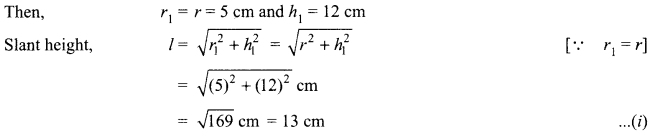

Question 36.
A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Solution :
Let the speed of the boat in still water be x km/h and the speed of the stream be y km/h.
∴ Speed of the boat going upstream = (x-y) km/h and
speed of the boat going downstream = (x + y) km/h

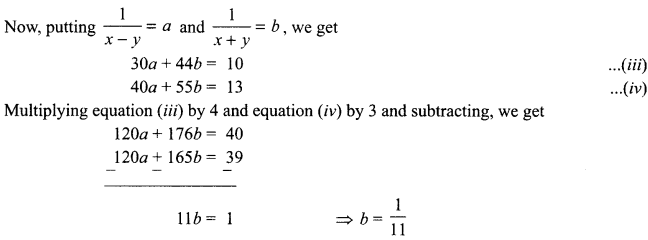
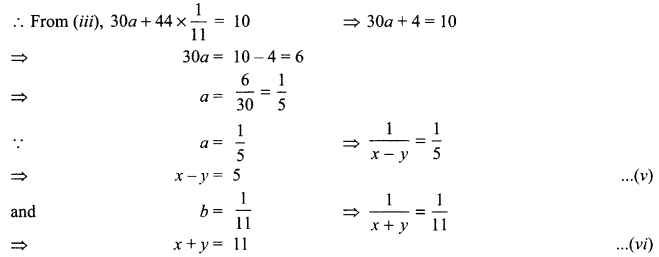
On solving (v) and (vi), we get x = 8, y = 3
Hence, speed of the boat in still water = 8 km/h and speed of the stream = 3 km/h.