CBSE Sample Papers for Class 10 Maths Standard Set 4 for Practice

Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Set 4 for Practice

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.

Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.

Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.

Part – A
Section-I

Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.

Question 1.
Find the distance between the lines 2x + 4 = 0 and x – 5 = 0.
OR
Find the distance of P (3, -2) from the y-axis.
Solution:
7 units OR 3 units

Question 2.
Find the value of k for which the given system has unique solution. 2x + 3y – 5 = 0, kx – 6y – 8 = 0
Solution:
k ≠ – 4

Question 3.
If cosec \(\theta=\frac{5}{3} \), then find the value of cos θ + tan θ.
Solution:
\(\frac{31}{20}\)

Question 4.
The given figure is a sector of circle of radius 10.5 cm. Find the perimeter of the sector.  [Take π = \(\frac{22}{7}\) ]

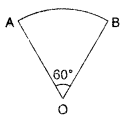
Solution:
32 cm

Question 5.
If in an equilateral triangle, the length of the median is √3 cm, then find the length of the side of equilateral triangle.
OR
In an equilateral triangle of side 3 √3 cm, find the length of the altitude.
Solution:
2 cm OR 4.5 cm

Question 6.
Find the nature of roots of ax² + bx + c = 0, a > 0, b = 0, c > 0.
Solution:
no real roots

Question 7.
Is x = – 3 a solution of x² + 6x + 9 = 0?
OR
What will be the nature of roots of quadratic equation 2x² + 4x -7 = 0?
Solution:
Yes OR Real and unequal

Question 8.
In the given figure, ABC is circumscribing a circle. Find the length of BC.

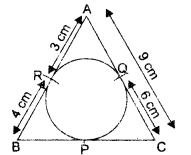
Solution:
10cm

Question 9.
In the given figure, O is the centre of the circle, PA and PB are tangents to the circle. Find the measure of ∠AQB.

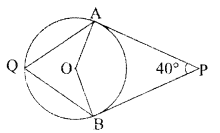
OR
In the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

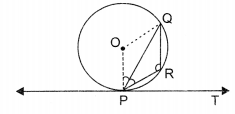
Solution:
70° OR 120°

Question 10.
ΔABC is isosceles in which ∠C = 90°. If AC = 6 cm, then find AB².
Solution:
72 cm²

Question 11.
To divide line segment AB in the ratio m : n, a ray AX is drawn so that ∠B AX is an acute angle and then points are marked on ray AX at equal distance. Find the minimum number of these points.
Solution:
m + n

Question 12.
If a, p are the zeroes of the polynomial 2y² + 1y + 5, write the value of a + p 4- a,p.
Solution:
-1

Question 13.
Form a quadratic polynomial, the sum and product of whose zeroes are (-3) and 2 respectively.
Solution:
x² + 3x + 2

Question 14.
For which values of k will the pair of equations kx + 3y = k – 3 and 12x + ky = k have no solution?
Solution:
k = – 6

Question 15.
Find the number of spherical lead shots each 4.2 cm in diameter can be obtained from a rectangular solid lead with dimensions 66 cm, 42 cm and 21 cm.
Solution:
1500

Question 16.
Find the probability of
(a) an impossible event.
(b) a sure event.
OR
Find the probability that a number selected at random from the number 1, 2, 3, …, 35 is a multiple of 7.
Solution:
(a) 0
(b) 1
OR
\(\frac{1}{7}\)

Section-ll

Case Study based questions are compulsory. Attempt any four sub-parts of each question. Each sub-part carries 1 mark.

Case Study Based-1

Question 17.
Traffic Lights

Traffic Lights (or traffic signals) are lights used to control movement of traffics. They are placed on roads at intersections and crossings. The different colours of light tell drivers what to do. The traffic lights at different road crossings change after every 48 sec, 72 sec and 108 sec respectively.

(a) 108 can be expressed as a product of its primes as ……….
(i) 2³ x 3²
(ii) 2³ x 3³
(iii) 2² x 3²
(iv) 2² x 3³
Solution:
(iv) 2² x 3³

(b) The HCF of 48, 72, 108 is ………..
(i) 18
(ii) 16
(iii) 12
(iv) 10
Solution:
(iii) 12

(c) The LCM of 48, 72, 108 is ……….
(i) 520
(ii) 432
(iii) 396
(iv) 420
Solution:
(ii) 432

(d) If all the traffic lights change simultaneously at 8:20:00 hrs, they will again change simultaneously at
(i) 8 : 27 : 12 hrs
(ii) 8 : 32 : 24 hrs
(iii) 8 : 40 : 08 hrs
(iv) 8 : 24 : 24 hrs
Solution:
(i) 8 : 27 : 12 hrs

(e) The [HCF x LCM] for the numbers 48, 72, 108 is ……..
(i) 2472
(ii) 3680
(iii) 4090
(iv) 5184
Solution:
(iv) 5184

Case Study Based-2

Question 18.
Pollution —A Major Problem
One of the major serious problems that the world is facing today is the environmental pollution. Common types of pollution include light, noise, water and air pollution.

In a school, students thoughts of planting trees in and around the school to reduce noise pollution and air pollution.

Condition I: It was decided that the number of trees that each section of each class will plant be the same as the class in which they are studying, e.g. a section of class I will plant 1 tree a section of class II will plant 2 trees and so on a section of class XII will plant 12 trees. Condition II: It was decided that the number of trees that each section of each class will plant be the double of the class in which they are studying, e.g. a section of class I will plant 2 trees, a section of class II will plant 4 trees and so on a section of class XII will plant 24 trees.

Refer to Condition I

(a) The AP formed by sequence e. number of plants by students is ………
(i) 0, 1, 2, 3, …, 12
(ii) 1, 2, 3, 4, …, 12
(iii) 0, 1, 2, 3, …, 15
(iv) 1,2, 3, 4, …, 15
Solution:
(ii) 1, 2, 3, 4, …, 12

(b) If there are two sections of each class, how many trees will be planted by the students?
(i) 126
(ii) 152
(iii) 156
(iv) 184
Solution:
(iii) 156

(c) If there are three sections of each class, how many trees will be planted by the students?
(i) 234
(ii) 260
(iii) 310
(iv)   326
Solution:
(i) 234

Refer to Condition II

(d) If there are two sections of each class, how many trees will be planted by the students?
(i) 422
(ii) 312
(iii) 360
(iv) 540
Solution:
(ii) 312

(e) If there are three sections of each class, how many trees will be planted by the students?
(i) 468
(ii) 590
(iii) 710
(iv)  620
Solution:
(i) 468

Case Study Based-3

Question 19.
Student-Teacher Ratio

Student-teacher ratio expresses the relationship between the number of students enrolled in a school and the number of teachers in that school. It is important for a number of reasons. For example, it can be an indicator of the amount of individual attention any child is likely to receive, keeping in mind that not all class size are going to be the same.

The following distribution gives the state-wise student-teacher ratio in higher secondary schools of India (28 states and 7 UTs only).

Number of students per teacher	Number of States/ UTs	Number of students per teacher	Number of States/ UTs
15-20	3	35-40	3
20-25	8	40-45	0
25-30	9	45-50	0
30-35	10	50-55	2

(a) The mode of the above data is ………
(i) 25.5
(ii) 30.6
(iii) 35.2
(iv) 38.3
Solution:
(ii) 30.6

(b) The mean of the above data is ………….
(i) 29.2
(ii) 30.5
(iii) 38.3
(iv) 40.1
Solution:
(i) 29.2

(c) The modal class is ………..
(i) 20-25
(ii) 40 – 45
(iii) 30 -35
(iv) 50.55
Solution:
(iii) 30 -35

(d) The sum of class marks of 25-30 and 45-50 is
(i) 62
(ii)  70
(iii)  75
(iv) 85
Solution:
(iii)  75

(e) The sum of the upper and lower limits of modal class is
(i) 55
(ii) 65
(iii) 85
(iv) 75
Solution:
(ii) 65

Case Study Based-4

Question 20.
Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The ‘Skysails’ technology allows the towing kite to gain a height of anything between 100 metres to 300 metres. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a ‘telescopic mast’ that enables the kite to be raised properly and effectively.

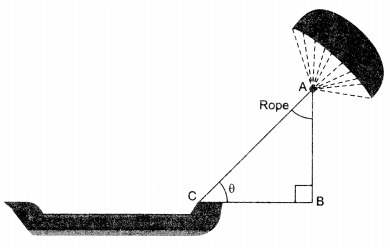
(a) In the given figures, if sin 8 = cos (30 – 30°), where 0 and 30 – 30° are acute angles, then the value of 9 is ……
(i) 30°
(ii) 60°
(iii) 45°
(iv) None of these.
Solution:
(i) 30°

(b) What should be the length of the rope of the kite sail in order to pull the ship at the angle θ (calculated in part (a) and be at a vertical height of 200 m?
(i) 300 m
(ii) 400 m
(iii) 500 m
(iv) 600 m
Solution:
(ii) 400 m

(c) If BC = 15 m, θ = 30°, then AB is ………..
(i) \(2 \sqrt{3} \mathrm{~m}\)
(ii) 15 m
(iii) 24 m
(iv)\(5 \sqrt{3} \mathrm{~m}\)
Solution:
(iv)\(5 \sqrt{3} \mathrm{~m}\)

(d) Suppose AB = BC = 12 m, then 0 = ………
(i) 0°
(ii) 30°
(iii) 45°
(iv) 60°
Solution:
(iii) 45°

(e) Given that BC = 6 m and 0 = 45°. The values of AB and AC are respectively………..
(i) AB = 4 m, AC = \(4 \sqrt{2} \mathrm{~m}\)
(ii)  AB = 7 m, AC =\(7 \sqrt{5} \mathrm{~m}\)
(iii) AB = 9 m, AC = \(9 \sqrt{3} \mathrm{~m}\)
(iv) AB = 6 m, AC =\(6 \sqrt{2} \mathrm{~m}\)
Solution:
(iv) AB = 6 m, AC =\(6 \sqrt{2} \mathrm{~m}\)

Part-B
Section-III

All questions are compulsory. In case of internal choices, attempt any one.

Question 21.
Is 7 ^x 11 ^x 13 + 11 a composite number? Justify your answer.
Solution:
Yes

Question 22.
Check whether (1,2), (3, 4), (1, 4), (2, 8) are the vertices of a square.
OR
Determine if the points (1,5), (2, 3) and (-2, -11) are collinear.
Solution:
No OR No

Question 23.
Find all zeroes of the polynomial 2x³ + x² – 6x – 3, if two of its zeroes are \(-\sqrt{3} \text { and } \sqrt{3}\)
Solution:
\(-\sqrt{3}, \sqrt{3},-\frac{1}{2}\)

Question 24.
Draw a line-segment PQ = 8.4 cm by using ruler and compass only. Find a point R on PQ such that \(\frac{3}{4}\)
Solution:
Point ‘R’ is 3.6 cm away from ‘P’.

Question 25.
If a cos θ – b sin θ = c, prove that a sin θ + b cos θ = \(\pm \sqrt{a^{2}+b^{2}-c^{2}}\)
OR
If sin θ+ sin² θ=1, then prove that cos² θ + cos⁴ θ = 1.

Question 26.
Prove that the lengths of tangents drawn from an external point to a circle are equal.

Section-IV

Question 27.
Point P divides the line segment joining the points A(2, 1) and B(5, -8) such that \(\frac{\mathrm{AP}}{\mathrm{AB}}=\frac{1}{3}\). If P lies on the line 2x -y + k O, find the value of k.
Solution:
-8

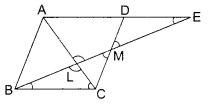
Question 28.
In the given figure. if LM || CB and LN || CD, prove that \(\frac{\mathrm{AM} {\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AD}}\)

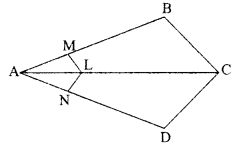
OR
In the given figure, DE || AC and DF || AE. Prove that \(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\)

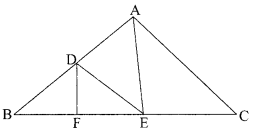
Question 29.
In the given figure, DE JI AC and DF  AE. Prove that \(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BE}}{\mathrm{EC}}\)

Solution:
7.868 cm²

Question 30.
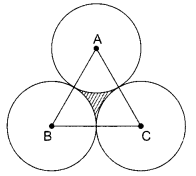
The area of an equilateral triangle is \(49 \sqrt{3} \mathrm{~cm}^{2}\). Taking each angular point as centre, a circle is described with radius equal to half the length of the side of the triangle as shown in figure. Find the area of the triangle not included in the circles.

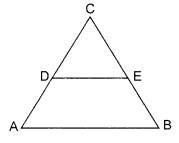
In the given figure, prove that AD = BE if ∠A = ∠B and DE || AB.

Question 31.
The weight of tea in 70 packets are as follows:

Weight (in kg)	200-201	201-202	202-203	203-204	204-205	205-206
No. of packets	12	26	20	4	2	6

Determine the modal weight.
Solution:
201.7 kg

Question 32.
Check whether the pair of equations 5x – y = 1 and are consistent. If so, solve them graphically.
Solution:
Consistent, x = 2, y = 3

Question 33.
Find the mean and median for the following data:

Class	0-10	10-20	20-30	30-10	40-50	Total
Frequency	8	16	36	34	6	100

Solution:
Mean = 26.4; Median = 27.2

Section-V

Question 34.
Two hoardings on cleanliness are kept on two poles of equal heights standing opposite to each other on either side of the road, which is 80 m wide. From a point between them on the road, the angle of elevation of the top of the poles are 60° and 30° respectively. Find the height of the pole and the distance of the point from the poles.
OR
A tree breaks down due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with it. The distance from the foot of the tree to the point where the top touches the ground is 8 metres. Find the height of the tree before it was broken.
Solution:
20√3 m; 20 m and 60 m OR 13.86 m

Question 35.
A well of diameter 3 m and 14 m deep is dug. The earth, taken out of it, has been evenly spread all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Solution:
\(\frac{9}{8} \mathrm{~m}\)

Question 36.
A part of monthly expenditure of a family is constant and the remaining varies with the price of wheat. When the price of wheat is ₹ 800 per quintals, the total monthly expenditure is ₹ 5400 and when it is ₹ 1000 per quintal, the total monthly expenditure ₹ 6000. Find the total monthly expenditure of the family when the cost of wheat is ₹ 950 per quintal. Assuming the consumption of wheat to be the same.
Solution:
₹ 5850