CBSE Sample Papers for Class 10 Maths Standard Set 5 for Practice

Students can access the CBSE Sample Papers for Class 10 Maths Standard with Solutions and marking scheme Set 5 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Set 5 for Practice

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains two parts, A and B.
2. Both Part A and Part B have internal choices.

Part-A:
1. It consists of two sections, I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.

Part-B:
1. It consists of three sections III, IV and V.
2. In section III, Question Nos. 21 to 26 are Very Short Answer Type questions of 2 marks each.
3. In section IV, Question Nos. 27 to 33 are Short Answer Type questions of 3 marks each.
4. In section V, Question Nos. 34 to 36 are Long Answer Type questions of 5 marks each.
5. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.

Part – A
Section-I

Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.

Question 1.
Given that HCF (306, 657) = 9, find LCM (306, 657).
OR
Express 429 as a product of its prime factors.
Solution :
22338 08 429 = 3 x 11×13

Question 2.
If one zero of the polynomial x² – 4x + 1 is 2 + √3 , write the other
Solution :
\(2-\sqrt{3}\)

Question 3.
State the type of the graph of the pair of linear equations: 3x – 5y =  11, 6x – 10y = 7
Solution :
Parallel lines

Question 4.
Find the value of k for which the given system has unique solution:
2x + 3y – 5 = 0, kx – 6y – 8 = 0.
Solution :
k≠- 4

Question 5.
Which term of AP: 92, 88, 84, 80 ………………. is 0?
OR
In an AP, if a = – 7.2, d= 3.6, a_n = 7.2, then find n.
Solution :
a₂₄ OR n = 5

Question 6.
Find the whole number roots of the equation 2x² – 7x + 6 = 0.
Solution :
2

Question 7.
Find the roots of x² – 2x – (r² – 1) = 0.
OR
If \(x=-\frac{1}{2}\)  is a solution of the quadratic equation 3x² + 2kx -3 = 0, find the value of k.
Solution :
1 – r , r + 1 or \(-2 \frac{1}{4}\)

Question 8.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then find ∠POA.
Solution :
50°

Question 9.
If the radii of two concentric circles are 6 cm and 10 cm, find the length of chord of the larger circle which is tangent to the other.
OR
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Solution :
16 cm OR 100°

Question 10.
Find the length of an altitude of an equilateral triangle of side 8 cm.
Solution :
\(4 \sqrt{3} \mathrm{~cm}\)

Question 11.
To divide a line segment AB in the ratio 5 : 6, a ray is drawn such that ∠B AX is an acute angle and points A₁ , A₂, A₃, so on, are located at equal distances on the ray AX. Name the point to which B is joined.
Solution :
A₁₁

Question 12.
If sin 0 = x and sec Q=y, then find the value of cot 0.
Solution :
\(\frac{1}{x y}\)

Question 13.
Find the value of \(\left(\sin ^{2} \theta+\frac{1}{1+\tan ^{2} \theta}\right)\)
Solution :
1

Question 14.
A man goes 12 m due west and then 9 m due north. How far is he from the starting point?
Solution :
15m

Question 15.
If α, β are the zeroes of a polynomial, such that α +β = 6 and αβ= 4, then write the polynomial.
Solution :
k(x² – 6x + 4)

Question 16.
A single letter is selected at random from the ‘PROBABILITY’. Find the probability that it is a vowel.
OR
Two players, Sangeeta and Reshma, play a tennis match. It is known that the probability of winning the match by Sangeeta is 0.62. What is the probability of winning the match by Reshma?
Solution :
\(\frac{1}{x y}\)

Section-II

Case Study based questions are compulsory. Attempt any four sub-parts of each question. Each sub-part carries 1 mark.

Case Study Based-1

Question 17.
Adventure Camp
Adventure camps are the perfect place for children to practice decision-making for themselves without parents and teachers guiding their every move.

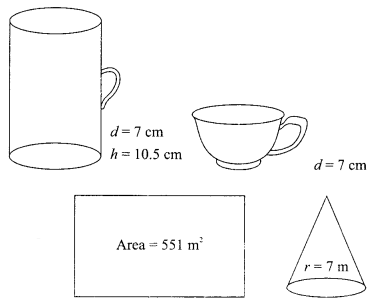
Some students of a school reached for adventure at Mukteshwar. At the camp, the waiters served some students with a welcome drink in a cylindrical glass and some students in a hemispherical cup whose dimensions are shown above.
After that they went for the jungle trek.

The jungle trek was enjoyable but tiring. As dusk fell, it was time to take shelter. Each group of four students was given a canvas of area 551 m². Each group had to make a conical tent to accommodate all the four students. Assuming that all the stitching and wasting incurred while cutting, would amount to 1 m², the students put the tents. The radius of the tent is 7 m.

Refer to Glass and Cup

(a) The volume of cylindrical cup is 1
(i) 295.75 cm³
(ii) 7415.5 cm³
(iii) 384.88 cm³
(iv) 404.25 cm³
Solution :
(iv) 404.25 cm³

(b) The volume of hemispherical cup is 1
(i) 179.67 cm³
(ii) 89.83 cm³
(iii) 172.25 cm³
(iv) 210.60 cm³
Solution :
(ii) 89.83 cm³

(c) Which container had more juice and by how much?
(i) Hemispherical cup, 195 cm³
(ii) Cylindrical glass, 207 cm³
(iii) Hemispherical cup, 280.85 cm³
(iv) Cylindrical glass, 314.42 cm³
Solution :
(iv) Cylindrical glass, 314.42 cm³

Refer to Tent

(d) The height of the conical tent prepared to accommodate 4 students is
(i) 18 m
(ii) 10 m
(iii) 24 m
(iv) 14 m
Solution :
(iii) 24 m

(e) How much space on the ground is occupied by each student in the conical tent?
(i) 54 m²
(ii) 38.5 m²
(iii) 86 m²
(iv) 24 m²
Solution :
(ii) 38.5 m²

Case Study Based-2

Question 18.
National Park
A national park is an area set aside by the government to preserve and protect the natural environment. The graph below shows a map of the National Park. The shaded areas indicate woods. The plain areas indicate meadows and fields without trees. Point O on the graph represents the location of the park’s supervisor’s office, and points P and Q are the ranger’s towers.

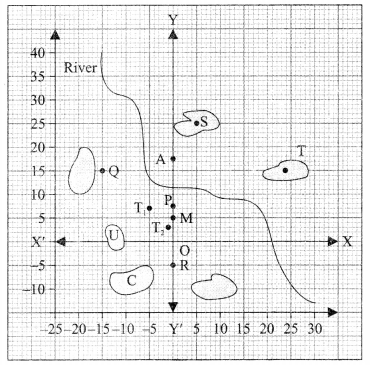
(a) What is the distance between the towers P(0, 7.5) and Q(-15, 15)?
(i) 7281.25 units
(ii) 7276 units
(iii) 9 units
(iv) 15-73 units
Solution :
(i) 7281.25 units

(b) The distance of the point S(5, 25) from x-axis is
(i) 5 units
(ii) 25 units
(iii) 1 unit
(iv) 20 units
Solution :
(ii) 25 units

(c) The point on x-axis (other than O) equidistant from the points R(Q, -5) and M(0, 5) is 1
(i) C
(ii) U
(iii) A
(iv) None of these.
Solution :
(ii) U

(d) There are two trees T₁(-5, 7) and T₂(-1, 3) in the park. The mid-point of the line segment joining both the trees is
(i) (-3,7)
(ii) (-3, 5)
(iii) (-1, 5)
(iv) (5,-3)
Solution :
(ii) (-3, 5)

(e) There is a circular pond in the park. The end points of a diameter of it are (-6, 3) and (6, 4). The coordinates of the centre of the pond is
(i) (8,-1)
(ii) (4, 7)
(iii) \(\left(0, \frac{7}{2}\right)\)
(iv) \(\left(4, \frac{7}{2}\right)\)
Solution :
(iii) \(\left(0, \frac{7}{2}\right)\)

Case Study Based-3

Question 19.
Females’ Literacy
The education of women helps to remove the social stigma that surrounds it. It is the key to eliminating social evils such as female infanticide, dowry, child marriage, harassment, etc. This will not just help the women of today but of the future generations who can live in a world where

The following distribution shows the number of literate females in the age group 0 to 60 years of a particular area.

Age (in years)	0-10	10-20	20-30	30-40	40-50	50-60
No. of literate females	350	1100	900	750	600	500

gender equality exists which ultimately raises the literacy rate.

The following distribution shows the number of literate females in the age group 0 to 60 years of a particular area.
(a) The class marks of class 40-50 is
(i) 70
(ii) 90
(iii) 10
(iv) 45
Solution :
(iv) 45

(b) The number of literate females whose ages are between 20 years and 50 years is ……
(i) 1350
(ii) 1650
(iii) 2000
(iv) 2250
Solution :
(iv) 2250

(c) The modal class of the above distribution is ……
(i) 0-10
(ii) 10-20
(iii) 20-30
(iv) 30-40
Solution :
(ii) 10-20

(d) The number of literate females whose ages are less than 40 years is ……
(i) 1450
(ii) 2350
(iii) 3100
(iv) 3700
Solution :
(iii) 3100

(e) The upper limit of modal class is …….
(i) 10
(ii) 20
(iii) 30
(iv) 60
Solution :
(ii) 20

Case Study Based-4

Question 20.
Energy Conservation
Energy conservation is the effect made to reduce the consumption of energy by using less of an energy service.
Some children of a school prepared posters on ‘Save Energy’ which are shown below.

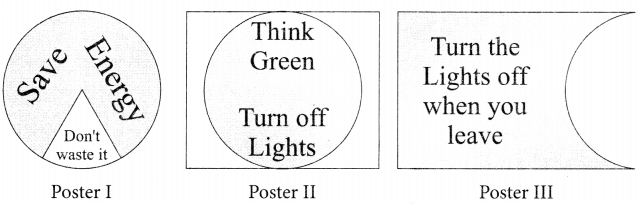
Refer to Poster I

(a) If radius of the circle is 21 cm and angle subtended by arc at centre is 60°, the length of the arc is ………                    (i) 22 cm
(ii) 28 cm
(iii) 33 cm
(iv) None of these.
Solution :
(i) 22 cm

(b) The area of sector formed by the arc (radius = 21 cm and angle of sector = 60°) is ………..
(i) 124 cm²
(ii) 231cm²
(iii) 285 cm²
(iv) 310 cm²
Solution :
(ii) 231cm²

Refer to Poster II

(c) What is the radius of circular region if length of poster is 18 cm and breadth is 14 cm?
(i) 14 cm
(ii) 18 cm
(iii) 7 cm
(iv) 9 cm
Solution :
(iii) 7 cm

(d) What is the area of circular region if length of poster is 18 cm and breadth is 14 cm?
(i) 154 cm²
(ii) 172 cm²
(iii) 196 cm²
(iv) 216 cm²
Solution :
(i) 154 cm²

Refer to Poster III

(e) The area of poster if the length and breadth of it are 18 cm and 14 cm respectively, is
(i) 155 cm²
(ii) 175 cm²
(iii) 195 cm²
(iv) 205 cm²
Solution :
(ii) 175 cm²

Part-B
Section-II

All questions are compulsory. In case of internal choices, attempt any one.

Question 21.
The length, breadth, and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm respectively. Find the length of the longest rod that can measure the three dimensions of the room exactly.
Solution :
11m ,57m

Question 22.
The centre of a circle is (2a – 1, 7) and it passes through the point (-3, -1). If the diameter of the circle is 20 units, then find the value of a.
OR
If two vertices of an equilateral triangle are (3, 0) and (6, 0), find the third vertex.
Solution :
\(\alpha=-4,2 \mathrm{OR}\left(\frac{9}{2}, \frac{3 \sqrt{3}}{2}\right)\)

Question 23.
A solid is in the form of a right circular cylinder with hemispherical ends. The total height of the solid is 58 cm and the diameter of the cylinder is 28 cm. Find the total surface area of the solid.
Solution :
5104 cm²

Question 24.
Draw a circle of diameter 8 cm. From a point P, 7 cm away from its centre, construct a pair of tangents to the circle.

Question 25.
Find the value of 2 cot² θ + 3 cosec² θ – 3, if cos 0 =\(\frac{3}{5}\)
OR
Prove that: sec² θ – cos² θ = sin² θ (sec² θ + 1).
Solution :
\(\frac{45}{16}\)

Question 26.
A circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ = \(\frac{1}{2} (perimeter of ΔABC)\). If AQ = 5 cm, find the perimeter of ΔABC.
Solution :
10cm

Section-IV

Question 27.
LCM of two numbers is 45 times of their HCF. If one of the numbers is 125 and sum of their HCF and LCM is 1150, find the other number.
Solution :
225

Question 28.
Solve for x: \(\frac{x+1}{x-1}+\frac{x-2}{x+2}=4-\frac{2 x+3}{x-2} ; x \neq 1,-2,2\)
OR
The difference of two natural numbers is 3 and the difference of their reciprocals is \(\frac{3}{28}\). Find the numbers.
Solution :
\(\frac{6}{5}\) OR 4, 7

Question 29.
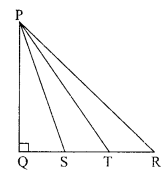
In the given figure, S and T trisect the side QR of a right triangle PQR. Prove that 8PT2 = 3PR² + 5PS².

Question 30.
Prove that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
OR
In the given figure, ΔABC and ΔXYZ are shown. If AB = 3 cm, BC = 6 cm, AC = 2y2 cm, ∠A = 80°,∠B = 60°, XY = 4√3 cm, YZ = 12 cm and XZ = 6 cm, then find the value of ∠Y.

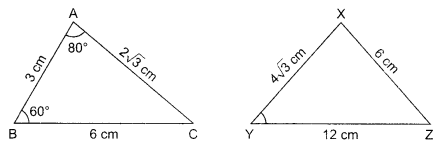
Solution :
OR 40°

Question 31.
Find the value of x from the following data ii its mode is 65, where frequency 6, 8, x and 12 are in ascending order:

Class	0-20	20-40	40-60	60-80	80-100	100-120	Mode
Frequency	6	8	X	12	6	5	65

Solution :
10

Question 32.
The angle of depression of the top and bottom of a tower as seen from the top of a 60√3 m high cliff are 45° and 60° respectively. Find the height of the tower.
Solution :
43.8m

Question 33.
For Uttarakhand flood victims, money donated by teachers of a school is shown in the following frequency distribution.

Money donated (in ₹)	500-700	700-900	900-1100	1100-1300	1300-1500
Number of teachers	4	3	18	2	3

Solution :
Mean = ₹ 980; Median = ₹ 988.88

Section-V

Question 34.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from base of the tower.       [Take √3 = 1.732]
OR
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.  [Take √3 = 1.732]
Solution :
2.5 m, 4.33 m OR 73.2 m

Question 35.
Given that the zeroes of the cubic polynomial x³ – 6x² + 3x + 10 are of the form a, a + b, a + 2b for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.
Solution :
a = – 1, 5 ; b = 3, -3 ; -1, 2, 5

Question 36.
A part of monthly Hostel charge is fixed and the remaining depends on the number of days one has taken food in the mess. When Swati takes food for 20 days, she has to pay ₹ 3000 as hostel charges whereas, Mansi who takes food for 25 days pays ₹ 3500 as hostel charges. Find the fixed charges and the cost of food per day.
Solution :
₹ 1,000; ₹ 100