Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 5 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 5 for Practice
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study-based questions.
![]()
Question 1.
If the mean of numbers 2, a, 6 and 7 is 15 and the mean of numbers 6, 18 1, a, b is 20, then find the value of b.
OR
Consider the following distribution:
| Class | 0-15 | 15-30 | 30-45 | 45-60 |
| Frequency | 5 | 9 | 11 | 15 |
Find the median class of the distribution. (2)
Answer:
Given: Mean of 2, a, 6 and 7 is 15.
∴ \(\frac{2+a+6+7}{4}\) = 15
⇒ 15 + a =60
⇒ a = 45 ………………………………. (i)
Also, mean of 6, 18, 1, a and b is 20.
∴ \(\frac{6+18+1+a+b}{5}\) = 20
⇒ 25 + a + b = 100
⇒ 25 + 45 + b = 100 [From (i)]
⇒ b = 100 – 70
⇒ = 30
Hence, the value of b is 30.
OR
| Class | 0-15 | 15-30 | 30-45 | 45-60 |
| Frequency | 5 | 9 | 11 | 15 |
| Cumulative Frequency | 5 | 5 + 9 = 14 | 14+11 = 25 | 25+15 = 40 |
Hence, sum of frequencies, N = 40
∴ \(\frac{N}{2}\) = 20
Cumulative frequency just greater than 20 is 25, which belongs to class 30-45.
∴ Median class = 30 – 45
![]()
Question 2.
Solve the following quadratic equation for x : 9x2 – 6b2x – (a4 – b4) = 0. (2)
Answer:
Let
We have,
9x2 – 6b2x – (a4 – b4) = 0
Using quadratic formula,

Question 3.
Find the 23rd term of the A.P. -4\(\frac{1}{2}\), -3, -1\(\frac{1}{2}\)….. (2)
Answer:
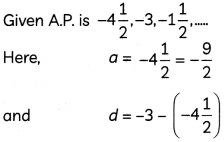

Concept Applied
The nth term of an A.P. is given as an = a + (n – 1) d.
![]()
Question 4.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
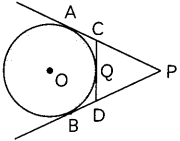
Answer:
We know, tangents drawn from an external point to a circle are equal in length.
∴ PA = PB, CA = CQ, DQ = DB
Now,
PC + PD = (PA – AC) + (PB – BD)
= (PA – QC) + (PA – QD)
[∵ AC = QC, PB = PA, BD = QD]
= (12 – 3) + (12 – 3)
= 18 cm
Question 5.
Find the missing frequency x of the following distribution, if mode is 34.5.
| Marks obtained | Number of students |
| 0-10 | 4 |
| 10-20 | 8 |
| 20-30 | 10 |
| 30-40 | X |
| 40-50 | 8 |
Answer:
Given: Mode = 34.5
Modal class = 30 – 40
We know,
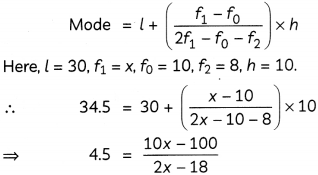
⇒ 4.5 (2x – 18) = 10x – 100
⇒ 10x – 9x = 100 – 81
⇒ x = 19
Hence, the value of missing frequency x is 19
![]()
Question 6.
An A.P. consists of 50 terms. If its 3rd and last terms are 12 and 106, respectively, find the 29th term.
OR
Resham created an A.P. whose five times of the fifth term is equal to ten times its 10th term. Show that 15th term of the A.P. is zero. (2)
Answer:
Let a be the first term and d be the common difference of the A.P.
Then, a3 = 12
⇒ a + 2d = 12 …………………………….(i)
and last term, l = 106
⇒ a50 = 106
[∵ There are 50 terms in A.P.]
⇒ a + 49d = 106 ………………………………(ii)
Solving equations (i) and (ii), we get
d = 2, a = 8
So, 29th term, a29 = a + 28d
= 8 + 28 x 2
= 64
Hence, 29th term of the A.P. is 64.
Caution
Since there are 50 terms in the A.P, so 106 will be 50th term of the A.P.
OR
Let a be the first term and d be the common difference of the A.P.
Then, 5a5 = 10a10 (Given)
⇒ 5 (a + 4d) = 10 (a + 9d)
⇒ 5a + 20d = 10a + 90d
⇒ -5a = 70 d
⇒ a = -14d ………………………………(i)
Now, 15th term = a15
= a + 14d
= -14d + 14d [From (i)]
= 0
So, 15th term of the A.P. is zero.
Hence, proved.
![]()
SECTION – B
(12 Marks)
Question 7.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively, is melted and recast into a cone of base diameter 8 cm. Find the height of the cone. (3)
Answer:
Let the height of the cone be H cm.
Then, volume of spherical shell = volume of cone
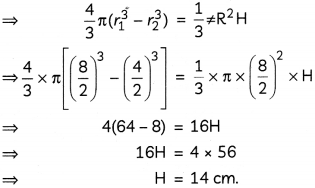
Hence, height of the cone is 14 cm.
Question 8.
A statue 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and the angle of elevation of the top of pedestal is 45°. Find the height of the pedestal. [Use \(\sqrt{3}\) = 1.73]. (3)
Answer:
Let AB be the statue which is standing on the top of pedestal BC and P be the point of observation on the ground.
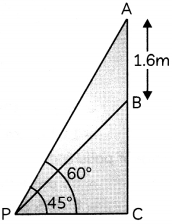

Hence, height of the pedestal is 2.184 m.
![]()
Question 9.
A solid is composed of a cylinder with hemispheres attached on both ends, as shown in the figure. If the whole length of the solid is 108 cm and diameter of the hemispherical ends is 35 cm, find the cost of polishing its surface at the rate of 55 paise per cm2. (3)
Answer:

Here,
Height of cylindrical part (h)
= Total length – 2 × Radius of hemispherical part.
= 108 – 2 × \(\left(\frac{35}{2}\right)\)
= 73 cm
∴ CSA of solid = CSA of cylinder + 2 × CSA of hemisphere
= 2πrh + 2 x (2πr2)
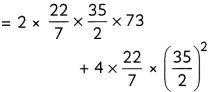
= 8030 + 3850
= 11880 cm2
Now, Rate of polishing
= 55 paise per cm2
= ₹ 0.55 per cm2
Total cost of polishing
= Rate x CSA of solid
= 0.55 x 11880
= ₹ 6534
![]()
Question 10.
In the given figure, PQ is a chord of a circle and PT is a tangent touching the circle at P, such that ∠QPT = 60°. Find the measure of ∠PRQ.
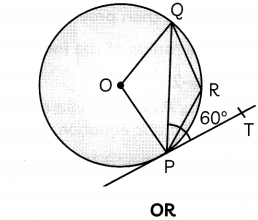
Draw a line segment PQ of length 7.2 cm and divide it in the ratio 4 : 7. Also, measure the two parts. (3)
Answer:
We have,

We know, angle subtended by an arc at the centre is double the angle subtended by it on circumference of the circle.
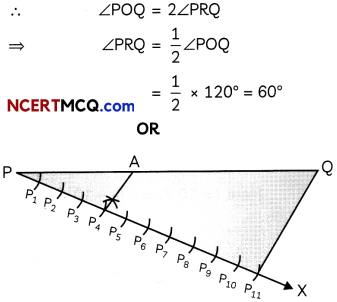
Steps of construction:
- Draw a line segment PQ of length 7.2 cm.
- From point P, draw a ray PX such that ∠QPX is acute.
- On ray PX, mark 4 + 7 i.e. 11 points, namely, P1, P2, …….P11 at equal distances.
- Join P11Q.
- From point P4, draw a line P4A, parallel to P11Q, intersecting PQ at A.
Thus, point A divides PQ in the ratio 4 : 7.
So, PA = 2.62 cm and QA = 4.58 cm.
![]()
SECTION – C
(16 Marks)
Question 11.
In a class test, marks obtained by 120 students are given in the following frequency distribution.
| Marks | Number of students |
| 0-10 | 1 |
| 10-20 | 3 |
| 20-30 | 7 |
| 30-40 | 10 |
| 40-50 | 15 |
| 50-60 | X |
| 60-70 | 9 |
| 70-80 | 27 |
| 80-90 | 18 |
| 90 -100 | y |
If mean marks of the students is 59, then find the values of x and y. (4)
Answer:
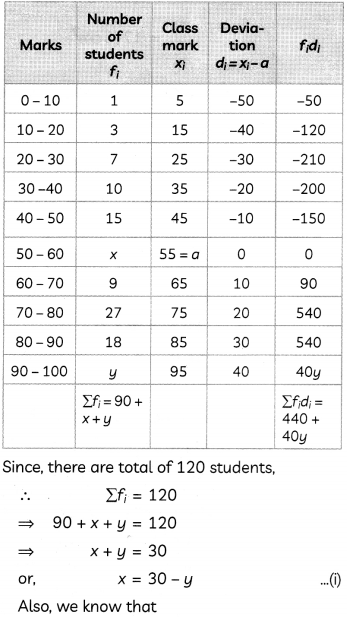
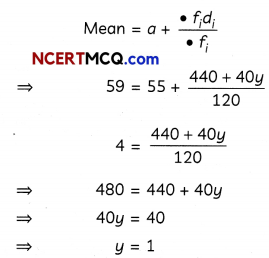
Putting the value of y in eq. (i), we get
x = 30 – 1
= 29
Hence, the values of x and y are 29 and 1 respectively.
![]()
Question 12.
An airplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the airplane of two points on both banks of a river in opposite direction of the plane, are 45° and 60° respectively. Find the width of the river. [Use \(\sqrt{3}\) = 1.732]
OR
A boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 30°. A girl standing on the roof of a 20 m high building, finds the elevation of the same bird to be 45°. If the boy and the girl are on the opposite sides of the bird, find the distance of the bird from the girl. [Use \(\sqrt{2}\) = 1.414]. (4)
Answer:
Let A be the position of aeroplane in the sky and AB be its vertical height. Also, let P, Q be the two points on both banks of the river.
∴ AB = 300 m, ∠XAP = ∠APB = 45°, ∠YAQ = ∠AQB = 60°
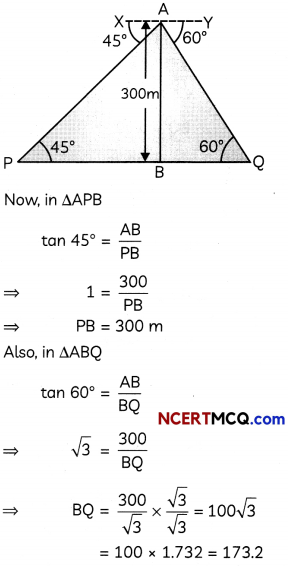
So, width of river = PQ = PB + BQ
= 300 + 173.2
= 473.2
Hence, width of the river is 473.2 m.
OR
Let P be the position of the boy, B be the position of bird and Q be the position the girl standing on the roof of building QM.
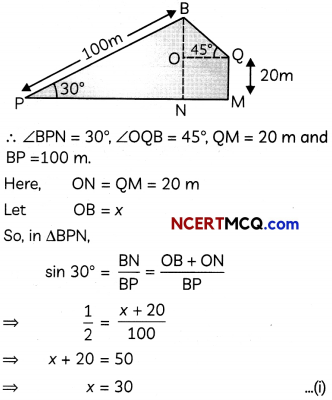
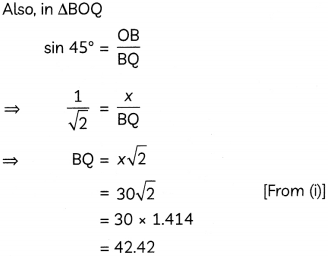
Hence, distance of the bird from the girl is 42.42 m.
![]()
Question 13.
Case Study-1
Toy blocks are wooden or plastic or foam pieces of various geometrical shapes and colors that are used for constructing other shapes and figures.
Kareem’s younger cousin was playing with the blocks which consists of different shapes. He saw that his cousin has put a circular block into a hollow triangular block and the two blocks perfectly fit each other.

It reminds him a question, in which a circle is inscribed in a DABC such that the sides BC, AC and AB touches the circle at points D, E and F respectively.
If length of sides AB, BC and AC are 9 cm, 8 cm and 7 cm respectively then, answer the following questions.
(A) If AB = AC, then prove that BD = DC. (2)
(B) Find the radius of the incircle. (2)
Answer:
(A) We know, tangents drawn from an external point to a circle are equal in length.
∴ AF = AE, BF = BD, CD = CE [Given]
Now, AB = AC
⇒ AF + BF = AE + EC
⇒ BF = EC [∵ AF = AE]
⇒ BD = DC
[∵ BF = BD, EC = DC]
Hence, proved.
(B) We have,
AB = 9 cm, BC = 8 cm and AC = 7 cm
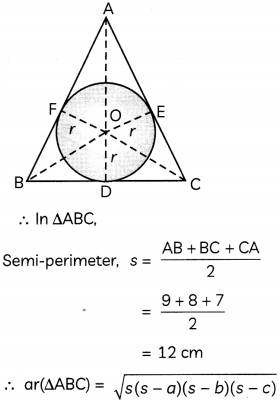
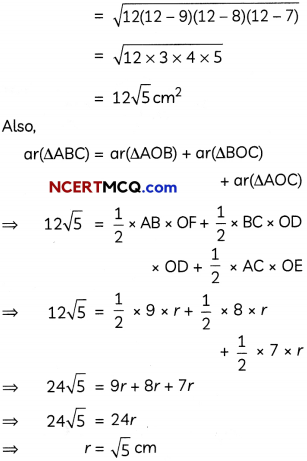
Hence, radius of the circle is \(\sqrt{5}\) cm.
![]()
Question 14.
Case Study-2
Two students, Paul and Shree, of Class X while solving a quadratic equation, committed the

following mistakes. Paul made a mistake in the constant term and get the roots as 6 and 8. While Shree committed an error in the coefficient of x and got the roots as 3 and 14
Based on the above information answer the following questions.
(A) Find the correct quadratic equation. (2)
(B) Write the discriminant and nature of roots of the correct quadratic equation. (2)
Answer:
(A) Since, Paul made mistake in writing the constantterm ofthe equation, so its coefficient of x must be correct.
∴ Correct sum of roots = 6 + 8 = 14
Similarly, Shree made mistake in writing the coefficient of x of the equation, so its constantterm must be correct.
∴ Correct product of roots = 3 x 14 = 42
So, the correct quadratic equation is:
x2 – (sum ofroots)x+product of roots = 0
⇒ x2 – 14x + 42 = 0
(B) From part (A), the correct quadratic equation is: x2 – 14x + 42 = 0
∴ Discriminant = b2 – 4ac
Here, a = 1, b = -14, c = 42
∴ Discriminant = (-14)2 – 4 x 1 x 42
= 196 – 168
= 28
Since, value of discriminant is greater than zero, so the nature of roots is real and unequal.