CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 2 for Practice

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.
2. All questions are compulsory.
3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
5. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study-based questions.

SECTION – A
(12 Marks)

Question 1.
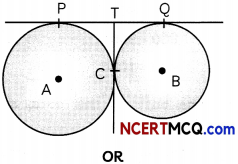
In the given figure, two circles touch each other at the point C. Prove that the common tangent to the circles at C, bisects the common tangent at P and Q.

AB is a tangent to a circle with centre O and radius 4 cm, at point A. If AOB is an isosceles triangle, then find the distance of the point B from the centre of the circle. (2)
Answer:
We know, tangents drawn from an external point to a circle are equal in length.
So, for a circle with centre A,
TP = TC ………………………………… (i)
And, for a circle with centre B,
TC = TQ ………………………………… (ii)
From (i) and (ii),
we have
TP = TQ
⇒ T is the mid-point of PQ.
Hence, TC bisects PQ.
Hence, proved.
OR
Given: ΔAOB is an isosceles triangle.
Also, ∠OAB = 90° [∵ Tangent ⊥ Radius]
So, OB is the hypotenuse, and OA = AB = 4 cm
∴ Using Pythagoras theorem,

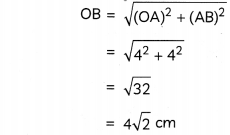
Hence, distance of the point B from the centre of the circle is 4\(\sqrt{2}\) cm.

Question 2.
If the area of base of a cone is 770 cm² and its curved surface area is 814 cm², find the slant height of the cone. (2)
Answer:
Let radius of base of cone be r cm. Now, according to the question,

Hence, slant height of the cone is 7.4\(\sqrt{5}\)

Question 3.
Neha wrote 30 numbers in her notebook, whose mean is 18. If she increased each number by 1, what is the new mean? (2)
Answer:
Given: Mean of 30 numbers = 18
∴ Sum of 30 numbers = 18 x 30
= 540

Since, each observation is increased by 1.

So. sum of total of 30 observations wiLl be increased by (1 + 1 + 1 + 1 ……. 30 times) i.e. 30.
∴ Newsum = 540 + 30
= 570
∴ New mean = \(\frac{570}{30}\)
Hence, the new mean is 19.

Related Theory

Shortcut Method: If the mean of a given set of data is x, and each observation is increased by a fixed number a, then new mean = x + a.

Question 4.
Find the relation between a, b and c if the roots of the quadratic equation (a – b)x² – (b – c) x + c – a = 0 are equal. (2)
Answer:
Given equation is
(a – b)x² – (b – c)x + c – a = 0
∴ A = (a – b), B = -(fa – c), C = c – a
Since, the given equation has equal roots
∴ Discriminant =0
⇒ B² – 4AC = 0
⇒ [-(b – c)]² – 4 x (a – b) x (c – a) = 0
⇒ (b²-2bc + c²) – 4 (ac – a² – bc + ab) = 0
⇒ 4a² + b² + c² – 4ab + 2be – 4ac = 0
⇒ (-2a)² + b² + c² + 2 x (-2a) xb + 2xbxc + 2 x (-2a) x c = 0
⇒ (-2a + b + c)²=0
⇒ -2a + b + c = 0
⇒ b + c = 2a
which is the required relation between a, fa and c.

Question 5.
In an A.P., the first term is 12 and the common difference is 6. If the last term of the A.P. is 252, find its middle term. (2)
Answer:
We have, a = 12, d = 6 and l = 252.
Let there be n terms in the A.P.
Then, l = a + (n – 1) d
⇒ 252 = 12 + (n – 1)6
⇒ 6(n – 1) = 240
⇒ n – 1 = 40
⇒ n = 41

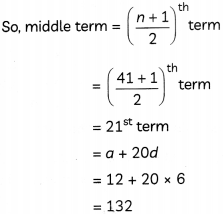
Concept Applied
If n is odd, then

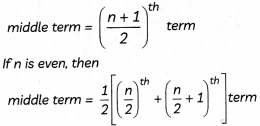
Question 6.
Find the median of the following data:
9, 7, 6,11, 15, 8, 7, 4, 10
OR
Compute the mode for the following frequency distribution: (2)

Size of items (in cm)	Frequency
0-4	5
4-8	7
8-12	9
12-16	17
16-20	12
20-24	10
24-28	6

Answer:
Arranging the given data in ascending order, we get
4, 6, 7, 7, 8, 9, 10, 11, 15
Here, number of terms (n) = 9 i.e. odd

Hence, median of the data is 8.

Caution
w Before applying the formula of median, always arrange the given set of data in ascending order.
OR
Here, maximum frequency = 17
And, class with maximum frequency is 12 – 16.
∴ Modal class = 12 – 16
We know,

Hence, the mode of given frequency distribution is 14.46.

SECTION – B
(12 Marks)

Question 7.
Draw a line segment AB of length 6 cm and mark a point X on it such that bx = \(\frac{4}{5}\) AB. (2)
Answer:
We have,


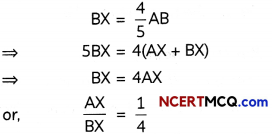
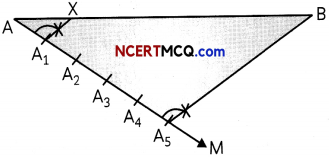
Steps of construction:

1. Draw a line segment AB of length 6 cm.
2. From point A, draw a ray AM such that ∠BAM is acute.
3. On ray AM, mark 1 + 4 i.e. 5 points namely, A₁, A₁, A₃, A₄, A₅ at equal distances.
4. Join A₅B.
5. From point Alf draw a line A₁X, parallel to A₅B, intersecting AB at X.

Thus, point X divides AB in the ratio 1: 4.

Question 8.
Solve for x:
\(\frac{x+1}{x-1}+\frac{x-2}{x+2}=4-\frac{2 x+3}{x-2}, x \neq 1,-2,2\) (3)
Answer:
We have,

Question 9.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (3)
Answer:
Let AB be the building and CD be the cable tower.


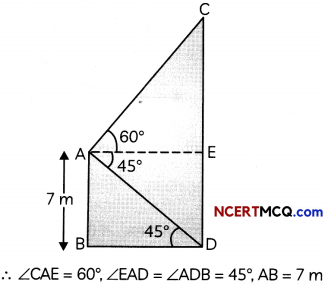
Hence, height of the cable tower is 7(\(\sqrt{3}\) + 1)m.

Caution
If the values of \(\sqrt{3}, \sqrt{2}\) ore not specified in the question, you may leave your final answer in terms of \(\sqrt{3}, \sqrt{2}\).

Question 10.
The eighth term of an A.P. is half its second term and the 11^th term exceeds one-third of the fourth term by 1. Find the sum of its first 13 terms.
OR
David started work in the year 1995 at an annual salary of ₹ 5000 and received an increment of ₹ 300 each year. In which year did his income reach 8000? (3)
Answer:
Let a be the first term and d be the common difference of the A.P.
Now, a₈ = \(\frac{1}{2}\)a₂
or, 2a₈ = a₂
⇒ 2(a + 7d) = a + d
⇒ a + 13d = 0 ………………………………………… (i)
⇒ 5x (x + 5) – 6(x + 5) = 0 =* (5x – 6) (x + 5) = 0

Also,
a₁₁ – \(\frac{1}{3}\)a₄ = 1
or, 3a₁₁ – a₄ = 3
⇒ 3(a+ 10d) – (a + 3d) = 3
⇒ 2a + 27d = 3 …………………………………………….. (ii)
Solving equations (i) and (ii), we get a = -39, d = 3
Now, sum of first 13 terms

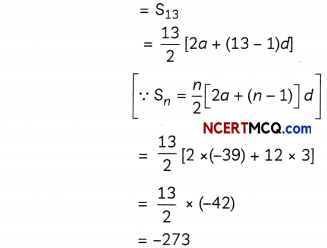
OR
Since, annual salary of David increases uniformly by a constant amount every year, so, his salary every successive year forms an A.P. with a = ₹ 5000, d = ₹ 300.
Let ₹ 8000 be the salary of David in the n^th year.

Then, a_n = 8000
⇒ a + (n – 1)d = 8000
⇒ 5000 + (n – 1) x 300 = 8000
⇒ 300(n – 1) = 3000
⇒ (n – 1) = 10
⇒ n = 11
Since, 1995 + 11 = 2006, so in the year 2006,
David’s income would reach ₹ 8000.

SECTION – C
(16 Marks)

Question 11.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point at contact C is intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.

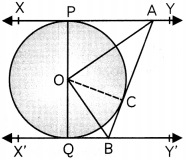
Answer:
Given: XY, X’Y’ and AB are tangents to a circle with centre O at points P, Q and C respectively.

To prove: ∠AOB = 90°

Proof: We know, tangents drawn from an external point to a circle are equal in length.
∴ AP = AC ………………………………… (i)
[Tangents from point A]. and BC = BQ ………………………………… (ii)
[Tangents from point B]

Now, in ΔAOP and AOC
AP = AC [From (i)]
OP = OC [Radii]
OA = OA [Common side]
∴ ΔAOP ≅ ΔAOC
[SSS congruency rule]
∴ ∠AOP = ∠AOC [c.p.ct.] ………………………………… (iii)
Similarily,
ΔBOC ≅ ΔBOQ
∴ ∠BOC = ∠BOQ ………………………………… (iv)

Now,
∠POA + ∠AOC + ∠BOC + ∠BOQ = 180° [Linear pair]
⇒ ∠AOC + ∠AOC + ∠BOC + ∠BOC = 180°
[From (iii),(iv)]
⇒ 2(∠AOC + ∠BOC) = 1800
⇒ 2(∠AOB) = 1800
or, ∠AOB = 90°

Hence, proved.

Question 12.
The dimensions of a solid iron cuboid are 4.4 m x 2.6 m x 1 m. It is melted and recast into a hollow cylindrical pipe of inner radius 30 cm and thickness 5 cm. Find the length of the pipe.
OR
The internal and external diameters of a hollow hemispherical vessel are 24 cm and 25 cm, respectively. If the cost to paint 1 cm² of the surface is 5 paise, find the total cost of painting the vessel all over. (4)
Answer:

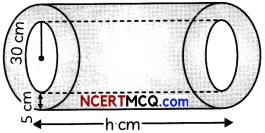
Internal radius of pipe (r) =30 cm and, its thickness = 5 cm
∴ External radius of pipe (R)
= 30 + 5 = 35 cm
Let length of the pipe be h cm.
Then,
Volume of iron in cuboid = Volume of iron in the pipe
⇒ 440 x 260 x 100 cm³ = n(R² – r²)h
⇒ 440 x 260 x 100 = \(\frac{22}{7}\) x [(35)² – (30)²] x h
⇒ 440 x 260 x 100 = \(\frac{22}{7}\) (65 x 5) x h
[∵ a² – b² = (a + b) (a – b)]
\(h=\frac{440 \times 260 \times 100 \times 7}{22 \times 65 \times 5}\)
= 11200 cm
Hence, length of the pipe is 11200 cm, or 112 m.

OR

Given:
Internal diameter = 24 cm and, external diameter = 25 cm

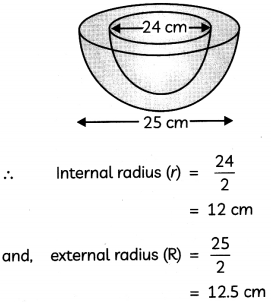
Now, total area to be painted
= CSA of outer part of hemisphere + CSA of inner part of hemisphere + Area of ring base = 2πR² + 2πr² + π(R² – r²)
= 2 x π x (12.5)² + 2 x π x (12)² + n [(12.5)² – (12)²]
= 312.5π + 288π + 12.25π
= 6 1 2.75π
= 612.75 x 3.14
= 1924.035 cm²

Now,
Rate of painting = 5 paise per cm²
= ₹ 0.05 per cm²
∴ Total cost of painting = Rate x Area
= 0.05 x 1924.035
= ₹ 96.2

Question 13.
Case Study-1
An electric meter is a device that measures that amount of electricity consumed by a house, office, factory or any building over a period of time.

A data was recorded regarding the monthly consumption of electricity in a locality in which 100 families resides. The data is tabulated below.

Monthly consumption (in kWh)	Number of families
0 -100	2
100 – 200	5
200 – 300	X
300 – 400	12
400 – 500	17
500 – 600	20
600 – 700	y
700 – 800	9
800 – 900	7
900 -1000	4

On the basis of this data, answer the following question.
(A) If the median monthly consumption of electricity is 525 kWh, then find the values of x and y. (2)
(B) Find the average monthly consumption of electricity by the families of this locality. (2)
Answer:
(A)

Class Interval	Frequency	Cumulative Frequency
0-100	2	2
100-200	5	7
200-300	X	7 + x
300-400	12	19 +x
400 – 500	17	36 + x
500 – 600	20	56 + x
600 – 700	y	56 + x + y
700-800	9	65 + x + y
800 – 900	7	72 +x + y
900 – 1000	4	76 + x + y
	N = 100

Since, sum of frequencies = 100
⇒ 2 + 5 + x + 12 + 17 + 20 + y + 9 + 7 + 4
= 100
⇒ 76 + x + y = 100
⇒ x + y = 24 ………………………………….. (i)
∵ Median = 525 [Given]
∴ Median class = 500 – 600

We know,
Median = l + \(\left(\frac{\frac{N}{2}-c f}{f}\right)\) x h

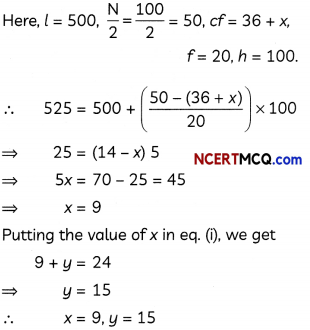
(B)

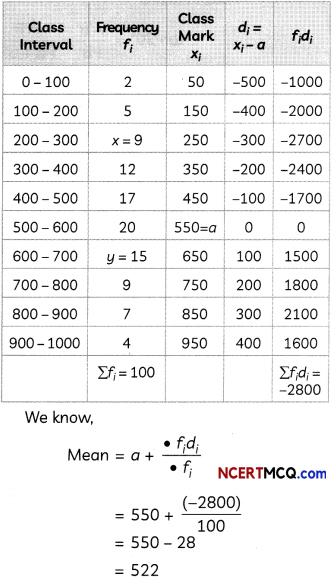
Hence, the average monthly consumption of electricity is 522 kwh.

Question 14.
Case Study-2
An inclinometer is an instrument which is used for measuring angles of slope, elevation or depression of an object, with respect to gravity’s direction.

The angle of elevation of an aeroplane from a point P on the ground is 45°. After flying for 15 seconds, the angle of elevation changes to 30°. If the aeroplane is flying at a constant height of 2500 m, then answer the following questions:

(A) Draw a labelled figure on the basis of the given information and calculate the distance covered by the plane during the period of observation. (2)

(B) What is the average speed of the aeroplane? [Use \(\sqrt{3}\) = 1.73]
Answer:

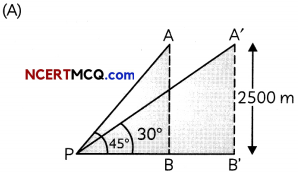
Here A is the initial position of the aeroplane and AB is its vertical height. Similarly, A’ is the position of the aeroplane after 15 seconds and A’B’ is its vertical height.

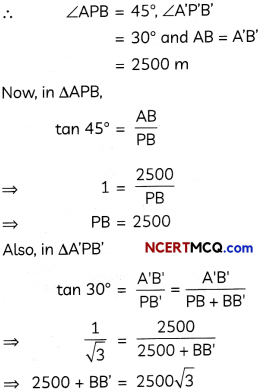
⇒ BB’ = 2500(\(\sqrt{3}\) – 1)m
So, distance covered by the plane during the period of observation
= A’A = B’B
= 2500(\(\sqrt{3}\) – 1)m

(B) We have,
Distance A’A = 2500 (\(\sqrt{3}\) – 1)m and Time taken = 15 sec
∴ Speed of the plane

Hence, the average speed of the aeroplane is 121.67 m/sec.