CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 3 with Solutions

Students can access the Online Education CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

Online Education CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 3 for Practice

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.
2. All questions are compulsory.
3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
5. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study-based questions.

SECTION – A
(12 Marks)

Question 1.
If two tangents, inclined to each other at an angle of 60°, are drown to a circle of radius 3 cm, then find the length of each tangent.
OR
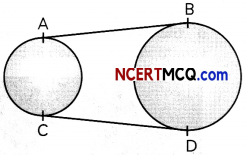
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.

Answer:



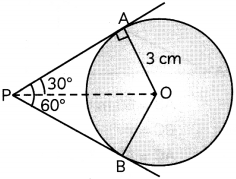
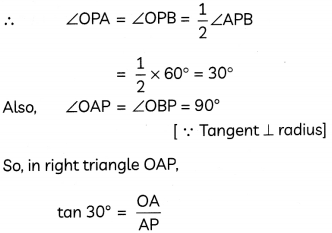
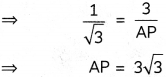
Hence, the length of each tangent is 3\(\sqrt{3}\)cm.

OR

Given: AB and CD are common tangents to two circles of unequal radii.

To prove: AB = CD

Construction: Extend BA and DC, so that they meet at point P.

Proof: We know, tangents drawn from an external point to a circLe are equal in Length.

So, for smaller circle,
PA = PC ……………………………………… (i)
And, for bigger circle,
PB = PD ……………………………………… (ii)

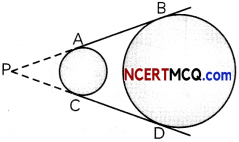
Subtracting (i) from (ii), we get
PB – PA = PD – PC
⇒ AB = CD

Hence, proved.

Question 2.
A 1.6m tall girl stands at a distance of 3.2m from a lamp post and casts a shadow of 4.8m on the ground. find the height of the lam past. (2)
Answer:
Let AB be the girl and BM be its shadow. Similarly, let PQ be the lamp post and QM be its shadow. Also, Let θ be the angle of elevation of the Sun.


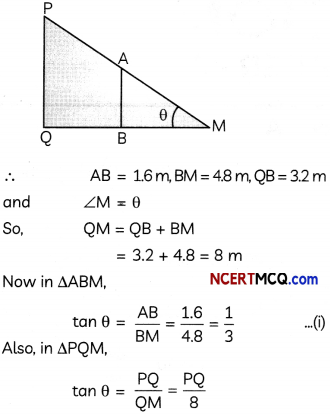
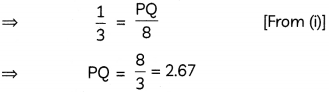
Hence, height of the lamp post is 2.67m.

Question 3.
From a solid cube of side 7 cm, a conical cavity of diameter 6 cm and height 7 cm is hollowed out. Find the volume of the remaining solid. (2)
Answer:
Volume of remaining solid = Volume of cube – Volume of the cone

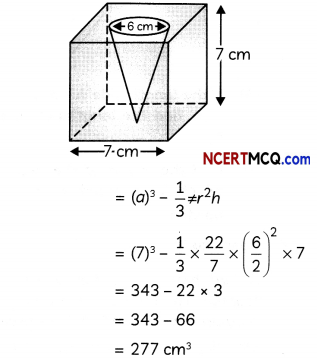
Question 4.
Mr. Biswal, a class teacher of class X, prepared a table on the number of days his students missed the school during the term-1 of session 2021-22. Following data was recorded.

Number of absent days	Number of students
0-5	2
5-10	6
10-15	9
15-20	7
20-25	4

Convert this frequency distribution to a more than type cumulative frequency distribution table.
Answer:

Class	Cumulative Frequency
More than 0	2 + 6 + 9 + 7 + 4 = 28
More than 5	6 + 9 + 7 + 4 = 26
More than 10	9 + 7 + 4 = 20
More than 15	7 + 4 = 11
More than 20	4

Question 5.
A portion of 60 m long tree is broken by tornado and the top struck up the ground making an angle of 30° with the ground level. Find the height of broken part of the tree. (2)
Answer:
Let AB be the tree and C be the point on it, from where it is broken, so that the top A of the tree touches the ground at point A’.

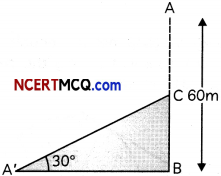
∴ AB = 60 m, ∠CA’B = 30°
Let BC = x
Then, AC = AB – BC = 60-x
∴ A’C = AC = 60 – x
Now, in ΔA’BC

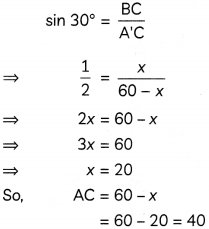
Hence, the height of broken part of the tree is 40 m.

Question 6.
If the mean of the following data is 2.6, then find the missing frequency p.

x1	1	2	3	4	5
f1	4	5	p	1	2

OR
Find the mode of the following frequency distribution:

Class Interval	Frequency
25-30	25
30-35	34
35-40	50
40-45	42
45-50	38
50-55	14

Answer:

xi	fi	Σfixi
1	4	4
2	5	10
3	P	3P
4	1	4
5	2	10
	Σfi = 12 + p	Σfixi = 28 + 3p

We know, Mean = \(\frac{f_{i} x_{i}}{f_{i}}\)
⇒ \(2.6=\frac{28+3 p}{12+p}\)
⇒ 2.6(12 + p) = 28 + 3p
⇒ 3p – 2.6p = 31.2 – 28
⇒ 0.4p = 3.2
⇒ p = 8
Hence, the value of p is 8.
OR
Here, maximum frequency = 50
And, class with maximum frequency is 35 – 40.
∴ Modal class = 35 – 40

We know,
Mode = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) x h
Here, l = 35, f₁ = 50, f₀ = 34, f₂ = 42, h = 5.
∴ Mode = 35 + \(\left(\frac{50-34}{100-34-42}\right) \times 5\)
= 35 + \(\frac{16}{24}\) x 5
= 35 + 3.33
= 38.33
Hence,the mode of given frequency distribution is 38.33.

SECTION – B
(12 Marks)

Question 7.
Solve for x:
1 + 4 + 7 + 10 + …. + x = 287 (3)
Answer:
We have, 1 + 4 + 7 + 10 + ….. + x = 287
Here, the series 1,4, 7,10, ….. x forms an A.P.
with a = 1, d = 4 – 1 = 3 and l = x.
Let there be n terms in this A.P.
We know, sum of n term of an A.P. is given as
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
⇒ 287 = \(\frac{n}{2}\) [2 x 1 + (n – 1) x 3]
⇒ 574 = n(3n – 1)
⇒ 3n² – n – 574 = 0
⇒ 3n² – (42 – 41) n – 574 = 0
⇒ 3n² – 42n + 41n – 572 = 0
⇒ 3n(n – 14) + 41(n – 14) = 0
⇒ (3n + 4) (n – 14) = 0
⇒ n = \(\frac{-4}{3}\), 14
Since, number of terms cannot be in fraction or negative
∴ n = 14
∴ a₁₄ = x
⇒ a + 13d = x
⇒ 1 + 13 x 3 = x
⇒ x= 40
Hence, the value of x is 40.

Question 8.
Draw a circle of any radius and unknown centre. Take a point P outside the circle and construct a pair of tangents from this point to the circle. (3)
Answer:

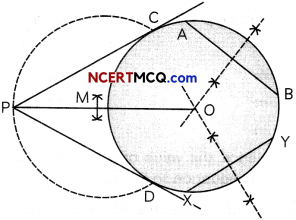
Steps of construction:

1. Draw a circle of any radius and unknown centre.
2. Draw two non-parallel chords AB and XY on the circle, drawn in step (1).
3. Draw perpendicular bisectors of AB and XY. Let these two perpendicular bisectors intersect each other at point O. Thus, 0 is the centre of the circle.
4. Take a point P outside the circle and join OP.
5. Draw perpendicular bisector of OP to get its mid-point M.
6. Taking M as centre and MO = MP as radius, draw a circle which intersects the circle, drawn in step (1), at points C and D.
7. Join PC and PD.

Thus, PC and PD are the required tangents to the circle with centre O.

Concept Applied
Perpendicular bisector of a chard of a circle passes through its centre. So, perpendicular bisectors of chords AB and XY intersect each other at centre of the circle.

Question 9.
Find the value of p for which the quadratic equation (p + 1) x² – 6(p + 1) x + 3(p + 9) = 0, p ≠ -1, has equal roots. Hence, find the roots of the equation. (3)
Answer:
Given equation is:
(p + 1) x² – 6(p + 1)x + 3(p + 9) = 0 …………………………………… (i)
Since, the equation has equal roots
∴ Discriminant = 0
⇒ b² – 4ac = 0
Here, a = (p + 1), b = -6(p + 1), c = 3(p + 9)
[-6(p + 1)]² – 4 x (p + 1) x [3(p + 9)] = 0
∴ (p + 1) [36(p + 1) – 12(p + 9)] = 0
⇒ 36p + 36 – 12p – 108 = 0
[∵ p ≠ -1 (Given)]
⇒ 24p – 72 = 0
⇒ P = \(\frac{72}{24}\)
= 3
Putting p = 3 in equation (i), we get
4x² – 24x + 36 = 0
⇒ x² – 6x + 9 = 0
⇒ (x – 3)² = 0
⇒ x = 3, 3
Hence, the value of p is 3 and the roots of the equation so formed are 3 and 3.

Question 10.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree, standing on opposite bank of the river, is 60°. When he moves 40 m away from the bank, he finds angle of elevation to be 30°. Find the width of the river and the height of the tree.
OR
The shadow of a pole is three times as long as the shadow of the pole when the Sun rays meet the ground at an angle of 60°. Find the angle between the Sun rays and the ground at the time of longer shadow. (3)
Answer:
Let AB be the tree, PB be the river and P’ be the final position of the person.

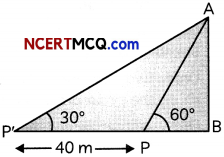
Putting PB = 20 in (i), we get
AB = 20\(\sqrt{3}\)
Hence, width of the river is 20 m and height ofthetreeis 20\(\sqrt{3}\)m.
OR
Let AB be the pole, BC be its shadow when angLe of elevation of the Sun is 60° and BD be its longer shadow.

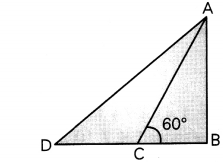
So, according to the question
BD = 3BC ……………………………….. (i)
Let the angle between Sun rags and the ground at the time of longer shadow be O.

Now, in ΔABC

Hence, the required angle is 30°.

SECTION – C
(16 Marks)

Question 11.
Find mean and median of the following frequency distribution: (4)

Class Interval	Frequency
0-20	13
20-40	10
40-60	15
60-80	8
80-100	11

Hence, find the mode.
Answer:

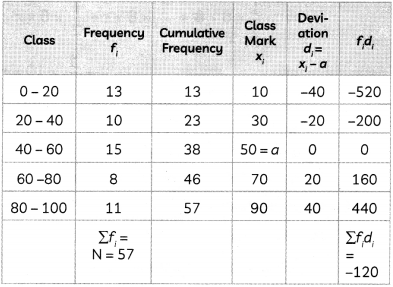
Calculation of Mean:
We know,

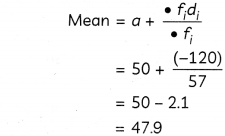
Calculation of Median:
Here, \(\frac{\mathrm{N}}{2}=28.5\)

Cumutativefrequencyjustgreaterthan 28.5 is 38, which beLongs to cLass 40 – 60.

∴ Median class 40 – 60

We know,

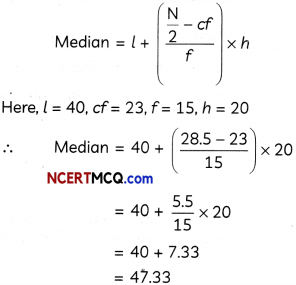
Calculation of mode:
We know,
Mode = 3 Median – 2 Mean
= 3 x 47.33 – 2 x 47.9
= 141.99-95.8
= 46.19
∴ Mean = 47.9, Median = 47.33, Mode = 46.19

Question 12.
A peacock is sitting on the top of a pillar which is 9 m high. From a point 27 m away from the bottom of the pillar, a snake is coming to its hole at the base of the pillar. Seeing the snake, the peacock pounces on it. If their speeds are equal, at what distance from the hole is the snake caught?
OR
Vanya’s mother is 28 years older than her. Seven years ago, the product of their ages, in years, was 245. Find the present age of Vanya. (4)
Answer:
Let peacock be sitting on the top P of the pillar PQ. Also, T be a point on the ground level from where snake is approaching towards the pillar. Lastly, let M be the point on the ground where the peacock caught the snake.

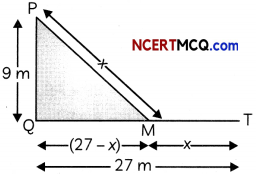
So, PQ = 9 m, QT = 27 m

Since, speed of both peacock and the snake is same, so both will cover equal distances in equaL intervals of time.
∴ Let PM = MT = x m
So, QM = (27 -x) m
So, in ΔPQM using Pythagoras theorem, we have
(PM)² = (PQ)² + (QM)²
⇒ x² = 92 +(27 -x)²
⇒ x² = 81 + 729 – 54x + x²
⇒ 54x = 810
⇒ \(\frac{810}{54}\) = 15
So, snake will caught at a distance of (27 – 15)m i.e. 12 m from the hole
OR
Let the present age of Vanya be x years.
Then, present age of Vanya’s mother = (x + 28) years
So, according to the question,
(x-7) [(x+28)-7)] = 245
⇒ (x – 7) (x + 21) = 245
⇒ x²+ 14x- 147 = 245
⇒ x² + 14x – 392 =0
⇒ x² + 28x – 14x – 392 = 0
⇒ x(x + 28) – 14(x + 28) = 0
⇒ (x – 14) (x + 28) = 0
⇒ x = 14, – 28
Since, age cannot be negative,
x = 14
Hence, the present age of Vanya is 14 years.

Question 13.
Case Study-1
The benefit of the vegetable garden, of any size, in houses, is that it can help us to stay healthy as vitamin content will be highest when we pick, vegetables right from our garden and eat them. Also, it reduces the risk of consumption of harmful chemicals which is sprayed and even injected in the vegetables to make them look fresh and healthy.

A portion of the backyard of a house has a triangular-shaped garden, on which vegetables are grown in a circular shape.

If the triangular garden ABC is right-angled at B and the sides AB, BC and AC of the garden touches the circular region with centre O at points P, Q and R. respectively with AB = 8 m and BC = 6 m, then answer the following questions.

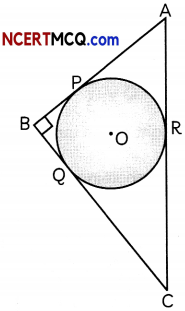
(A) If the length side AP of the garden is 5 m, find the lengths of side BQ and CR. (2)
(B) Find the radius of the circular region which is inscribed in the triangular garden. (2)
Answer:
(A) Given: AP = 5 m
Also, AB = 8 m, BC = 6 m
We know, tangents drawn from an external point to a circle are equal in length.
∴ AP = AR = 5m,
BP = BQ,
CQ = CR
Now, BQ = BP = AB – AP
= 8 – 5
= 3
and, CR = CQ = BC – BQ
= 6 – 3
= 3 m
∴ BQ = CR = 3 m

(B) Let radius of the circle be r m.

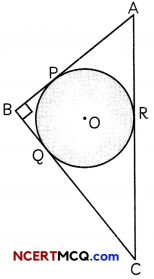
∴ OP = OQ = OR = r m
We have, AB = 8 m, BC = 6 m
Also, AC = 10 m [Applying Pythogoras theorem in ΔABC]

Now,
ar(ΔABC) = ar(ΔAOB) + ar(ΔBOC) + ar(ΔAOC)
⇒ \(\frac{1}{2}\) x BC x AB = \(\frac{1}{2}\) x AB x OP + \(\frac{1}{2}\) x BC x OQ+ \(\frac{1}{2}\) x AC x OR
⇒\(\frac{1}{2}\) x 6 x 8 = \(\frac{1}{2}\) x 8 x r + \(\frac{1}{2}\) x 6 x r + \(\frac{1}{2}\) x 10 xr
⇒ 24 = 4r+ 3r+ Sr
⇒ 24 = 12r
⇒ r = 2m
Hence, radius of the cirde is 2 m.

Question 14.
Case Study-2
A bird bath is a small shallow pond, or fountain, created like a basin in which birds may drink, bathe and cool themselves.

One day, Aniket, a student of class IV, saw some birds drinking water from potholes. He feels sad for them and asked his elder brother, Anshumann, who is in class X, to make a bird-bath. His brother bought some material from their store and prepare a bird bath in the shape of a cylinder with a hemispherical depression at one end as shown in the figure.

If the height of cylinderical part of bird-bath of 1.4 m and diameter of base is 70 cm, then answer the following questions:

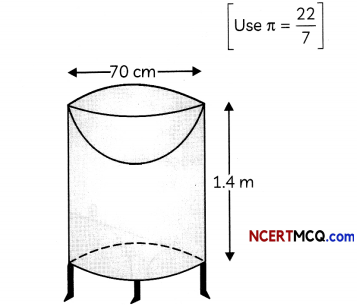
(A) Find the total surface area of the bird-bath. (2)
(B) Find the ratio of the volumes of cylindrical part and the hemispherical parts of the bird bath. (2)
Answer:
We have,
Radius of hemisphere = Radius of cylinder = \(\frac{70}{2}\) = 35 cm
and, Height of cylinder = 1.4 m
= 140 cm
∴ TSA of bird bath = CSA of cylindrical part + Area of base of cylinder + CSA of hemispherical part
= 2πrh + πr² + 2πr²
= πr(2h + r + 2r)
= πr(2h + 3r)
= \(\frac{22}{7}\) x 35(2 x 140 + 3 x 35)
= 22 x 5(280 + 105)
= 110 x 385
= 42350 cm²

Volume of cylindrical part = πr²h
Volume of hemispherical part = \(\frac{2}{3}\) ≠ r³
∴ Required ratio = \(\frac{\neq r^{2} h}{\frac{2}{3} \neq r^{3}}=\frac{3 h}{2 r}\)
= \(\frac{3 \times 140}{2 \times 35}=\frac{6}{1}\)
Hence, the ratio of volumes of cylindrical and hemispherical parts is 6:1.