CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 4 with Solutions

Students can access the Online Education CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 4 will help students in understanding the difficulty level of the exam.

Online Education CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 4 for Practice

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.
2. All questions are compulsory.
3. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
5. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study-based questions.

SECTION – A
(12 Marks)

Question 1.
Three cubes of a metal whose edges are in the ratio 3 : 4 : 5, are melted and converted into a single cube whose diagonal is 12\(\sqrt{3}\) cm. Find the edges of the three cubes.
OR
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the cylinder is 1628 sq. cm, find the volume of the cylinder. (2)
Answer:
Given: Ratio of edges of three cubes = 3 : 4 : 5
∴ Let the three edges be 3x, 4x and 5x respectively.

Also,
Diagonal of bigger cube = 12\(\sqrt{3}\)cm
∴ Edge of bigger cube = \(\frac{12 \sqrt{3}}{\sqrt{3}}\) = 12cm
[Diagonal of a cube = \(\sqrt{3}\) x Edge of the cube]

Now,
Volume of bigger cube = Volume of three cubes
⇒ (12)³ = (3x)³ + (4x)³ + (5x)³
⇒ 12 x 12 x 12 = 27x³ + 64x³ + 125x³
⇒ 12 x 12 x 12 = 216x³
⇒ x³ = \(\frac{12 \times 12 \times 12}{216}\) = 2 x 2 x 2
⇒ x = 2
∴ Edges of three cubes are 3x, 4x and 5x i.e. 6 cm, 8 cm and 10 cm respectively.
OR
Let r, h be the radius of base and height of solid right circular cylinder.
Then, according to the question r + h = 37 cm
and TSA of cylinder = 1628 cm²
⇒ 2πr(h + r) = 1628
⇒ 2 x \(\frac{22}{7}\) x r x 37 = 1628
⇒ r = \(r=\frac{1628 \times 7}{2 \times 22 \times 37}=7\) = 7
So, h = 37 – r
= 37 – 7
= 30 cm

∴ Volume of cylinder = πr²h
= \(\frac{22}{7}\) x (7)² x 30
= 4620 cm³

Question 2.
Mr. Rawat, HR manager of XYZ company, prepared a report on the number of leaves taken by its employees during the year 2020-21.

Number of leaves	Number of employees
0-10	7
10-20	13
20-30	10
30-40	12
40-50	8
50-60	11

Find the frequency of the class, succeeding the modal class of the above distribution. (2)
Answer:
We know, class with maximum frequency is called modal class.
Here, class with maximum frequency i.e. 13 is 10 – 20
∴ Modal class = 10 – 20
So, class succeeding the modal class is 20-30. Hence, the frequency of required class 20 – 30 is 10.

Question 3.
Prove that tangents drawn at the ends of diameter of a circle are parallel to each other.
Answer:
Given: A circle with centre O and diameter AOB at which tangents PQ and MN are drawn.

To prove: PQ || MN
Proof: We know, tangent is perpendicular to radius at the point of contact.
∴ PQ ⊥ OA and MN ⊥ OB
∴ ∠OAP = 90° and ∠OBN = 90°
⇒ ∠OAP = ∠OBN
But ∠OAP and ∠OBN form a pair of alternate angles between the lines PQ and MN, which are intersected by a transversal AB.
∴ PQ || MN
Hence proved.

Question 4.
A ladder, leaning against a wall, makes an angle of 60° with it. If the length of the ladder is 15 m, find the height of the wall. (2)
Answer:
Let AB be the ladder and BC be the wall.

Hence, height of the wall is 7.5 m.

Question 5.
The average score of boys in an examination of a school is 71 and that of the girls is 73. If the average score of the school in the examination is 71.8, then find the ratio of number of girls to the number of boys, who appeared in the examination. (2)
Answer:
Let the number of boys in the school be x and the number of girls be y.
Now, average score of boys = 71
∴ Total score of boys = 71 × x
= 71x
Also, average score of girls = 73
Total score of girls =73 × y
= 73y

Now,
Average score of school
\(=\frac{\text { Tota score of school }}{\text { Total number of students in school }}\)
⇒ 71.8 = \(\frac{71 x+73 y}{x+y}\)
⇒ 71.8 (x + y) = 71x + 73y
⇒ 71.8x – 71x = 73y – 71.8y
⇒ 0.8x = 1.2y
⇒ \(\frac{y}{x}=\frac{0.8}{1.2}\)
= \(\frac{2}{3}\)

Hence, the ratio of number of girls to the number of boys is 2 : 3.

Caution
In average score of school both boys and girls will be included, as a school constitute both boys and girls.

Question 6.
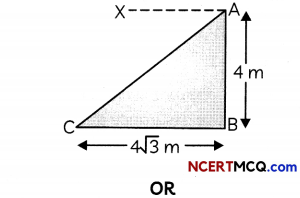
The following figure shows the observation of point C from point A. Find the angle of depression of point C from the point A.

A tower of height h m casts a shadow 90 m long and at the same time, a pole 80 m long, casts a shadow 120 m long. Find the value of h. (2)
Answer:
In ΔABC

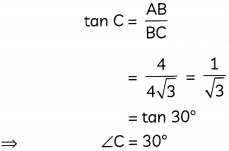
Now, angle of depression of point C from point A
= ∠XAC
= ∠ACB [Alternate angles]
30°

Caution
Here, we need to calculate ∠XAC, so calculating ∠ACB is not the final answer.
OR
Let AB be the tower and BC be its shadow. Similarly, let PQ be the pole and QR be its shadow.

Also, let angle of elevation of the Sun be θ.
∴ AB = h, BC = 90 m, PQ = 80 m, QR = 120 m and ∠C = ∠R = 0.
So, in ΔPQR

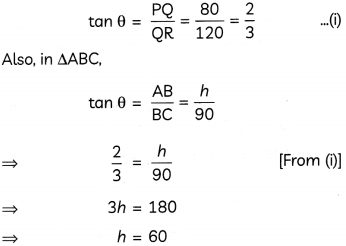
Hence, the value of h is 60.

SECTION – B
(12 Marks)

Question 7.
The sum of first seven terms of an A.P. is 63 and the sum of its next seven terms is 161. Find the tenth term of the A.P. (3)
Answer:
Let a be the first term and d be the common difference of the A.P.
We have, S₇ = 63

Solving equations (i) and (ii), we get
a = 3, d = 2
Now, 10^th term, a₁₀ = a + 9d = 3 + 9 x 2
= 21
Hence, tenth term of the A.P. is 21.

Caution
Here, 161 is the sum of next seven terms of the A.P. i.e. sum of 8^th to 14^th terms of the A.P., so apply the formula wisely.

Question 8.
Draw a line segment XY of length 5.4 cm and mark a point P on it such that PX = \(\frac{3}{5}\)XY. (3)
Answer:
We have,

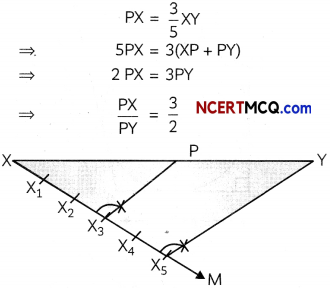
Steps of construction:

• Draw a line segment XY of length 5.4 cm.
• From point X, draw a ray XM such that ∠YXM is acute.
• On ray XM, mark 2 + 3 e. 5 points, namely X₁, X₂, X₃, X₄ and X₅ at equal distances.
• Join X₅Y.
• From point X₃, draw a line X₃P, parallel to X₅Y, intersecting XY at P.

Thus, point P divides XY in the ratio 3 : 2.

Question 9.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point R, 40 m vertically above X, the angle of elevation of the top Q of tower PQ is 45°. Find the height of the tower PQ. [Use \(\sqrt{3}\) = 1.732] (3)
Answer:
We have, RX = 40 m, ∠QRM = 45°, ∠QXP = 60°.
Here, RX = PM = 40 m and RM = XP


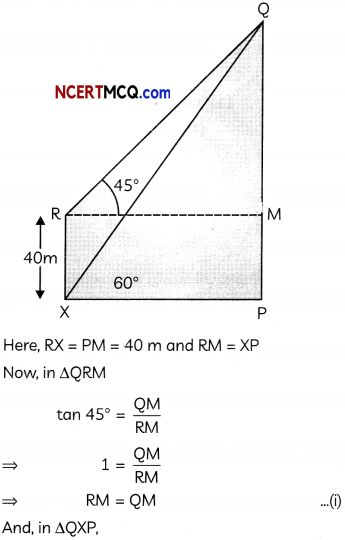
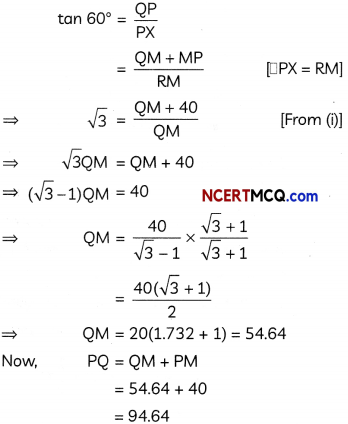
Hence, height of the tower PQ is 94.64 m.

Question 10.
Solve for x:
\(\frac{2}{x+1}+\frac{3}{2(x-2)}=\frac{23}{5 x}, x \neq 0,-1,2\)
OR
In a class test, the sum of Shrishti’s marks in maths and science is 45. If she had 1 more mark in maths and 1 less in science, the product of marks would have been 500. Find her marks in maths and science. (3)
Answer:
We have,

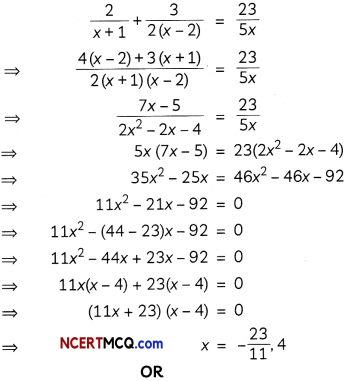
Let the Shrishti’s marks in maths be x.
Then, her marks in science = 45 – x
Now, according to the question,
(x + 1) [(45 – x) – 1] = 500
⇒ (x + l) (44 – x) = 500
⇒ 44x + 44 – x² – x = 500
⇒ x² – 43x + 456 = 0
⇒ x² – 24x – 19x + 456 = 0
⇒ x(x- 24) – 19(x- 24) = 0
⇒ (x – 19) (x – 24) = 0
x = 19, 24
if x = 19, then (45 – x) = 45 – 19 = 26
If x = 24, then (45 – x) = 45 – 24 = 21

Hence, she either got 19 marks in maths 26 marks in science or 24 marks in maths 21 marks in science.

SECTION – C
(16 Marks)

Question 11.
Rohan has a solid wax cylinder of diameter 21 cm and height 21 cm. From it, he curved out a conical cavity of maximum volume. From the remaining wax, he formed a solid sphere. Find the diameter of the sphere. (4)
Answer:
For a conical cavity of maximum volume Diameter of cavity = Diameter of cylinder
= 21 cm
and,Height of cavity = Height of cylinder
= 21 cm
∴ Radius of cavity (r) = \(\frac{21}{2}\) cm
Let the radius of the sphere be R.
Since, volume of remaining wax = Volume of cylinder – Volume of cone
And the spherical ball is formed from this remaining wax,
∴ Volume of sphere = Volume of cylinder – Volume of cone


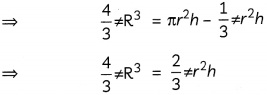
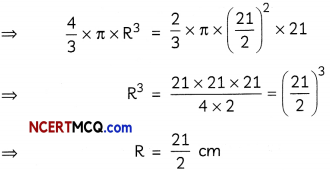
∴ Diameter of shere = 2R = 2 x \(\frac{21}{2}\) = 21cm.

Question 12
In the given figure, quadrilateral ABCD is circumscribing a circle with centre O and AD ⊥ AB. If the radius of incircle is 10 cm, then find the value of x.

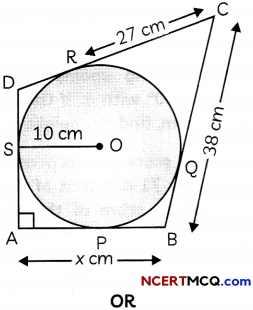
PA and PB are the two tangents to a circle with centre O in which OP is equal to diameter of the circle. Prove that ΔAPB is equilateral. (4)
Answer:
We know, tangents drawn from an external point to a circle are equal in length.

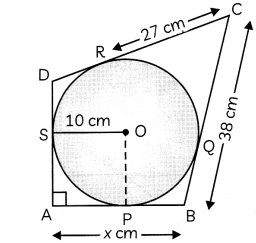
∴ AP = AS, BP = BQ,
CQ = CR and DR = DS
Now, in quadrilateral OPAS,
OS = OP = Radii, AP = AS and ∠PAS = 90°
i.e. adjacent sides are equal and an angle is a right angle.
∴ OPAS is a square.
∴ AP = AS = 10 cm
Now, CR = CQ = 27 cm
So, BP = BQ
= BC – CQ
= 38 – 27
= 11cm
So, x = AB = AP + BP
= 10 + 11
= 21
Hence, the value of x is 21.
OR
Given: A circle with centre 0 in which tangent PA and PB are drawn from an external point P.

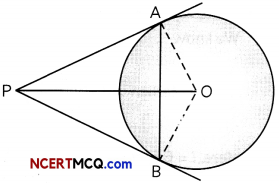
Also, OP is equal to diameter of the circle.
To prove: ΔAPB is equilateral.
Construction: Join OA and OB.
Proof: Let radius of the circle be r.
∴ OA = OB = r and OP = 2r
Now, ∠OAP = ∠OBP = 90°
[Tangent ⊥ Radius]
Let ∠OPA = 0
Then, in right angled triangle AOP
\(\sin \theta=\frac{\mathrm{OA}}{\mathrm{OP}}=\frac{r}{2 r}=\frac{1}{2}=\sin 30^{\circ}\)
⇒ θ = 30°
Since, tangents are equally inclined to the line segment joining the centre of the circle to their common external point.
∴ ∠OPA = ∠OPB = \(\frac{1}{2}\) ∠APB
or, ∠APB = 2∠OPA = 2 x 30° = 60°
We know, tangents drawn from an external point to a circle are equal in length.
∴ In ΔAPB,
PA = PB
⇒ ∠PBA = ∠PAB = x° (say)
So, \(x^{\circ}=\frac{180^{\circ}-\angle \mathrm{APB}}{2}=\frac{180^{\circ}-60^{\circ}}{2}\)
= 60°
i.e. ∠PBA = ∠PAB = ∠APB = 60°
∴ ΔAPB is an equilateral triangle.

Hence, proved.

Question 13.
Case Study-1
A loan is an amount which one receives from a bank with the assurance of returning it in the future along with some fixed annual interest.

Deepak took a loan of ₹ 1,18,000 from HDFC bank to invest in his start-up. He has to repay this loan by paying every month, starting with the first installment of ₹ 1000. Since, his start-up was going well, he decided to increase the installment of loan by ₹ 100 every month.

Based on this information answer the following question.
(A) What amount of ban he still have to pay after the 30th installment? (2)
(B) What amount will be paid to the bank as the last installment of ban? (2)
Answer:
(A) Since installments paid by Deepak, each successive month, increases uniformly by a fixed amount, so his series of installments form an A.P. with a = 1000 and d = 100.
∴ Amount paid till 30 installments
= S₃₀
= \(\frac{30}{2}\) [2 x 1000 + (30 – 1) x 100]
∵ [S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
= 15 x 4900
= 73500

So, amountto be pay after 30th installment = Total amount to be paid – A amount paid till 30 installments = ₹ (1,18,000-73,500)
= ₹ 44,500

(B) Let the loan of ₹ 1,18,000 be repaid to the bank in n months.
Then, S_n = 118000
⇒ \(\frac{n}{2}\) [2a + (n – 1)d]
= 118000
⇒ \(\frac{n}{2}\) [2 x 1000 + (n – 1) x 100] = 118000
⇒ \(\frac{n}{2}\) [1900+ 100n] = 118000
⇒ n(950 + 50n) = 118000
⇒ 50n² + 950n – 2360 = 0
or n² + 19n – 2360 = 0
⇒ (n + 59) (n – 40) = 0
⇒ n = -59, 40
Since, number of months cannot be negative
∴ n = 40
Amount paid in last installment = a₄₀
= a + 39d
= 1000 + 39 x 100
= 4900
Hence, the amount paid in the last installment of the loan is ₹ 4900.

Question 14.
Case Study-2
‘Swachh Bharat Abhiyan’ is a country-wide campaign initiated by our Honourable Prime Minister of India, Mr. Narendra Singh Modi in the year 2014 to eliminate open defecation, to improve solid waste management and to accelerate the efforts to achieve universal sanitisation.

As part of the ‘Swachh Bharat Abhiyan’, some houses of a locality in Agra decided to clean up and beautify a Primary School of their locality by planting a number of plants. They involved the school kids and the local community in doing so.

Here is the data indicating the number of plants contributed by different houses:

Number of plants contributed	Number of houses
1-3	10
4-6	8
7-9	X
10-12	7
13-15	12
16-18	4

(A) If the mean number of plants contributed be 8.9, then how many houses contributed 7 to 9 plants? (2)
(B) Find the median number of plants contributed. (2)
Answer:

Hence, 9 houses contributed 7 to 9 plants.

(B)

Class	Frequency	Cumulative Frequency
0.5 – 3.5	10	10
3.5 – 6.5	8	18
6.5 – 9.5	X = 9	27
9.5 – 12.5	7	34
12.5 -15.5	12	46
15.5 -18.5	4	50
	N = 50

Here, \(\frac{N}{2}=25\)
Cumulative frequency just greater than 25 is 27 which belongs to class 6.5 – 9.5.
∴ Median class = 6.5 – 9.5.