CBSE Sample Papers for Class 11 Applied Mathematics Term 2 Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Term 2 Set 1 with Solutions

Time : 2 Hours
Maximum Marks : 40

General Instructions:

• The question paper is divided into 3 sections -A, B and C.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study-based question. Internal choice has been provided in one question.

Section – A [2 Marks each]

Question 1.
A particle moves along the curve x² = 2y. At what point, ordinate increases at the same rate as abscissa increases?
OR
A stone is dropped into a quiet lake and waves move in a circle at a speed of 3.5 cm/sec. At the instant when the radius of the circular wave is 7.5 cm, how fast is the enclosed area increasing?
Answer:
Given curve, x² = 2y …(i)
Differentiating both sides w.r.t. t, we get
2x\(\frac{d x}{d t}\)= 2\(\frac{d y}{d t}\)
⇒ 2x\(\frac{d x}{d t}\)= 2\(\frac{d y}{d t}\) (∵ Given, \(\frac{d y}{d t}=\frac{d x}{d t}\))
⇒ x = 1
From eq. (i), y = \(\frac{1}{2}\)
So, the required points is (1, \(\frac{1}{2}\))

Commonly Made Error: Some students get confused between abscissa and ordinate. Some student find y but fail to find the point by suitable substitution.

Answering Tip:
Adequate practice is required in problems involving rate of change of bodies.

OR

Let r be the radius and A be the area of circular wave at any time t.

Question 2.
Mr. Raghav aged 26 years and a resident in India, has a total income of ₹4,40,000, comprising his salary
income and interest on bank fixed deposit. Compute his tax liability for A.Y. 2020-21.
Answer:
Computation of tax liability of Mr. Raghav for A.Y. 2020-21

Particulars	₹
Tax on total income of ₹ 4,40,000
Tax @5% of ₹ 1,90,000 (₹ 4,40,000 – ₹ 2,50,000)	9,500
Less: Rebate u/s 87A (Since total income ≤ ₹ 5,00,000)	9,500
Tax Liability	Nil

Question 3.
A machine can be purchased for ₹50,000. Machine will contribute ₹12,000 per year for the next five years.
Assume borrowing is 10% per annum compounded annually. Determine whether machine should be purchased or not. Given P (5,0.10) = 3.79079.
OR
₹5000 is paid every year for three years to pay off a loan. What is the loan amount if interest rate be 14% per annum compounded annually?
Answer:
The present value of annual contribution
P.V. = C.F. × P(n, i)
Here, C.F. = ₹ 12,000, i = 10% = \(\frac{10}{100}\) = 0.10
n = 5
and P(5,0.10) = 3.79079
∴ P.V = 12000 × 3.79079
= ₹ 45489.48 %
which is less than the initial cost of the machine. Therefore, machine must not be purchased.
OR

Therefore, PV. = C.F. P{n, i)
= 5000 × 2.3216
= ₹ 11,608

Question 4.
Three identical dice are rolled. Find the probability that the same number appears on each of them.
Answer:
Since, three identical dice are rolled, so number of elements in the sample space S is
n(S) = 6³ = 216 y2
Let E be the event of getting same number on each of them i.e., E = {(1,1,1), (2,2,2), (3,3,3), (4,4,4), (5, 5,5), (6, 6,6)}
⇒ n(E) = 6
∴ P(E) = \(\frac{n(E)}{n(S)}=\frac{6}{216}=\frac{1}{36}\) Hence, the probability that the same number appears on all the three dice is \(\frac{1}{36}\).

Question 5.
Find the condition, if the two lines ax + by = c and a’x + b’y = a’b’ are perpendicular.
Answer:
The given lines are:
ax + by = c

⇒ aa’ + bb’ = 0, which is the required condition

Question 6.
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.
Answer:
The number of ways of selecting 3 red balls out of 6 red balls = ⁶C₂
The number of ways of selecting 3 white balls out of 5 white balls = ⁵C₃
The number of ways of selecting 3 blue balls out of 5 blue balls = ⁵C₃
The number of ways of selecting 3 balls of each colour = \({ }^{6} C_{3} \times{ }^{5} C_{3} \times{ }^{5} C_{3}\)
= \({ }^{6} C_{3} \times{ }^{5} C_{3} \times{ }^{5} C_{3}\)
[Using property ⁿC_r = ⁿC_r-1
= \(\frac{6 \times 5 \times 4}{1 \times 2 \times 3} \times \frac{5 \times 4}{1 \times 2} \times \frac{5 \times 4}{1 \times 2}\)
= 20 × 10 × 10
= 2000

Section – B (4 marks each)

Question 7.
In a college, 70% students pass in Physics, 75% pass in Mathematics and 10% students fail in both. One student is chosen at random. What is the probability that:
(i) he passes in Physics given that he passes in Mathematics?
(ii) he passes in Mathematics given that he passes in Physics?
Answer:
Let x% students passes in both Mathematics and Physics.

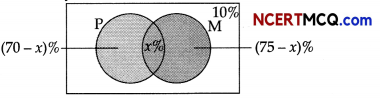
Students who pass in Physics = 70%
∴ P(Ph) = \(\frac{70}{100}\)
Students who pass in Mathematics = 75%
∴ P(M) = \(\frac{75}{100}\)
Students who fail in both = 70%
Now, 70% – x + x + 75% – x = 90%
⇒ x = 55%
∴ P(M ∩ Ph) = \(\frac{55}{100}\)

(i) Probability that student passes in Physics given that he passes in Mathematics is

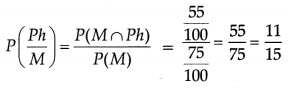
(ii) Probability that student passes in Mathematics given that he passes in Physics is

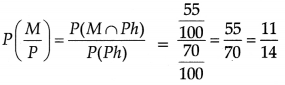
Question 8.
(i) Find the shortest distance of the point (8,1) from the circle (x + 2)² + (y – 1)² = 25.
(ii) Find the farthest distance of the point (1, 5) from the circle (x – 1)² + (y + 1)² = 16.
OR
Prove that the equation of parabola, whose vertex and focus are on the axis of X at distances a and a’ from the origin respectively, is y² = 4a(a’ – a) (x – a).
Answer:
(i) The centre of the circle (x + 2)² + (y – 1)² = 25 is C(- 2, 1) and its radius (r) is 5.

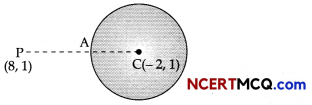
If P is the point (8,1), then
CP = |\(\sqrt{(8+2)^{2}+(1-1)^{2}}\)|
= 10 units
The shortest distance of P from the circle
= PA
= CP – AC
= 10 – 5
= 5 units

(ii) The centre of the circle (x – 1)² + (y + 1)² = 16 is C(1, – 1) and its radius (r) = 4.

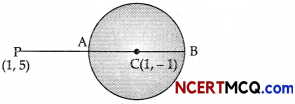
If P is the point (1, 5), then
CP = \(\sqrt{(1-1)^{2}+(5+1)^{2}}\)
= 6
The farthest distance of point P(1, 5) from the circle = PB
= CP + BC
= 6 + 4
= 10 units

OR

Let A be the vertex and S be the focus of the required parabola and these lie on the X-axis. Since, distances of A and S from the origin are a and a’, respectively.
So, the coordinates of A are (a, 0) and coordinates of S are (a’, 0).

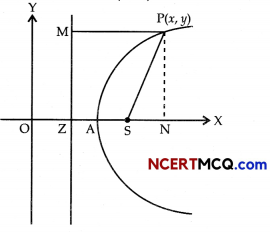
Therefore, AS = a’ -a = AZ
Also, ZM is the directrix of the parabola.
∴ OZ = OA – AZ
= a – (a’ – a) = 2a – a’
Now, consider any point P(x, y) on the parabola and draw PM perpendicular from P on the directrix and PN perpendicular on the X-axis, from figure, it is clear that
PM = NZ
= ON – OZ
= x – (2a – a’)
= x – 2a + a’
Therefore, by definition of parabola, we have
SP = PM
⇒ \(\sqrt{\left(x-a^{\prime}\right)^{2}+(y-0)^{2}}\) = x – 2a + a’
⇒ (x – a’)² + y² = (x – 2a + a’)²
⇒ y² = (x – 2a + a’)² – (x – a’)²
⇒ y² = [(x – 2a + a’) – (x – a’)]
[(x – 2a + a’) + (x – a’)]
⇒ y² = (2a’ – 2a) (2x – 2a)
⇒ y² = 4(a – a’)(x – a)
Hence Proved.

Question 9.
In an automobile factory, certain parts are to be fixed into the chassis in a section before it moves into another section. On a given day, one of the three people A, B and C carries out this task. A has 45% chance, B has 35% chance and C has 20% chance of doing the task. The probability that A, B and C will take more than the allotted time is \(\frac{1}{6}\), \(\frac{1}{10}\) and \(\frac{1}{20}\), respectively. If it is found that the time taken is more than the allotted time, what is the probability that A has done the task?
Answer:
Let E₁ E₂ and E₃ denote the events of carrying out the task A, B and C, respectively.
Let H denote the event of taking more time. Then, P(E₁) = 0.45, P(E₂) = 0.35 and P(E₃) = 0.20
Also,

Commonly Made Error:
Many students used Bayes’ Theorem correctly but took the probabilities of A, B, C as 45,35, and 20, instead of percentages. Some candidates did not implement the theorem correctly.

Answering Tip:
Be clear that probabilities are ratios and not numbers. Learn conditional probability concept which helps the student to understand the advance concept of Bayes’ Theorem.

Question 10.
The difference between simple and compound interests compounded annually on a certain sum of money for 2 years at 4% per annum is ₹1. Find the sum.
Answer:
Let the sum be ₹x. Then,
Compound Interest = A_n – P
⇒ I = P(1 + i)ⁿ – P
Here, P = x, i = 4% = \(\frac{4}{100}\) = 0.04, n =2
Compound Interest = x(1 + 0.04)² – x
= \(\frac{676}{625}\)x – x
= \(\frac{51 x}{625}\)
Now, simple interest,
I =Pit
= x × 0.04 × 2
= \(\frac{2 x}{25}\)
Since, given difference = ₹ 1
i.e., \(\frac{51 x}{625}-\frac{2 x}{25}\) = 1
⇒ x = 625

Section – C [4 Marks each]

Question 11.
How many words, with or without meaning can be made from the letters of the word ‘MONDAY’, assuming that no letter is repeated, if
(i) 4 letters are used at a time.
Answer:
In the word MONDAY, all letters are different.
(i) Out of 6 different letters, 4 letters can be selected in ⁶C₄ ways.
∴ Required number of words
= ⁶C₄ × 4! = ⁶P₄
= \(\frac{6 !}{(6-4) !}\) = \(\frac{6 !}{2 !}\) = \(\frac{6 \times 5 \times 4 \times 3 \times 2 !}{2 !}\) = 360

(ii) all letters are used at a time.
Answer:
The word ‘MONDAY’ has 6 different letters.
Number of ways taking 6 letters at a time = ⁶P₆
∴ Required number of words = ⁶P₆
= \(\frac{6 !}{(6-6) !}\) = \(\frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{0 !}\) = 720

(iii) all letters are used but first letter is a vowel.
Answer:
First, we will fix the vowel.
In the word MONDAY, there are two vowels O and A.
∴ First letter can be chosen by 2 ways.
Number of ways taking 5 different letters from remaining 5 letters = ⁵P₅
∴ Required number of words
= ⁵P₅ = \(\frac{5 !}{(5-5) !}\) = \(\frac{5 !}{0 !}\)
= 5 × 4 × 3 × 2 × 1 = 120
Hence, total number of ways = 2 × 120 = 240

Question 12.
Manjeet, Dilawar and Ravi live in the same city. Manjeet sells an article to Dilawar for ?60,000 and Dilawar sells the same article to Ravi at a profit of ₹8,000. If all the transactions are under GST system at the rate of 12%, find:
(i) The state-government tax (SGST) paid by Dilawar.
(ii) The total tax received by CGST.
(iii) How much does Ravi pay for the article?
OR
OR
X, who is a person with disability, submits the following information.

Particulars	Amount (₹)
(i) Salary (per annum)	3,05,000
(ii) Rent received (per month)	2,000
(iii) Dividend From Co-operative Society	3,000
(iv) Interest on Bank Deposits	7,000
(v) Interest on Government securities	5,000
(vi) Winnings from Lotteries	2,000
(vii) NSC (VIII Issue) purchased during the year	15,000
(viii) Deposit under PPF Scheme	35,000

He earned a long-term capital gain of ₹78,000 on sale of shares during the year. Compute
(a) the taxable income; (b) the tax payable for the assessment year 2020-21.
Answer:
Given the rate of GST = 12%
∴ CGST rate = SGST rate = 6%

(i) Tax paid by Dilawar to SGST = SGST received by Dilawar on selling price – SGST paid by him on purchasing
= \(\frac{6}{100}\) × (60,000 + 8,000) – \(\frac{6}{100}\) x 60,000 % 100 100
= \(\frac{6}{100}\) × 68,000 – \(\frac{6}{100}\) x 60,000
= \(\frac{6}{100}\) × (68,000 – 60,000)
= \(\frac{6}{100}\) × 8,000
= ₹ 480

(ii) Total tax received by CGST = CGST paid by Manjeet + CGST paid by Dilawar Vi
= \(\frac{6}{100}\) × 60,000 + ₹480 100
= ₹(3600 + 480)
= ₹4080

(iii) The amount, Ravi paid for the article
= Cost price of the article for Ravi with GST
= ₹ \(\left(68000+\frac{12}{100} \times 68000\right)\)
= ₹ (68000 + 8160)
= ₹ 76160

OR

(a) Computation of Total Income

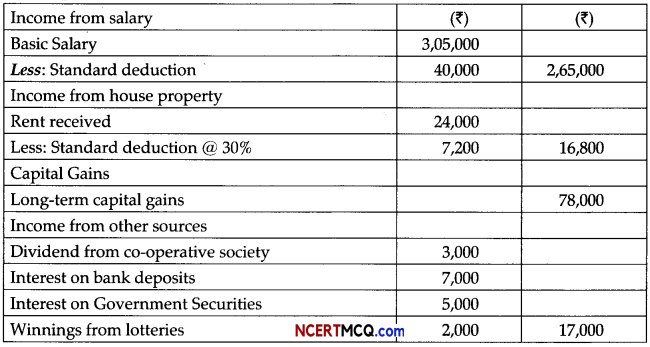
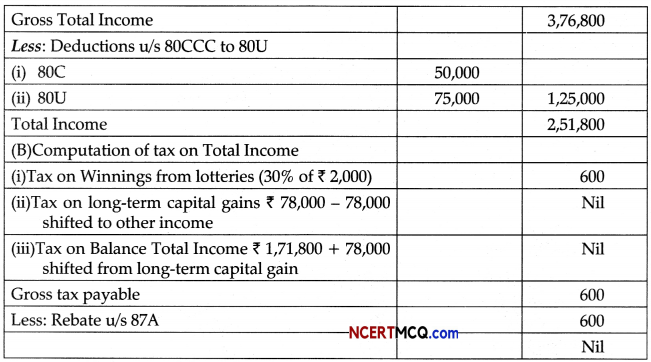
Note: Income from winning of lotteries cannot be shifted to other income to claim full exemption of ₹ 2,50,000.

Question 13.
An air force plane is ascending vertically at the rate of 100 km/hr. If the radius of the earth is r km, how fast the area of the earth, visible from the plane, increasing at 3 minutes after it started ascending? Given that the visible area A at height h is given by A = 2πr²\(\frac{h}{r+h}\).
Answer:
It is given that the plane is ascending vertically at constant rate of 100 km/hr.
∴ \(\frac{d h}{d t}\) = 100 km/hr.
⇒ Height of the plane after 3 minutes = 100 × \(\frac{3}{60}\) = 5 km [Using h = vt]

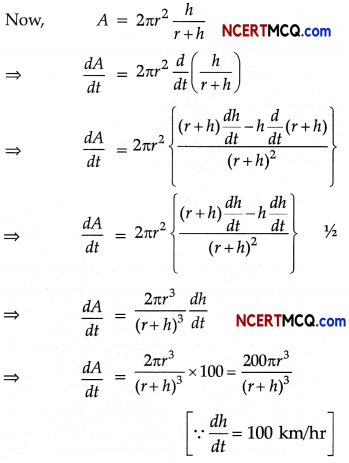
We have to find when t = 3 minutes and at t = 3, we have h = 5 km.
∴ At t = 3,
\(\frac{d A}{d t}=\frac{200 \pi r^{3}}{(r+5)^{2}}\)

Question 14.
Dakshin Haryana Bijli Vitran Nigam, also known as DHBVN is an Indian state-owned power distribution utility company. It is owned by Government of Haryana and its headquarter is located in Hisar city of Haryana. It is responsible for distribution of power in 12 districts of Haryana.

Recently, it revised the tariff rates of electricity for both the industrial and domestic units as follows:
For industrial units:

Unit slab	Rate per unit (in ₹)	Fixed Charge (in ₹)
1-300	7.50	330
301-500	8.40	390
501 and above	8.75	450

For domestic units:

Unit slab	Rate per unit (in ₹)	Fixed Charge (in ₹)
1-150	5.50	110
151-300	6.00	125
301-500	6.50	187
501 and above	7.00	221

Electricity duty will be 5% (for both industrial and domestic units).
Based on the information given above, solve the following problems:
(a) Sumit owns a shoe factory and the monthly consumption of electricity units are 550, calculate the electricity bill. (2)
Answer:

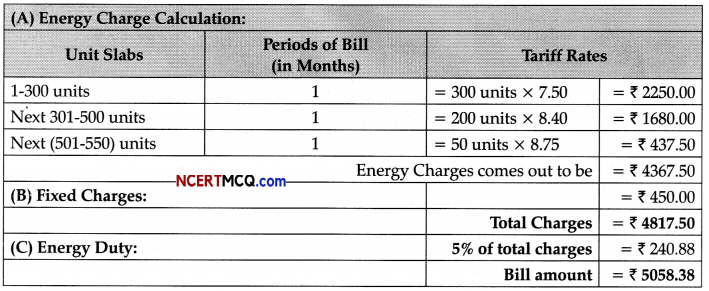
Thus, final bill amount is ₹ 5058.38.

(b) Ranjana is a housewife and her monthly consumption of electricity units are 275, calculate the electricity bill. (2)
Answer:

Thus, final bill amount is ₹ 1785.