CBSE Sample Papers for Class 11 Applied Mathematics Term 2 Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Term 2 Set 2 with Solutions

Time : 2 Hours
Maximum Marks : 40

General Instructions:

• The question paper is divided into 3 sections -A, B and C.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study-based question. Internal choice has been provided in one question.

Section – A [2 Marks each]

Question 1.
Evaluate

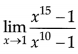
OR
Differentiate 3^x + x³ + 4x – 5 with respect to x.
Answer:

OR
Let, f(x) = 3^x + x³ + 4x – 5
f'(x) = \(\)f(x)
f’(x) = \(\)(3^x + x³ + 4x – 5)
= 3^x in 3 + 3² + 4 × 1
= 3^xln 3 + 3x² + 4

Question 2.
Five 100 W bulbs are used for 10 hours every day for 30 days. Find the cost of electricity if the rate is ₹ 4.00 per unit.
Answer:
Five bulbs consume the power of 100 W each.
The total power consumed by 5 bulbs = 5 × 100
= 500 W = 0.5 kilowatt
(∵ lkW = 1000 W)

Electrical energy consumed daily is,
E = P × t = 0.5 kW × 10 hours 14 = 5 kWh.

Thus, total electrical energy consumed for 30 days
= 5 kWh × 30 days = 150 kWh or 150 units.

The cost of 1 unit of electricity
= ₹ 4

Thus, the total cost of electricity = ₹ 4 × 150 = ₹ 600

Question 3.
Mr. Roy need to borrow money. His neighbourhood bank charges 8% interest compounded semi-annually. An internet bank charges 7.9% interest compounded monthly. At which bank will Mr. Roy pay lesser amount of interest?
OR
ABC Ltd. wants to lease out an asset costing ₹ 36,000 for five years has fixed rental of ₹ 1,05,000 per annum payable annually starting from the end of first year. Suppose rate of interest is 14% per annum compounded annually on which money can be invested by the company. Is this agreement favourable to the company ?
Answer:
Compare effective rates : Neighbourhood bank,
E = (1 + \(\frac{0.08}{2}\))² – 1
= 0.0816 ≈ 8.16%

Internet bank,
E = (1 + \(\frac{0.79}{12}\))² – 1 = 0.08192 ≈ 8.19%
The neighbourhood bank has the lower effective rate although it has a higher nominal (actual) rate.
OR
First we have compute the present value of the annuity of ₹ 1,05,000 for five years at the interest rate of 14% p.a. compounded annually.
The present value PL of the annuity is given by = C.F. × P(n, i)
Here, C.F. = 1,05,000, i = 14% = 0.14, n = 5 and P(n, i) = P(5, 0.14) = 3.43308
∴ P.V. = 1,05,000 × 3.43308
= ₹ 360473.40
which is greater than the initial cost (₹ 3,60,000) of the asset and consequently leasing is favourable to the lessor.

Question 4.
A couple has 2 children. Find the probability that both are boys, if it is known that (i) one of them is boy (ii) the older child is a boy.
Answer:
Sample space = {B₁, B₂, B₁ G₂, G₁ B₂, G₁ G₂} where, B₁ and G₁ are the older boy and girl, respectively.

Let E₁ = both the children are boys
E₂ = one of the children is a boy
E₃ = the older child is a boy

(i) P(one of them is a boy) = P\(\left(\frac{E_{1}}{E_{2}}\right)\)
= \(\frac{P\left(E_{1} \cap E_{2}\right)}{P\left(E_{2}\right)}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}\)

(ii) P(older child is a boy) = P\(\left(\frac{E_{1}}{E_{3}}\right)\)
= \(\frac{P\left(E_{1} \cap E_{3}\right)}{P\left(E_{3}\right)}=\frac{\frac{1}{4}}{\frac{2}{4}}=\frac{1}{2}\)

Commonly Made Error:
Students get confused while finding (E₁ ∩ E₂) and (E₁ ∩ E₃). Errors are also made in using conditional probability formulae.

Answering Tip
Independent cases or mutually exdusive situations need plenty of illustration. Conditional probability problems need to be practice thoroughly.

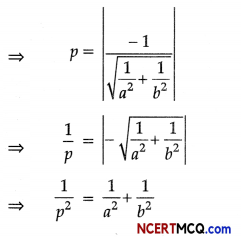
Question 5.
If ’p’ is the length of the perpendicular from the origin to the given line whose intercepts on axes are ‘a’ and ‘b’, then find the relation between a, b and p.
Answer:
Equation of the line which makes intercepts ‘a’ and ‘b’ on the axes is
\(\frac{x}{a}+\frac{y}{b}\) = 1

∴ The perpendicular distance ‘p’ from the origin is

Question 6.
In how many ways can the letter of the word “PENCIL” be arranged so that I is always next to L.
Answer:
There are 6 letters in the word “PENCIL”. Consider LI as one letter. Now, 5 letters (P E, N, C,… LI) can be arranged in ⁵P₅ = 5! = 120 ways.
Hence, the total number of ways in which I is always next to L is 120.

Commonly Made Error:
Sometimes students take permutation of 5 letters arrangement as ⁶P₅ instead of ⁵P₅. which leads to incorrect result.

Answering Tip:
Read the question carefully and then decide whether to take ⁶P₅ on ⁵P₅.

Section – B [3 Marks each]

Question 7.
A young man visits a hospital for medical check up. The probability that he has lungs problem is 0.55, heart problem is 0.29 and either lungs or heart problem is 0.57. What is the probability that he has
(i) both type of problems: lungs as well as heart ?
(ii) lungs problem but not heart problem ?
(iii) Out of 1000 persons, how many are expected to have both type of problems ?
Answer:
Let ‘L’ and ‘H be the events that the young man has lungs problem and heart problem respectively.
∴ P(L) = 0.55, P(H) = 0.29, P(L ∪ H) = 0.57 P(E ∩ H) = ?
(i) We know that,
⇒ P(E ∪ H) = P(L) + P(H) – P(L ∩ H)
⇒ P(L ∩ H) = P(L) + P(H) – P(E ∪ H)
⇒ 0.55 + 0.29 – 0.57
= 0.27
∴ The probability that he has both the problems is 0.27.

(ii) P(E ∩ H) = P(E) – P(E ∩H)
= 0.55 – 0.27 = 0.28 1
∴ The probability that he has lungs problem but not heart problem is 0.28.

(iii) Out of 1000 persons, the number of
persons having both the problems = 0.27 × 1000 = 270.

Question 8.
If two diameters of a circle lie along the lines x – y – 9 = 0 and x – 2y – 7 = 0 and the area of the circle is 38.5 sq. units, find the equation.
OR
A double ordinate of parabola y² = 4ax is of length 8a. Prove that the lines from the vertex to its ends are at right angles.
Answer:
Given, two diameters of a circle lie along the lines
x – y – 9 = 0 …(i)
and x – 2y – 7 = 0 …(ii)
So, their point of intersection is the centre of the circle.
Solving eqs. (i) and (ii), simultaneously, we get
x = 11 and y = 2
∴ The centre of the circle is (11, 2).
Let r be the radius of the circle, then
Area = πr² = 38.5 sq units (given)

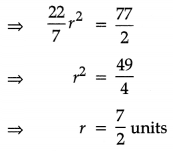
∴ The equation of the circle is
(x – 11)² + (y – 2)² = (\(\frac{7}{2}\))²
x² + y² – 22x – 4y + 125 = \(\frac{49}{4}\)
= x² + y² – 22x – 4y + 125 – \(\frac{49}{4}\) = 0
= 4(x² + y²) – 88x – 16y + 451 = 0
is the required equation of circle.

OR

Let PQ be the double ordinate of length 8a of the parabola y² = 4ax. Then, PR = QR = 4a.
Let AR = x₁ then coordinates of point P are (x₁ 4a) and coordinates of point R are (x₁ – 4a).

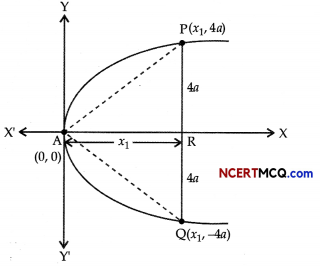
Since, P lies on y² = 4ax
(4a)² = 4ax₁
⇒ x₁ = 4a

So, coordinates of P and Q are (4a, 4a) and (4a, – 4a), respectively.
Also, the coordinates of the vertex A are (0, 0)
∴ m₁ = slope of AP = \(\frac{4 a-0}{4 a-0}\) = 1
and m₂ = slope of AQ = \(\frac{-4 a-0}{4 a-0}\) = -1
Clearly, m₁m₂ = -1
Hence, AP ⊥ AQ.
Thus, the lines from the vertex of its ends are at right angles.
Hence Proved.

Question 9.
In a single throw of two dice, determine the probability of getting a total of 7 or 9.
Answer:
Let S be the sample space. Then, n(S) = 6² = 36
Let ‘A’ and ‘B’ be the events of getting a total of 7 and 9 respectively.
∴ A = {(1,6), (2, 5), (3,4), (4, 3), (5,2), (6,1)}
n(A) = 6
B = {(3,6), (4,5), (5,4), (6, 3)} A ∩ (B) = 4
A ∩ B = Φ ⇒ n(A ∩ B) = 0 n(A) 4
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{4}{36}\)
P(B) = \(\frac{n(B)}{n(S)}=\frac{4}{36}\)

and P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}\) = 0

We know that,
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{36}+\frac{4}{36}\) – 0
= \(\frac{10}{36}=\frac{5}{18}\)
∴ The probability of getting a total of 7 or 9 is \(\frac{5}{18}\)

Question 10.
A machine with useful life of seven years costs ₹ 10,000 while another machine with useful life of five years costs ₹ 8,000. The first machine saves labour expenses of ₹ 1,900 annually and the second one saves labour expenses of ₹ 2,200 annually. Determine preferred course of action. Assume cost of borrowing as 10% compounded per annum.
[Given, P(7,0.10) = 4.86842, P(5,0.10) = 3.79079]
Answer:
The present value of annual cost saving for the first machine = C.F. × P(n, i)
Here, C.F. = ₹ 1900, P(n, i) = P(7, 0.10) = 4.86842
n = 7 and i = 10% = \(\frac{10}{100}\) = 0.10
∴ Present value = 1900 × P(7, 0.10)
= 1900 × 4.86842 A
= 9249.99 = ₹ 9250
Cost of machine being ₹ 10,000, it costs more by ₹ 750 than it saves in terms of labour cost. A The present value of annual cost saving of second machine
= C.F. × P(n, i)
= 2000 × P(5, 0.10)
= 2000 × 3.79079 = ₹ 8339.74
Cost of the second machine being ₹ 8000, effective saving in labour cost is ₹ 339.74. Hence, the second machine is preferable.

Section – C [4 Marks each]

Question 11.
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if a team has :
(a) no girl
(b) at least 3 girls
Answer:
(i) no girl

(ii) at least 3 girls?
Since, the team has to consist of at least 3 girls, the team can consist of
(a) 3 girls and 2 boys
(b) 4 girls and 1 boy

(a) 3 girls and 2 boys

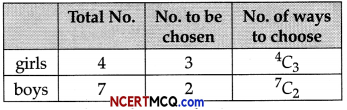
Number of ways selecting = ⁷C₂ × ⁴C₃
= \(\frac{7 !}{2 ! 5 !} \times \frac{4 !}{3 ! 1 !}\)
= \(\frac{7 \times 6}{2 \times 1}\) × 4
= 84

(b) 4 girls and 1 boy

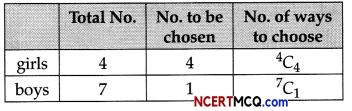
Number of ways selecting = ⁷C₂ × ⁴C₃
= \(\frac{7 !}{1 ! 6 !} \times \frac{4 !}{4 ! 0 !}\)
= 7 × 1
= 7

∴ Total number of ways = 84 + 7 = 91

Question 12.
From the following information, compute the tax liability of R, for the assessment year 2020-21.

	₹
Business income	4,60,000
Receipt from sale of trees of spontaneous growth	1,00,000
Agricultural income	60,000

OR
For a non-domestic connection monthly consumption of water is 150 kilolitres, then find the water bill for a month. Tariff rates can be considered as the table given below:

Monthly Consumption (in Kilolitre)	Service Charge (in ₹)	Volumetric Charge (Per kl in ₹)
0-06	146.41	17.57
06-15	292.82	26.35
15-25	585.64	35.14
25-50	1024.87	87.85
50-100	1171.28	140.56
>100	1317.69	175.69
Plus Sewer Maintenance Charge: 60% of water volumetric charge

Answer:
Computation of tax liability of R

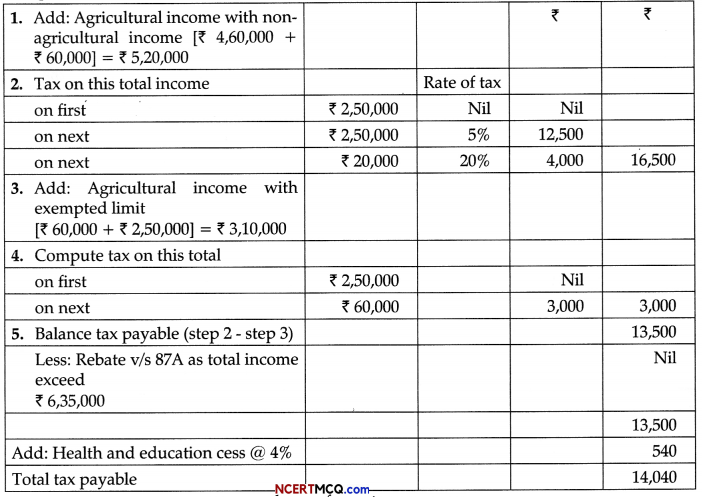
Note: Receipt from sale of trees which are of spontaneous growth is a capital receipt and not taxable under the head capital gain as trees of spontaneous growth can be said to be self generated and their cost of acquisition cannot be determined.

OR
Volumetric Charge for consumption upto 6 kl = ₹ 6 × 17.57 = ₹ 105.42
Volumetric Charge for consumption between 6-15 kl = ₹ 9 × 26.35 = ₹ 237.15
Volumetric Charge for consumption between 15-25 kl = ₹ 10 × 35.14 = ₹ 351.4
Volumetric Charge for consumption between 25-50 kl = ₹ 25 × 87.85 = ₹ 2196.25
Volumetric Charge for consumption between 50-100 kl = ₹ 50 × 140.56 = ₹ 7028
Volumetric Charge for consumption between 100-150 kl = ₹ 50 × 175.69 = ₹ 8784.5

Total volumetric Charge for consumption of
150 kl = (105.42 + 237.15 + 351.4 + 2196.25 + 7028 + 8784.5) = ₹ 18702.72
Service Charge = ₹ 1317.65
Sewage Charges = 60% of Volumetric Charges
= 18702.72 × 60% = ₹ 11221.63
Amount of water bill for the given month =
₹ (18702.72 + 13I7.65 + 11221.63) = ₹ 31242
Thus, amount of non-domestic water bill is ₹ 31242.

Question 13.
Find the derivative of \(\frac{x+1}{x-1}\) by the first principle method.
Answer:

Question 14.
In XI standard, teacher was discussing the concept of Future Value of Annuity Regular. During his class, he discussed the following few points on this: ₹ 500 was invested in annuity (future value regular) for 10 years at the rate of 14% compounded annually.

On the basis of the above information, answer the following questions:
If C.F. be the periodic payments, (cash flow in each period), the future value F.V (n, i) of the annuity is given by:
Future value (F.V) of an Annuity = C.F\(\left[\frac{(1+i)^{n}-1}{i}\right]\)
(a) What will be the future value of annuity at the end of two years? Given that (1.14)² = 1.2996. Also,
find the future value of the annuity after 3 years. Given that (1.14)³ = 1.4815 (2)
(b) What is the approximate difference between the future value of the annuity for five years and three years? Given that (1.14)⁵ = 1.925. What is the difference between the profit earned by future value of the annuity for two years and the ₹ 1000 invested compounded for two years with the same interest rate? (2)
Answer:
(a) By using formula,
F.V. of an Annuity= C.F.\(\left[\frac{(1+i)^{n}-1}{i}\right]\)
Here, C.E = 500, i = 0.14, n = 2
By putting these values, we get:
EV. of an Annuity at the end of two years
= 500\(\left[\frac{(1+0.14)^{2}-1}{0.14}\right]\)
= \(\frac{0.2996}{0.14}\)
= 500 × 2.14
= ₹ 1070
Also, EV. of annuity at the end of three years:
After three years future value of an annuity

(b) The approximate difference between the future value of the annuity for five years and three years:
After three years future value of the annuity
= ₹ 1719.64
After five years future value of the annuity

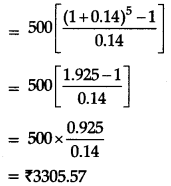
Therefore, difference
= 3305.57 – 1719.64
= ₹ 1585.93
Now, the difference between the profit earned by future value of the annuity for two years and the 1000 invested compounded for two years with the same interest rate:
Amount = P\(\left[1+\frac{r}{100}\right]^{n}\)
r = rate of interest,
n = number of years
P = principal
1000 [1.14]² = 1299.6
Future value of annuity after two years
= ₹ 1070
∴ Difference = ₹ 1299.6 – ₹ 1070
= ₹ 229.6