CBSE Sample Papers for Class 11 Applied Mathematics Term 2 Set 3 for Practice

Students can access the CBSE Sample Papers for Class 11 Applied Mathematics with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Applied Mathematics Term 2 Set 3 for Practice

Time : 2 Hours
Maximum Marks : 40

General Instructions:

• The question paper is divided into 3 sections -A, B and C.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study-based question. Internal choice has been provided in one question.

Section – A [2 Marks each]

Question 1.

Question 2.
Define direct and indirect taxes.

Question 3.
₹ 5,000 is invested in a Term Deposit Scheme that fetches interest 6% per annum compounded quarterly. What will be interest after one year ? What is effective rate of interest ? [(1.015)⁴ = 1.0613]
OR
Sachin deposited ₹ 1,00,000 in his bank for 2 years at simple rate of 6%. How much interest would he earn ? How much would be the final value of deposit ?

Question 4.
Reporting time of an employee is given below:

If the reporting time is 10 : 30 a.m., then find the probability of his coming late.

Question 5.
Find the equation of the line passing through (1, 2) and parallel to the line y = 3x – 1.

Question 6.
Determine n, if ²ⁿC₃: ^{nC₃ = 12 : 1.}

Section – B [3 Marks each]

Question 7.
A girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1,2,3 or 4, she tosses a coin two times and notes the number of heads obtained. If she obtained exactly two heads, what is the probability that she threw 1,2, 3 or 4 with the die ?

Question 8.
Find the equation of the circle which passes through (1, -2) and (4, – 3) and whose centre lies on the line 3x + 4y =

Question 7.
OR
Find the equation of circle which passes through the points (0, 2), (3, 0) and (3, 2). Find also the centre and radius of this circle.

Question 9.
A bag contains 8 red and 5 white balls. Two successive draws of all 3 balls are made at random from the bag without replacements. Find the probability that the first draw yields 3 white balls and second draw yields 3 red balls.

Question 10.
₹ 2 ,000 is invested at annual rate of interest of 10%. What is the amount after two years if compounding is done (a) annually (b) semi-annually (c) quarterly.

Section – C [4 marks each]

Question 11.
If all the word “MOTHER” are written in all possible orders and the word so formed are arranged in a dictionary order, then find the rank of word ‘MOTHER’ ?

Question 12.
Calculate the income tax payable by following individuals for the assessment year 2020-21: [U]

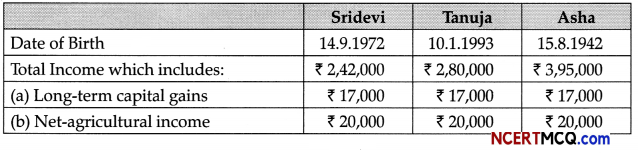
OR
Compute the tax liability of Mr. A (aged 42), having total income of ₹ 1,01,00,000 for AY 2020-21.

Question 13.
Find the derivative of x³ – 27 by the first principle method.

Question 14.
Read the following text and answer the following questions on the basis of the same:
At a point of time, people need only some currency for their day- to-day needs. For instance, workers who receive their salaries at the end of each month have extra cash at the beginning of the month.
What do people do with this extra cash? They deposit it with the banks by opening a bank account in their name. Banks accept the deposits and also pay an amount as interest on the deposits. In this way people’s money is safe with the banks and it earns an amount as interest.

Roshan invested ₹ 50,000 in bank at the rate of 10% per annum compounded annually.
On the basis of information given above, answer the following questions:
(a) What will be the interest for the first year and interest for the second year? (2)
(b) What is the difference between the simple interest and compound interest for the first year and for the first two years? (2)