CBSE Sample Papers for Class 11 Maths Term 2 Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 11 Maths with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Maths Term 2 Set 1 with Solutions

Time: 2 Hours
Maximum Marks:40

General Instructions:

• This question paper contains three sections A, B and C. Each part is compulsory.
• Section -A has 6 short answer type (SA1) questions of 2 marks each.
• Section -B has 4 short answer type (SA2) questions of 3 marks each.
• Section -C has 4 long answer type questions (LA) of 4 marls each.
• There is an internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A

Question 1.
If \(\frac{1}{6 !}+\frac{1}{8 !}=\frac{x}{9 !}\), find x
OR
If ⁿP₄ : ⁿP₂ = 12 : 1, find n (2)
Answer:

57 = \(\frac{x}{9}\)
x = 57 × 9 = 513
x = 513

OR

ⁿP₄ : ⁿP₂ = 12 : 1
\(\frac{n !}{(n-4) !}: \frac{n !}{(n-2) !}\) = 12 : 1
\(\frac{(n-2) !}{(n-4) !}\) = \(\frac{12}{1}\)
\(\frac{(n-2)(n-3)(n-4) !}{(n-4) !}\) = \(\frac{12}{1}\)
(n – 2)(n – 3) = 12
n² – 5n – 6 = 0
(n – 6)(n + 1) = 0
If n + 1 = 0
∴ n = – 1 is not possible (n ∈ N)
If n – 6 = 0
∴ n = 6

Question 2.
Write the eccentricity of the hyperbola, 9y² – 4x² = 36 (2)
Answer:

Question 3.
Differentiate: \(\frac{3 x+4}{5 x^{2}-7 x+9}\) (2)
Answer:

Question 4.
If sin A = \(\frac{3}{5}\) and \(\frac{\pi}{2}\) < A < π. Find cos A, tan 2A. (2)
Answer:
Since, sin A > 0 and \(\frac{\pi}{2}\) < A < π, then A is in II Quadrant.
sin A = \(\frac{3}{5}\) ⇒ sin² A = \(\frac{9}{25}\)
∴ cos² A = 1 – \(\frac{9}{25}\) = \(\frac{16}{25}\)
⇒ cos A = \(\frac{-4}{5}\) [in II Quadrant]
Now, tan A = \(\frac{\sin A}{\cos A}\) = \(\frac{3 / 5}{-4 / 5}\) = – \(\frac{3}{4}\)
and tan 2 A = \(\frac{2 \tan A}{1-\tan ^{2} A}\) = \(\frac{2(-3 / 4)}{1-(-3 / 4)^{2}}\) = \(\frac{-6 / 4}{7 / 16}\) = – \(\frac{24}{7}\)

Question 5.
Solve for x : \(\frac{2 x-3}{4}\) + 9 ≥ 3 + \(\frac{4 x}{3}\), x ∈ R (2)
Answer:

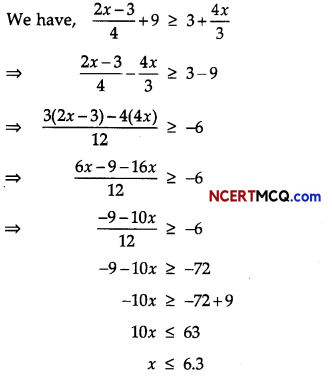
Question 6.
If the letters of the word ‘ALGORITHM’ are arranged at random in a row what is the probability the letter ‘GOR’ must remain together as a unit ?
OR
A card is selected from a pack of 52 cards. (2)
(i) What is the sample space?
(ii) Calculate the probability that card is an ace of spade?
Answer:
Number of letters in the word ‘ALGORITHM’ is 9
If ‘GOR’ remain together, then considered it as 1 number
∴ Number of letters = 6 + 1 = 7
Number of words, if ‘GOR’ remain together = 7!
Total number of words from the letters of the word ‘ALGORITHM’ = 9!
∴ Required probability
= \(\frac{7 !}{9 !}=\frac{7 !}{9 \times 8 \times 7 !}=\frac{1}{9 \times 8}=\frac{1}{72}\)

OR

(i) Sample space i.e. n(S) = 52
(ii) Number of ace of spade in a pack = 1
i.e. n(E) = 1
Probability that card is an ace = \(\frac{n(E)}{n(S)}=\frac{1}{52}\)

Section – B

Question 7.
If tan θ + sin θ = m and tan θ – sin θ = n, then prove that: m² – n² = 4sinθ.tan θ (3)
Answer:
Given, tan θ + sin θ = m and tan θ – sin θ = n,
To prove, m² – n² = 4 sin θ tan θ
L.H.S. = m² – n²
= (m + n) (m – n)
= [(tan θ + sin θ) + (tan θ – sin θ)]. [(tan θ + sin θ) – (tan θ – sin θ)]
= (2 tan θ) (2 sin θ)
= 4 sin θ tan θ
= R.H.S

Question 8.
Find the co-ordinate of the vertices, foci eccentricity and length of latus rectum of the hyperbola
\(\frac{x^{2}}{25}-\frac{y^{2}}{4}\) = 1
OR
Find the distance between the directrices of the hyperbola x² – y² = 8. (3)
Answer:

Commonly Made Error: Many students get confused between the equation of ellipse and hyperbola. They write equation of ellipse when asked of hyperbola.

Answering Tip: Learn equation of hyperbola and terms related to it. Understand the equation and its properties with the help of its diagram which will help you to remember long.

OR

Given equation of the parabola is
x² – y² = 8.

Question 9.
If tan (A + B) = p, tan (A – B) = q, then show that: tan 2A = \(\frac{p+q}{1-p q}\) (3)
Answer:
Given, tan (A + B) = p, and tan (A-B) – q,
L.H.S. = tan2A = tan (A + B + A – B)
= tan [(A + B) + (A – B)]
= \(\frac{\tan (A+B)+\tan (A-B)}{1-\tan (A+B) \cdot \tan (A-B)}\)
= \(\frac{p+q}{1-p q}\)
= R.H.S.
Hence proved.

Question 10.
From a group of 7 boys and 5 girls, a team consisting of 4 boys and 2 girls is to be made. In how many different ways it can be done? (3)
Answer:
From a group of 7 boys, 4 boys can be choose in ⁷C₄ ways.
From a group of 5 girls, 2 girls can be choose in ⁵C₂ ways.
∴ Required number of ways to choose a team consisting 4 boys and 2 girls are
= ⁷C₄ × ⁷C₄
= \(\frac{7 !}{3 ! 4 !} \times \frac{5 !}{3 ! 2 !}\)
= \(\frac{7 \cdot 6 \cdot 5}{3 \cdot 2 \cdot 1} \times \frac{5 \cdot 4}{2 \cdot 1}c\)
= 35 × 10
= 350

Section – C

Question 11.
Find the derivative of the functions \(\frac{a}{x^{4}}-\frac{b}{x^{2}}\) + cos x where a and b are non-zero constant. (4)
Answer:
Let f(x) = \(\frac{a}{x^{4}}-\frac{b}{x^{2}}\) + cos x

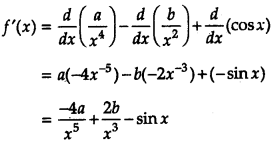
Question 12.
Find the equation of a circle passing through the point (7, 3) having radius 3 units and whose centre lies on the line y = x – 1.
OR
Find the equation of a circle whose centre is (3, – 1) and which cuts off a chord length 6 units on the line 2x – 5y + 18 = 0. (4)
Answer:
Let equation of circ1e be
(x – h)² + (y – k)² = r²
⇒ (x – h)² + (y – k)² = 9 …(i)
Now, the circ1e passes through the point (7, 3)
∴ (7 – h)² + (3 – k)³ = 9 …(ii)
⇒ 49 – 14h + h² + 9 – 6k + k² = 9
⇒ h² + k² – 14h – 6k + 49 = 0 …(iii)
Now, y = x – 1, k = h – 1
On putting k = h – 1 in Eq. (iii), we get
h² + (h – 1)² – 14h – 6(h -1) + 49 = 0
⇒ h² + h² – 2h + 1 – 14h – 6h + 6 + 49 = 0
⇒ 2h² – 22h + 56 = 0
⇒ h² – 11h + 28 = 0
⇒ h² – 7h – 4h + 28 = 0
⇒ h(h – 7) – 4(h – 7) = 0
⇒ (h – 7)(h – 4) = 0
∴ h = 4, 7
When h = 7 then k = 7 – 1 = 6
∴ Centre (7, 6)
When h = 4 then h = 3
∴ Centre = (4, 3)
So, the equation of circ1e when centre (7, 6), is
(x – 7)² +(y – 6)² = 9
⇒ x² – 14x + 49 + y² – 12y + 36 = 9
⇒ x² + y² – 14x – 12y + 76 = 0
when centre (4,3), then the equation of circle is,
(x – 4)² + (y – 3)² = 9
⇒ x² – 8x + 16 + y² – 6y + 9 = 9
⇒ x² + y² – 8x – 6y + 16 = 0

OR

Given, centre of the circle is (3, -1),

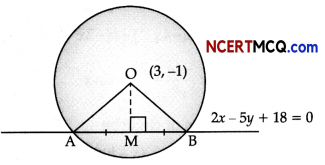
Now, OM = \(\left|\frac{6+5+18}{\sqrt{4+25}}\right|\) = \(\frac{29}{\sqrt{29}}\) = √29 units
In ∆OMB, OB² = OM² + AB² [∵ AB = 6 ⇒ AM = MB = \(\frac{1}{2}\), AB = 3]
⇒ OB² = 29 + 9
⇒ OB² = 38 units
So, the radius of circle is √38 units
∴ Equation of the circle with radius
r = √38 units and centre (3, -1) is
⇒ (x – 3)² + (y + 1)² = 38
⇒ x² – 6x + 9 + y² + 2y + 1 = 38
x² + y² – 6x + 2y = 28
x² + y² – 6x + 2y – 28 = 0

Question 13.
Solve the following system of inequalities graphically (4)
2x + y ≤ 24,
x + y ≥ 11,
2x + 5y ≤ 40, x, y ≥ 0.
Answer:
Inequality (x > 0) represents the region on the right of Y-axis and Y-axis itself. Inequality (y > 0) represents the region above X-axis and X-axis itself.
2x + y ≤ 24 …(i)
x + y ≥ 11 …(ii)
2x + 5y ≤ 40, x, y ≥ 0 …(iii)
We first draw the graph of lines
2x + y = 24, x + y = 11 and 2x + 5y = 40
Now, 2x + y = 24, passes through A(12, 0) and B(0, 24)
Again, x + y = 11, passes through C(11, 0) and D(0, 11)

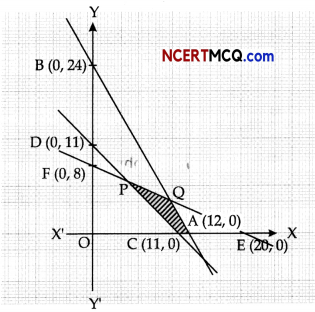
Further 2x + 5y = 40, passes through E(20, 0) and F( 0,8)
Shaded area PQAC is the solution area.

Commonly Made Error: Many students get confused to find the common (Feasible) region. They must have proper knowledge on intercept form of equation and coordinate geometry. They should have know how to handle inequations.

Answering Tip: The points of the line are also included in the solution of the inequality and the graph of the inequality lies below or above the graph of the equation.

Case-Based/Data Based

Question 14.
One of the four persons John, Rita, Aslam or Gurpreet will be promoted next month. Consequently the sample space consists of four elementary outcomes S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}. You are told that the chances of John’s promotion is same as that of Gurpreet, Rita’s chances of promotion are twice as likely as Johns. Aslam’s chances are four times that of John.

Based on the given information, answer the following questions:
(i) What is the probability that John got promoted? (2)
(ii) If A = {John promoted or Gurpreet promoted}, Find P(A). (2)
Answer:
Let Event:
J = John promoted
R = Rita promoted
A = Aslam promoted
G = Gurpreet promoted
Given sample space, S = {John promoted, Rita promoted, Aslam promoted, Gurpreet promoted}
i.e., S = {J, R, A, G)
It is given that, chances of John’s promotion is same as that of Gurpreet.
P(J) = P(G)
Rita’s chances of promotion are twice as likely as John.
P(R) = 2P(J)
and Aslam’s chances of promotion are four times that of John.
P(A) = 4P(J)

(i) P(J) + P(R) + P(A) + P(G) = 1
⇒ P(J) + 2P(J) + 4P(J) + P(J) = 1
⇒ 8P(J) = 1
P(J) = P(John Promoted) = \(\frac{1}{8}\)

(ii) A = John promoted or Gurpreet promoted
∴ A = J ∪ G
P(A) = P(J ∪ G)
∴ P(A) = P(J) + P(G) – P(J ∩ G)
P(A) = \(\frac{1}{8}+\frac{1}{8}\) – 0 [∵ P(J ∩ G) = 0]
= \(\frac{1}{4}\)