CBSE Sample Papers for Class 11 Maths Term 2 Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 11 Maths with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 11 Maths Term 2 Set 2 with Solutions

Time: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections A, B and C. Each part is compulsory.
• Section -A has 6 short answer type (SA1) questions of 2 marks each.
• Section -B has 4 short answer type (SA2) questions of 3 marks each.
• Section -C has 4 long answer type questions (LA) of 4 marls each.
• There is an internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A

Question 1.
A wheel makes 360 revolutions in 1 min. Through how many radians does it turn in 1 second.
OR
Find the degree measure of the angle subtended at the centre of circle of radius 100 cm by an arc of 22 length 22 cm. (Use π = \(\frac{22}{7}\))
Answer:
No. of revolution in one minute = 360
∴ No. of revolutions m one second = \(\frac{360}{2}\)
= 6

∴ 6 revolutions = 6 × 2π = 12π radians
Hence, no. of radians turned in one second = 12π
OR
Given, l = length of arc = 22 cm
r = radius of circle = 100 cm
Let θ be the angle subtended at the centre, then

Question 2.
If parabola y² = px passes through point (2, -3), find the length of latus rectum. (2)
Answer:
Given equation of parabola is y² = px …(i)
Since (i) passes through (2, -3).
∴ (-3)² = p.2
⇒ p = \(\frac{9}{2}\)
∴ y² = \(\frac{9}{2}\)x
⇒ y² = 4. \(\frac{9}{8}\)x
Comparing above by y² = 4ax
a = \(\frac{9}{8}\)
∴Length of latus rectum = 4a = \(\frac{9}{2}\) units

Commonly Made Error:
Students make mistakes while comparing the given equation with the general form of parabola.

Answering Tip:
Learn the equations of parabola and the terms released it. Understand the equation and its properties with the help of its diagram.

Question 3.
How many 5 digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once?
OR
Determine the number of 5 card combining out of deck of 52 cards if each selection of 5 cards has exactly one king. (2)
Answer:
Number of ways to fill the III place = 8
Number of ways to fill the IV place = 7

Number of ways to fill the V place = 6
Hence, total number of ways = 8 × 7 × 6 = 56 × 6 = 336
OR
1 king out of 4 kings can be selected in ⁴C₁ ways
Remaining 4 cards out of remaining 48 cards can be selected in ⁴C₄ ways.
Hence, total number of ways
= ⁴C₁ × ⁴⁸C₄ = 4 × ⁴⁸C₄

Question 4.
Given P(A) = \(\frac{3}{5}\) and P(B) = \(\frac{1}{5}\). Find P(A ∪ B) if A and B are mutually exclusive events. (2)
Answer:
P(A) = \(\frac{3}{5}\), P(B) = \(\frac{1}{5}\)
A and B are mutually exclusive events
∴ P(A ∩ B) = 0
Now P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{3}{5}+\frac{1}{5}\) – 0
P(A ∪ B) = \(\frac{4}{5}\) = 0.8

Question 5.
Solve the inequality: -3 ≤ 4 – \(\frac{7x}{2}\) ≤ 18 (2)
Answer:
The given inequality -3 ≤ 4 – \(\frac{7x}{2}\) ≤ 18 Adding (-4) to each term,
-3 – 4 ≤ 4 – \(\frac{7x}{2}\) – 4 ≤ 18 – 4
-7 ≤ – \(\frac{7x}{2}\) ≤ 14

Multiplying by (\(\frac{-2}{7}\)) to each term

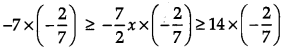
⇒ 2 ≥ x ≥ -4
⇒ 4 ≤ x ≤ 2
∴ Solution set = [-4, 2]

Question 6.
Find the derivatives of 2x – \(\frac{3}{4}\) (2)
Answer:
Let f(x) = 2x – \(\frac{3}{4}\)
∴ f'(x) = \(\frac{d}{d x}\)(2x – \(\frac{3}{4}\))
= 2\(\frac{d}{d x}\)x – \(\frac{d}{d x}\)(\(\frac{3}{4}\))
= 2 × 1 – 0
= 2

Section – B

Question 7.
Find the centre and radius of the circle 2x² + 2y² – x = 0. (3)
Answer:
Given equation of the circle is
2x² + 2y² – x = 0

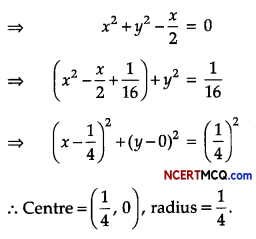
Question 8.
Prove that: \(\frac{\cos 4 x \sin 3 x-\cos 2 x \sin x}{\sin 4 x \cdot \sin x+\cos 6 x \cdot \cos x}\) = tan 2x (3)
OR
Prove that:
tan α. tan (60° – α) . tan (60° + a) = tan 3α (3)
Answer:

Commonly Made Error:
Many students get confused among the formula of trigonometry. They must learn all the formulae properly and practise the derivation of the formula to avoid mistake.

Answering Tip:
Simplification of trigonometric equations needs sufficient practice. Give ample practice such type of questions.

OR

L.H.S = tan α. tan (60° – α). tan (60° + a)

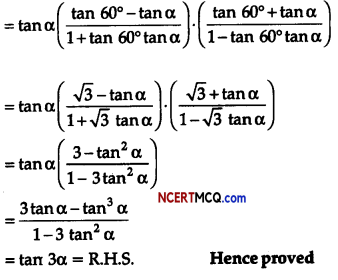
Question 9.
From a class of 40 students, in how many ways can five students be chosen for an excursion party. (3)
Answer:
From a dass of 40 students, five students can be chosen for an excursion party in ⁴C₅ ways

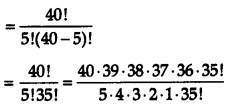
= 658,008

Question 10.
Find the value of the expression
3[sin⁴(\(\frac{3 \pi}{2}\) – α) + sin⁴(3π + α)] – 2[sin⁶(\(\frac{\pi}{2}\) + α) + sin⁶(5π – α)]
Answer:
Given 3[sin⁴(\(\frac{3 \pi}{2}\) – α) + sin⁴(3π + α)] – 2[sin⁶(\(\frac{\pi}{2}\) + α) + sin⁶(5π – α)]

= 3[cos⁴α + sin⁴(π + α)] – 2[cos⁶ α + sin⁶(π – α)]
= 3(cos⁶α + sin⁶α] – 2[cos⁶ α + sin⁶α]
= 3(cos⁴α + sin⁴ α + 2sin²α cos²α – 2sin²α cos²α] – 2(cos²α + sin²α)³ – 3cos²α sin²α(cos²α + sin²α)]
= 3[(cos²α + sin²α)² – 2sin²αcos²α] -2[1 – 3cos²αsin²α]
= 3(1 – 2sin²αcos²α – 2 + 6cos²αsin²α]
= 3 – 6sin²αcos²α – 2 + 6sin²αcos²α
= 1

Section – C

Question 11.
Using first principle find the derivative of x cos x function: (4)
Answer:
Let f(x) = x cos x
∴ f(x + h) = (x + h)cos(x + h)

Question 12.
A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there is 460 L of the 9% solution, how many litres of 3% solution will have to be added?
OR
A solution is to be kept between 40°C and 45°C. What is the range of temperature in degree Fahrenheit, if the conversion formula is F = \(\frac{9}{5}\)C +32? (4)
Answer:
Let x L of 3% solution be added to 460 L of 9% solution of acid.
Then, total quantity of mixture = (460 + x) L
Total add content in the (460 + x) L of mixture
= (460 × \(\frac{9}{100}\) + x × \(\frac{3}{100}\))L
It is given that add content in the resulting mixture must be more them 5% but less than 7%.
Therefore,

⇒ 2300 + 5x < 4140 + 3x < 3220 + 7x
Taking first two inequalities,
2300 + 5x < 4140 + 3x
⇒ 5x – 3x < 4140 – 2300
⇒ 2x < 1840
⇒ x < \(\frac{1840}{2}\)
⇒ x < 920 …(i)
Taking last two inequalities,
4140 + 3x < 3220 + 7x
⇒ 3x – 7x < 3220 – 4140
⇒ -4x < -920 ⇒ 4x > 920
⇒ x > \(\frac{920}{4}\)
⇒ x > 230 …(ii)
Hence, the number of litres of the 3% solution of add must be more than 230 L and less than 920 L.

OR

Let the required temperature be x° F.
Given that, F = \(\frac{9}{5}\)C + 32
⇒ 5F = 9C + 32 × 5
⇒ 9C = 5F – 32 × 5
∴ C = \(\frac{5 F-160}{9}\)
Since, temperature in degree Celsius lies between 40°C to 45°C.
Therefore, 40 < \(\frac{5 F-160}{9}\) < 45
40 < \(\frac{5 F-160}{9}\) < 45
⇒ 40 × 9< 5x – 160 < 45 × 9 [multiplying throughout by 9]
⇒ 360 < 5x – 160 < 405 [adding 160 throughout]
⇒ 360 + 160 <5x< 405+160
⇒ 520 < 5x < 565 1
⇒ \(\frac{520}{5}\) < x < \(\frac{565}{5}\) [divide throughout by 5]
⇒ 104 < x < 113
Hence, the range of temperature in degree Fahrenheit is between 104 °F to 113°F.

Question 13.
If A and B be the points (3,4,5) and (-1,3, -7), respectively, find the equation of the set of points P such that PA² + PB² = k², where k is constant. (4)
Answer:
The coordinates of points A and B are given as (3, 4, 5) and (-1, 3, -7) respectively. Let the co-ordinates of point P be (x, y, z).
On using distance formula, we obtain
PA² = (x – 3)² + (y – 4)² + (z – 5)²
= x² + 9 – 6x + y² + 16 – 8y + z² + 25 – 10z
= x² + y² + z² – 6x – 8y – 10z + 50

PB² = (x + 1)² + (y – 3)² + (z + 7)²
= x² + 1 + 2x + y² + 9 – 6y + z² + 49 + 14z
= x² + y² + z² + 2x – 6y + 14z + 59

Now, if PA² + PB² = k², then
(x² + y² + z² – 6x – 8y – 10z + 50) + (x² + y² + z² + 2x – 6y + 14z + 59)
⇒ 2x² + 2y² + 2z² – 4x – 14y + 4z + 109 = k²
⇒ 2(x² + y² + z² – 2x – 7y + 2z) + 109 = k²
⇒ 2(x² + y² + z² – 2x – 7y + 2z) = k² -109
⇒ x² + y² + z² – 2x – 7y + 2z = \(\frac{k^{2}-109}{2}\)
Thus, the required equation is
x² + y² + z² – 2x – 7y + 2z = \(\frac{k^{2}-109}{2}\)

Case-Based/Data Based

Question 14.
A child’s game has 8 triangles of which 3 are blue and rest are red, and 10 squares of which 6 are blue and rest are red. One piece is lost at random.

(i) Find the probability that lost piece is triangle. (2)
Answer:
Since, total no. of triangles = 8
Triangles with blue colour = 3
Triangles with red colour = 8 – 3 = 5 and
total no. of squares = 10
Squares with blue colour = 6
Squares with red colour = 10 – 6
= 4

Number of favourable outcomes for the event that lost figure is triangle,
i.e., F (E) = 8
Total figures (square and triangle)
= 8 + 10 = 18
i.e., T(E) = 18

Probability (getting a triangle),
P(E) = \(\frac{F(E)}{T(E)}\)
= \(\frac{8}{18}=\frac{4}{9}\)

(ii) Find the probabilities that lost piece is square of blue colour & triangle of red colour. (2)
Answer:
Number of favourable outcomes for the events that lost figure is square of blue colour, i.e., F(E) – 6 and T(E) = 18
∴ P(getting a blue square),
P(E) = \(\frac{F(E)}{T(E)}\)
= \(\frac{6}{18}=\frac{1}{3}\)
Number erf favourable outcomes for the event that lost figure is triangle of red colour = 5,
i.e., F(E) = 5 and
T(E) = 18

∴ P(lost figure is red triangle),
P(E) = \(\frac{5}{18}\)