CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 1 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
The marginal revenue function for a commodity is given by MR = 9 + 2x – 6x². Find the demand function.
Or
The marginal cost of producing x pairs of tennis shoes is given by MC = 50 + \(\frac{300}{x+1}\)
If the fixed cost is ₹ 2000, find the total cost function.
Answer:
We have, MR = 9 + 2x – 6x²
We know that \(\frac{dR}{dx}\) = MR
⇒ R = ∫ MR dx + k
⇒ R = ∫(9 + 2x – 6x²)dx + k
⇒ R = 9x + x² – 2x³ + k
When, x = 0, R = 0, we get k = 0, R = 9x + x² – 2x³

Demand function, p = \(\frac{R}{x}\)
When, x = 0, R = 0, we get k = 0
∴ R = 9x + x² – 2x³

Demand function, p = \(\frac{R}{x}\)
∴ p = \(\frac{9 x+x^{2}-2 x^{3}}{x}\) = 9 + x – 2x²
We have, MC = 50 + \(\frac{300}{x+1}\)
∫ dC = ∫MC dx + K [∵ \(\frac{d C}{d x}\) = MC]
∫ C = ∫ (5o+ \(\frac{300}{x+1}\))dx + K
C = 50x + 300log(x + 1) + K …(i)

When x =0, C = 2000, we get K = 2000
∴ C = 50x + 300log(x + 1) + 2000 [from Eq. (i)]

Hence, total cost function is
50x + 300 log(x + 1) + 2000.

Question 2.
Find the present value of perpetuity of ₹ 600 at end of each quarter, if money is worth 8% compounded quarterly.
Answer:
Given, R = ₹ 600
let P be the present value of the perpetuity
Also, given rate of interest is quarterly, then
i = \(\frac{R}{4}\)% ⇒ i = \(\frac{8}{400}\)
∴ P = \(\frac{R}{i}=\frac{600}{\frac{8}{400}}=\frac{600 \times 400}{8}\) = 3000
Hence1 P is ₹ 30000.

Question 3.
What effective rate is equivalent to a nominal rate of 8% per annum compounded quarterly? [given (1.02)⁴ = 1.0824]
Or
Find the present value of an annuity of ₹ 1000 payable at the end of each year for 5 years, if money is worth 6% compounded annually, [given (1.06)^-5 = 07473]
Answer:
We have, r = 8% = \(\frac{8}{100}\) and in = 4
∴ r_e = \(\left(1+\frac{r}{m}\right)^{m}\) – 1
⇒ r_e = \(\left(1+\frac{8}{400}\right)^{4}\) – 1
⇒ r_e = (1 + 0.02)⁴ = (1 .02)⁴ – 1
⇒ r_e = 1.0824 – 1 = 0.0824
Hence, effective rate is (0.0824 × 100)% = 8.24%
Or
Given R = ₹ 1000, i = 6% = 0.06 and n = 5

Hence, present value of ordinary annuity is ₹ 4211.67

Question 4.
A sampling distribution of the sample means X̄ is formed from a population with mean weight µ = 60 kg and standard deviation σ = 9 kg. What is the expected value and standard deviation of X̄, if sample size is 36?
Answer:
Given, mean weight of population (µ)= 60 kg
Standard deviation (σ) = 9 kg
Expected value of X̄ i.e. E(X̄) = g
∴ E(X̄) = 60 kg
SD(X̄) = \(\frac{\sigma}{\sqrt{n}}=\frac{9}{\sqrt{36}}\) [∵n = sample size = 36]
SD(X̄) = \(\frac{9}{6}\) = 1.5 kg

Question 5.
Find the trend values using 3-yearly moving average for the loans sanctioned to farmers by a particular branch of a bank in a village.

Answer:
Calculation of 3-yearly moving average

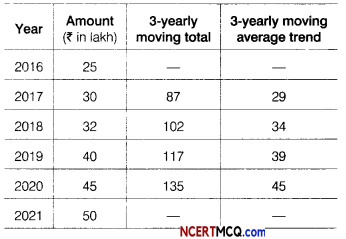
Question 6.
The feasible region of the LPP minimum Z = 3x + 2y
Subject to constraints are
2x + y ≥ 6, x – y ≥ 0, x ≥ 0, y ≥ 0 is given below:

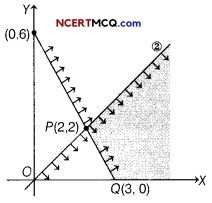
Determine the optimal solution. Justify your answer.
Answer:
We have, Minimum Z = 3x + 2y
Subject to constraints are
2x + y ≥ 6, x – y ≥ 0, x ≥ 0, y ≥ 0

The feasible region of the constraints is given below.

Corner point	Value of Z =3x + 2y
P(2,2)	3 × 2 + 2 × 2 = 6 + 4 = 10
Q(3, 0)	3 × 3 + 2 × 0 = 9 + 0 = 9

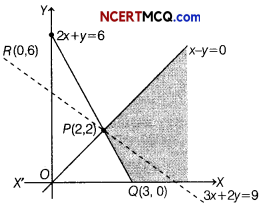
The smallest value of Z is 9. Since, the feasible region is unbounded, we draw the graph of 3x + 2y < 9. The resulting open half plane has common point with feasible region.
∴ Z = 9 is not the minimum value of Z. Hence, the optimal solution does not exist.

Section -B [12 Marks]

Question 7.
The supply function for a commodity is given by p = x² + 4x + 3, where x is the quantity supplied at the price p. Find the producers surplus when the price of the commodity is ₹ 48.
Answer:
The supply function is given by p = x² + 4x+3
It is given that p₀ = 48

Putting the value of p₀ in p = x² + 4x + 3
⇒ 48 = x² + 4x₀ + 3
⇒ x² + 4x₀ – 45 = 0
⇒ (x₀ + 9)(x₀ – 5) = 0
⇒ x₀ = 5 and x₀ ≠ – 9 [∵ x ≥ 5]

We know that producer surplus,

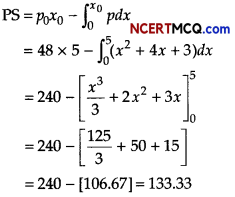
Hence, produce surplus is ₹ 133.33.

Question 8.
The following table shows the quarterly sales (₹ in crore) of a real estate company. Compute the trend by quarterly moving averages.

Or
Fit a straight line trend by the method of least squares and estimate the trend for the year 2023.

Answer:
The trend value are given by 4-quarterly centered moving average.

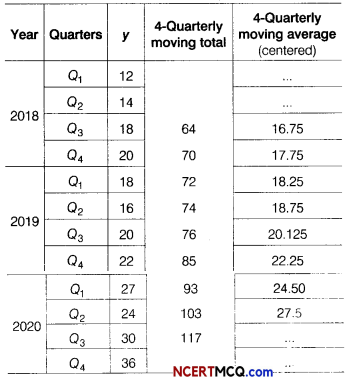
Here, n = 7 (odd)
So, middle year i.e 2017 takes as origin. Construct the table as under

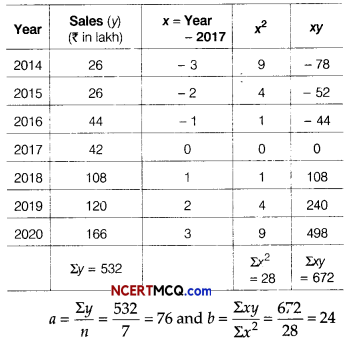
y_t = a + bx and y_t = 76 + 24x

Estimated sales = y_t for 2023 = 76 + 24 × 6
= ₹ 220 lakh

Question 9.
A machine produces washers of thickness 0.50 mm. To determine whether the machine is in proper working order, a sample of 10 washers is chosen for which the mean thickness is 0.53 mm and the standard deviation is 0.03 mm. Test the hypothesis at 5% level of significance that the machine is working in proper order.
[given t_0.025 = 2.262 at v = 9]
Answer:
It is given that,
p = Population mean = 0.50 mm
X̄ = Sample mean = 0.53 mm
n = Sample size = 10
and S = Sample standard deviation = 0.03 mm

We define null hypothesis H₀ and alternative hypothesis H₁, as follows
H₀ : µ = 0.50 mm
µ₁ : µ ≠ 0.50 mm

Thus, a two-tailed test is applied under hypothesis H0, we have
t = \(\frac{\bar{X}-\mu}{S} \sqrt{(n-1)}=\frac{0.53-0.50}{0.03}\) × 3 = 3

Since, the calculated value of f = 3 does not lie in the internal – t_0.025 to t_0.025 i.e. – 2.262 to 2.262 for 10 – 1 = 9 degree of freedom. So, we reject H₀ at 0.05 level. Hence, we conclude that machine is not working properly.

Question 10.
A person invested ₹ 15000 in a mutual fund and the value of investment at the time of redemption was ₹ 25000. If CAGR for this investment is 8.88%, calculate the time period for which the amount was invested?
[given log(1.667) = 0.2219 and log(1.089) = 0.037]
Answer:
Given, Begining value (BV) = ₹ 15000
Ending valne (EV) = ₹ 25000
Let number of years = n and CAGR = 8.88%

We Know that

Hence, time period is 6 yr.

Section – C [16 Marks]

Question 11.
S & D chemicals produces two products, an alkaline solution and a base oil that are sold as raw material to companies manufacturing soaps and detergents. On the basis of current inventory levels and estimated demand for the coming month, S & D’s management has decided that combined production of alkaline solution and base oil must be at least 3500 gallons. S & D chemicals are also committed to supply 1250 gallons of alkaline solution to one of its major customer. The alkaline solution and base oil requires respectively 2 h and 1 h of processing time per gallon. The total processing time available for the coming month is 6000 h. The production cost is ₹ 200 per gallon for the alkaline solution and ₹ 300 per gallon for base oil.
Formulate the above as a LPP and solve it by graphical method to help S & D chemicals determine the minimum production cost.
Answer:
Let the company produces x and y gallons of
alkaline solution and base oil respectively, also let C be the production cost.
Minimum Z = 200x + 300y
Subject to constraints are
x + y ≥ 3500 ……….(i)
x ≥ 1250 …….(ii)
2x + y ≤ 6000 ………(iii)
x, y ≥ 0 …….(iv)

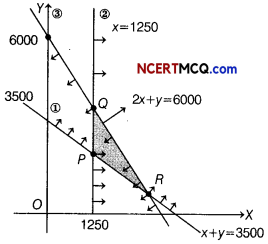
Corner Points	Value of Z = 200x + 300y
P(1250, 2250)	925000
Q(1250, 3500)	1300000
R(2500, 1000)	800000 (Minimum)

Minimum cost is ₹ 800000 when 2500 gallons of alkaline solutions and 1000 gallons of base oil are manufactured.

Question 12.
A machine costing ₹ 50000 is to be replaced at the end of 10 yr, when it will have a salvage value of ₹ 5000. In order to provide money at that time for a machine costing the same amount, a sinking fund is set up. If equal payments are placed in the fund at the end of each quarter and the fund earns 8% compounded quarterly, then what should each payment be? [given (1.02)40 = 2.208]
Answer:
We have, cost of machine = ₹ 50000
Salvage value of machine = ₹ 5000
Hence, the money required for new machine after 10 yr = ₹ (50000 – 5000) = ₹ 45000
So, we have S = ₹ 45000, i = \(\frac{8}{400}\) = 0.02 and
n = 10 × 4 = 40

Hence, ₹ 745.03 are set aside each year to purchase new machine.

Question 13.
A couple wishes to purchase a house for ₹ 1500000 with a down payment of ₹ 400000. If they can amortize the balance at an interest rate 9% per annum compounded monthly for 10 yr, find the monthly installment (EMI). Also, find the total interest paid.
[given, (1.0075) ^-120 = 0.4079]
Or
A ₹ 2000, 8% bond is redeemable at the end of 10 yr at ₹ 105. Find the purchase price to yield 10% effective rate, [given (1.1)^-10 = 0.3855]
Answer:
We have, cost of house = ₹ 1500000
Down payment ₹ 400000
∴ Balance amount = Cost of house – Down payment
= ₹ (1500000 – 400000)
= ₹ 1100000

Hence, EMI is ₹ 13933.50.
∴ Total interest paid = n(EMI) – P
= 120 × 13933.50 – 1100000
=1672020- 1100000= 572020

Hence, total interest paid is ₹ 572020
Or
Given, face value of bond = ₹ 2000

Number of periods = 10
i = annual yield rate – 10% = \(\frac{10}{100}\) = 0.1

Redemption value C = 1.05 × 2000 = ₹ 2100
R Annual dividend = 2000 × 8%
= 2000 × \(\frac{8}{100}\) = ₹ 160

Let V be the purchase price of the bond, then

Hence, purchase price of bond is ₹ 1792

Case Based/Data Based

Question 14.
General anesthesia is used for major operations to cure the patients and conduct pain free surgeries. Propofol is a commonly used anesthetic injected for major operations such as knee replacement or open heart surgery. It also acts as a sedative and an analgesic.

A patient is rushed to operation theatre for a 2-hour cardiac surgery. A person is anesthetized when its blood stream contains at least 3 mg of propofol per kg of body weight. The rate of change of propofol (x), in the body is proportional to the quantity of propofol present at that time. Based on the above information.

Answer the following questions:
(i) Show that propofol given intravenously is eliminated exponentially from the patients’ blood stream.
Answer:
Let x denotes the quantity of propofol present in body at any time t

⇒ x = e^-kt+C
⇒ x = e^C e^-kt = Ae^-kt [∵ e^c = A]

Let x = x₀ at t = 0
∴ x₀ = Ae⁰
⇒ A = x₀

∴ x = x₀e^-kt, where x₀ = original quantity

(ii) What dose of propofol should be injected to induce unconsciousness in a 50 yr adult for a two hours operation? [given (2)^1/5 = 1.1487 and assume half-life of propofol = 5 h]
Answer:
Now, x = x₀e^-kt
When x = \(\frac{x_{0}}{2}\) and t = 5, we get
\(\frac{x_{0}}{2}\) = x₀e^-kt
⇒ e^-5k = \(\frac{1}{2}\)
⇒ e^k = (2)^1/5

The quantity of propofol needed in 50 yr adult after 2 h = 50 × 3 = 150 mg

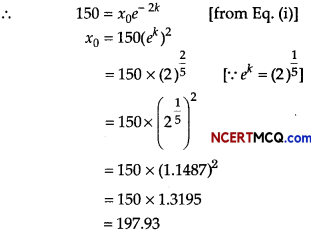
∴ Required dose is 197.93 mg