CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 10 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 10 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 10 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
The marginal revenue function of a commodity is given by MR = 6 – 5x + x².
Find the demand function.
Or

Answer:
We have, MR = 6 – 5x + x²
Now, R = ∫(MR) dx + K
= ∫(6 – 5x + x²)dx + K
= 6x – \(\frac{5 x^{2}}{2}\) + \(\frac{x^{3}}{3}\) + k
When x = 0, then R = 0.
∴ K = 0
Thus, R = 6x – \(\frac{5}{2}\)x² + \(\frac{x^{3}}{3}\) and the
corresponding demand function is given by

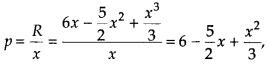
where p is the price, when the number of units sold x.

OR

Here, redefined the given integrand in given interval (0, 4).
For, 0 < x < 4, |x| = x
0 < x ≤ 2 , |x – 2| = – (x – 2)
2 ≤ x < 4 , |x – 2| = (x – 2)
0 < x < 4, |x – 4| = – (x – 4)

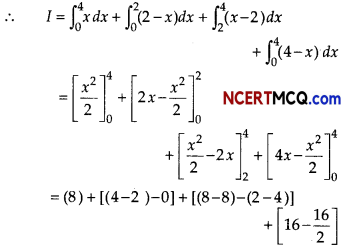
= 8 + 2 + 2 + (16 – 8)
= 8 + 2 + 2 + 8 = 20

Question 2.
A group of 5 patients treated with medicines P weigh 10, 8, 12, 6, 4 (in kg). Second group of 7 patients treated with medicine Q weigh 14, 12, 8,10, 6, 2,11 (in kg). Comment on rejection of hypothesis with significance level 5%. [given, t_(10,0.05) = 1.812]
Answer:
Consider,
H₀: µ₁ = µ₂ and H₁: µ₁ > µ₂
[where, µ₁ and µ₂ denotes population means for given two groups]


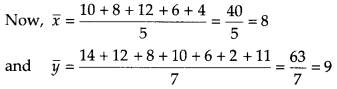
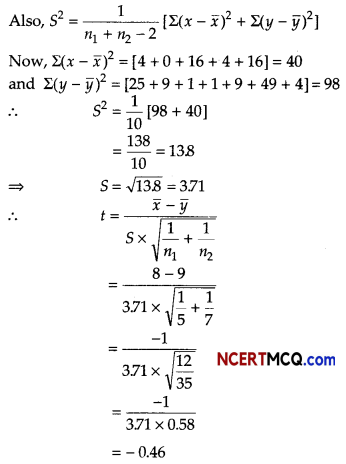
Given, t_(10,0.05) = 1812
Since, t_cal value < t_tab value
Hence, null hypothesis (H₀) may be accepted with 5% significance.

Question 3.
A machine, the useful life of which is estimated to be 12 yr, cost ₹ 15000. Calculate the scrap value at the end of its life, depreciation being charged at 8% per annum [given, (0.92)¹² = 0.3676].
Or
What sum of money is needed to invest now, so as to get ₹ 8000 at the beginning of every month forever, if the money is worth 6% per annum compounded monthly?
Answer:
We have,
C = ₹ 15000, n = 12 yr and r = 8% = 0.08.
We know that S = C (1 – r)ⁿ
S = 15000(1 – 0.08)¹²
= 15000 (0.92 )¹²
= 15000 × 0.3676
= ₹ 5514
∴ The scrap value is ₹ 5514.

Or

Given, R = ₹ 8000 and r = \(\frac{6}{12}\) % = 0.5% per month.
So, i = \(\frac{0.5}{100}\) = 0.005
The given annuity is a perpetuity of second type.
So, P = R + \(\frac{R}{i}\) = 8000 + \(\frac{8000}{0.005}\)
= 8000 + 1600000
=1608000
Hence, ₹ 1608000 are needed to invest now to get ₹ 8000 at the beginning of every month forever

Question 4.
A firm has to transport 1200 packages using large vans, which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is ₹ 400 and each small van is ₹ 200. Not more than ₹ 3000 is to be spent on the job and the number of large vans cannot exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
Answer:
Let the firm has x number of large vans and y number of small vans. From the given information, we have following corresponding constraint table.

Thus, we see that objective function for minimum cost is Z = 400 x + 200y.
Subject to constraints are,
200x + 80y ≥ 1200 [package constraint]
⇒ 5x + 2y ≥ 30 …(i)
and 400x + 200y ≤ 3000 [cost constraint]
⇒ 2x + y ≤ 15 …(ii)
and x ≤ y [van constraint] …(iii)
and x ≥ 0, y ≥ 0
[non-negative constraints] …(iv)
Thus, required LPP to minimise cost is minimise Z = 400x + 200y
Subject to constraints are,
5x + 2y ≥ 30, 2x + y ≤ 15, x ≤ y, x ≥ 0 and y ≥ 0

Question 5.
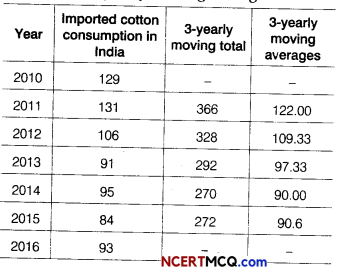
Construct 3-yearly moving averages from the following data.

Answer:
Calculate of 3-yearly moving averages

Question 6.
Find the effective rate that is equivalent to a nomial rate of 8% compounded semi-annually.
Answer:
We have,

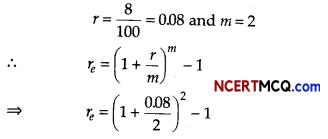
⇒ r_e = (1 + 0.04)² – 1
⇒ r_e = (1.04)² – 1
= 1.0816 – 1
= 0.0816
Hence, the effective rate is 8.16%.

Section – B [12 marks]

Question 7.
The time series given below shows the number of TV sold by a company since 2003.

Find the linear equation that describes the trend in the number of TV sold.
Also, estimate the sale of TV in 2014.
Answer:
Here, n = 10 (even)
So, origin is mean of two middle years
i.e., \(\frac{2007+2008}{2}\) = 2007.5

Table for fitting linear equation

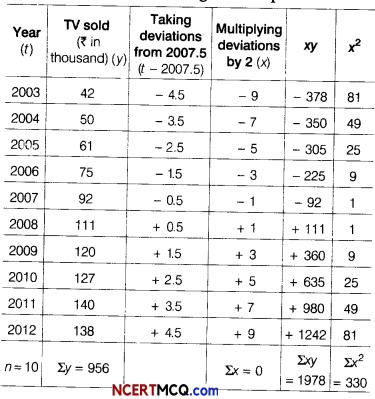
The linear equation would be of the form
y_t = a + bx
The two normal equations shall be
Σy = m + bΣx
Σxy = aΣx + bΣx²
Since, Σx = 0, a = \(\frac{\Sigma y}{n}=\frac{956}{10}\) = 95.6
and b = \(\frac{\Sigma x y}{\Sigma x^{2}}=\frac{1978}{330}\) = 5.994
Thus, the linear equation is y_t = 95.6 + 5.994 x
For 2014, x would be + 13
y₂₀₁₄ = 95.6+ 5.994(13)
= 95.6 + 77.92 = 173.52 thousand
Hence, the expected number of TV that would be sold in 2014 shall be ₹ 173520.

Question 8.
Consider the following hypothesis
H₀ : µ = 275
H₀ : µ ≠ 275
A sample of 60 provided a sample mean of 287.6. The population standard deviation is 15 and level of significance α = 0.05. Check the hypothesis test, given above using interval estimation.
Answer:
Given, µ₀ = 275, n = 60, x̄ = 287.6, σ = 15
and α = 005. So, Z_α/2 = Z_0.025 = 1.96
Confidence interval = x̄ ± Z_α/2. \(\frac{\sigma}{\sqrt{n}}\)
= 287.6 ± 1.96 × \(\frac{15}{\sqrt{60}}\)
= 287.6 ± 3.8
So, confidence interval is
(287.6 – 38,287.6 + 38) i.e. (2838,291.4).
Since, the hypothesized value of population mean µ₀ = 275 lies in the confidence interval (2838, 291.4), so H₀ cannot be rejected.

Question 9.
The present value of a perpetual income of ₹ R at the end of every month, the first being received at the end of 3 yr is ₹ 75000. Find the value of R, if money is worth 15% per annum compounded monthly [given, (1.0125)^-35 = 0.6474]
OR
A bond of face value of ₹ 1200 has a coupon rate 10% per annum paid semi-annually and matures in 6 yr. If the present value of the bond is ₹ 1560, find the yield to maturity.
Answer:
Clearly, it is the case of deferred perpetuity.
Present value (P) = ₹ 75000
Periodic payment = ₹ R
Rate of interest (r) = 15% = 0.15
Interest is compounded monthly, so we have
i = \(\frac{r}{12}=\frac{0.15}{12}\) = 0.0125
Since, the first payment is receivable at the end of 3 yr, the period of deferment (n) = 35.

∴ Approximate yield to maturity (YTM) = 0.0217
or 2% per half year or 4% per annum.

Question 10.
The demand functions for a commodity is given by p = 20 – 2x – x². Find the consumed surplus, when market demand is 3.
Answer:
It is given that x₀ = 3
On substituting x = 3 and p = p₀ in demand function
p = 20 – 2x – x², we get
p₀ = 20 – 6 – 9 = 5

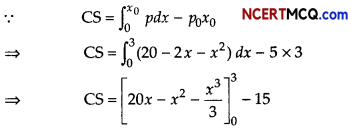
⇒ CS = (60 – 9 – 9) -15
⇒ CS = 27
Hence, consumer’s surplus is 27.

Section – C [16 Marks]

Question 11.
Mr. Taneja purchase a house of ₹ 4500000 with a down payment of ₹ 500000 and balance in EMI for 25 yr. If bank charges 6% per annum compounded monthly. Calculate the EMI. [given, (1.005)³⁰⁰ = 4.4650].
OR
Find the purchase price of a ₹ 20000 bond, redeemable at the end of 10 yr at 110 and paying annual dividends at 4%, if the yield rate is to be 5% effective.
[given, (1.05)^-10 = 0.6139]
Answer:
Cost of house = ₹ 4500000
Down payment = ₹ 500000
∴ Balance = ₹(4500000 – 500000) = ₹ 4000000
So, p = ₹ 4000000, i = \(\frac{6}{1200}\) = 0.005 and n = 25 × 12 = 300 months

Hence, EMI of Mr. Taneja is ₹ 25772.
Total interest paid = x(EMI) – P
= 300(25772) – 4000000
= 7731600 – 4000000
= 3731600
Hence, total interest paid is ₹ 3731600

Or

We have, n = Number of period = 10
and i yield rate = \(\frac{5}{100}\) = 0.05
R = Annual dividend
= 4% of face value
= ₹ \(\left(\frac{4}{100} \times 20000\right)\) = ₹ 800
The bond is redeemed at 110.
Therefore, the redemption price of the bond is 110% of its face value.
Thus, C = Redemption price
= ₹\(\left(20000 \times \frac{110}{100}\right)\) = ₹ 22000
Let V be the purchase price of the bond. Then,

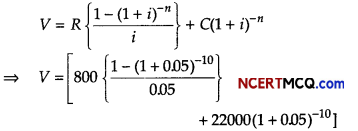
= [16000(1- (1.05)^-10] + 22000(1.05)^-10]
= [16000(1 – 0.6139) + 22000 (0.6139)]
= [16000(0.3861) +1350500]
= (617700 +1350500)
= ₹ 19683.40
∴ The purchase price of bond is 119683.40

Question 12.
A population grows at the rate of 10% per year. How long does it take for the population to double? Use differential equation for it.
Answer:
Let P₀ be the initial population and P be the population after t yr.

Question 13.
Diwakar invested ₹ 20000 in a mutual fund in year 2010. The value of mutual fund increased to ₹ 32000 in year 2015. Calculate the compound annual growth rate (CAGR) of his investment, [given, (1.6)^1/5 = 1.098]
Answer:
Given, the begining value of the investment = ₹20000
Fund value of the investment = ₹ 32000
Number of years = 5 yr

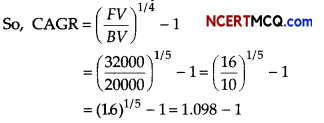
= 0.098 = (0.098 × 100)% = 9.8%
Hence, CAGR is 9.8%.

Case Based/Data Based

Question 14.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 h of machine time and 3 h of craftman’s time in its making, while a cricket bat takes 3 h of machine’s time and 1 h of craftman’s time. In a day, the factory has the availability of not more than 42 h of machine’s time and 24 h of craftman’s time.

(i) What number of rackets and bats must be made, if the factory is to work at full capacity?
(ii) If the profits on rackets and on bats is ₹ 20 and ₹ 10, respectively. Find the maximum profit of the factory, when it works at full capacity.
Answer:
Let the number of rackets and the number of cricket bats to be made in a day be x and y, respectively. Construct the following table.

Construct the following table.

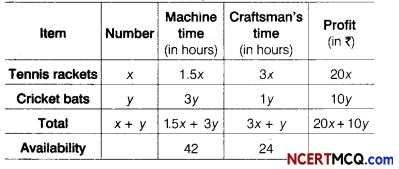
The machine time is not available for more than 42 h.
∴ 1.5x + 3y ≤ 42
The craftman’s time is not available for more than 24 h.
∴ 3x + y ≤ 24
The profit on rackets is ₹ 20 and on bats is ₹ 10.
∴ Maximum Z = 20x + 10y …(i)
Subject to constraints are,
15x + 3y ≤ 42 ……(ii)
3x + y ≤ 24
and x, y ≥ 0 ……. (iv)
Firstly draw the graph of the line
1.5x + 3y = 42

X	0	28
y	14	0

On putting (0, 0) in the inequality 1.5x + 3y ≤ 42, we have
1.5 × 0 + 3 × 0 ≤ 42
⇒ 0 ≤ 42 (which is true)
So, the half plane is towards the origin.
Since, x, y ≥ 0
So, the feasible region lies in the first quadrant. Secondly, draw the graph of the line
3x + y = 24

X	0	8
y	24	0

On putting (0, 0) in the inequality 3x + y ≤ 24, we have
3 × 0 + 0 ≤ 24 ⇒ 0 ≤ 24 (which is true)
So, the half plane is towards the origin.
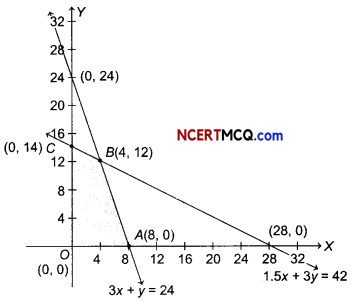
On solving equations 1.5x + 3y = 42 and 3x + y = 24, we get B (4,12).
∴ Feasible region is OABCO.
The comer points of the feasible region are
0 (0, 0), A (8, 0), B(4,12) and C (0,14).
The values of Z at these points are as follows.

Corner point	Value of Z = 20x + 10y
0(0, 0)	0
A(8, 0)	160
6(4, 12)	200 (Maximum)
C(0, 14)	140

Thus, the maximum profit of the factory, when it works to its full capacity is ₹ 200.
Hence, 4 tennis rackets and 12 cricket bats must be made, if the factory is to work at full capacity.