CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 11 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 11 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 11 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
Evaluate ∫\(\frac{d x}{x\left(x^{3}+8\right)}\)
Or
The supply function of a producer is given by p = \(\frac{2}{5}\)e^2x, where x denotes thousand units.
Find producer’s surplus when sales are 2000 units.
Answer:
Let I = ∫\(\frac{d x}{x\left(x^{3}+8\right)}\) = ∫\(\frac{x^{2}}{x^{3}\left(x^{3}+8\right)}\)dx
Now, put x³ + 8 = t

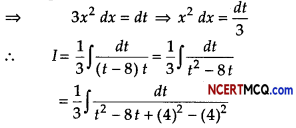
[adding and substracting by (4)² in denominator]

Or

Given, the supply function, p = \(\frac{2}{5}\)e^2x
When sales are 2000 units i.e. x₀ = 2, then we get
p₀ = \(\frac{2}{5}\)e⁴ [when x = 2 then p = latex]\frac{2}{5}[/latex]e⁴]

Question 2.
Find a linear trend to the following data by the least squares method,

Or
Find seasonal variations by ratio-to-trend method from the data given below.

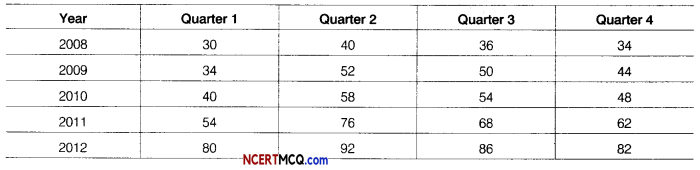
Answer:
Here, n = 5 is odd.
Hence, middle year i.e. 1989 taken as origin.

We construct the table as

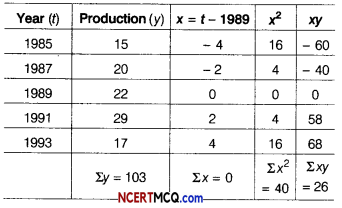
Let trend line of y (production) on x be
y_t = a + bx (origin 1989) ………(i)

The normal equation for estimating a and b in Eq. (i) are Σy = na + b Σx
⇒ 103 = 5a + b × 0
⇒ 5a = 103 ⇒ a = \(\frac{103}{5}\) = 20.6
and Σxy = aΣx + bΣx²
26 = a x O + b x 40
b = \(\frac{26}{40}\) = 0.65

The linear trend
y_t = a + bx
y_t = 20.6 + 0.65x

Or

For determining seasonal variation by ratio-to-trend method, first we will determine the trend of yearly data and then convert it to quarterly data.
Table for calculating trend values

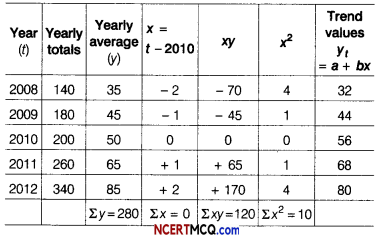
The equation of the straight line trend is y_t = a + bx.
Since, Σx = 0, a = \(\frac{\Sigma y}{n}=\frac{280}{5}\) = 56
and b = \(\frac{\Sigma x y}{\Sigma x^{2}}=\frac{120}{10}\) = 12
Quarterly increment = \(\frac{12}{4}\) = 3.

Question 3.
What sum of money invested, now would establish a scholarship of ₹ 20000 to be awarded at the starting of each year to a deserving student, if money is worth 8% compounded annually?
Answer:
Since, the payments are made at the starting of each year forever, it is a perpetuity due. Periodic payment (R) = ₹ 20000 Interest is compounded annually, so i = 8% = 0.08
Present value (P) of a perpetuity due is given as, P= R(1 + \(\frac{1}{i}\)) ⇒ P = 20000(1 + \(\frac{1}{0.08}\))
⇒ P = 20000 × 13.5 = 270000

∴ Amount to be invested is ₹ 270000.

Question 4.
A desktop computer costing ₹ 60000 has a useful life of 18 yr. If annual depreciation is ₹ 3000, find its scrap value, using linear method.
Answer:
Given, original cost of desktop computer = ₹ 60000
Useful life = 18 yr
Annual depreciation = ₹ 3000
Let the scrap, value of the desktop computer be ₹ S. Then, using annual depreciation
= \(\frac{\text { Original cost }-\text { Scrap value }}{\text { Useful life in years }}\)
3000 = \(\frac{60000-S}{18}\)
⇒ 54000 = 60000 – S ⇒ S = 6000
Hence, the scrap value of desktop computer is ₹ 6000.

Question 5.
Consider the following hypothesis test.
H₀ : µ ≤ 30
H₁ : µ > 30
A sample of 45 provided a sample mean of 32.4. The population standard deviation is 6.
(i) Compute the value of the test statistic.
(ii) What is the p-value?
Answer:
Given, µ₀ = 30, n = 45, x̄ = 32.4, σ = 6 and α = 0.01
(i) Test statistics,

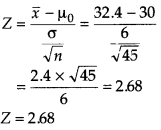
(ii) ∵ Z = 2.68 > 0
So, p-value of 2.68 = Area under the standard normal curve to the right of Z
= 1 – 0.9963 (using table) = 0.0037
∴ p-value = 0.0037

Question 6.
Find the maximum value of Z = 4x + 2y, subject to constraints are
2x + 3y ≤ 18, x + y ≥ 10 and x, y ≥ 0.
Answer:
The given LPP’s maximize Z = 4x + 2y
Subject to constraints are
2x + 3y ≤ 18, x + y ≥ 10 and x, y ≥ 0
The graph of the above LPP is

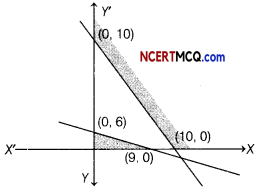
From the above graph, we see that for the feasible solutions there is no common area in the first quadrant. Hence, the objective function Z cannot be maximized.

Section – B [12 Marks]

Question 7.
You are given the following data about the life of two brands of bulbs.

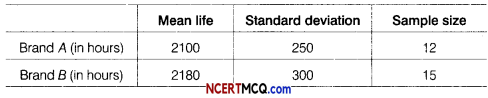
Do you think, there is a significant difference in the quality of the two brands of bulbs? (the table value of t for 25 degree of freedom at 5% level of significance is 1.708).
Answer:
Given, x̄₁ = 2100, s₁ = 250 and n₁ = 12,
x̄₂ = 2180, s₂ = 300 and n₂ = 15
Consider, null hypothesis : There is no significant difference in the quality of the two brands of bulbs.

Since, the computed value of t = 0739 is less than the table value of t = 1.708 [at 5% for 25 degree of freedom], we accept the null hypothesis.

Question 8.
The quarterly profits of a small scale industry (? in thousands) is as follows.

Calculate 4-quarterly moving averages, display these and the original figures graphically on the same graph sheet.
Answer:


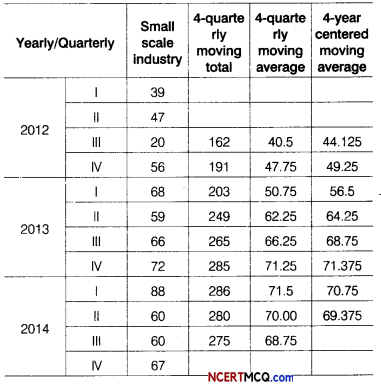
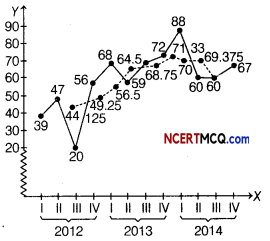
We draw the following graph from the above data.

A kink is shown near origin on the Y-axis to indicate that the scale on Y-axis starts with 20. The dark curve represents quarterly profits of a small scale industry and dotted curve represents 4-quarterly centered moving averages.

Question 9.
If the interest is compounded continuously at 6% per annum, how much worth ₹ 1000 will be 10 yr? (given, e^0.6 = 1.822)
Answer:
Let P be the principal amount at any time t and the rate of interest be r% per annum compounded continuously.

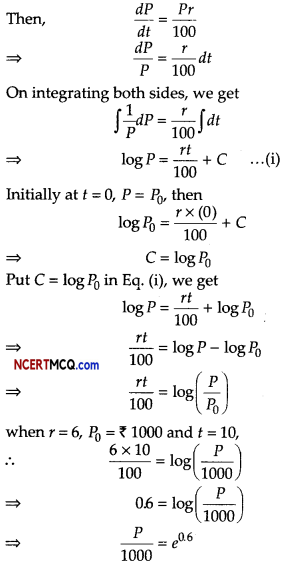
⇒ P = 1000 × 1.822
= 1822
Hence, in 10 yr, the worth of ₹ 1000 will become ₹ 1822.

Question 10.
The value of a car depreciates by 12.5% every year. By what percent will the value of the car decrease after 3 yr?
Or
A firm anticipates a capital expenditure of ₹ 80000 for a new equipment in 5 yr. How much should be deposited quarterly in sinking fund carrying 12% per annum compounded quarterly to provide for the purchase? [given (1.03)²⁰ = 1.8061]
Answer:
Let the present value of the car be ₹ P, then value of the car after 3 yr
= P(1 – i)ⁱ
= P(1 – \(\frac{12.5}{100}\))³
= P(1 – \(\frac{1}{8}\))³ = P\(\left(\frac{7}{8}\right)^{3}\)

Decrease in the value of the car after 3 yr
= P – P\(\left(\frac{7}{8}\right)^{3}\)
= P(1 – \(\frac{343}{512}\)) = \(\frac{169P}{512}\)

∴ Percentage decrease in the value of the car after 3 yr

Thus, ₹ 2977.29 deposited quarterly in a sinking fund.

Section – C [16 Marks]

Question 11.
The marginal cost function for a product is given by MC = \(\frac{5}{\sqrt{2 x+9}}\) and fixed cost ₹ 20 find the average cost for 10 units of output.
Answer:

It is given that x = 0 and C = 20
From Eq. (i) we get
20 = 5\(\sqrt{2 \times 0+9}\) + K
⇒ 20 = 15 + K
⇒ K = 5

Substituting K = 5 in Eq (i) we get
C = 5\(\sqrt{2 x+9}\) + 5
Now, AC = \(\frac{C}{x}\)

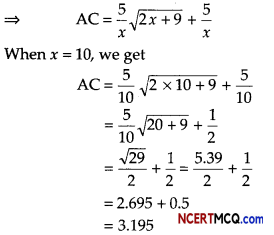
Hence, average cost for 10 units of outputs is ₹ 3.195

Question 12.
An aeroplane can carry a maximum of 200 passengers. A profit of ₹ 1000 is made on each executive class ticket and a profit of ₹ 600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
Or
A toy company manufactures two types of dolls A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is almost half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of type B by atmost 600 units. If the company makes profit of ₹ 12 and ₹ 16 per doll respectively, on dolls A and B, how many of each should be produced weekly in order to maximise the profit?
Answer:
Let x passengers travel by executive class and y passengers travel by economy class.

We construct the following table:

Class	Number of tickets	Profit (in ₹)
Executive	x	1000x
Economy	y	600y
Total	x+y	1000x+ 600y

So, our problem is to maximise
Z = 1000x + 600y …(i)
Subject to constraints,
x + y ≤ 200 …(ii)
x ≥ 20 …(iii)
y – 4x ≥ 0 ⇒ y ≥ 4x …(iv)
and x, y ≥ 0 ……….(v)

Firstly, draw the graph of the line x + y = 200

x	0	200
y	200	0

Putting (0, 0) in the inequality x + y ≤ 200, we have
0 + 0 ≤ 200 ⇒ 0 ≤ 200 (which is true)

So, the half plane is towards the origin. Secondly, draw the graph of the line y = 4x

x	0	20
y	0	80

Putting (10,0) in the inequality y ≥ 4x, we have
0 ≥ 4 x 10 ⇒ 0 ≥ 40 (which is false)

So, the half plane is towards Y-axis.
Thirdly, draw the graph of the line x = 20

Putting (0, 0) in the inequality x ≥ 20, we have 0 ≥ 20 (which is false)
So, the half plane is away from the origin. Since, x,y ≥ 0
So, the feasible region lies in the first quadrant.

On solving the equations, we get
A (20, 80), B(40, 160) and C (20, 180).
∴ Feasible region is ABCA

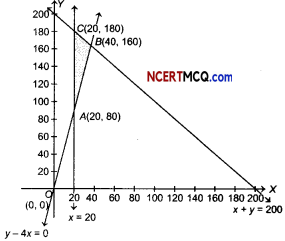
The corner points of the feasible region are A(20, 80), B(40,160) and C(20,180). The value of Z at these points are as follows:

Corner point	Value of Z = 1000x + 600y
.4(20, 80)	68000
8(40, 160)	136000 (Maximum)
C(20, 180)	128000

Thus, the maximum value of Z is 136000 at B(40, 160).

Thus, 40 tickets of executive class and 160 tickets of economy class should be sold to maximise the profit and the maximum profit is ₹ 136000.
Or
Let the company manufactures x dolls of type A and y dolls of type B, then
x,y ≥ 0 …(i)
x + y ≤ 1200 …(ii)
y ≤ x/2 ⇒ x – 2y ≥ 0 …(iii)
and x ≤ 3y + 600 ⇒ x -3y ≤ 600 …(iv)

Firstly, draw the graph of the line x + y = 1200

x	1200	0
y	0	1200

Putting (0, 0) in the inequality x + y ≤ 1200, we have
0 + 0 ≤ 1200 ⇒ 0 ≤ 1200 (which is true)

So, the half plane is towards the origin. Secondly, draw the graph of the line x – 2y = 0
Putting (200, 0) in the inequality x – 2y ≥ 0, we have
200 – 2 × 0 ≥ 0 ⇒ 200 ≥ 0 (which is true)

So, the half plane is towards the X-axis.

Thirdly draw the graph of the line x – 3y = 600

x	600	0
y	0	-200

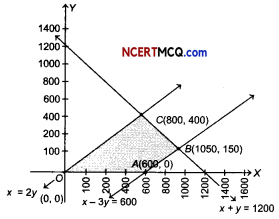
Putting (0, 0) in the inequality x – 3y≤ 600, we have
0 – 3 x 0 ≤ 600 ⇒ 0 ≤ 600 (which is true)

So, the half plane is towards the origin.
Since, x,y ≥ 0, so the feasible region lies in the first quadrant.

The point of intersection of lines x – 3y = 600 and x + y = 1200 is B(1050,150), of lines x = 2 y and x + y = 1200 is C (800,400).
Let Z be the total profit, then Z = 12 x +16y

Feasible region is OABCO.
The comer points of the feasible region are A (600,0), B(1050,150) and C(800,400).

The values of Z at these points are as follows.

Corner point	Value of Z = 12x + 16y
4(600, 0)	7200
fi{1050, 150)	15000
C(800, 400)	16000 (Maximum)

The maximum value of Z is 16000 at C(800,400).

Thus, 800 and 400 dolls of types A and type B should be produced respectively to get the maximum profit of ₹ 16000.

Question 13.
Face value of bond is 1 1000, coupon rate 4.25% per annum paid semi-annually and matures in 10 yr. If present value of bond is ₹ 918.23. What is the yield to maturity.
Answer:
Given, F = ₹ 1000, r = 4.25%
and i = \(\frac{4.25}{2}\)% = \(\frac{4.25}{200}\) (semi-annually)
So, C = ₹ 1000 × \(\frac{4.25}{200}\) = ₹ 21.25 200
N = 10 × 2 = 20 yr and PV = ₹ 918.23

Approximate Yield to Maturity (YTM)

Approximate YTM = 2.64% (semi-annually)
= 5.28% per annum

Hence, yield to maturity is 5.28 per annum.

Case Based/Data Based

Question 14.
A loan is the leading of money by one or more individual, organisations or other entities to other individuals, organisations etc. The recepient incurs a debt and is usually liable to pay interest on that debt untill it is repaid as well as to repay the principle amount borrowed.

A loan of ₹ 400000 at the interest rate of 6.75% per annum compounded monthly is to be amortized by equal payment at the end of each month for 10 yr, find
(i) the size of each monthly payment
(ii) the principal outstanding at the beginning of 61st month. [given (1.005625)¹²⁰ = 1.9603 and (1.005625)⁶⁰ =1.4001]
Answer:
Given, P = ₹ 400000, n = 12 × 10 = 120 675
and i = \(\frac{6.75}{1200}\) = 0.005625

(i) ∴ Size of monthly payment (EMI)

Hence, monthly payment is ₹ 4593

(ii) We know that principal outstanding at beginning of kth period
= \(\frac{\operatorname{EMI}\left[(1+i)^{n-k+1}-1\right]}{i(1+i)^{n-k+1}}\)
So, principal outstanding at beginning of 61st month

Hence, principal outstanding at beginning of 61st month is ₹ 233336.89