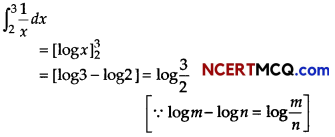Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 2 with Solutions
Maximum Marks : 40
Time : 2 Hours
Instructions:
- The question paper is divided into 3 sections-A, B and C
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.
Section – A [12 Marks]
Question 1.
Evaluate ∫ log x dx.
Or
The marginal cost function of manufacturing x units of a commodity is 6 + 10x – 6x2. The total cost of producing one unit of commodity is ₹ 12. Find the total cost function.
Answer:
Let I = ∫ log dx
I = ∫log x ∙ 1 dx
On applying integration by parts, we get
I = log x ∫1 dx – ∫[\(\frac{d}{d x}\) log x ∫1 dx]dx
I = log x ∙ x – ∫\(\frac{1}{x}\) ∙ x dx + C
I = x log x – ∫1 dx + C
I = x log x – x + C
Or
We have, MC = 6 + 10x – 6x2
∴ \(\frac{d C}{d x}\) = MC
On integrating both sides, we get
∫dC = ∫(6 + 10x – 6x2)dx
C = 6x + 5x2 – 2×33 + K ……. (i)
It is given that the cost of producing one unit of the commodity is ₹ 12, i.e. x = 1 and C = 12
Putting x = 1 and C = 12 in Eq. (i), we get
12 = 6 + 5 – 2 + K
K = 3
On substituting the value of K in Eq. (i), we get
C = 6x + 5x2 – 2x3 + 3
![]()
Question 2.
Sanchit borrowed a home loan amount of ₹ 5000000 from a bank at an interest rate of 12% per annum for 30 yr. Find the equated monthly installment amount, Sanchit has to pay to the bank, [given (1.01) -360 = 0.02781].
Or
A bike costing ₹ 55000 has a useful life of 15 yr. If annual depreciation is ₹ 3000.
Find its scrap value, using linear method.
Answer:
Given, P = ₹ 5000000, i = \(\frac{12}{1200}\) = 0.01
and n = 12 × 30 = 360
Let E be the equated monthly installment Sanchit has to pay to the bank.
∴ E = \(\frac{P \times i}{1-(1+i)^{-n}}\)
Here, E = \(\frac{5000000 \times 0.01}{1-(1+0.01)^{-360}}\)
= \(\frac{50000}{1-(1.01)^{-360}}\) = \(\frac{50000}{1-0.02781}\)
= \(\frac{50000}{0.97219}\) = 51430.27
Hence, Sanchit EMI is ₹ 51430.27
Or
Given, cost of bike = ₹ 55000,
Useful life = 15 yr
and Annual depreciation = ₹ 3000
Let scrap value of bike is ₹ S.
Then, annual depreciation = \(\frac{\text { Original cost }-\text { Scrap value }}{\text { Useful life in years }}\)
⇒ 3000 = \(\frac{55000-S}{15}\)
⇒ 45000 = 55000 – S
⇒ S = 55000 – 45000 = 10000
Hence, scrap value is ₹ 10000
![]()
Question 3.
Find the present value of a perpetuity of ₹ 5280 payable at the beginning of each year, if money is worth 8% effective.
Answer:
Given, R = ₹ 5280, i = \(\frac{8}{100}\) = 0.08
and let P be the present value of the given perpetuity.
∴ P = R + \(\frac{R}{i}\)
= 5280 + \(\frac{5280}{0.08}\)
= 5280 + 66000
= 71280
Hence, present value of the given perpetuity is ₹ 71280.
Question 4.
A sampling distribution of the sample means X̄ is formed from a population with mean weight µ = 55 kg and standard deviation σ = 8 kg. What is expected value and standard deviation of X̄, if sample size is 49?
Answer:
We have,
µ = 55 kg
∴ E(X̄) = 55 kg
Standard deviation of X̄ = D(X̄) = \(\frac{\sigma}{\sqrt{n}}\)
= \(\frac{8}{\sqrt{49}}\) = \(\frac{8}{7}\) = 1.142 kg
![]()
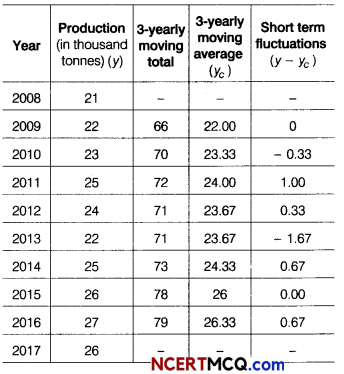
Question 5.
Using 3-yearly moving averages, compute the trend values and short term fluctuations for the following data.

Answer:
Computation of trend value
Question 6.
Determine the maximum value of Z = 11x + 7y, subject to the constraints are 2x + y ≤ 6, x ≤ 2 and x, y ≥ 0.
Answer:
We have,
Maximise Z = 11 x + 7y …….. (i)
Subject to the constraints,
2x + y ≤ 6 ……. (ii)
x ≤ 2 ……. (iii)
and x, y ≥ 0 ……. (iv)
We see that, the feasible region as shaded determined by the system of constraints (ii) to (iv) is OABC and is bounded. So, now we shall use comer point method to determine the maximum value of Z.
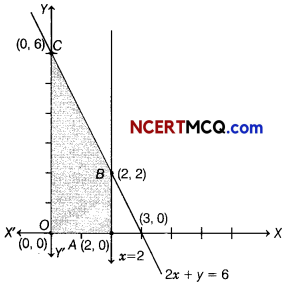
| Corner points | Value of Z = 11x + 7y |
| 0(0, 0) | Z = 11(0) + 7(0) = 0 |
| A(2, 0) | Z = 11(2) + 7(0) = 22 |
| B(2, 2) | Z = 11(2) + 7(2) = 36 |
| C(0, 6) | Z = 11(0) + 7(6) = 42 (Maximum) |
Hence, the maximum value of Z is 42 at C(0, 6).
![]()
Section -B [12 Marks]
Question 7.
Two batches of the same product are tested for their mean life. Assuming that, the lives of the product follow a normal distribution with an unknown variance, test the hypothesis that the mean life is the same for both the branches, given the following information.

[given, t16 (0.05) = 2.120]
Or
The Educational Testing Service conducted a study to investigate difference between the scores of male and female students on the Scholastic Aptitude Test. The study identified a random sample of 562 female and 852 male students, who had achieved the same high score on the mathematics portion of the test. That is, female and male students were viewed as having similarly high abilities in mathematics. The verbal scores for the two samples are as given
Female students, x̄1 = 557 and s1 = 83
Male students, x̄2 = 545 and s2 = 78
Do the data support the conclusion that given a population of female students and a population of male students with similarly high mathematics abilities, the female students will have a significantly higher verbal ability? Test at a 5% level of significance. What is your conclusion?
Answer:
Given, n1 = 10, n2 = 8, x̄1 = 750, x̄2 = 820,
s1 = ₹ 12 and s2 = ₹ 14
Consider, Null hypothesis H0 : Mean life is same for both the batches.
Alternate hypothesis H1 : Two batches have different mean lives.
Test statistics,

Since, calculated value |t| = 10.763 > tabulated value
t16(0.05) = 2.120
So, rejected the null hypothesis at 5% level of significance.
Hence, the mean life for both the batches is not the same.
Or
We have, x̄1 = 557, x̄2 = 545, s1 = 83, s2 = 78,
n1 = 562 and n2 = 852
Consider, the null hypothesis be that there is no significant difference between male and female verbal ability,
H0: µ1 – µ2 > 0 and H1: µ1 – µ2 < 0
Test statistics,

Here, the computed value of Z is greater than the table value of Z i.e. 1.96. So, reject the null hypothesis. Hence, there is a significant difference between the male and female verbal ability or female students have higher verbal ability.
![]()
Question 8.
The production of a soft drink company in thousand of litres during each month of a year is as follows

Calculate the 5-monthly moving average and show these moving averages on a graph.
Answer:
According to the question,
| Months | Production (in thousand litre) |
| Jan | 1.2 |
| Feb | 0,8 |
| Mar | 1.4 |
| Apr | 1.6 |
| May | 1.8 |
| June | 2.4 |
| July | 2.6 |
| Aug | 3.0 |
| Sept | 3.6 |
| Oct | 2.8 |
| Nov | 1.9 |
| Dec | 3.4 |
Let the 5-monthly moving average of the Jan-Dec production is m.
So,

On the basis of above data, we can draw the following graph
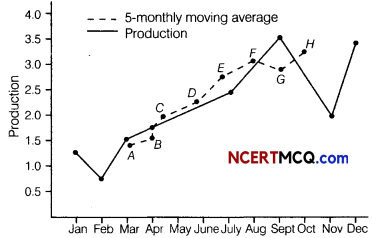
Question 9.
Mr. Amit invested ₹ 10000 in a mutual fund and the value of investment at the time of redemption was ₹ 25000. If compound annual growth rate (CAGR) for this investment is 9.15%. Calculate the time period for which the amount was invested? [given, log(2.5) = 0.3979 and log(1.0915) = 0.0380]
Answer:
Given, BV = ₹ 10000, EV = ₹ 25000 and CAGR = 9.15%
We know that

Taking log on both sides, we get
\(\frac{1}{n}\) log(2.5) = log(1.0915)
⇒ n = \(\frac{\log (2.5)}{\log (1.0915)}=\frac{0.3979}{0.0380}\)
⇒ n = 10.47 = 10.5 yr
![]()
Question 10.
The demand function for a commodity is p = 22 – x – x2. Find the consumer’s surplus at equilibrium price p0 = 10.
Answer:
Given, the demand function is p = 22 – x – x2
at the equilibrium price p0 = 10
We have,
10 = 22 – x0 – x20
⇒ x20 + x0 – 12 = 0
⇒ x20 + 4x0 – 3x0 – 12 = 0
⇒ x0(x0 + 4) – 3(x0 + 4) = 0
⇒ (x0 – 3) (x0 + 4) = 0
⇒ x0 = 3 or x0 = – 4
Since, x0 ≠ – 4
⇒ x0 = 3
∴ Consumer’s surplus (CS) at p0 = 10
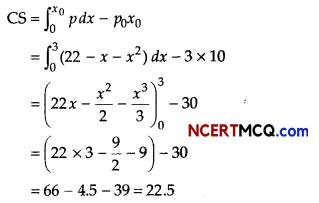
Hence, consumer’s surplus is 22.5.
Section – C [16 Marks]
Question 11.
An aeroplane can carry a maximum of 200 passengers. A profit of ₹ 1000 is made on each executive class ticket and a profit of ₹ 600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
Or
Determine graphically the minimum value of the objective function Z = – 50x + 20y, subject to constraints are 2x – y ≥ – 5, 3x + y ≥ 3, 2x – 3y ≤ 12 and x, y ≥ 0.
Answer:
Let x passengers travel by executive class and y passengers travel by economy class.
We construct the following table
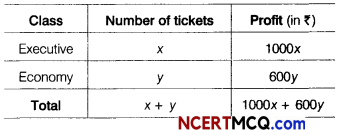
So, our problem is to maximise
Z = 1000x + 600y ………. (i)
Subject to constraints,
x + y ≤ 200 x ≥ 20
y – 4x ≥ 0 or y ≥ 4x
and x, y ≥ 0
Table for line x + y = 200 is
| X | 0 | 200 |
| y | 200 | 0 |
So, line passes through,the points (0, 200) and (200,0).
On putting (0, 0) in the inequality x + y ≤ 200, we get
0 + 0 ≤ 200 ⇒ 0 ≤ 200, which is true.
So, the half plane is towards the origin.
Table for line y = 4x is
| X | 0 | 20 |
| y | 0 | 80 |
So, line passes through the points (0, 0) and (20, 80).
On putting (10, 0) in the inequality y ≥ 4x, we get
0 ≥ 4 x 10 ⇒ 0 ≥ 40, which is not true.
So, the half plane is towards Y-axis.
Now, draw the graph of the line x = 20.
On putting (0,0) in the inequality x ≥ 20,
we get
0 ≥ 20, which is not true.
So, the half plane is away from the origin.
Also, x, y ≥ 0, so the region lies in the I quadrant.
On solving Eqs. (ii), (iii) and (iv), we get
A(20,80), B(40,160) and C (20,180).
∴ Feasible region is ABCA
The comer points of the feasible region are
A(20,80), 6(40,160) and C(20,180).
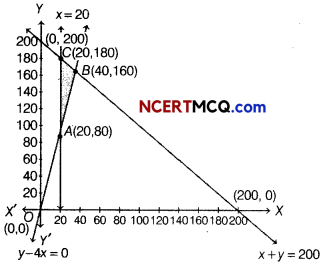
The value of Z at the corner points are given below
| Corner points | Value of Z = 1000x + 500 |
| A(20, 80) | Z = 1000 x 20 + 600 x 80 = 68000 |
| B(40,160) | Z = 1000 x 40 + 600×160 = 136000 (Maximum) |
| C(20,180) | Z = 1000×20+ 600×180 = 128000 |
Thus, the maximum value of Z is 136000 at B(40,160).
Thus, 40 tickets of executive class and 160 tickets of economy class should be sold to maximise the profit and the maximum profit is if 136000.
Or
Given, objective function is
Minimise Z = – 50 x + 20y
Subject to constraints,
2x – y ≥ – 5 … (i)
3x + y ≥ 3 ……(ii)
2x – 3y ≤ 12 ……. (iii)
and x, y ≥ 0 …(iv)
Table for line 2 x – y = – 5 is
| X | -5/2 | 0 |
| y | 0 | 5 |
So, the line passes through the points (\(\frac{-5}{2}\), 0) and (0, 5).
On putting (0, 0) in the inequality 2x – y ≥ – 5, we get
0 – 0 ≥ – 5
⇒ 0 ≥ – 5, which is true.
So, the half plane is towards the origin.
Table for line 3x + y = 3 is
| X | 0 | 1 |
| y | 3 | 0 |
So, the line passes through the points (0, 3) and (1, 0).
On putting (0, 0) in the inequality 3x + y ≥ 3, we get
0 + 0 ≥ 3
⇒ 0 ≥ 3, which is not true.
So, the half plane is away from the origin.
Table for line 2x – 3y = 12 is
| X | 0 | 6 |
| y | -4 | o |
On putting (0, 0) in the inequality 2 x – 3y ≤ 12,
we get Z
0 – 0 ≤ 12
⇒ 0 ≤ 12, which is time.
So, the half plane is towards the origin.
Also, x ≥ 0 and y ≥ 0, so the region lies in the I quadrant.
On drawing the graph of each linear equation, we get the following graph. In I quadrant, these equations has no intersection point.
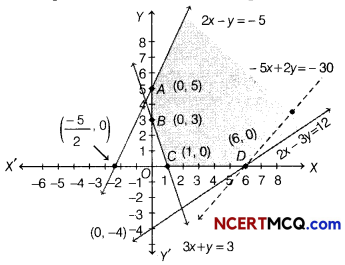
Thus, we get the common shaded region ABCD, which gives the feasible region and it is unbounded. The comer points of feasible region are A(0, 5), B(0, 3), C(1, 0) and D(6, 0).
The value of Z at comer points are given below
| Corner points | Value of Z = – 50x + 20y |
| 4(0, 5) | Z = – 50(0)+ 20(5) = 100 |
| 6(0 3) | Z = – 50(0) + 20(3) = 60 |
| C(1. 0) | Z = – 50(1) + 20(0) = – 50 |
| D( 6, 0) | Z = – 50(6) + 20(0) = – 300 |
Here, feasible region is unbounded, so the minimum and maximum value may or may not be exist.
Now, we draw a dotted line of inequation
– 50x + 20y < – 300
or – 5x + 2y < – 30
Here, we see that half plane determined by – 5x + 2y < – 30 has a point in common with the feasible region.
Hence, no minimum value exists.
![]()
Question 12.
A person borrows ₹ 68962 on the condition that the will repay the money with compound interest at 5% per annum in 4 equal annual installments, the first one being payable at the end of the first year. Find the value of each installment.
[given (1.05)-4 = 0.8227]
Answer:
According to the question, the borrow amount (principal amount = P) is ₹ 68962 .
Rate of interest, i = 5% per annum or \(\frac{5}{100}\)
Total number of installments (n) = 4
Let the value of each installment is a.
We know that
P = \(\frac{a}{i}\) [1 – (1 + i)-n] …….. (i)

0.1773
a = 19447.82
So, the value of each installment is ₹ 1944732.
Question 13.
A company has issued a bond having face value of ₹ 120000, carrying an annual dividend rate of 8% and maturing in 15 yr. If the prevailing market rate of interest is 10% and the bond is redeemed at par, find the bond value, [given (1.1)-15 = 0.2394)]
Answer:
Given, face value (F) = ₹ 120000
n = 15
and i = \(\frac{10}{100}\) = 0.1
Here, R = Annual dividend
= 8% of face value
= \(\frac{8}{100}\) × 120000 = ₹ 9600
If a bond is redeemed at par, then C = F
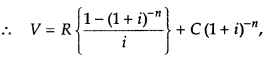
where C is redemption price or maturity value.
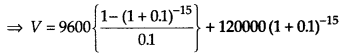
= 96000[1 – (1.1)-15] + 120000(L1)-15
= 96000(1 – 0.2394) + 120000 × 0.2394
= 96000 × 0.7606 + 28728
= 73017.6 + 28728
= ₹ 101745.6
![]()
Case Based/Data Based
Question 14.
In Angrish Academy School, class teacher of Xllth class teaches the topic of definite integration.

If f(x) is the continuous function, integral of f(x) over the interval [a, b] is denoted by
![]()
![]()
On the basis of above information, answer the following questions.
(i)
![]()
Answer:
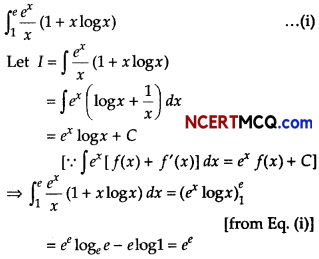
(ii)
![]()
Answer: