CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 3 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
Evaluate ∫\(\frac{(2 x-5) e^{2 x}}{(2 x-3)^{3}}\) dx
Or
Evaluate ∫\(\frac{\left(x^{3}+8\right)(x-1)}{x^{2}-2 x+4}\) dx
Answer:

Question 2.
A random sample of 12 families in one city showed an average weekly food expenditure of ₹ 1380 with a standard deviation of ₹ 100 and a random sample of 15 families in another city showed an average weekly food expenditure of ₹ 1320 with a standard deviation of ₹ 120. Test, whether the difference between the two means is significant at a level of significance of 0.01.
Or
A population consisting of 6 units 1, 2, 3, 4, 5 and 9. Find 95% confidence interval for estimating the population mean.
Answer:
Given, n₁ = 12, n₂ = 15, x̄₁ = 1380, x̄₂ = 1320, s₁ = ₹ 100 and s₂ = ₹ 120

Consider, the null hypothesis that there is no significant difference in the mean expenditure of the families in the two cities.
We know that test statistics

Here, degree of freedom v =12 +15 – 2 = 25 From v = 25, test statistics, t_0.01 = 2.485. Here, the calculated value t is less than the table value. Therefore, the null hypothesis is accepted. Hence, the difference between the two means is not significant.
Or
Mean, x̄ = \(\frac{24}{6}\) = 4
Now, S² = \(\frac{1}{n – 1}\)Σ(x_i – x̄)²
= \(\frac{1}{5}\)[(-3)² + (-2)² + (-1)² + 0² + (1)² + (5)²]
= \(\frac{1}{5}\) [9 + 4 + 1 + 1 + 25] = \(\frac{1}{5}\) × 40 = 8
∴S = √8 = 2√1
∴ Point estimate for a is 2√2.
∴ 95% confidence interval is

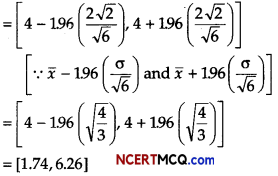
Question 3.
A man borrows ₹ 30000 at 12% per annum compound interest from a bank and promises to pay off the loans in 20 annual installments beginning at the end of first year. What is the annual payment necessary? [given (1.12)²⁰ = 9.638]
Answer:
Let ₹ R be the annual payment and ₹ P be the present worth.
Given, P = ₹ 30000, i = \(\frac{12}{100}\) = 0.12 and n = 20

We know that,

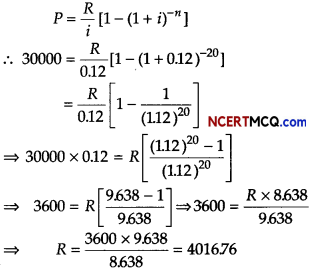
Hence, the annual payment should be ₹ 4016.76.

Question 4.
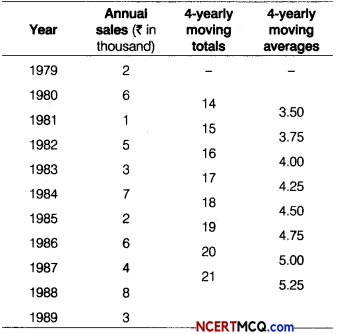
Construct 4-yearly moving averages from the following data

Answer:
Computation of 4-yearly moving averages

Question 5.
The value of a machine purchased 2 yr ago, depreciates at the annual rate of 8%. If its present value is ₹ 85100, find its value, when it was purchased.
Answer:
∴ Present value = Value of 2 yr ago × (1 – i)²
⇒ 85100 = Value of 2 yr ago (1 – 0.08 )²
⇒ 85100 = Value of 2 yr ago × (0.92 )²
⇒ Value of 2 yr ago = \(\frac{85100}{(0.92)^{2}}=\frac{85100}{0.8464}\)
= ₹ 100543.4783

Question 6.
Two tailors A and B, earn ₹ 300 and ₹ 400 per day respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day. To find how many days should each of them work and if it is desired to produce at least 60 shirts and 32 pairs of trousers at a minimum labour cost, formulate this as an LPP.
Answer:
The given data can be summarised as follows:

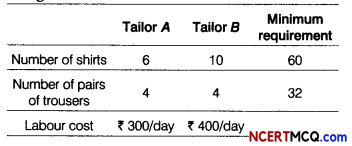
Let tailor A and tailor B works for x days and y days, respectively.
Then, x ≥ 0, y ≥ 0
∵ Minimum number of shirts = 60
∴ 6x + 10y ≥60 => 3x + 5y ≥ 30

Minimum number of trousers = 32
∴ 4x + 4y ≥ 32
⇒ x + y ≥ 8

Let Z be the total labour cost.
Then, Z = 300x + 400y
So, the given LPP reduces to Z = 300x + 400y
x ≥ 0, y ≥ 0, 3x + 5y ≥ 30 and x + y ≥ 8

Section – B [12 Marks]

Question 7.
If the marginal revenue functions of a commodity is MR = 9 – 6x² + 2x, find the total revenue and the corresponding demand functions.
Or
The marginal cost of a product is a constant multiple of number of units (x) produced. Find the total cost and the average cost function, if the fixed costs is ₹ 2000 and cost of producing 20 units is ₹ 3000.
Answer:
We have, MR = 9 – 6x² + 2x
∴ \(\frac{d R}{d x}\) = MR
dR = MRdx
⇒ ∫dR = ∫MRdx [integrating both sides]
⇒ ∫dR = ∫(9 – 6x² + 2x)dx
⇒ R = 9x – 2x³ + x² + K ………..(i)

When, x = 0, we have R = 0, then K = 0
∵ R = 9x – 2x³ + x² [from Eq. (i)]
If p is the price per emit when x units are sold, then
⇒ p = \(\frac{R}{x}\)
⇒ p = \(\frac{9 x-2 x^{3}+x^{2}}{x}\)
p = 9 – 2x² + x
Hence, demand functions is p = 9 – 2x² + x.
Or
Let MC = kx, where k is a constant.
We know that,
dC = (MC)dx
∫ dC = ∫(kx)dx
⇒ ∫dC = ∫(kx)dx [integrating both sides]
C = k ∫xdx = k\(\frac{x^{2}}{2}\) + k

where, k is a constant of integration.
Since, C = 2000, when x = 0
∴ k = 2000
Also, given that, C = 3000, when x = 20
3000 = k\(\frac{400}{2}\) + 2000
⇒ 200k = 1000 ⇒ k = 5
Thus, C = \(\frac{5 x^{2}}{2}\) + 2000 and AC = \(\frac{5 x}{2}+\frac{2000}{x}\) [∵AC = \(\frac{C}{x}\)]

Question 8.
Samples of sales in similar shops in towns A and B regarding a new product yielded the following information.

Is there any evidence of difference in sales in the two towns? [given t₁₈ (0.05) = 2.10]
Answer:
Consider, null hypothesis H₀ : There is no significant difference in sales in similar shops in towns A and B, and alternate hypothesis H₁ : Sales in similar shops in towns A and B are not same.

Test statistics
t = \(\frac{\bar{x}_{1}-\bar{x}_{2}}{S} \times \sqrt{\frac{n_{1} n_{2}}{n_{1}+n_{2}}}\)
where S = \(\frac{n_{1} s_{1}^{2}+n_{2} s_{2}^{2}}{n_{1}+n_{2}-2}\)

Given, n₁ = 11, x̄ = 3.45, Σx_i = 38, Σx_i² = 228
n₂ = 11, ȳ = 4.44, Σy_i = 40, Σy_i² = 222

Here, degree of freedom,
v = n₁ + n₂ – 2 = 11 + 9 – 2 = 18

Since, calculated value of t(- 0.784) is less than tabulated value of t[t₁₈(0.05) = 2.10], therefore the null hypothesis is accepted a 5% level of significance. Hence, there is no difference is sales in two towns.

Question 9.
A firm sets aside a sum of ₹ 10000 annually for 15 yr to pay-off a debenture issue of ₹ 220000. If the fund accumulates at 6% per annum, find the surplus after the full redemption of the debenture issue, [given (1.06)¹⁵ = 2.3965]
Answer:
Given, payment(R)= 10000
Number of periods(n) =15
Rate of interest (i) =6% = 0.06

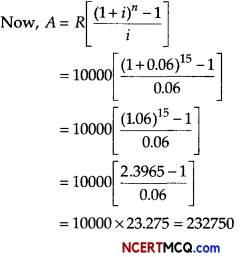
∴ The surplus = ₹(23.275 – 220000) = ₹ 12750

Question 10.
Fit a straight line trend by the method of least squares to the following data on sales (₹ in lakh) for the period 2005-2012.

Also,
(i) calculate the trend values from 2005 to 2012.
(ii) what will be predicted sales for 2015, assuming that the same rate of change continues?
Answer:
Here, n = 8(even)
So, origin is mean of two middle years
i.e. \(\frac{2008+2009}{2}\) = 2008.5

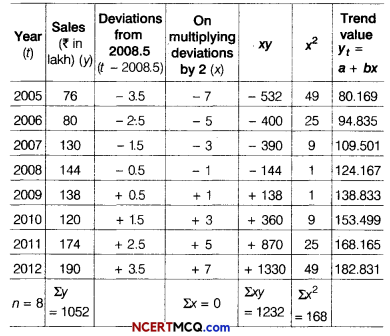
Since, Σx = 0,
a = \(\frac{\Sigma y}{n}=\frac{1052}{8}\) = 131.5 and
b = \(\frac{\Sigma x y}{\Sigma x^{2}}=\frac{1232}{168}\) = 7.333
Hence, y_t = 131.5 + 7.333x
For the year 2015, x would be 13, therefore
y₂₀₁₅ =131.5+7.333(13)
= 131.5 + 95.329 = 226.829 = ₹ 226.829

Section – C [16 Marks]

Question 11.
Amit has taken a loan of ₹ 1000000 with interest rate 11% per annum for the period of 15 yr. Calculate (reducing) EMI for the above data, [given (1.0091)¹⁸⁰ = 5.1068]
Answer:
We have, loan amount(P) = ₹ 1000000
Interest rate = 11% (per annum)
∴ Monthly Interest Rate
i = \(\frac{11 \%}{12 \text { months }}\)
= \(\frac{0.11}{12}\) = 0.0091

Loan period (n) =15 yr
=15 × 12 = 180 months

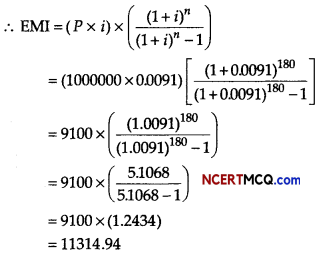
Hence, EMI is ₹ 11314.94 (approximately).

Question 12.
A bond has a face value of ₹ 10000 and matures in 15 yr at par. The nominal interest is 7%. What is the price of bond that will yield on effective interest of 8%. [given, (1.08)^-15 = 0.3152]
Answer:
We have,
F= Face value = ₹ 10000
n = Number of periods = 15
I = Annual yield rate = = 008
R = Annual dividend = ₹ (7 × 1oooo) = ₹ 700
C = Maturity value = Face value = ₹ 10000

Let V be the purchase price of the bond, then
V= R\(\left(\frac{1-(1+i)^{-n}}{i}\right)\) + C(1+ i)^-n
V=700\(\left(\frac{1-(1+0.08)^{-15}}{0.08}\right)\) + 10000(1 + 0.08)^-15
V = \(\frac{700}{0.08}\)(1 – (108)^-15) + 10000 (1.08)^-15
V = \(\frac{70000}{8}\)(1 – 0.3152) + 10000(0.3152)
⇒ V = \(\frac{70000}{8}\)(0.6848) + 3152
V = 5992 + 3152 = 9114
Hence, the purchase price of bond is ₹ 9144

Question 13.
A decorative item dealer deals in two items A and B. He has ₹ 15000 to invest and a space to store at the most 80 pieces. Item A costs him ₹ 300 and item B costs him ₹ 150. He can sell items A and B at respective, profits of ₹ 50 and ₹ 28. Assuming, he can sell all he buys, formulate the linear programming problem in order to maximise his profit and solve it graphically.
Or
An aeroplane can carry a maximum of 200 passengers. A profit of ₹ m is made on each executive class ticket and a profit of ₹ n is made on each economy class ticket, where m and nare obtained on multiplying first term and common ratio by 100 of the geometric series 10,60,360,… times. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine, how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
Answer:
Let the number of items of the type A and Bbe x and y, respectively. Then, the required LPP is Maximise Z = 50x + 28 y Subject to the constraints,
x + y ≤ 80, 300x + 150y ≤ 15000
or
2x + y ≤ 100 and x, y ≥ 0

Let us consider the inequalities as equations, we get
x + y = 80 ……(i)
2x + y = 100 ……..(ii)

Table for line x + y = 80 is:

x	0	80
y	80	0

So, it passes through the points (0, 80) and (80, 0).
On putting (0, 0) in the inequality x + y ≤ 80, we get
0+0 ≤ 80
⇒ 0 ≤ 80 (which is true)
So, the half plane is towards the origin.

Table for line 2x + y = 100

x	0	50
y	100	0

So, it passes through the points (0,100) and (50, 0)
On putting (0, 0) in the inequality 2x + y ≤ 100,

we get
2 (0) + 0 ≤ 100
⇒ 0 ≤ 100 (which is true)

So, the half plane is towards the origin.
On solving Eqs. (i) and (ii), we get
x = 20 and y = 60

So, the point of intersection is (20, 60).

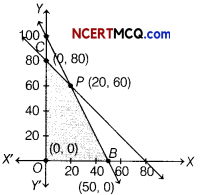
The feasible region is OBPC whose comer points are 0(0,0), B(50,0), P(20,60) and C(0, 80).

Corner Points	Value of Z = 50x + 28y
0(0,0)	0
C (0,80)	2240
P(20, 60)	2680 (Maximum)
B (50, 0)	2500

From the above table, the maximum value of Z is 2680 at P(20, 60), i.e. when 20 items of type A and 60 items of type B are purchased and sold. He get maximum profit.
Or
Given geometric series is 10, 60, 360,…
Here, first term (a) = 10 and common ratio
r = \(\frac{60}{10}\) = 6

According to the given condition,
m = a × 100 and n = r × 100
∴ m = 10 × 100 and n = 6 × 100
⇒ m = 1000 and n = 600

Let x passengers travel by executive class and y passengers travel by economy class.
We construct the following table:

Class	Number of tickets	Porfit (in ₹)
Executive	x	1000x
Economy	y	600y
Total	x + y	1000x + 600y

So, our problem is to maximise
Z = 1000x + 600y …(i)
subject to constraints
x + y ≤ 200 …(ii)
x ≥ 20 …(iii)
y – 4x ≥ 0 or y ≥ 4x …(iv)
and x ≥ 0, y ≥ 0 …(v)

Table for line x + y = 200 is

x	0	200
y	200	0

So, line passes through the points (0,200) and (200,0).
On putting (0, 0) in the inequality x + y < 200, we get 0 + 0 ≤ 200 ⇒0 ≤ 200, which is true.

So, the half plane is towards the origin. Table for line y = Ax is

x	0	20
y	0	80

So, line passes through the points (0,0) and (20,80). On putting (10, 0) in the inequality y > Ax, we get
0 ≥ 4 × 10 ⇒ 0 ≥ 40, which is not true.
So, the half plane is towards Y-axis.

Now, draw the graph of the line x = 20.
On putting (0, 0) in the inequality x ≥ 20, we get
0 ≥ 20, which is not true.

So, the half plane is away from the origin. Also, x,y ≥ 0, so the region lies in the I quadrant.
On solving Eqs. (ii), (iii) and (iv), we get A(20,80), B(40,160) and C (20,180).

∴ Feasible region is ABC A

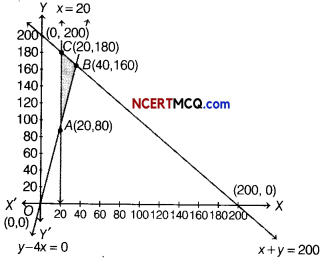
The comer points of the feasible region are A(20,80), B(40,160) and C(20,180).

The value of Z at the comer points are given below:

Corner points	Value of Z = 1000x + 600y
A(20, 80)	Z = 1000 x 20 + 600 x 80 = 68000
B(40,160)	Z = 1000 x 40 + 600×160 = 136000(Maximum)
C(20,180)	Z = 1000 x 20 + 600×180 = 128000

Thus, the maximum value of Z is 136000 at B(40,160).
Thus, 40 tickets of executive class and 160 tickets of economy class should be sold to maximise the profit and the maximum profit is ₹ 136000.

Case Based/Data Based

Question 14.
The order of a differential equation is the order of the highest order derivative appearing in the equation and the power of the highest order derivative is a degree.
On the basis of above information, answer the following questions.
(i) Find the order of the differential equation
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{3}\) + 5\(\left(\frac{d^{2} y}{d x^{2}}\right)^{5}\) – 5y = 0
Answer:
Given, differential equation is
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{3}\) + 5\(\left(\frac{d^{2} y}{d x^{2}}\right)^{5}\) – 5y = 0
Clearly, the highest order derivative present in the given differential equation is 3.

(ii) Find the sum of the order and degree of the differential equation
\(\sqrt[4]{\frac{d^{2} y}{d x^{2}}}=\sqrt{3 \frac{d y}{d x}}\)
Answer:
Given, a differential equation is

Here, the highest order derivative present in the given differential equation is 2, whose degree is 1.
∴ Required sum of order and degree = 2 + 1 = 3