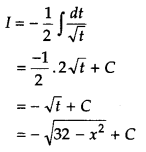CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 4 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
The population of a town grows at the rate of 10% per year. Using differential equation, find how long it will take for the population to grows 3 times.
Or
The marginal cost of producing x pairs of tennis shoes is given by MC = 60 + \(\frac{400}{x+1}\).
If the fixed cost is ₹ 3000, find the total cost function.
Answer:
Let P₀ be the population initially and P be the population after t yr,

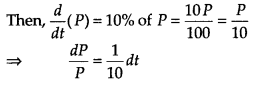
On integration both sides, we get
log P = \(\frac{1}{10}\) t + C
When t = 0, then P = P₀
∴ log P₀ = C
From Eq. (i), log P = \(\frac{t}{10}\) + log P₀
⇒ \(\log \left(\frac{P}{P_{0}}\right)=\frac{t}{10}\)
When the population grows 3 times i.e. P = 3 P₀, then log\(\left(\frac{3 P_{0}}{P_{0}}\right)\) = \(\frac{t}{10}\) ⇒ t = 10 log 3
Thus, it takes 10 log 3 years for the population to grow 3 times.

Or

C = 60x + 400 log |(x + 1)| + K ………. (i)
If x = 0, C = ₹ 3000
∴ 3000 = 0 + 400 log(1) + K
⇒ K = 3000
∴ C = 60x + 400 log |(x + 1)| + 3000 [from Eq. (i)]

Question 2.
A random sample of 36 workers is drawn from a factory to test, if their average monthly wages is ₹ 1500 or not. The population wages distribution is assumed to be normal with standard deviation of ₹ 300. The average monthly wages based on the 36 observations comes out to be ₹ 1800. Perform a test at 5% level of significance. Calculate test statistics.
Answer:
Consider, H₀ : µ = 1500
H₁ : µ ≠ 1500
x̄ = 1800, µ₀ = 1500,
σ = 300 and n = 36
∴ Test statistics,

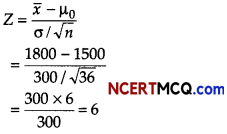
Question 3.
Find the present value of perpetuity of ₹ 900 at end of each quarter, if money is worth 6% compounded quarterly.
Or
To what sum will ₹ 16000 accumulate in 8 yr, if invested at an effective rate of 10%. [given (1.08)⁸ = 1.85]
Answer:
Given, R = ₹ 900
i = \(\frac{0.06}{4}\) = 0.015
Present value of perpetuity,
P = \(\frac{R}{i}=\frac{900}{0.015}\) = ₹ 60000
Or
We have, P = ₹ 16000,
i = \(\frac{8}{100}\) = 0.08
∴ S = P(1 + i)ⁿ
S = 16000(1 + 0.08)⁸
= 16000(1.08)⁸
= 16000(1.85) = 29600
Hence, the required sum is ₹ 29600

Question 4.
At what rate of interest will be present value of a perpetuity of ₹ 500 payable at the end of every 6 months be ₹ 10000?
Answer:
Let the rate of interest be r% per annum.
Then, i = \(\frac{r}{200}\)
Given, R = ₹ 500 and P = ₹ 10000
Using P = \(\frac{R}{i}\)
⇒ i = \(\frac{R}{P}\)
⇒ \(\frac{r}{200}=\frac{500}{10000}\) ⇒ r = 10
Hence, rate of interest is 10% per annum.

Question 5.
The corner points of the feasible region determined by the following systems of linear inequalities
2x + y ≤ 10, x + 3y ≤ 15, x ≥ 0 and y ≥ 0 are (0, 0), (5, 0), (3,4) and (0, 5).
Let Z = px + qy, when p, q ≥ 0, then find the relation between p and q so that the maximum of Z occurs at both points (3, 4) and (0, 5).
Answer:
The values of Z = px + qy at the points (3,4) and (0,5) are 3p + 4q and 5q, respectively.
As, Z has maximum value of both points (3, 4) and (0, 5), we get
3p + 4q = 5q ⇒ 3p = q ⇒ 3p – q = 0
which is the required relation between p and q.

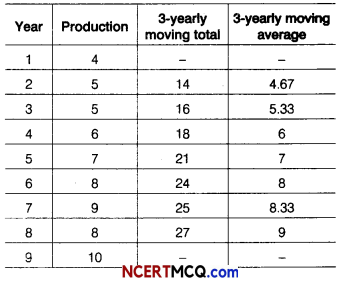
Question 6.
The production of a cement by a firm in 1 to 9 is given below.

Calculate the 3-yearly moving average.
Answer:
Calculation of 3-yearly moving average

Section – B [12 Marks]

Question 7.
Consider a hypothetical population comprising only four values 4, 6, 8 and 10. Find point estimation of population variance (σ²). Also, find standard error of sample variance (S²).
Answer:

Question 8.
Calculate the quarterly trend values by method of least square for quarterly data for last 5 yr given below.

Or
Apply the method of least squares to obtain the trend values from the following data.

Year	Sales (in lakh tonnes)
2006	100
2007	120
2008	110
2009	140

Also, predict the sales for the year 2013.
Answer:
Here, n = 5 (odd)
So, middle year i.e. 1966 is taken as origin, we will fit linear trend equation between average quarterly values (y) and time variable x (in year).

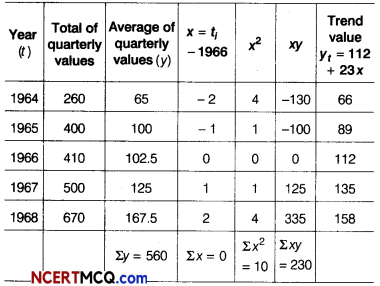
The normal equations for fitting linear trend equations.

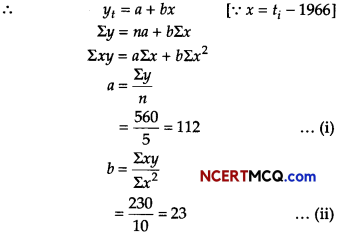
∴ Linear trend equation is y_t = 112 + 23 x
From Eqs. (i) and (ii), yearly increment in trend value = b = 23
Quarterly increment = \(\frac{23}{4}\) = 5.75
Here, n = 5 (odd)
So, middle year i.e. 2008 is taken as origin.

The equation of the straight line trend is
y_t = a + bx
Since, Σx = 0, a = \(\frac{\Sigma y}{n}\) = \(\frac{550}{5}\) = 110
and b = \(\frac{\Sigma x y}{\Sigma x^{2}}\) = \(\frac{-20}{10}\) = – 2
The required equation is,
y_t = 110 – 2x
For x = – 2,
y_t = 110 – 2(-2) = 114
Thus, for 2007 the trend value will be
114 – 2 = 112.

Question 9.
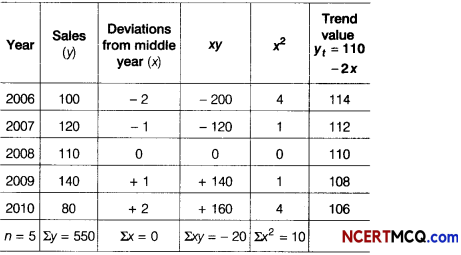
Surbhi borrowed a home loan amount of ₹ 150000 from a bank at an interest rate of 12% per annum for 3 yr. Find the monthly installment amount. She has to pay to the bank, [given, (1.01)^-36 = 0.698]
Answer:
If principle, P = ₹ 150000
i = \(\frac{12}{1200}\) = 0.01 and n = 12 × 3 =36
Let E be the monthly installment paid by Surbhi,

Question 10.
Supply function of a producer is given by 40 p = (x + 15)². Find the producer’s surplus, when the market price is ₹ 40.
Answer:
Given, the supply function is
40p = (x + 15)²
At p₀ = 40, we get
40 × 40 = (x₀ +15)²
⇒ x₀ + 15 = 40 ⇒ x₀ = 25
∴ Producer’s surplus,

Section-C [16 Marks]

Question 11.
Consider a bond with a coupon rate of 10% and annual coupons. The par value is ₹ 1000 and the bond has 5 yr to maturity. The yield to maturity is 11%. What is the value of the bond? [given, (1.11)^{– 5} = 0.593451]
Answer:
Given, face value of the bond (F) = ₹ 1000
Coupon rate (id) (annual) = 10% = 0.1
∴ R = F × id = 1000 × 0.1 = ₹ 100
Number of periods before redemption (n) = 5
and yield rate (i) = 11% =0.11.
We know that purchase value

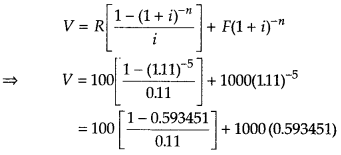
= 100(3.6959) + 593.451
= 369.59 + 593.40
= 962.99 ≅ 963
∴ The value of the bond is ₹ 963.

Question 12.
A propeller costs ₹ 180000 and its effective life is estimated to be 10 yr. A sinking fund is created for replacing the propeller by a new model at the end of its lifetime, when its scrap realises a sum of ₹ 34000 only. The price of the new model is estimated to be 30% more than the price of the present one. What amount should be put into the sinking fund at the end of each year, if it accumulates at 4% per annum compound interest? [given, (1.04)¹⁰ = 1.480]
Answer:
According to the question,
The present value of the machine is ₹ 180000.
Since, the price of new model is 30% more than the price of present machine.
∴ Price of new model 130
= \(\frac{130}{100}\) × 180000 = ₹ 234000
Scrap value of the present machine is ₹ 34000.
The net amount (A) to be paid after 10 yr for new model = 234000 – 34000 = ₹ 200000
Let the value of each sinking fund is a.
The rate of interest for 10 yr is
i = \(\frac{4}{100}\)
We know that
A = \(\frac{R}{i}\)[(1 + i)ⁿ – 1] …….. (i)
Now, we put the value of A, i and n in Eq. (i) to get the value of each instalment

Hence, the value of each sinking fund is ₹ 16666.67 to be paid at the end of each year.

Question 13.
There are two types of fertilisers F₁ and F₂, F₁ consists of 10% nitrogen and
6% phosphoric acid and F₂ consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds that she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F₁ costs ₹ 6 per kg and F₂ costs ₹ 5 per kg. Determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost? What is the minimum cost?
Or
Two godowns A and B have a grain storage capacity of 100 quintals and 50 quintals, respectively. They supply it to 3 ration shops D, E and F, whose requirements are 60, 50 and 40 quintals, respectively. The cost of transportation per quintal from godowns to the shops are given in the following table

How should the supplies be transported in order that the transportation cost is minimum?
Answer:
Suppose, the farmer uses x kg of F₁ and y kg of F₂. We have to construct the following table

Total cost of fertilisers,
Z = 6x + 5y
So, our problem is to minimise
Z = 6x + 5 y
Subject to constraints are,
\(\frac{x}{10}+\frac{y}{20}\) ≥ 14
⇒ 2x + y ≥ 280
\(\frac{6 x}{100}+\frac{10 y}{100}\) ≥ 14
⇒ 3x + 5y ≥ 700
and x, y ≥ 0
Table for line 2x + y = 280 is

X	0	140
y	280	0

So, line passes through the points (0, 280) and (140, 0)

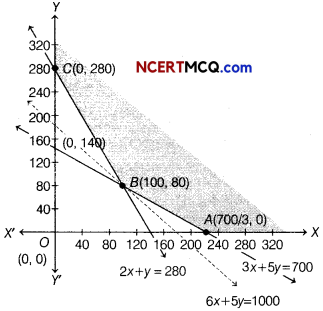
On putting (0, 0) in the inequality
2 x + y ≥ 280, we get
2 × 0 + 0 ≥ 280
⇒ 0 ≥ 280, which is not true.
So, the half plane is away from the origin.
Table for line 3x + 5y = 700 is

X	0	700/3
y	140	0

So, line passes through the points (0, 140) and \(\left(\frac{700}{3}, 0\right)\)
On putting (0, 0) in the inequality 3x + 5y ≥ 700,
we get 3 × 0 + 5 × 0 ≥ 700
⇒ 0 ≥ 700, which is not true.
So, the half plane is away from the origin.
Also, x, y ≥ 0, so the region lies in the 1 quadrant.
On solving the equations
2x + y = 280 and 3x + 5y = 700, we get B(100,80).
It can be seen that the feasible region is unbounded.
The corner points of the feasible region are
A\(\left(\frac{700}{3}, 0\right)\), B(100,80)and C(0,280).
The values of Z at the comer points are given below

Corner points	Value of Z = 6x + 5y
A\(\left(\frac{700}{3}, 0\right)\)	Z = 6 × \(\frac{700}{3}\) + 5 × 0 = 1400
B(100, 80)	Z = 6 × 100 + 5 × 80 =1000
C(0,280)	Z = 6 × 0 + 5 × 280 = 1400

As, the feasible region is unbounded, therefore 1000 may or may not be the minimum value of Z. For this, we draw a graph of the inequality 6x + 5y < 1000 and check whether the resulting half plane has points in common with the : feasible region or not.

It can be seen that the feasible region has no common point with 6x + 5y < 1000. Therefore, 100 kg of fertiliser F1 and 80 kg of fertiliser F₂ should be used to minimise the cost and the minimum cost is ₹ 1000.

Or

Let godown A supplies x and y quintals of grain to the shops D and E, respectively.
Then, (100 – x – y) will be supplied to shop F.
The requirement at shop D is 60 quintals, since x quintals are transported from godown A.
Therefore, the remaining (60 – x) quintals are transported from godown B. Similarly, (50 – y) quintals and 40 – (100 – x – y) = (x + y – 60) quintals will be transported from godown B to shops E and F, respectively. The given problem can be represented diagrammatically as follows

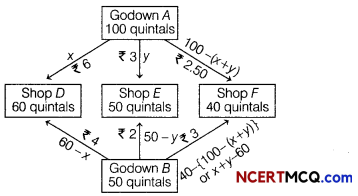
Let Z be the total cost of transportation, then
Z = 6x + 3y + 2.50 (100 – x – y) + 4 (60 – x) + 2 (50 – y) + 3 [(x + y) – 60]
= 6x + 3y + 250 – 2.50x – 2.50y + 240 – 4x + 100 – 2 y + 3x + 3 y – 180
= 2.50 x + 1.50y + 410 …(i)
Subject to constraints,
60 – x ≥ 0
or x ≤ 60 …(ii)
50 – y ≥ 0
or y ≤ 50 …(iii)
100 – (x + y) ≥ 0
or x + y ≤ 100 …(iv)
x + y – 6 ≥ 0
or x + y ≥ 60 …(v)
and x, y ≥ 0 …(Vi)
Table for line x + y = 100 is

x	100	0
y	0	100

So, line passes through the points (100, 0) and (0, 100).
On putting (0, 0) in the inequality x + y ≤ 100, we get
0 + 0 ≤ 100 ⇒ 0 ≤ 100, which is hue.
So, the half plane is towards the origin.
Table for line x + y = 60 is

X	0	60
y	60	0

So, line passes through the points (0, 60) and (60, 0).
On putting (0, 0) in the inequality x + y ≥ 60, we get
0 + 0 ≥ 60 ⇒ 0 ≥ 60, which is not hue.
So, the half plane is away from the origin.
Now, draw the graph of lines x = 60 and y = 50, which is perpendicular to X and Y-axes, respectively.
Clearly, the half planes x ≤ 60 and y ≤ 50 is towards Y and X-axes, respectively.
Also, x, y ≥ 0, so the region lies in the I quadrant.
The points of intersection of lines corresponding to Eqs. (ii), (iii), (iv) and (v) are
A(60, 0), B (60, 40), C (50, 50) and D (10, 50).
The graphical representation of these lines is given below

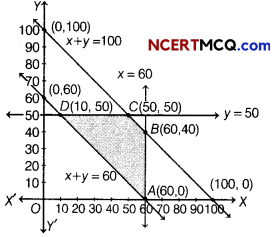
The shaded region in the graph represents the feasible region and its comer points are
A (60,0), B (60,40), C (50,50) and D (10,50).
The values of Z at the comer points are given below

Corner points	Value of Z =2.5x+1.5y + 410
A (60, 0)	Z =2.5(60)+ 1.5(0)+ 410 = 560
B (60, 40)	Z = 2.5(60) + 1.5 (40) + 410 = 620
C(50, 50)	Z = 2.5(50) + 15(50)+ 410 = 610
D (10, 50)	Z = 2.5(10)+ 1.5 (50)+ 410 = 510 (Minimum)

The minimum value of Z is 510 at D (10,50).
Thus, the amount of grain transported from A to D, E and F is 10 quintals, 50 quintals and 40 quintals, respectively and from B to D, E and F is 50 quintals, 0 quintal and 0 quintal, respectively.
The minimum cost is ₹ 510.

Case Based/Data Based

Question 14.
Following paragraph given to student by the teacher.
The given integral ∫ f(x)dx can be transformed into another form by changing the independent variable x to t by substituting x = g(t).
Consider, I = ∫ f(x) dx
On putting x = g(t), so that \(\frac{d x}{d t}\) = g'(t)
We write, dx = g'(t)dt
Thus, I = ∫ f(x)dx = ∫ f(g(t))g'(t)dt
This change of variable formula is one of the important tools available to us in the name of integration by substitution.
On the basis of above information, answer the following questions.
(i) Evaluate \(\int-\frac{d x}{x^{2}-16}\).
Answer:

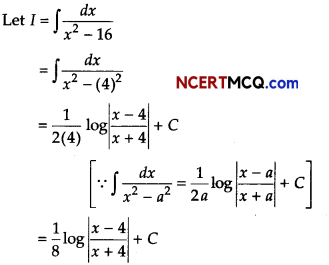
(ii) Evaluate \(\int \frac{x}{\sqrt{32-x^{2}}}\) dx.
Answer:
Let I = \(\int \frac{x}{\sqrt{32-x^{2}}}\) dx.
On putting
32 – x² = t
⇒ – 2xdx = dt
⇒ x dx = \(\frac{-1}{2}\) dt
Now,