CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 5 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 5 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 5 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
Evaluate

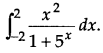
Or
The marginal cost function of producing x units of a product is given by
MC = \(\frac{x}{\sqrt{x^{2}+3600}}\). Find the total cost function and the average cost function, if the fixed cost is ₹ 1000.
Answer:

Question 2.
Calculate the 3-yearly moving average of the following data.

Answer:

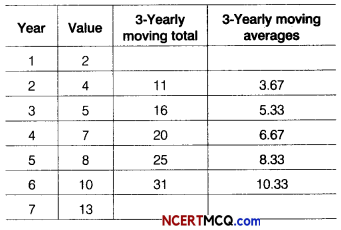
∴ 3-Yearly moving averages are 3.67,5.33,6.67, 8.33 and 10.33.

Question 3.
Find the effective rate of interest corresponding to 10% nominal rate compounded quarterly, [given (1.025) =1.1038]
Or
Find the present value of a sequence of payments of ₹ 4500 made at the end of every 6 months continuing, if money is worth 8% converted half-yearly.
Answer:
Given, nominal rate of interest,
r = 10% = 0.10
Since, interest is compounded quarterly.
∴ Number of conversion per year (m) = 4
We know that effective rate of interest
r_e = (1 + \(\frac{r}{m}\))^m – 1
= (1 + \(\frac{0.10}{4}\))⁴ – 1
= (1 + 0025)⁴ – 1
= (1025)⁴ – 1
= 1.1038 – 1
= 0.1038
= 10.38%

Or

Given, R = ₹ 4500
and rate of interest (r) = 8% = 0.08
Since, interest is compounded semi-annually.
∴ i = \(\frac{r}{2}=\frac{0.08}{2}\) = 0.04
Present value of an immediate perpetuity is
P = \(\frac{R}{i}\) ⇒ P = \(\frac{4500}{0.04}\)
= ₹ 112500

Question 4.
What sum of money invested now would establish a scholarship of ₹ 12000 to be awarded at the starting of each year to a deserving student, if money is worth 5% compounded annually?
Answer:
Given, R = ₹ 12000
i = \(\frac{5}{100}\) = 0.05

∴ Present value of a perpetuity due,
P = R(1 + i)
= 12000(1 + \(\frac{1}{0.05}\)
= 12000(1 + 20)= 12000 × 21= 252000
∴ Amount to be invested is ₹ 252000.

Question 5.
A random sample of size 25 has 60 as mean. The sum of squares of deviations from mean is 168, can this sample be regard as taken from the population having 64 as mean? Level of significance is 5%.
Answer:
Consider, H₀: µ = 64
H₁: µ > 64
n = 25, x̄ = 60, µ = M
and Σ(x_i – x̄)² = 168

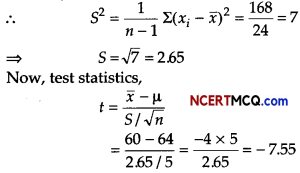
Degree of freedom =25- 1=24
∴ Tabulated value of t = 1.711
Since, calculated value |t| = 7.55 is greater than
the tabulated value, so H₀ is rejected.

Question 6.
Two tailors A and B earn ₹ 300 and ₹ 400 per day, respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day.
To find how many days should each of them work and if it is desired to produced at least 60 shirts and 32 pairs of trousers at a minimum labour cost. Formulate this problem as on LPP.
Answer:
Suppose, tailor A works for x days and tailor B works for y days.

The given data can be written in the tabulor form as follows

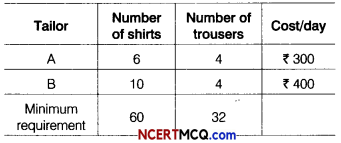
Required linear programming problem is Min Z = 300x + 400y
Subject to constraints are 6x + 10y ≥ 60,
4x + 4y ≥ 32 ⇒ x + y ≥ 8 and
x,y ≥ 0

Section – B [12 Marks]

Question 7.
Mr. Amit have set up a sinking fund in order to have ₹ 40000 in 12 yr for his son’s higher education. What amount he has to set aside at the end of every month into the fund paying 6% per annum compounded monthly? [given, (1.005)¹⁴⁴ = 205]
Answer:
Given, A = ₹ 40000
i = \(\frac{r}{12 \times 100}=\frac{6}{12 \times 100}\)
= 0.005
n = 12 × 12 = 144 months

∴ The monthly periodic payments,

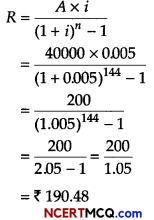
Question 8.
Find the f-test value for the following two samples from a population.
Set-I 6, 8, 5, 7
Set-II 4, 6, 5, 8
Answer:
x̄ = \(\frac{6+8+5+7}{4}=\frac{26}{4}\) = 6.5
and ȳ = \(\frac{4+6+5+8}{4}=\frac{23}{4}\) = 5.75

∴ S² = \(\frac{1}{n_{1}+n_{2}-2}\)[Σ(x – x̄)² + Σ(x – ȳ)²]
= \(\frac{1}{6}\)[5 + 8.9325]

Here, Σ(x – x̄)² = (-0.5)² + (1.5)²
+ (-1.5 )² + (0.5 )² = 0.25 + 2.25 + 2.25 + 0.25 = 5
and Σ(x – ȳ)² = (-1.75)² + (0.5)² + (- 0.75)² + (2.25 )²
= 306 + 0.25 + 0.5625 + 5.06 = 8.9325
⇒ S² = \(\frac{1}{6}\) (13.9325) = 2.3220 ⇒ S = 1.52

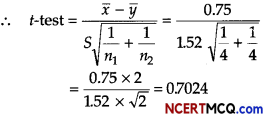
Question 9.
Consider the following data

Calculate 3-days moving average and display these and the original figures on the same graph.
Answer:
Given, table is shown below:

Dates in April	Number of unit sold
12	2
13	5
14	0
15	12
16	13
17	25
18	45
19	13
20	31
21	18
22	11
23	2
24	3
25	1

On the basis of above data, we can draw the following graph.

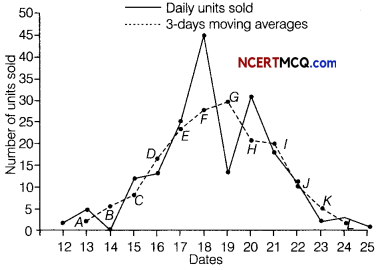
Question 10.
The demand function of a product is p = 10e^-x. Find the consumer’s surplus, when the market price at p₀ = 1. [given, log₁₀ e = 0.4343]
Or
The demand and supply functions for a commodity are p = x² – 6x +16 and p = \(\frac{x^{2}}{3}+\frac{4 x}{3}\) + 4, respectively. Find the equilibrium point assuming x ≤ 5.
Answer:
The demand function is p = 10e^-x
It is given that p₀ = 1
On putting the value of p₀ = 1 in p = 10e^-x, we get
I = 10e^-x ⇒ e^-x = 10
⇒ x = log_e10
∴ x₀ = log_e10

Then, consumer’s surplus is given by

Or
The demand and supply functions are p= D(x) and p = S(x),
where D(x) = x² – 6x +16 and S(x) = \(\frac{x^{2}}{3}+\frac{4 x}{3}\) + 4

The equilibrium point (x0, p0) is the point at which the demand supply curves intersect
∴D(x) = S(x)
x² – 6x +16 = \(\frac{x^{2}}{3}+\frac{4 x}{3}\) + 4
\(\frac{2}{3}\)x² – \(\frac{22}{3}\)x + 12 + 0
x² – 11x + 18 = 0
(x – 2)(x – 9) = 0 ⇒ x = 2 [∵ x ≤ 5]
On putting x = 2 in D(x), we get
P = (2 )² – 6(2) + 16
p = 4 – 12 + 16 = 8
Hence, (2, 8) is the equilibrium point.

Section – C [16 Marks]

Question 11.
If Mr. Nirav deposits ₹ 250 at the beginning of each month in an account that pays an interest of 6% per annum compounded monthly, how many months will be required for the deposit to amount to at least ₹ 6390?
Answer:
Given, Mr. Nirav deposit amount per month is a = ₹ 250
The total amount of annuity is (M) = ₹ 6390
Rate of interest, r = 6% = \(\frac{6}{100}\) per annum

Let the number of months be n.
We know that

⇒ 0.127164 + 1 = (1.005)ⁿ
⇒ 1.127164 = (1.005)ⁿ
Taking log on both sides of Eq. (i), we get
log 1.127164 = n log 1.005
⇒ n = \(\frac{\log (1.127164)}{\log (1.005)}\) = 24110075
∴Number of months required = 24 months

Question 12.
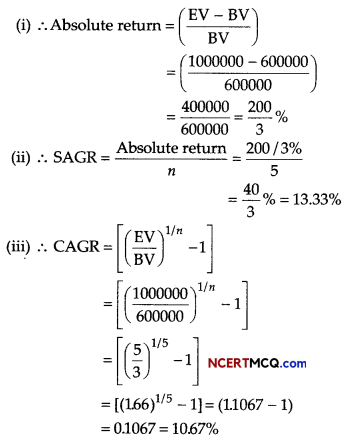
Mr. Ankit has invested ₹ 6 lakhs in a financial plan and after the completion of 5 yr. He received a sum of ₹ 10 lakhs. Find
(i) the absolute return.
(ii) the simple annual growth rate (SAGR).
(iii) the compound annual growth rate (CAGR). [given, (1.66)^1/5 =1.1067]
Answer:
Given, BV = ₹ 600000
EV = ₹ 1000000
n = 5 yr

Question 13.
In a bank principal increases at the rate of 5% per year. An amount of ₹ 1000 is deposited with this bank, how much will it be worth after 10 yr (given, e^0.5 = 1.648)?
Or
Suppose, it is given that the rate at which some bacteria multiply is proportional to the instantaneous number present. If the original number of bacteria triples in three hours. In how many hours will it be four times.
Answer:
Let P and t be the principal and time, respectively.
It is given that the principal increases continuously at the rate of 5% per year.
So, \(\frac{d P}{d t}\) = 5%of P ⇒ \(\frac{d P}{d t}=\frac{5}{100}\)P
On separating the variable, we get \(\frac{d P}{P}=\frac{1}{20}\) dt

On integrating both sides, we get
∫ \(\frac{d P}{P}\) = ∫ \(\frac{1}{20}\) dt ⇒ log |P| = \(\frac{1}{20}\)t + C …(i)
When t = 0, P = ₹ 1000 (initialy) this
log 1000 = C …(ii)
On putting the value of C in Eq. (i), we get

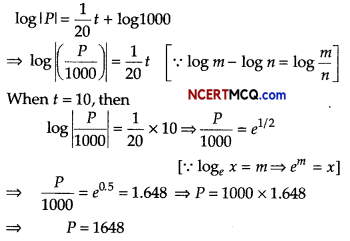
Hence, after 10 yr, the amount will worth ₹ 1648

Or

Let the original count of bacteria be N₀ and at any time the count of bacteria be N.
Then, \(\frac{d N}{d t}\) ∝ N ⇒ \(\frac{d N}{d t}\) = kN ⇒ \(\frac{d N}{N}\) = kdt

On integrating both sides, we get
∫\(\frac{d N}{N}\) = ∫kdt
⇒ logN = kt + C
⇒ N = e^kt+C
⇒ N = e^Ce^kt
⇒ N = Aêt
When t = O, then N = N₀, we get A = N₀
∴ N = N₀e^kt
When t = 3, N = 3N₀
∴ 3N₀ = N₀e^3k ⇒ e^3k = 3
= e^k = (3)e^1/3
When N = 4N₀
∴ 4N₀ = N₀e^kt
⇒ e^kt = 4
⇒ (3^1/3)^t = 4
⇒ t = \(\frac{3 \log 4}{\log 3}\)h

Case Based/Data Based

Question 14.
A company manufactures three kinds of calculators A, B and C in its two factories I and II. The company has got an order for manufacturing atleast 6400 calculators of kind A, 4000 of kind B and 4800 of kind C. The daily output of factory I is of 50 calculators of kind A, 50 calculators of kind B and 30 calculators of kind C.
The daily output of factory II is 40 calculators of kind A, 20 of kind B and 40 of kind C. The cost per day to run factory I is ₹ 12000 and of factory II is f 15000. Let factory71 run x days and factory II run y days.
On the basis of above information, answer the following question.
(i) Formulate this problem as an LPP.
Answer:
Total cost (in ₹) = 12000x + 15000y
Then, minimise Z = 12000x + 15000y

Subject to constraints are,
50x + 40y ≥ 6400 or 5x + 4y ≥ 640 …(i)
50x +20y ≥ 4000 or 5x +2y ≥ 400 …(ii)
30x + 40y ≥ 4800 or 3x + 4y ≥ 480 …(iii)
and x ≥ 0, y ≥ 0 …………(iv)

(ii) How many days do the factory I has to be in operation to produce the order with the minimum cost?
Answer:
The above Eqs. (i), (ii), (iii) and (iv) can be represented graphically as

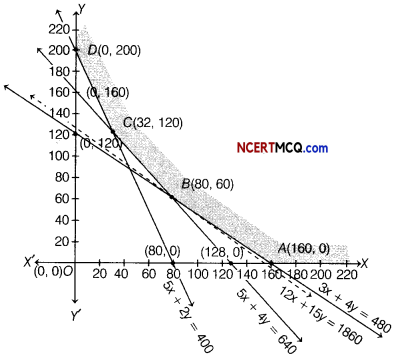
Clearly, the feasible region ABCD (shaded region), where comer points are A (160,0), B(80,60), C(32,120)and D(0,200)is unbounded.

The values of Z at comer points are given below:

Corner points	Value of Z = 12000X + 15000y
A(160, 0)	Z = 12000 × 160 + 15000 × 0 = 1920000
B(80, 60)	Z = 12000 × 80 + 15000 × 60 = 1860000 (Minimum)
C(32,120)	Z = 12000 × 32 + 15000 × 120 = 2184000
D(0, 200)	Z = 12000 × 0 + 15000 × 200 = 3000000

In the above table, we find that minimum value of Z is 1860000 occur at the point B (80,60).
But we cannot say that it is a minimum value of Z as region is unbounded.

Therefore, we have to draw the graph of the inequality
12000x + 15000y < 1860000
or
12x + 15y < 1860
or
\(\frac{x}{155}+\frac{y}{124}\) < 1

Now, check whether the resulting open half plane has any point common with feasible region. From figure, we see that it has no point in common.

Thus, the minimum value of Z is ₹ 1860000 attained at the point B(80,60).
Hence, factory I should run for 80 days.