CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 7 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 7 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 7 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
A population grows at the rate of 5% per year. How long does it take for the population to double?
Answer:
Let P₀ be the initial population and the population after t yr be P.
According to given problem, we get
\(\frac{d P}{d t}=\left(\frac{5}{100}\right)\) × P = \(\frac{d P}{d t}=\frac{P}{20}\)
Now, separating the variables, we get
\(\frac{d P}{P}=\frac{d t}{20}\)
On integrating both sides, we get
l0gP = \(\frac{t}{20}\) + C₁
⇒ P = ^{et/20 + C₁} = e^t/20 – e^C₁ = Ce^t/20, where e^C₁ = C
∵ At t = 0, P = P₀, therefore we have P₀ = C.e⁰

Question 2.
The mean and variance of a random sample of 81 observations were computed as 200 and 144, respectively. Compute the 95% confidence limits for population mean.
Or
The mean weekly sales of mango candy in candy stores was 225.4 mango candy per store. After an advertising campaign the mean weekly sales in 25 stores for a typical week increased to 237.6 and showed a standard deviation of 21.3 was the advertising campaign successful? Level of confidence 5%. [given, t₂₄ (0.05) = 1.711]
Answer:
Given, n = 81, x̄ = 200 and σ² = 144 ⇒ σ = 12
∴ Confidence limits (95%) are
⇒ x̄ ± 1.96\(\left(\frac{\sigma}{\sqrt{n}}\right)\) = x̄ ± 1.96\(\left(\frac{12}{\sqrt{81}}\right)\)
= [200 – 1.96 \(\left(\frac{12}{9}\right)\),200 + 1.96 \(\left(\frac{12}{9}\right)\)]
= [200 – 2.61,200 + 2.61]
= [197.39,202.61]

Or

Given, n = 25, x̄ = 237.6, μ = 225.4 and S = 21.3
Consider, H₀ : μ = 225.4 and H₁ : μ > 225.4

Now, test statistics,
t = \(\frac{\bar{x}-\mu}{S / \sqrt{n}}\)
= \(\frac{237.6-225.4}{21.3 / \sqrt{25}}=\frac{12.2 \times 5}{21.3}\) = 2.86

Since, calculated value of t > tabulated value of t. Hence, H₀ can rejected
⇒ Advertising campaign was successful.

Question 3.
Anand Prasad borrows a sum of ₹ 225000 at an interest rate of 10% (flat) for a tenure of 5 yr. Calculate his EMI.
Or
A sum of ₹ 75000 invested at r% compounded quarterly will provide payments of ₹ 800 each at the end of 3 months. Find the value of r.
Answer:
Given, principal (P) = ₹ 225000
Interest (yearly) = 10% of 225000 = ₹ 22500
Interest for 5 yr = 5 × 22500 =112500
⇒ EMI = \(\frac{225000+112500}{5 \times 12}=\frac{337500}{60}\)
[∵ EMI = \(\frac{\text { Principal + Interest }}{n}\)]
= 5625
∴ Hence, EMI is 15625.

Or

Given, present value (P) = ₹ 75000
Let the rate of interest be r.
Since, interest compounded quarterly
∴ i = \(\frac{r}{4}\)
Periodic payment (R) = ? 800

We know that
P = \(\frac{R}{i}\)
⇒ 75000 = \(\frac{800}{i}\)
⇒ i = \(\frac{800}{75000}\)
⇒ i = 0.010
⇒ \(\frac{r}{4}\) = 0.010 4
⇒ r = 0.040
= 4% (approx.)

Question 4.
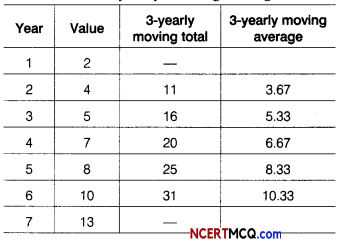
Calculate the 3-yearly moving averages of the following data.

Answer:
Calculation of 3-yearly moving averages.

Question 5.
What amount is recieved at the end of every 6 months forever, if ₹ 72000 kept in a bank earns 8% per annum compounded half-yearly.
Answer:
It is given that the present value of perpetuity of ₹ R payable at the end of each 6 months is ₹ 72000. If money is worth 8% compounded semi-annually. Thus,
We have, P = ₹ 72000
and i = \(\frac{8}{200}\) = 0.04
∵ P = \(\frac{R}{i}\)
⇒ R = Pi
⇒ R = 72000 × 0.04 = 2880
Hence, R is ₹ 2880

Question 6.
Find the maximum value of Z for the problem maximise Z = 2x + y subject to constraints are x + y ≤ 2, x ≥ 0, y ≥ 0 is
Answer:
We have, maximize Z = 2 x + y

Subject to constraints are
x + y ≤ 2, x ≥ 0, y ≥ 0

The shaded region shown in fig OAB is bounded and the coordinates of comer points O, A and B are (0, 0), (2,0) and (0, 2), respectively.

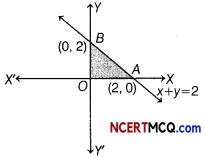
Comer points	Value of Z =2x+y
(0,0)	0
(2,0)	4 (Maximum)
(0, 2)	2

Section – B [12 Marks]

Question 7.
A product can be manufactured at a total cost C(x) = \(\frac{x^{2}}{100}\) + 100x + 40, where x is the number of units produced. The price at which each unit can be sold is given by p = (200 – \(\frac{x}{100}\)). Determine the production level x at which the profit is maximum. What is the price per unit and total profit at the level of production?
Answer:
Given, total cost C(x) = \(\frac{x^{2}}{100}\) + 100x + 40
Price of each unit can be sold
p = 200 – \(\frac{x}{100}\)

Price of x unit sold
R(x) = px = 200x – \(\frac{x^{2}}{400}\)

∴ Profit P(x) = R(x) – C(x)
= 200x – \(\frac{x^{2}}{400}-\frac{x^{2}}{100}\) – 100x – 40
⇒ P(x) = \(\frac{x^{2}}{80}\) + 100x – 40 ……..(i)

On differentiating both sides w.r.t. x, we get
P'(x) = \(\frac{2x}{80}\) + 100
= – \(\frac{x}{40}\) + 100

For maxima or minima, put P'(x) = 0
⇒ – \(\frac{x}{40}\) + 100 = 0
x = 4000
Now, P”(x) = – \(\frac{1}{40}\) < 0

Hence, P(x) is maximum when x = 4000.
Total profit at x = 4000, then
P(4000) = \(\frac{-(4000)^{2}}{80}\) + 100(4000) – 40 [from Eq. (i)]
= -200000 + 400000 – 40
= 199960
Hence, the total profit is ₹ 199960.

Question 8.
Ten oil tins are taken at random from an automatic filling machine. The mean weight of the tins is 17.2 kg and standard deviation is 0.62 kg. Does the sample mean differ significantly from the intended weight of 18 kg? [given, t₉(0.05) = 2.26]
Answer:
Given, n = 10, x̄ = 17.2, μ = 18 and S = 0.62
Consider, H₀: μ = 18
H₁: μ ≠ 18
t = \(\frac{\bar{x}-\mu}{S / \sqrt{n}}\)
= \(\frac{17.2-18}{0.62 / \sqrt{10}}\)
= –\(\frac{0.8 \times \sqrt{10}}{0.62}\) = -4.08

Since, calculated value of If |t| is greater than the tabulated value of t. So, H₀ is not accepted. Thus, the difference between sample mean weight and the intended weight is not insignificant.

Question 9.
Below are given the figures of production (in thousand tonnes) of a sugar factory.

Fit a straight line trend by the method of least squares and find trend value for year 2005.
Or
Consider the following data

Calculate 3-days moving average and display these and the original figures on the same graph.
Answer:
Here, n =7 (odd)
So, we shift the origin to the middle of the time period of the 2008.

Let the straight line trend of y on x be
y_t = a + bx …(i)

Now, construct the table as under.

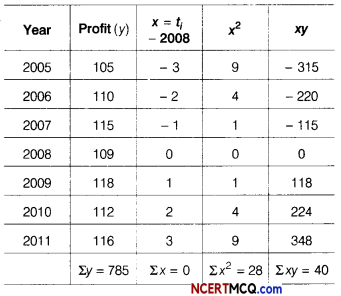
Now, a = \(\frac{\Sigma y}{n}=\frac{785}{7}\) = 112.14
and b = \(\frac{\Sigma x y}{\Sigma x^{2}}=\frac{40}{28}\) = 1.43

So, the required equation of the straight line trend is
y_t = 112.14 + 1.43x

:. Trend value for year 2005,
y_t = 112.14 + 1.43(- 3)
= 112.14 – 4.29
= 107.85

Or

According to the question,
Let the 3-days moving average is m.


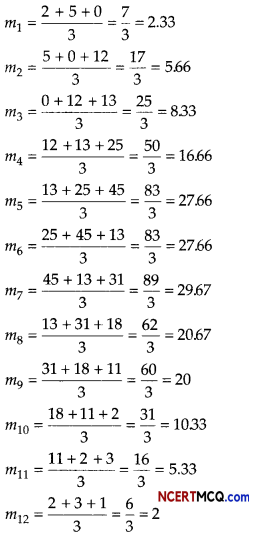
On the basis of above data we can draw the following graph:

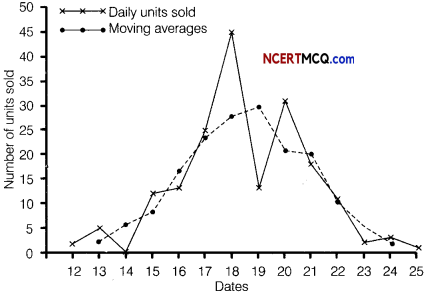
Question 10.
Mr. Narayan Sankar has invested ₹ 150000 in a financial plan whose compound annual growth rate (CAGR) is 8.5% and he received a final value of ₹ 300000.
Find the period (completed) for which he has invested the amount. [given, log 2 = 0.3010 and log(1.09) = 0.0374]
Answer:
10. Given, EV = ₹ 300000
BV = ₹ 150000 and CAGR = 8.5%

We know that
CAGR = [\(\left(\frac{\mathrm{EV}}{\mathrm{BV}}\right)^{1 / n}\) – 1] × 100
⇒ 8.5 = [\(\left(\frac{300000}{150000}\right)^{1 / n}\) – 1] × 100
⇒ 8.5 = [(2)^1/n – 1] × 100
⇒ 8.5 = (2)^1/n × 100 – 100
⇒ 8.5 + 100 = (2)^1/n × 100
⇒ 108.5 = (2)^1/n × 100
⇒ (2)^1/n = \(\frac{108.5}{100}\) = 1.085
⇒ \(\frac{1}{n}\) log2 = log(1.09)
⇒ n = \(\frac{\log 2}{\log (1.09)}\)
⇒ n = \(\frac{0.3010}{0.0374}\)
⇒ n = 8.0481
⇒ n = 8
∴ The period for which he has invested the amount is 8 yr.

Section – C [16 Marks]

Question 11.
A machine is bought for ₹ 320000. Its effective life is 8 yr, after which its salvage value would be ₹ 25000. It is decided to create a sinking fund to replace this machine at the end of its effective life by making half yearly payments that will earn an interest of 8% per annum compounded half yearly. If it is known that the cost of machine increases by 5% per annum. Calculate the amount of each payment to the sinking fund. [given (1.04)¹⁶ =1.8730 and (1.05)⁸ =1.4774]
Or
A bond has face value of ₹ 10000 and maturity period of 10 yr. The nominal interest rate is 6% per annum. What should be the price of the bond to yield an effective interest of 8%? [given (1.08)^-0 = 0.4631]
Answer:
Let each semi-annually deposit in the sinking fund of ₹ R. Since, the cost of new machine is increases by 5% per annum the cost of present.
Cost of machine at present = ₹ 320000
Cost of machine after increasing 5% per annum after 8 yr
= 32000o\(\left(1+\frac{5}{100}\right)^{8}\)
= 32000 (1.05)⁸
= 320000 × 1.4774
= ₹ 472768
Salvage value of present machine = ₹ 25000
So, net amount required at the end of 8 yr to purchase the new model is ₹ (472768 – 25000) = ₹ 447768

We know that R = \(\frac{i \times S}{(1+i)^{n}-1}\)
Here, S = ₹ 447768, n = 8 × 2 = 16 yr
i = \(\frac{8}{200}\) = 0.04
∴ R = \(\frac{(0.04) \times(447768)}{(1+0.04)^{16}-1}\)
= \(\frac{17910.72}{(1.04)^{16}-1}\)
= \(\frac{17910.72}{18730-1}\)
= \(\frac{17910.72}{0.8730}\) = 20516.28
Thus, ₹ 20516.28 deposited half yearly out of the profit to purchase the new model of the machine.

Or

We have, F = Face value of bond = ₹ 10000
N = Number of period = 10
C = Coupon payment = Annual dividend × 10000
= \(\frac{6}{100}\) × 10000 = 1600
F = Maturity value = Face value = ₹ 10000

Let PV be the price of the bond.

Hence, the price of bond is ₹ 8657.75.

Question 12.
The supply function of a producer is given by p = \(\frac{2}{5}\) e^2x, where x denotes thousand units. Find producer’s surplus when sales are 2000 units.
Answer:
The supply functions is p = \(\frac{2}{5}\) e^2x
When sales are 2000 units i.e., x₀ =2, we get

Question 13.
Anil wants to invest atmost ₹ 12000 in bonds A and B. According to the rules, he has to invest atleast ₹ 2000 in bond A and atleast ₹ 4000 in bond B. If the rate of interest in bond A is 8% per annum and on bond B is 10% per annum, then to maximise the interest, then find the investment in bond A and B.
Answer:
Let the investment in bond A and B are x and y respectively.
Then, our problem is to Maximise Z = 0.08x + 0.10y
Subject to constraints are
x + y ≤ 12000, x ≥ 2000
y ≥ 4000 and x, y ≥ 0

The graph of the above inequality is given by

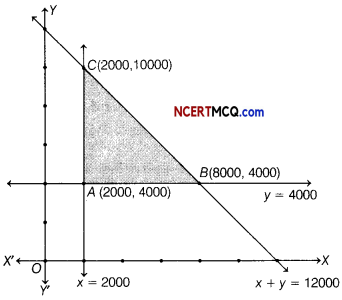
In the above graph shaded region is the feasible bounded region ABC.
Now, the values of Z at the comer points are given by

Corner point	Value of Z = 0.08x + 0.10 y
(2000, 4000)	560
(8000, 4000)	1040
(2000, 10000)	1160 (Maximum)

From the above table, we see that the maximum value of Z is 1160 which occurs at the point (2000,10000).
Hence, to maximise the interest ₹ 2000 and ₹ 10000 must be invested in bond A and B, respectively.

Case Based/Data Based

Question 14.
EMI is a part of equally divided monthly outgoes to clear off an outstanding loan within a stipulated time frame. For a fixed interest rate loan, the EMI remain fixed for the entire tenure of the loan, provided there is no default or part payment in between. The EMI is used off both the principal and interest components of an outstanding loan, The first EMI has the highest interest component and the lowest principal component.

Rajesh purchased a house from a company for ₹ 2500000 and made a down payment of ₹ 500000. He repays the balance in 25 yr by monthly installments at the rate of 9% per annum compounded monthly, (given (1.0075)_300 = 0.1062)
(i) What are the monthly payment?
(ii) What is the total interest payment?
Answer:
Cost of house = ₹ 2500000
Down payment = ₹ 500000
Principal amount = ₹ (2500000 – 500000)
= ₹ 2000000,
n = 25 × 12 = 300
and i = \(\frac{9}{1200}\) = 0.0075

(i) We know that

Hence, monthly payment is ₹ 16782.27

(ii) We have, EMI = ₹ 16782.27
n = 300 and P = ₹ 2000000
Total interest = n × EMI – P
= 300 × 16782.27 – 2000000
= 5034681 – 2000000
= 3034681
Hence, total interest is ₹ 3034681.