CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 8 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 8 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 8 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
The feasible region (shaded) for a LPP is shown in the following figure

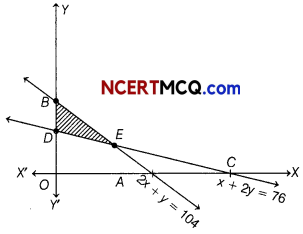
Find the maximum value of Z = 3x + 4y.
Answer:
As clear from the graph comer points are O, A, E, D with coordinates (0, 0), (52, 0), (44, 16) and (0, 38).

Corner points	Z = 3x + 4y
0(0,0)	0
4(52, 0)	156
£(44,16)	196 (Maximum)
D(0, 38)	152

Hence, the maximum value of Z is 196 at E(44, 16)

Question 2.
Find the force of interest corresponding to the effective rate 11%.
[given, log(1.11) = 0.0453 and log e = 0.4342]
Answer:
Given, r_e = 11% = 0.11
We know that, r_e = e^r – 1
∴ 0.11 = e^r – 1
⇒ e^r = 1.11
Taking log on both sides,
r log e = log(1.11)
⇒ r(0.4342) = 0.0453
⇒ r = \(\frac{0.0453}{0.4342}\)
= 0.1043 = 10.43%
∴ The force of interest is 10.43%.

Question 3.
An asset costing ₹ 95000 is expected to have a useful life of 8 yr, has final annual depreciation of ₹ 8000. Find the final scrap value of asset.
Answer:
Given, D = ₹ 8000, C = ₹ 95000 and n = 8 yr
We know that, D = \(\frac{C-S}{n}\)
∴ 8000 = \(\frac{95000-S}{8}\)
⇒ 95000 – S = 8000 × 8
⇒ 95000 – S = 64000
⇒ S = 95000 – 64000
⇒ S = ₹ 31000
∴ Final scrap value of the asset is ₹ 31000.

Question 4.
A manufacturer’s marginal cost is \(\frac{600}{\sqrt{5 x+36}}\). Find the cost involved to increase production from 150 units to 450 units.
Or
The marginal revenue function of a commodity is given MR = 12 – 3x² + 4x.
Find the total revenue from the sale of 4 units.
Answer:
Given, marginal cost (MC) = \(\frac{600}{\sqrt{5 x+36}}\)
⇒ \(\frac{d C}{d x}=\frac{600}{\sqrt{5 x+36}}\)
⇒ \(\frac{600}{\sqrt{5 x+36}}\)
Cost involved to increases production from 150 units to 450 units is,

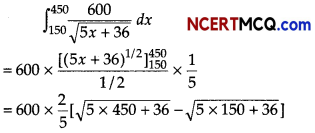
= 240 [√2286 – √786]
= 240 (47.81 – 28D3)
= 240 × 1978
= ₹ 4747.2
Or
We have, MR = 12 – 3x² + 4x
∵ ∫dr = ∫MR dx [∵ MR = \(\frac{d R}{d x}\)
We know that when x = 0, then R = 0
∵ K = 0
R = 12x – x³ + 2x² [from Eq. (i)]
Now, the total revenue from the sale of 4 units is given by put x = 4
R = 48 – 64 + 32 = 16

Question 5.
Consider the following hypothesis
H_o: μ = 315 and H_a: μ ≠ 315
A sample of 60 provided a sample mean of 324.6. The population standard is 14 and level of significance α = 0.05. Check the hypothesis test given above, using interval estimation.
Answer:
Given, μ_o = 315, n = 60, x̄ = 324b
σ = 14 and α = 0.05
∴ Confidence interval = x̄ ± Z_α/2\(\frac{\sigma}{\sqrt{n}}\)
= 324.6 ± 1.96 × \(\frac{14}{\sqrt{60}}\) [∵ Z_α/2 = Z_0.025 = 1.96]
∴ Confidence interval
= 324.6 ± 1.96 × 131
= 324.6 ± 3.54
= (324.6 – 3.54,324b + 3.54)
= (32136, 328.14)
Since, the hypothesis value of population mean p0 = 315 does not lies in confidence interval, so H₀ rejected.

Question 6.
For the following series of observations

Calculate 5- yearly moving averages.
Or
The data below shows the figures of income of a municipal corporation over the years.

Calculate 4-yearly centred moving averages.
Answer:

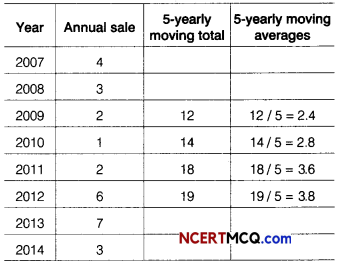
∴ 5-yearly moving averages are 2.4, 2.8, 3.6 and 3.8
OR

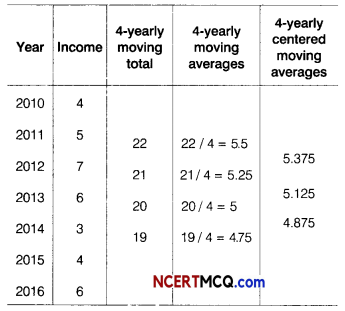
∴ 4-yearly centred moving averages are 5.375, 5.125 and 4.875.

Section – B [12 Marks]

Question 7.
The average nicotine content of a particular brand of cigarette is supposed to be 2.2 mg per cigarette. A smoker of this brand wants to see, if it is really 2.2 mg or more. With this purpose the nicotine contents of 50 cigarettes are measured. The sample mean based on 50 cigarettes is 2.95 mg per cigarette. The population standard deviation is 0.8 mg. Do the data provide enough evidence that the average nicotine content exceeds 2.2 mg? Test at 5% level using p-value approach and critical value approach, [given, Z_0.05 = 1.645]
Answer:
Consider H₀ : μ = 2.2
H_a :μ > 2.2
x̄ = 2.95, μ₀ = 2.2,
n = 50 and σ = 0.8
∴ Test statistics,

Since, |t| > Z_0.05
So, reject H₀ at 5% level.
Means provide sufficient evidence to conclude that average nicotine content exceeds 1.5 mg per cigarette.

Question 8.
Fit a straight line trend for the following data and find the trend values. Estimate the sales for 2018.

Answer:
Table for fitting straight line trend

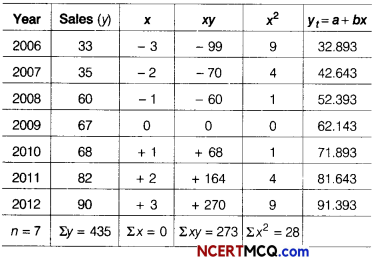
The equation of the straight line trend is
y_t = a + bx
∴ a = \(\frac{\Sigma y}{n}=\frac{435}{7}\) = 62.143
∴ b = \(\frac{\Sigma x y}{x^{2}}=\frac{273}{28}\) = 9.75
y = 62.143 + 9.75x
Hence, y₂₀₀₆ = 62.143 + 9.75(-3)
= 62.143 – 29.25 = 32893
y₂₀₀₇ = 62.143 + 9.75 (- 2)
= 62.143 – 19.5 = 42.643, etc.
For 2018, x shall be + 9,
y₂₀₁₈ = 62.143 + 9.75(9)
= 62.143 + 87.75 = 149.893
The estimated sales for the year 2018 is ₹ 149.893 lakh.

Question 9.
Rohit has taken a loan of ₹ 600000 with interest rate 10% for the period of 12 yr. Find (reducing) EMI for the above data. [given (1.0083)¹² = 1.1043]
Or
What nominal rate compounded quarterly will be equivalent to 12% compounded continuously? [given e^0.12 = 1.1274]
Answer:
Given, P = ₹ 600000, n = 12 yr
Interest rate = 10% (per annum)
Monthly interest rate (r) = \(\)
= \(\frac{0.10}{12}\) = 0.0083

OR

⇒ \(\left(1+\frac{r}{4}\right)\) = antilog (0.0134)
= 1.031
⇒ \(\frac{r}{4}\) = 0.031
⇒ r = 0.124
⇒ r = 12.4%

Question 10.
A manufacturer’s marginal revenue function is given by MR = 275 – x – 0.3x². Find the increase in the manufacturer’s total increase in revenue, if the production is increased from 10 to 20 units.
Answer:
We have
⇒ MR = 275 – x – 0.3x²
⇒ \(\frac{d R}{d x}\) = MR
⇒ \(\frac{d R}{d x}\) = 275 – x – 0.3x²
We have to find the total increase in revenue, if the production is increased from 10 to 20 units i.e. we have to
R(20) – R(10)

Hence, increase in revenue is ₹ 1900

Section – C [16 Marks]

Question 11.
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 h and that of second machine is 9 h per day.
Each unit of product A requires 3 h on both machines and each unit of product B requires 2 h on first machine and 1 h on second machine. Each unit of product A is sold at a profit of ₹ 7 and B at a profit of ₹ 4. Find the production level per day for maximum profit graphically.
Answer:
Let the manufacturer produces the products A and B be x and y units, respectively.
We construct the following table

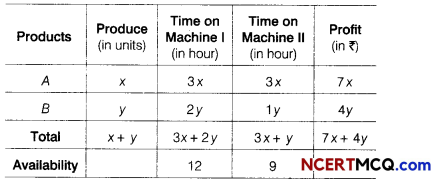
Here, total profit Z = 7x + 4y
i.e. maximise Z = 7x + 4y …(i)
Subject to the constraints are
3x + 2y ≤ 12
3x + y ≤ 9 and x ≥ 0, y ≥ 0
Now, consider the given inequations as equations
3x + 2y = 12 …(ii)
3x + y = 9 …….. (iii)
Table for line 3x + 2y = 12 or y = \(\frac{12-3 x}{2}\) is

X	0	4
y	6	0

It passes through the points (0, 6) and (4, 0).
On putting (0, 0) in the inequality 3x + 2 y ≤ 12,
we get
0 + 0 ≤ 12 ⇒ 0 < 12 [true]
So, the half plane is towards the origin.
Table for line 3x + y = 9 or y = 9 – 3x is

X	0	3
y	9	0

It passes through the points (0, 9) and (3, 0).
On putting (0, 0) in the inequality 3x + y ≤ 9, we get
0 + 0 ≤ 9 ⇒ 0 ≤ 9 [true]
So, the half plane is towards the origin.
Also, x ≥ 0 and y ≥ 0, so the region lies in 1st quadrant.
Now, the intersection point of lines (i) and (ii) is
(3x + 2y) – (3x + y) = 12 – 9
⇒ y = 3
and 3x = 12 – 2 × 3
⇒ 3x = 12 – 6
⇒ x = 2
Thus, the point of intersection is B (2, 3).
The graph of inequations is shown below

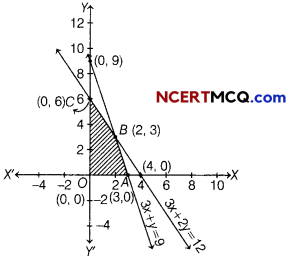
Here, we see that OABC is a required feasible region, whose comer points are O(0,0), A(3, 0), B(2, 3) and C(0, 6).
The values of Z at these comer points are as follows

Corner points	Value of Z = 7x + 4y
0(0,0)	Z = 0+ 0= 0
4(3,0)	Z = 7×3+0 = 21
8(2,3)	Z =7×2+4×3 = 26 (maximum)
C(0,6)	Z =7×0+ 4×6 = 24

Hence, for maximum profit, manufacturer produce 2 units of product A and 3 units of product B.

Question 12.
A machine costs a company ₹ 52000 and its effective life is estimated to be 25 yr. A sinking fund is created for replacing the machine by a new model at the end of its life time, when its scrap realizes a sum of ₹ 2500 only. The price of the new model is estimated to be 25% more than the price of present one. Find what amount should be set aside at the end of each year out of the profit for the sinking fund, if it accumulates at 3.5% compound annually? [given (1.035)²⁵ = 23632]
Answer:
Let ₹ R be the amount set aside each year. Since, the cost of new machine is 25% more than the cost of present.
Cost of machine = ₹ 52000
Cost of new machine after increasing the 25% of the cost of machine,
i.e. 52000 + 25% of 52000
= 52000 \(\left(1+\frac{25}{100}\right)\)
= 52000 × \(\frac{5}{4}\) = ₹ 65000
Scrap value of the present machine = ₹ 2500
So, net amount required at the end of 25 yr to purchase the new model = ₹ (65000 – 2500)
= ₹ 62500
We know that, R = \(\frac{i \times S}{(1+i)^{n}-1}\)
Here, S = ₹ 62500, n = 25 yr and i = \(\frac{3.5}{100}\) = 0.035

Thus, ₹ 1604.68 are set aside each year out of the profit to purchase the new model of the machine.

Question 13.
A bond of face value of ₹ 1000 matures in 5 yr. Interest is paid semi-annually and bond is priced to yield 8% per annum. If the present value of bond is ₹ 1100, find the annual coupon rate, [given (1.04)^-10 = 0.6761]
Or
A person buys a house for which be agrees to pay ₹ 25000 at the end of each month for 8 yr. If money is worth 12% converted monthly, what is the cash price of house? [given (1.01)^-96 = 0.3847]
Answer:
Let the annual coupon rate is 6%.
Given, F = ₹ 1000, then C = ₹ 1000 × \(\frac{r}{200}\) = ₹ 5 r
d = 8% per annum or 4% per half-year
i = \(\frac{4}{100}\) = 0.04
N = 5 × 2 = 10 yr and PV = ₹ 1100
∴ PV = \(\frac{C\left[1-(1+i)^{-N}\right]}{i}\) + F(1 + i)^-N

Hence, coupon rate is 10.47%.
Or
Given, EMI = ₹ 25000, n = 12 × 8 = 96 and
i = \(\frac{12}{1200}\) = 0.01
Let P be the cash price of house.

Hence, the cash price of house is ₹ 1538250.

Case Based/Data Based

Question 14.
Suppose the height and radius of cylindrical pot be 10 cm and ‘r’ cm. The volume of a cylindrical pot changes at a constant rate. At initial time, the radius of the pot is 3 cm. On the basis of above information, answer the following questions.
(i) Write the solution of differential equation formed by the given statement.
Answer:
According to the given statement,
\(\frac{d}{d t}\) (volume of cylinder) = k,
where k is some positive constant.
\(\frac{d}{d t}\) (πr²h) = k
⇒ \(\frac{d}{d t}\) [πr²(10)] = k [∵ h = 10 cm given]
⇒ 10π dr² = kdt
On integrating both sides, we get
10π ∫d(r²) = k∫dt
⇒ 10π(r²) = k(0) + C …(i)
Initially at t = 0, r = 3, then
10π(3)² = k(0) + C
⇒ C = 90π
Put C = 907t in Eq. (i), we get
10πr² = kt + 90π

(ii) After 5 s, the radius of pot becomes 6 cm. Then, find the value of constant.
Answer:
When t = 5 s, r = 6 cm, then
10π(6)² = k( 5) + 90π [∵ 10πr² = kt + 90π]
⇒ 5k= 360π – 90π
⇒ 5 k = 270π
⇒ k = 54π