CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 9 with Solutions

Students can access the CBSE Sample Papers for Class 12 Applied Mathematics with Solutions and marking scheme Term 2 Set 9 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Applied Mathematics Term 2 Set 9 with Solutions

Maximum Marks : 40
Time : 2 Hours

Instructions:

• The question paper is divided into 3 sections-A, B and C
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions. It contains one case study based question. Internal choice has been provided in one question.

Section – A [12 Marks]

Question 1.
Evaluate ∫\(\frac{1}{x^{2}\left(x^{4}+1\right)^{3 / 4}}\) dx
Or
The supply function for a commodity is p = 7 + x. Determine producer’s surplus, if 15 units of goods are sold.
Answer:

Or
Given, p = 7 + x and x₀ = 15
When x₀ = 15, then p₀ = 7 + 15 = 22

Question 2.
Find the f-test value for the following two samples from a populations

Or
Out of 250 clusters 10 clusters are selected randomly as given below:

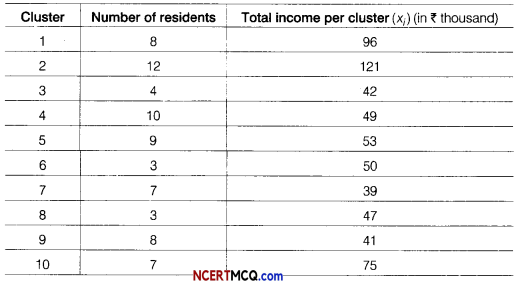
Estimate the population mean.
Answer:
We have, x̄ = \(\frac{5+7+4+9}{4}=\frac{25}{4}\) = 6.25
and ȳ = \(\frac{4+3+2+8}{4}=\frac{17}{4}\) = 4.25
Σ(x – x̄)² = (5 – 6.25)² + (7 – 6.25)² + (4 – 6.25)² + (9 – 6.25)²
= 1.5625 + 0.5625 + 5.0625 + 7.5625 = 14.75
and Σ(y – ȳ)² = (4 – 4.25)² + (3 – 4.25)² + (2 – 4.25)² + (8 – 4.25)²
= 0.0625 + 1.5625 + 5.0625 + 14.0625
= 20.75

We know that

Or

From the above table,
Σx_i = 96 + 121 + 42 + 49 + 53 + 50 + 39 + 47 + 41 + 75 = 613
and Σx_i = 8 + 12 + 4 + 10 + 9 + 3 + 7 + 3 + 8 + 7 = 71
∴ Population (x) = \(\frac{\Sigma x_{i}}{\Sigma n_{i}}=\frac{613}{71}\) = 8.63

Question 3.
Find the present value of perpetuity of ₹ 800 at the end of each quarter, if money is worth 10% compounded quarterly.
Answer:
Given, R = 800 and r = 10% = 0.10
∴ i = \(\frac{0.10}{4}\) = 0.025
∴ Present value of perpetuity,
P = \(\frac{R}{i}=\frac{800}{0.025}\) = ₹ 32000

Question 4.
The demand of a product over 6 weeks is 90, 110, 105, 130, 85 and 102. If 3 months moving average is x and 5 month morving average is y, find x + y.
Answer:
We know that
3 months moving average
= \(=\frac{\text { Sum of latest } 3 \text { trend }}{3}\)
and similarly for 5 months moving average
Now, x = \(\frac{130+85+102}{3}=\frac{317}{3}\) = 10567
and y = \(\frac{110+105+130+85+102}{5}=\frac{532}{5}\) = 1069
∴ x + y = 105.67 + 106.4 = 212.07

Question 5.
Find the effective rate, which is equivalent to a stated rate of 5% compounded semi-annually.
Answer:
Given, r = 5% and p = 2 (half-year)
So, effective rate (per rupee)
= (1 + \(\frac{r}{100 p}\))^p – 1
= (1 + \(\frac{5}{200}\))² – 1
= (1 + 0.025)² – 1
= (1.025)² – 1
= 1.0506 – 1
= 0.0506
∴ The effective rate = (0.0506) × 100% = 5.06%

Question 6.
Maximise Z = x + y, subject to constraints are
x + 4y ≤8, 2x + 3y ≤ 12, 3x + y ≤ 9 and x, y ≥ 0.
Answer:
Here, the given LPP is,

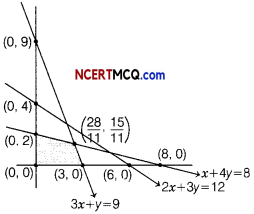
Maximise Z = x + y
Subject to constraints are,
x + 4y ≤8, 2x + 3y ≤ 12, 3x + y ≤ 9 and x, y ≥ 0
On solving x + 4y = 8 and 3x + y = 9, we get
x = \(\frac{28}{11}\) and y = \(\frac{15}{11}\)
From the feasible region, it is clear that coordinates of comer points are (0, 0), (3, 0), \(\left(\frac{28}{11}, \frac{15}{11}\right)\) and (0,2).

Corner points	Value of Z = x + y
(0,0)	0
(3,0)	3
\( \left(\frac{28}{11}, \frac{15}{11}\right) \)	\( \frac{43}{11}=3 \frac{10}{11} \)(maximum)
(0, 2)	2

Hence, the maximum value is 3 \(\frac{10}{11}\) at \(\left(\frac{28}{11}, \frac{5}{11}\right)\)

Section – B [12 Marks]

Question 7.
The population of a town grows at the rate of 10% per year. Using differential equation, find how long it will take for the population to grow 2 times.
Or
The marginal revenue function for a commodity is given by MR = 8 + 3x – 5x². Find the demand function.
Answer:
Let P0 be the population initially and P be the population after t yr.

According to question,
\(\frac{d}{d t}\)(P) = 10% of P ⇒ \(\frac{d P}{d t}=\frac{1}{10}\) P
⇒ \(\frac{1}{P}\) dP = \(\frac{1}{10}\)dt

On integration both sides, we get
∫\(\frac{1}{P}\) dP = ∫\(\frac{1}{10}\)dt
⇒ log P = \(\frac{1}{10}\)t + C

When t = 0, then P = P₀
∴ logP₀ = 0 + C ⇒ C = log P₀

From Eq.(i)
log P = \(\frac{1}{10}\)t + log P₀
⇒ log\(\frac{P}{P_{0}}=\frac{1}{10}\)t ……….(ii)

When the population grows 2 times, then
P = 2P₀
∴ log\(\left(\frac{2 P_{0}}{P_{0}}\right)=\frac{1}{10}\)t
⇒ t = 10log2
Hence, it takes 10 log 2 yr for the population to grow 2 times.

Or

Given MR = 8 + 3x – 5x²

Question 8.
10 students are selected at random from a college and their heights are found to be 100, 104,108,110,118,120,122,124,126 and 128 cm. In the light of these data, discuss the suggestion that the mean height of the students of the college is 110 cm. [given, t₉ (0.05) = 2.262].
Answer:
Consider, table for the sample mean (x̄) and S. Computation of x̄ and S

We have, \(\sum_{i=1}^{10}\) x_i = 1160 and n= 10
= \(\frac{1}{n} \sum_{i=1}^{10}\)x_i
= \(\frac{1160}{10}\) = 116

From the table, we find that

We have degree of freedom = (10 -1) = 9 It is given that t₉(0.05) = 2.262
∴ Calculated |t| = 1.94 < 2.262 = t₉(005)
i.e. Calculated |t| < tabulated t₉(0.05)
So, we accept the null hypothesis. Hence, the sample mean is same as the population mean. Consequently, the mean height of the students of the college is 110 cm.

Question 9.
From the following data compute 4-yearly moving averages and determine the trend values. Also, find the short-term fluctuations.

Answer:
Table for 4-yearly moving averages.

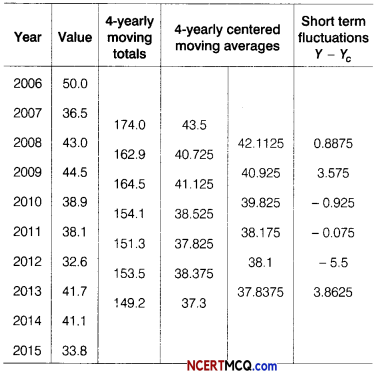
Question 10.
Mr. Kapoor invested ₹ 25000 in a mutual fund in year 2012. The value of mutual fund increased to ₹ 30000 in year 2016. Calculate the compound annual growth rate (CAGR) of his investment. [given, (1.2)^1/4 = 1.0466]
Answer:
Given, 13V = ₹ 25000, EV = ₹ 30000
and number of year (n) =4 yr
∴ CAGR = \(\left(\frac{\mathrm{EV}}{\mathrm{BV}}\right)^{1 / n}\) – 1
= \(\left(\frac{30000}{25000}\right)^{1 / 4}\) – 1 = \(\left(\frac{6}{5}\right)^{1 / 4}\) – 1
= (1.2)^1/4 – 1 = 1.0466 – 1 = 0.0466
∴ CAGR = (00466 × 100)% = 4.66%

Section – C [16 Marks]

Question 11.
Maximise and minimise Z = 3x – 4y, subject to constraints are
x – 2y ≤ 0, -3x + y ≤ 4, x – y ≤ 6 and x, y ≥ 0.
Answer:
Given, LPP is,
Maximise and minimise Z = 3x – 4y

Subject to constraints are
x – 2y ≤ 0, -3x + y ≤ 4, x – y ≤ 6 and x, y ≥ 0.
[on solving x – y = 6 and x – 2y = 0, we get x = 12 and y = 6]

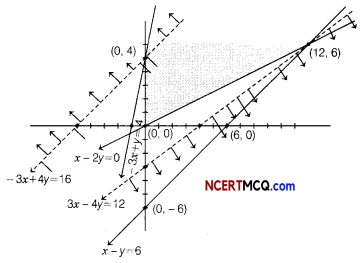
From the shown graph, for the feasible region, we see that it is unbounded and coordinates of comer points are (0, 0), (12, 6) and (0, 4).

Corner points	Value of Z = 3x – 4y
(0.0)	0
(0,4)	-16 (minimum)
(12,6)	12 (maximum)

For given unbounded region the minimum value of Z may or may not be -16. So, for deciding this, we graph the inequality.
3x – 4y < -16 and check whether the resulting open half plane has common points with feasible region or not. Thus, from the figure it shows it has common points with feasible region, so it does not have any minimum value. Also, similarly for maximum value, we graph the inequality 3x – 4y > 12 and see that resulting open half plane has no common points with the feasible region and hence maximum value 12 exist for Z = 3x – 4y.

Question 12.
A couple wishes to purchase a house for ₹ 1000000 with a down payment of ₹ 200000. If they can amortize the balance at an interest rate 8% per annum compounded monthly for 10 yr. Find the monthly installment (EMI). [given, (1.006)^-120 = 0.4878]
Answer:
Amortized amount, P = Cost of house – Cash down payment
= 1000000 – 200000 = ₹ 800000
i = \(\frac{0.08}{12}\) = 0.006
n = 10 × 12 = 120 months

Question 13.
Mr. Shiv Chandra wants to know the amount, he should pay for a goldmine expected to yield an annual return of 400000 for the next 10 yr, after which it will be worthless. Find the amount, he should pay for the mine, if he wants to yield 18% annual return on his investment and also set up a sinking fund to replace the purchase price. Assume that the sinking fund earns 10% annually. [given (1.1)¹⁰ = 2.5937]
Or
A bond has a face value of ₹ 1000, matures in 4 yr coupon rate is 4% per annum. The bond makes annual payments. If the yield to maturity is 4%. Find the fair value of bond, [given (1.04)^-4 =0.8551]
Answer:
Given, rate of return on investment = 18% = 0.18
Let x be the purchase price of the mine.
Return on investment of ₹ x per year = 0.18+
Life of mine (n) = 10 yr
Net annual return = ₹ 400000

Sinking fund is created to replace the purchase price.
∴ Amount to be placed into sinking fund each year is ₹ (400000 – 0.18x).
These payments must accumulate to ₹ x at the end of 10 yr.
∴ Amount A = ₹ x,
i = r = 10% = 0.10
Here, n = 10 and R = ₹ (400000 – 0.18.x)

We know that

∴ Purchase price of the goldmine is ₹ 1648125.25

Or

Here, F = ₹ 1000, r = 4%, N = 4 yr and d = 4%

Case Based/Data Based

Question 14.
A long lasting company produces biscuits. Whose marginal revenue functions of a commodity is given by MR = 6x² – 5x + 2.

On the basis of the above information, answer the following questions.
(i) Find the total revenue functions.
Answer:
Given, marginal revenue functions
MR = 6x² – 5x + 2
⇒ \(\frac{d R}{d x}\) = MR = 6x² – 5x + 2
R = ∫(6x² – 5x + 2)dx
R = \(\frac{6 x^{3}}{3}-\frac{5 x^{2}}{2}\) + 2x + K
R = 2x³ – \(\frac{5 x^{2}}{2}\) + 2x + K

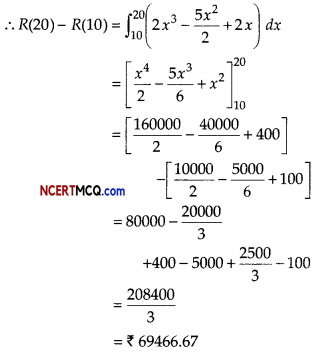
(ii) If the productions increases from 10 to 20. Find the increase in their revenue.
Answer:
The increase in revenue, when productions increase from 10 to 20, is