CBSE Sample Papers for Class 12 Maths Paper 1

CBSE Sample Papers for Class 12 Maths Paper 1 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 1.

CBSE Sample Papers for Class 12 Maths Paper 1

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 1
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 1 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.

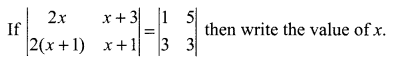
Question 2.
Check the continuity of the function

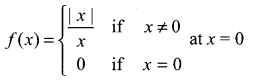
Question 3.
Integrate

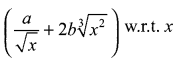
Question 4.
Find a vector in the direction of vector \(\vec { a } =2\hat { i } -3\hat { j } +4\hat { k }\) that has magnitude 5 units.

SECTION B

Question 5.
Find the value of x + y + z if

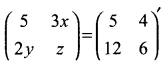
Question 6.
Differentiate log (1 + θ) with respect to sin^-1 θ.

Question 7.
A balloon which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the radius is 10 cm.

Question 8.
Show that the function f(x) = tan x – x is always increasing in X ∈ R.

Question 9.
Find the equation of the plane passing through the point (1, 4, -2) and it is parallel to the plane -2x + y + 3z = 0.

Question 10.
Event E and F are such that P (not E or not F) = 0.25. State whether E and F are mutually exclusive.

Question 11.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of ₹ 80 on each type of A and ₹ 120 on each type of B. Formulate it as L.P.P. to make a maximum profit.

Question 12.
Evaluate

SECTION C

Question 13.
Prove that

Question 14.
Using properties of determinant prove that

OR
Using properties of determinant prove that

Question 15.

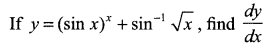
Question 16.
Evaluate

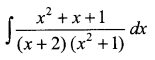
Question 17.
Evaluate

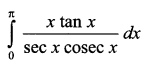
OR
Evaluate

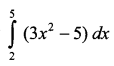
as limit of sums

Question 18.
Solve the differential equation

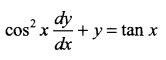
Question 19.

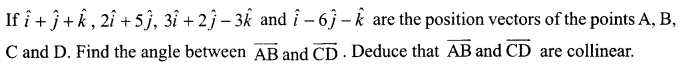
Question 20.

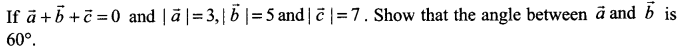
Question 21.
On a multiple choice examination with three possible answers (out of which only one is correct) for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing? Is examination necessary for success in the life of student?

Question 22.
There are two bags, bag I and bag II. Bag I contains 4 white and 3 red balls while another bag II contains 3 white and 7 red balls. One ball in drawn at random from one of the bags and it is found to be white. Find the probability that it was drawn from bag I.

Question 23.
Solve the following L.P.P.
Maximize profit Z = 17.5 x + 7y
Subject to constraints are x + 3y ≤ 12 3x + y ≤ 12, x, y ≥ 0

SECTION D

Question 24.
If \(A=\left( \begin{matrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{matrix} \right)\) Find A-1 and hence solve the system of equations
x + 2y + z = 4
-x + y + z = 0
x – 3y + z = 2

Question 25.
Let x be non-empty set. P(x) be its power set. Let * be an operation defined on element of P(x) by,
A*B = A ∩ B \(\forall\) A, B ∈ P(x). Then
(i) Prove that * is a binary operation in P(x)
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity element in P(x) w.r.t. *
(v) Find all the invertible elements of P(x)
(vi) If o is another binary operation defined on P(x) as AοB = A ∪ B then verify that o distributes itself over *
OR
Consider f : R₊ → [-5, ∞) given by f(x) = 9x² + 6x – 5. Show that f is invertible. Find the inverse of f.

Question 26.
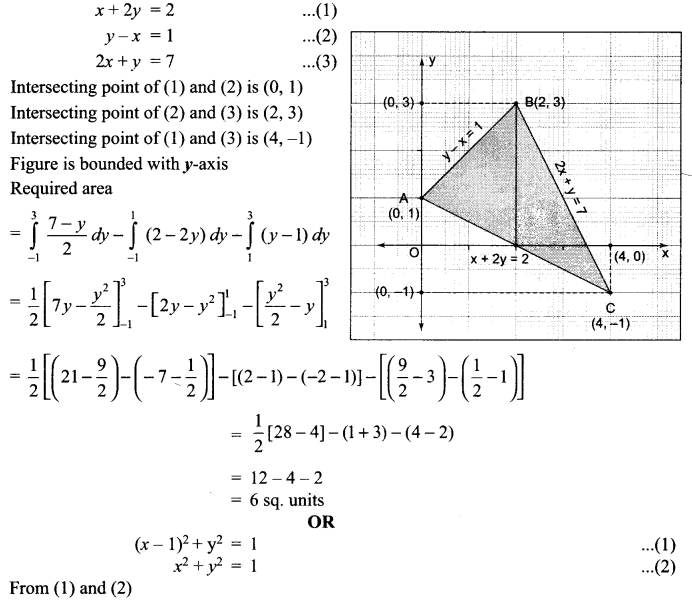
Using integration find the area bounded by the lines x + 2y = 2, y – x = 1, 2x + y = 7.
OR
Using integration find the area bounded by the curves (x – 1)² + y² = 1 and x² + y² = 1

Question 27.
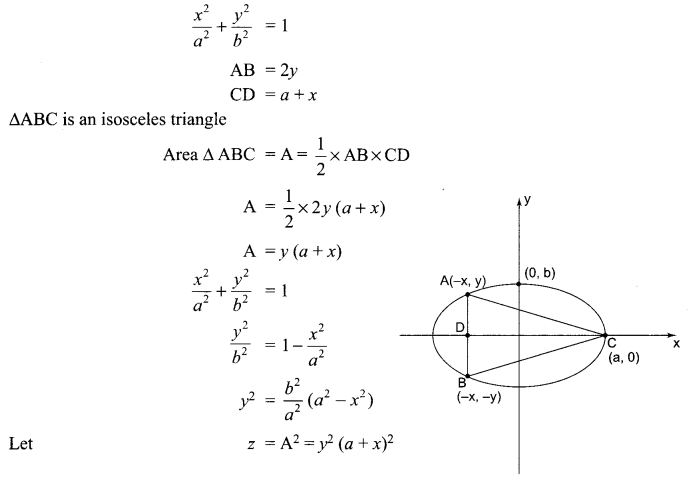
Find the maximum area of the isosceles triangle inscribed in the ellipse \(\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1\) with its vertex at one end of major axis.

Question 28.
Solve the following differential equation:

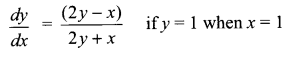
Question 29.
Find the equation of plane passing through the point (-1, -1, 2) and perpendicular to each of the following planes:
2x + 3y – 3z = 2 and 5x – 4y + z = 6
OR
Find the equation of the plane passing through the points (3, 4, 1) and (0, 1, 0) and parallel to the line \(\frac { x+3 }{ 2 } +\frac { y-3 }{ 7 } +\frac { z-2 }{ 5 }\)

Solutions

Solution 1.

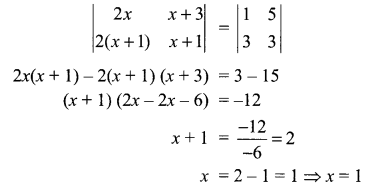
Solution 2.

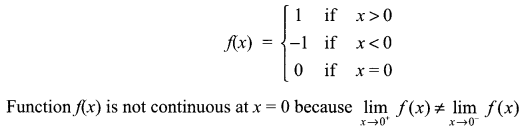
Solution 3.

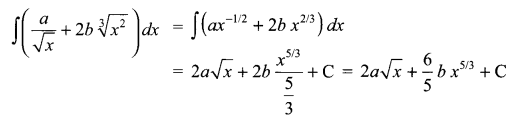
Solution 4.

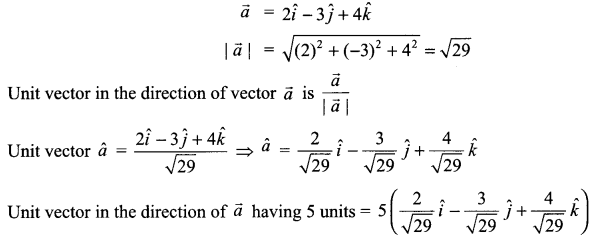
Solution 5.

Solution 6.

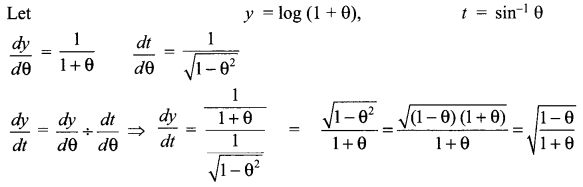
Solution 7.

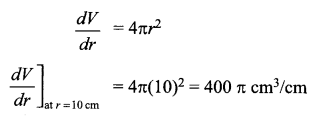
Solution 8.
f(x) = tan x – x
f'(x) = sec²x – 1
\(\forall\) x ∈ R, The range of sec² x is [1, ∞)
So for all x ∈ R, f'(x) ≥ 0
Hence f(x) is always increasing function.

Solution 9.
Equation of plane passing through the point (1, 4, -2) is a(x – 1) + b(y – 4) + c (z + 2) = 0 …… (i)
where a, b, c are direction ratio of plane.
Plane (i) is parallel to the plane -2x + y + 3z = 0, so direction ratio of both planes will be in ratio

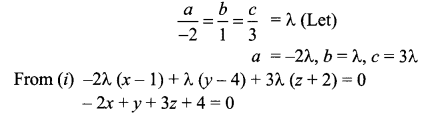
Solution 10.
P(not E or not F) = 0.25 or P(E’ ∪ F’) = 0.25
P(E ∩ F)’ = 0.25
P(E ∩ F)’ = 1 – P(E ∩ F)
0.25 = 1 – P (E ∩ F)
P(E ∩ F) = 1 – 0.25 = 0.75 ≠ 0
So E and F are not mutually exclusive.

Solution 11.
Let x teaching aids of type A andy teaching aids of type B are manufactured.
Objective function is maximize profit Z = ₹ (80x + 120y)
Subject to constraints are
9x + 12y ≤ 180 (fabricating constraint)
x + 3y ≤ 30 (finishing constraint)
x, y ≥ 0 (non-negative constraint)

Solution 12.

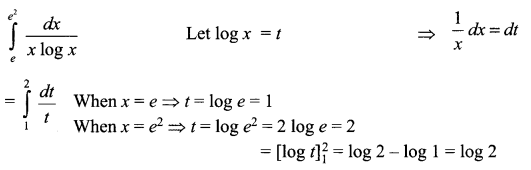
Solution 13.

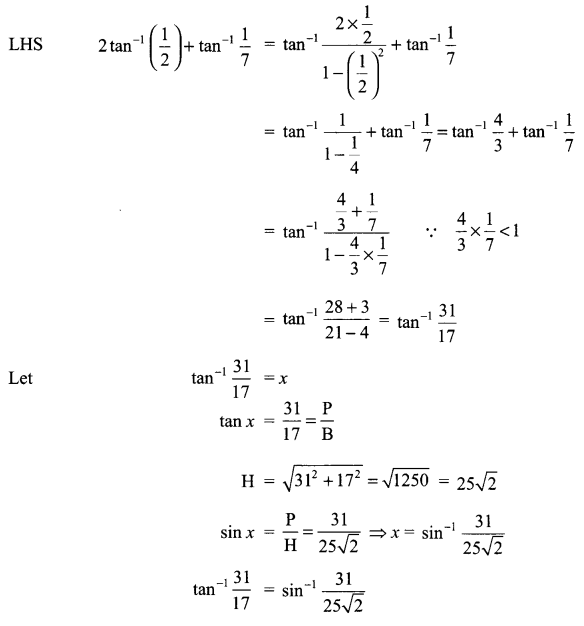
Solution 14.

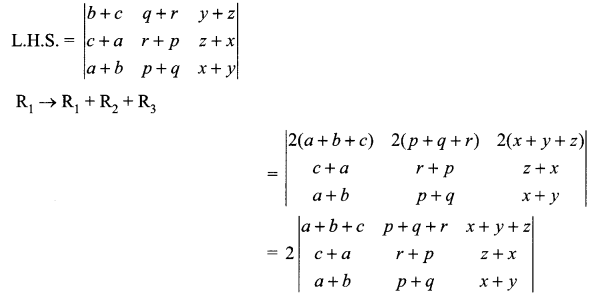
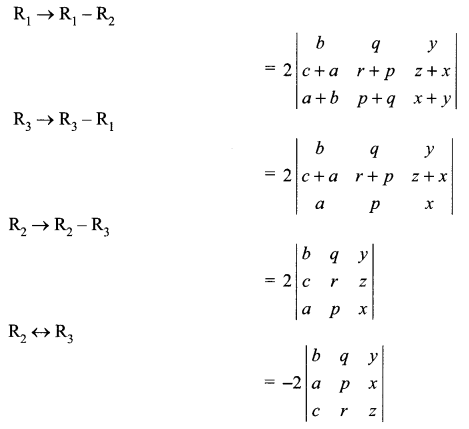
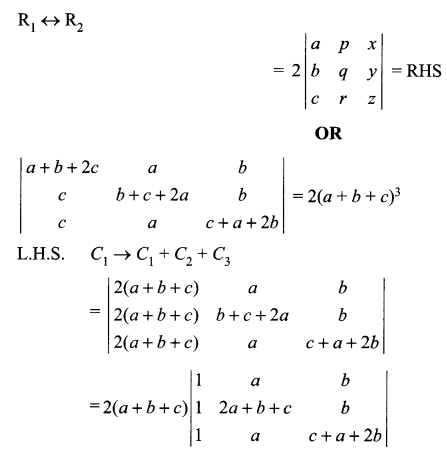
Solution 15.

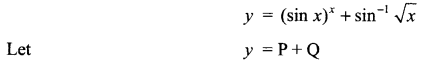
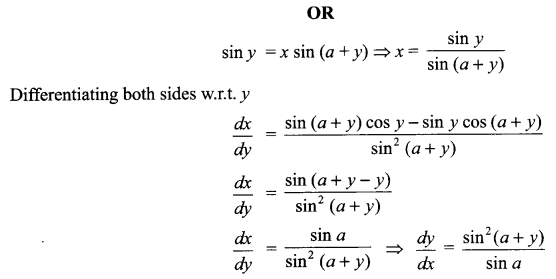
Solution 16.

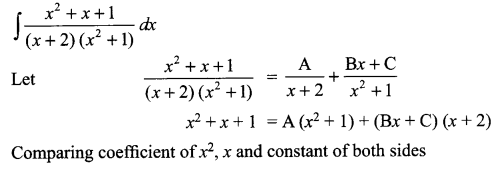
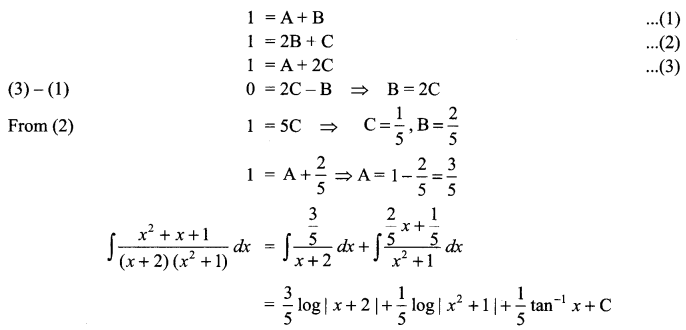
Solution 17.

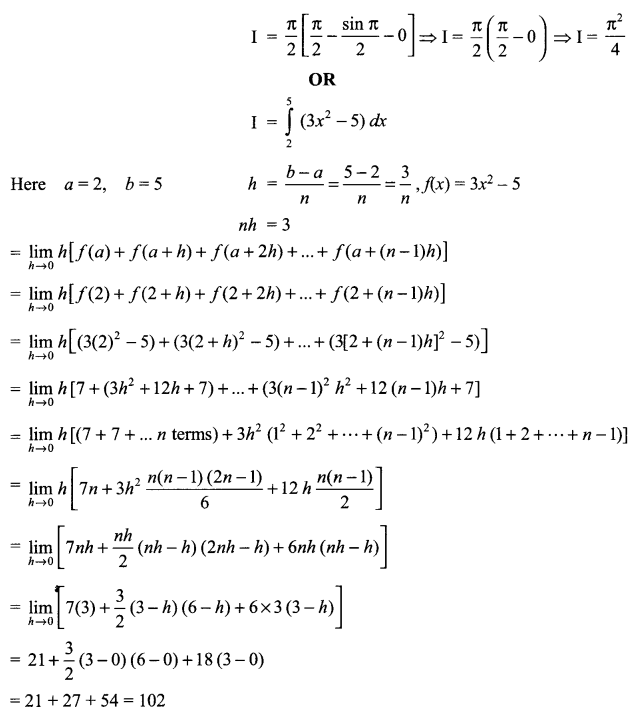
Solution 18.

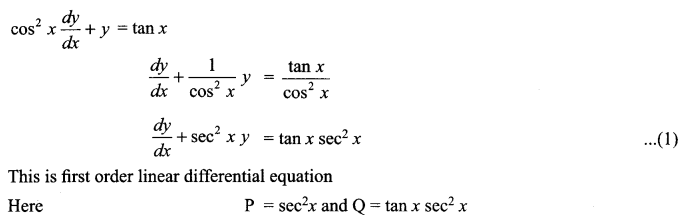
Solution 19.

Solution 20.

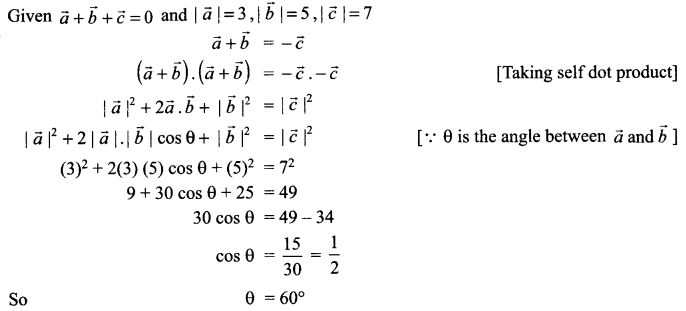
Solution 21.
Total questions = n = 5

Yes. In the life of students examination are necessary. By this, student keep his/her knowledge up-to-date.

Solution 22.
E₁ is the event. Bag I is selected.
E₂ is the event. Bag II is selected.

Solution 23.

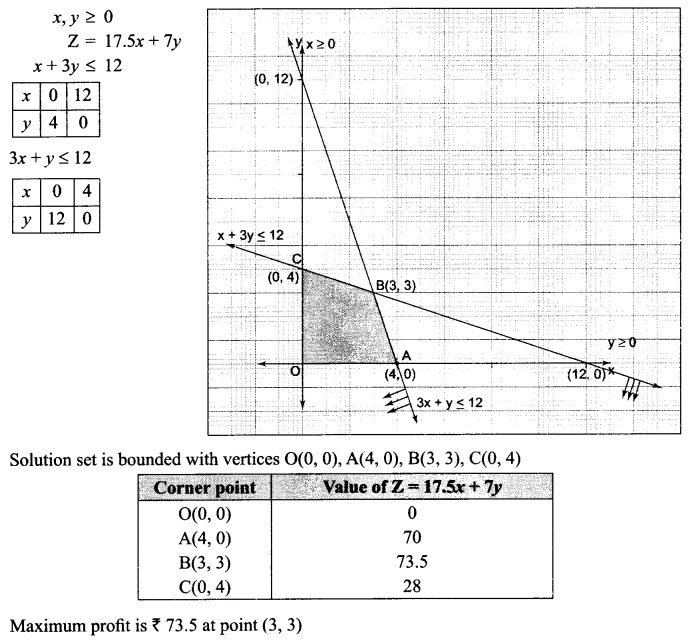
Solution 24.

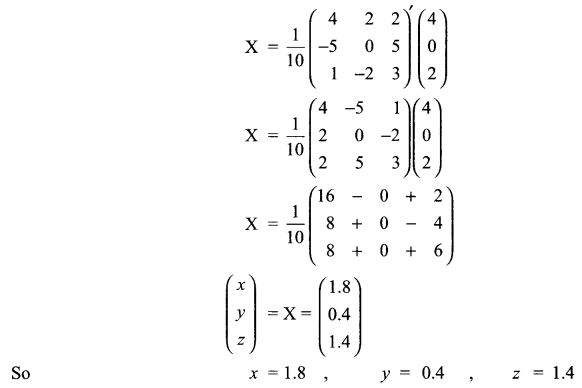
Solution 25.




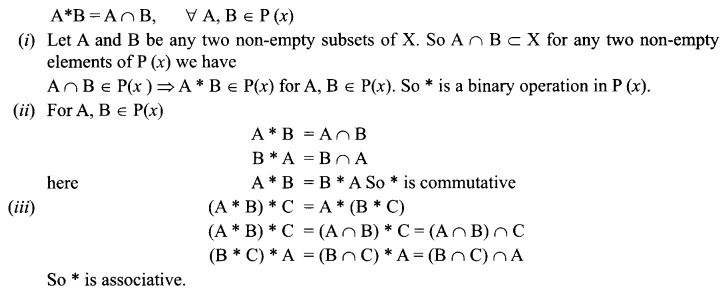
Solution 26.

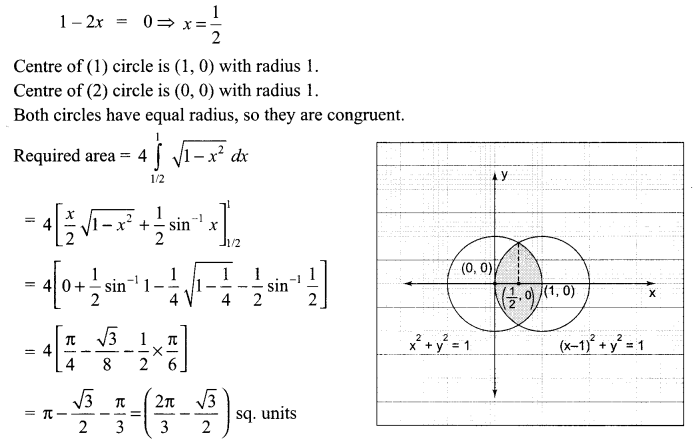
Solution 27.

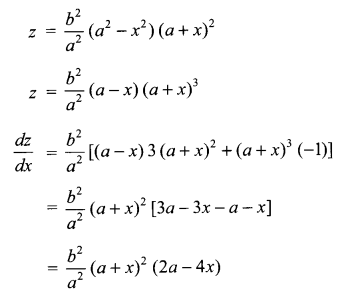
Solution 28.

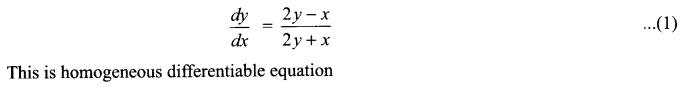
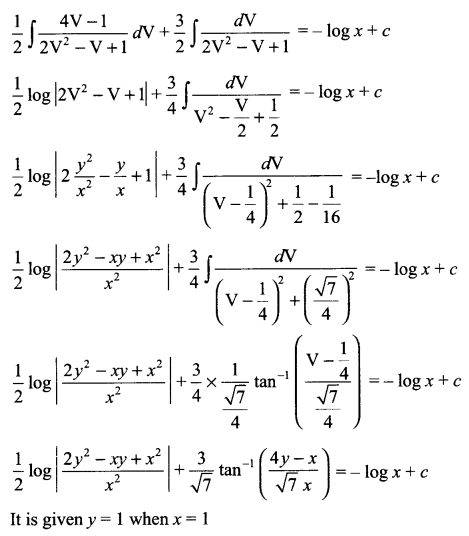
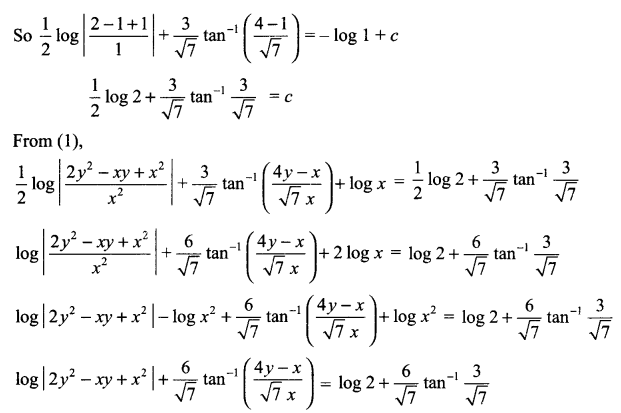
Solution 29.
Equation of plane passing through the point (-1, -1, 2) is
a (x + 1) + b (y + 1) + c (z – 2) = 0 …(1)
Here a, b, c are direction ratio of this plane.
Plane (1) is perpendicular to the planes
2x + 3y – 3z =2 and
5x – 4y + z = 6 so
2a + 3b – 3c = 0
5a – 4b + c = 0

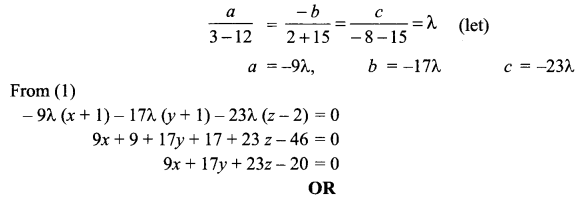
We hope the CBSE Sample Papers for Class 12 Maths Paper 1 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 1, drop a comment below and we will get back to you at the earliest.