CBSE Sample Papers for Class 12 Maths Paper 2

CBSE Sample Papers for Class 12 Maths Paper 2 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 2.

CBSE Sample Papers for Class 12 Maths Paper 2

Board	CBSE
Class	XII
Subject	Maths
Sample Paper Set	Paper 2
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 2 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 100

General Instructions:

• All questions are compulsory.
• Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
• Questions 5-12 in section B are short answer type questions carrying 2 marks each.
• Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
• Questions 24-29 in section D are long answer II type questions carrying 6 marks each.

SECTION A

Question 1.
Find λ when projection of \(\bar { a } =\lambda \hat { i } +\hat { j } +4\hat { k }\) on \(\bar { b } =2\hat { i } +6\hat { j } +3\hat { k }\) is 4 units.

Question 2.
Evaluate \(\int _{ 2 }^{ 3 }{ \frac { 1 }{ 2x } } dx\)

Question 3.
Write the cofactor of the element a₃₁ in \(A=\left( \begin{matrix} 3 & 2 & 6 \\ 5 & 0 & 7 \\ 3 & 8 & 5 \end{matrix} \right)\)

Question 4.
For which values of x, f(x) = \(\left| x-1 \right| +\left| x-2 \right|\) is not differentiable?

SECTION B

Question 5.
For what value of c, Mean Value theorem is applicable for the function f(x) = x + \(\frac { 1 }{ x }\) on [1, 3] ?

Question 6.
Find \(\frac { dy }{ dx }\), if y = \({ tan }^{ -1 }\left( \frac { 1-cosx }{ 1+cosx } \right)\)

Question 7.
For the matrix \(A=\begin{pmatrix} 3 & 1 \\ 7 & 5 \end{pmatrix}\) find the value of x and y so that A² + xI = yA

Question 8.
Using derivative, find the approximate percentage increase in the area of a circle if its radius is increased by 2%.

Question 9.
The random variable x has a probability distribution P(x) of the following form, where k is some number

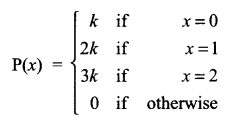
Find the value of (i) k (ii) P(x ≥ 2)

Question 10.
Find the equation of line passing through the point with position vector \(\hat { i } +\hat { j } +\hat { k }\) and perpendicular to the plane \(\left( 2\hat { i } +\hat { j } +\hat { 3k } \right) \cdot \hat { r } =5\) in both vector form and Cartesian form.

Question 11.
Evaluate \(\int _{ 0 }^{ 1 }{ x{ e }^{ { x }^{ 2 } } } dx\)

Question 12.
Anil wants to invest at most ₹ 12000 in bonds A and B. He wants to invest atleast ₹ 2000 in bond A and atleast ₹ 4000 in bond B. If rate of interest on bond A is 8% per annum and rate of interest on bond B is 9% per annum. Formulate it as L.P.P. to find maximum yearly income.

SECTION C

Question 13.
Two balls are drawn at random from a bag containing 2 white, 3 red, 5 green and 4 black balls one by one without replacement. Find the probability that both the balls are of different colours.

Question 14.
The probabilities of two students A and B coming to the school in time are \(\frac { 3 }{ 7 }\) and \(\frac { 5 }{ 7 }\) respectively. Assuming that the events A coming in time and B coming in time are independent. Find the probability of only one of them coming to the school in time. Write atleast one advantage of coming to the school in time.

Question 15.

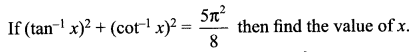
Question 16.

Question 17.

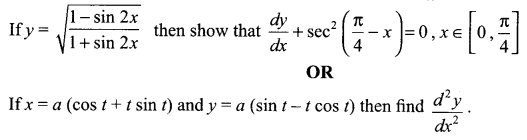
Question 18.
Evaluate \(\int { \frac { sin\phi d\phi }{ \sqrt { { sin }^{ 2 }\phi +2cos\phi +3 } } }\)

Question 19.
Evaluate \(\int _{ 0 }^{ \pi }{ \frac { x\quad tanx }{ secx+tanx } } dx\)
OR
Evaluate \(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ log\quad sinx\quad dx }\)

Question 20.

Question 21.
Find the particular solution for the differential equation

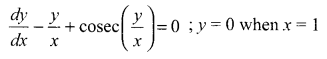
Question 22.
If the sum of two unit vectors is a unit vector, prove that the magnitude of their difference is √3.

Question 23.
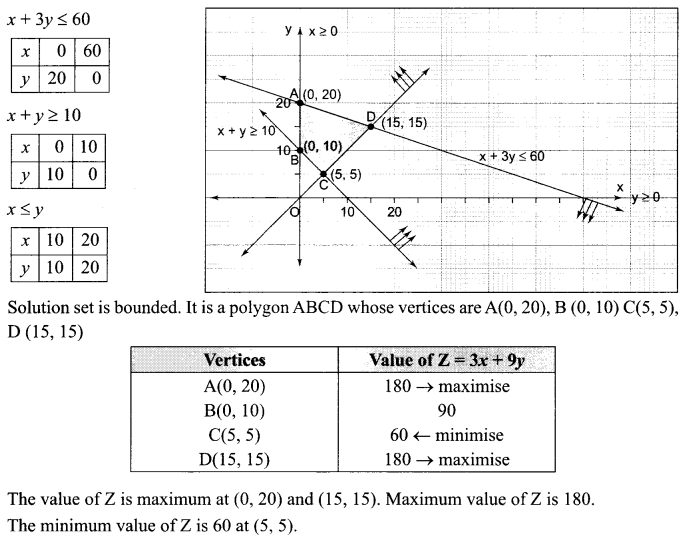
Solve the following L.P.P. graphically:
Minimize and maximize Z = 3x + 9y
Subject to constraint
x + 3y ≤ 60
x + y ≥ 10
x ≤ y
x, y ≥ 0

SECTION D

Question 24.
Find the distance of the point P(3, 4, 4) from the point where the line joining the points A (3, -4, -5) and B (2, -3, 1) intersect the plane 2x + y + z = 7.
OR
It lines \(\frac { x-1 }{ 1 } =\frac { y+1 }{ 3 } =\frac { z-1 }{ 4 }\) and \(\frac { x-3 }{ 1 } =\frac { y-k }{ 2 } =\frac { z }{ 1 }\) intersect, then find the value of k and hence find the equation of the plane containing these lines.

Question 25.
Let N denote the set of all natural numbers and R be the relation on N x N defined by (a, b) R (c, d) if ad (b + c) = bc (a + d)
Show that R is an equivalence relation.
OR
A binary operation * is defined on the set X = R – {-1} by x * y = x + y + xy ∀ x, y ∈ X. Check whether * is commutative and associative. Find the identity element and also find the inverse of each element of X.

Question 26.
Given the sum of the perimeter of a square and a circle. Show that sum of their areas is least when the side of the square is equal to the diameter of the circle.
OR
Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \(\frac { 2R }{ \surd 3 }\). Also find the maximum volume.

Question 27.
Determine the product \(\left( \begin{matrix} -4 & 4 & 4 \\ -7 & 1 & 3 \\ 5 & -3 & -1 \end{matrix} \right) \left( \begin{matrix} 1 & -1 & 1 \\ 1 & -2 & -2 \\ 2 & 1 & 3 \end{matrix} \right)\) and use it to solve the system of equations
x – y + z = 4
x – 2y – 2z = 9
2x + y + 3z = 1

Question 28.
Find the area of the region {(x, y): x² + y² ≤ 4, x + y ≥ 2} using integration.

Question 29.
Solve the following differential equation

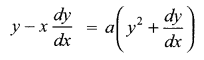
Solutions

Solution 1.

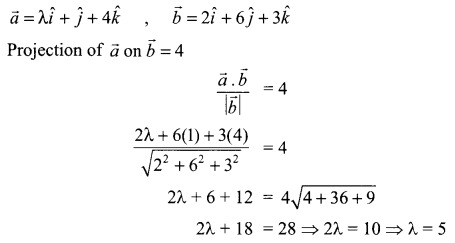
Solution 2.

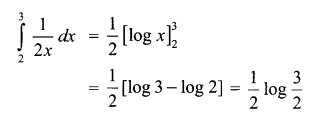
Solution 3.

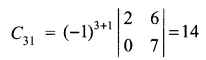
Solution 4.
At x = 1 and x = 2, f(x) is not differentiable.

Solution 5.

Solution 6.

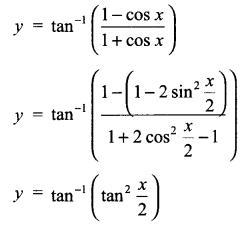
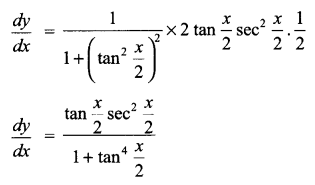
Solution 7.

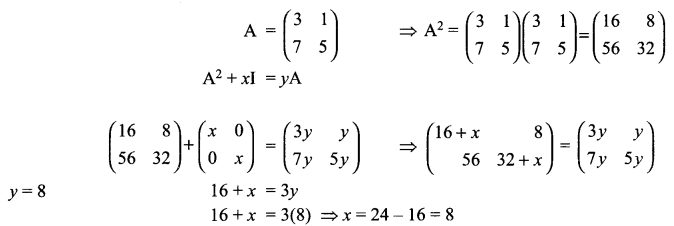
Solution 8.

Solution 9.

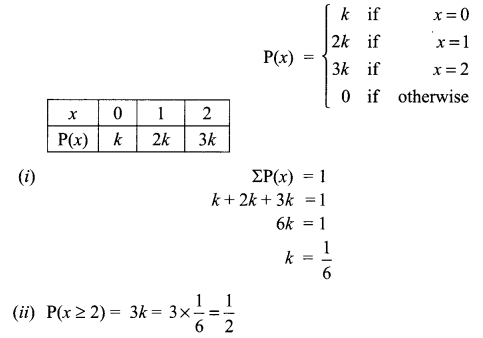
Solution 10.

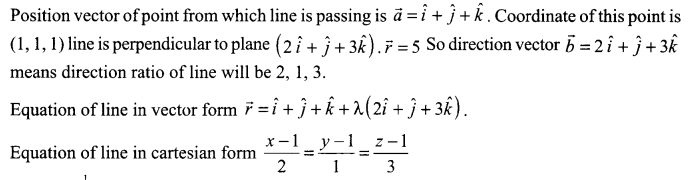
Solution 11.

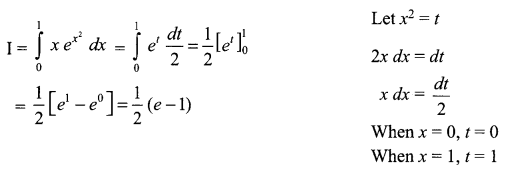
Solution 12.
Let amount invested in bond A is ₹ x, and amount invested in bond B is ₹ y.
Objective function is maximise income Z = \(\frac { 8x }{ 100 } +\frac { 9y }{ 100 }\)
Subject to constraints are
x + y ≤ 12000 (Investment constraint)
x ≥ 2000
y ≥ 4000

Solution 13.
Bag contains- 2 White balls, 3 Red balls, 5 Green balls, 4 Black balls
Total balls = 14
2 balls are drawn without replacement.
P (both balls are of different colours) = 1 – P(both balls are of same colour)
= 1 – [P(both white) + P (both red) + P (both green) + P (both black)]

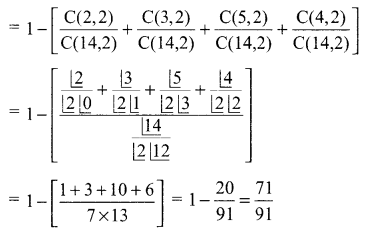
Solution 14.
Let E₁ is the event: A coming in time
and E₂ is the event: B coming in time

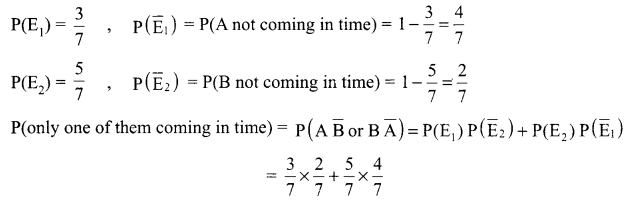
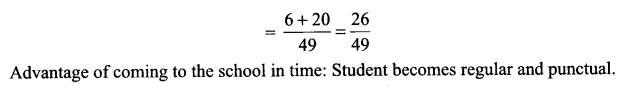
Solution 15.

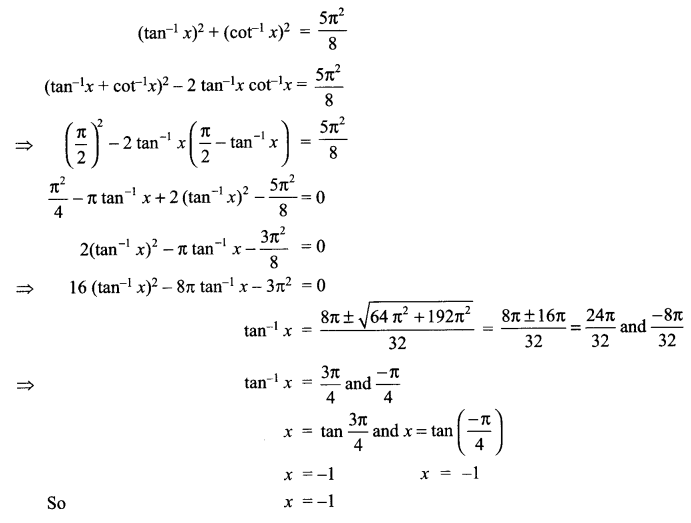
Solution 16.
Using elementary row transformation
A = IA

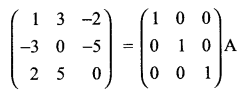
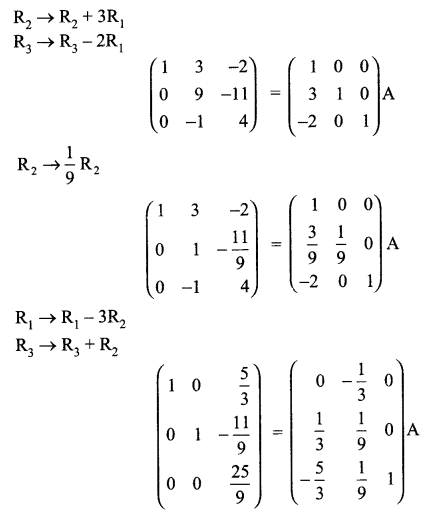
Solution 17.

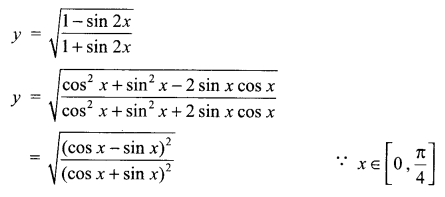
Solution 18.

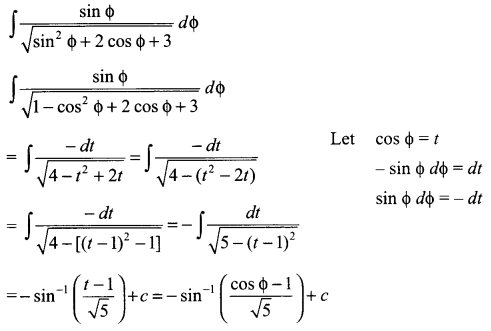
Solution 19.

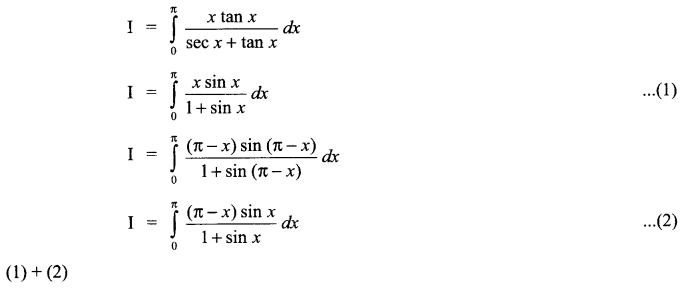
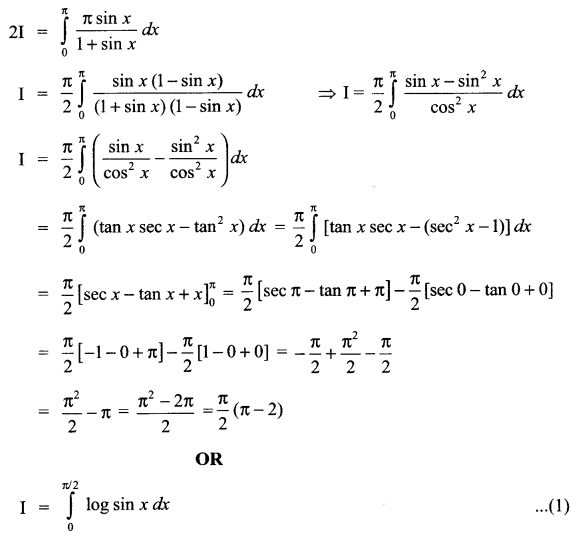
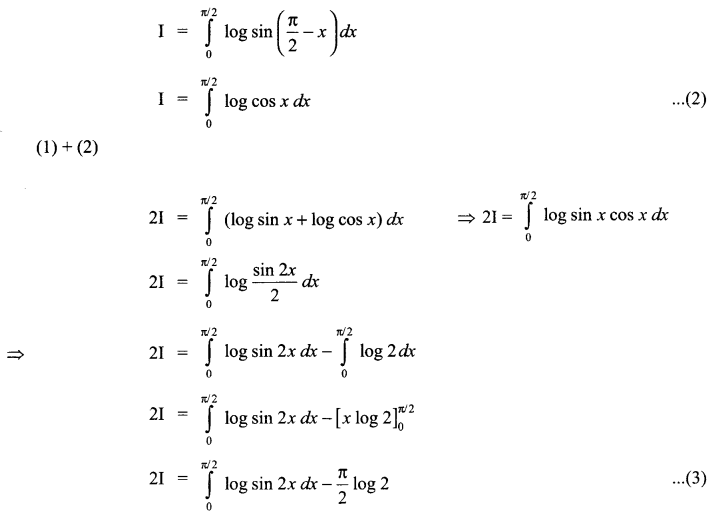
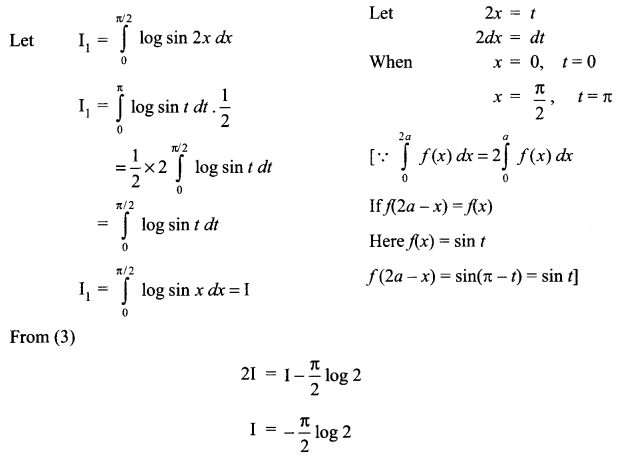
Solution 20.

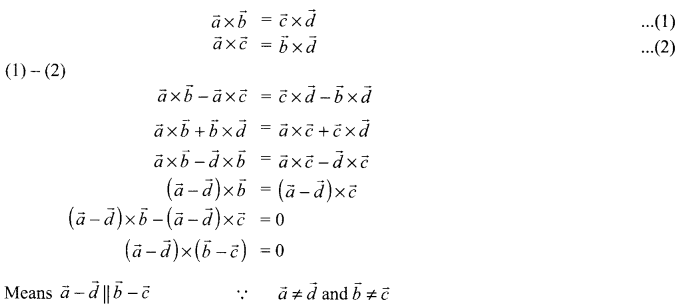
Solution 21.

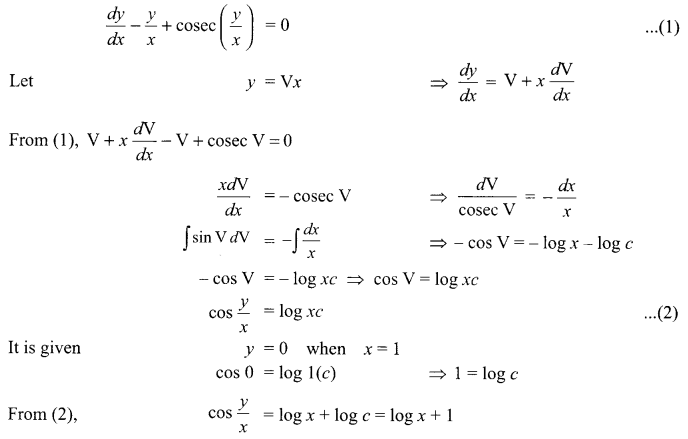
Solution 22.

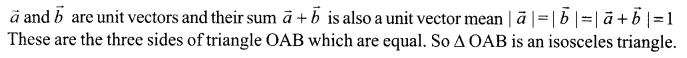
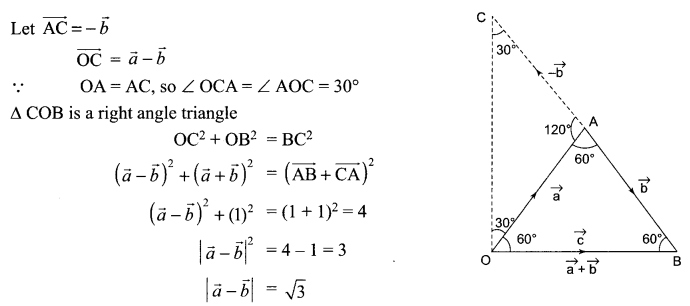
Solution 23.

Solution 24.
Equation of line joining the points A (3, -4, -5) and B (2, -3, 1) is

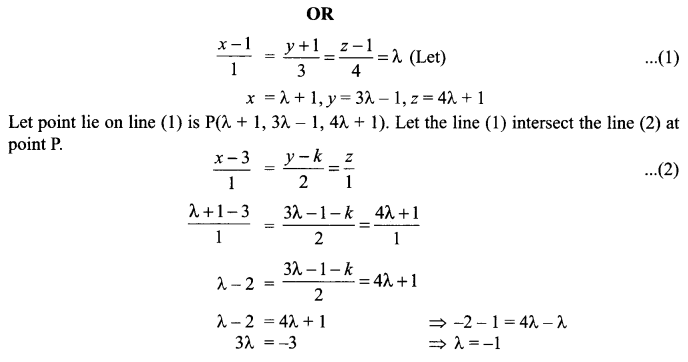
Solution 25.
R be a relation on N x N defined by
(a, b) R (c, d) if ad (b + c) = bc (a + d)

Solution 26.

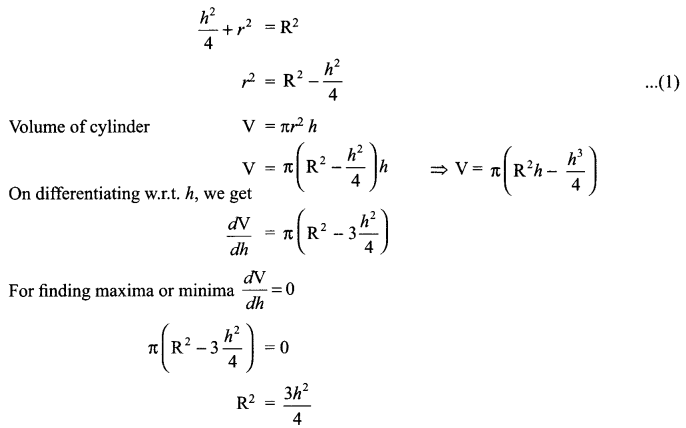
Solution 27.

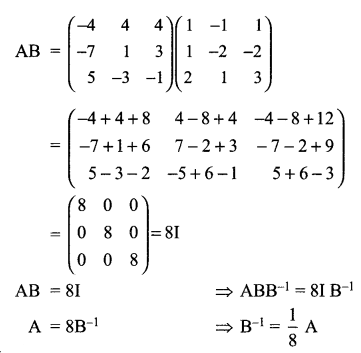
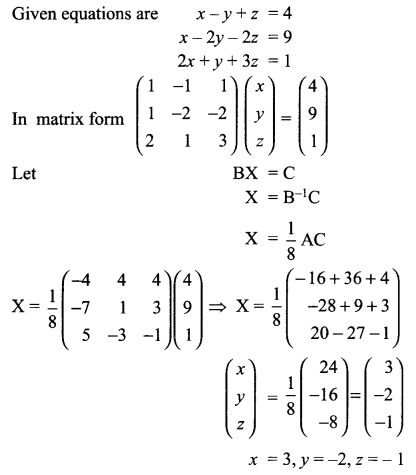
Solution 28.

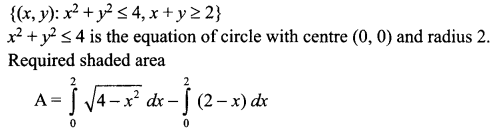
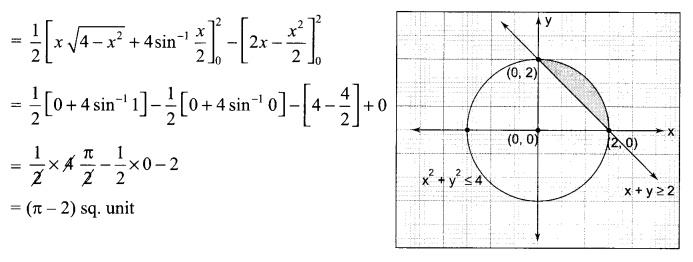
Solution 29.

We hope the CBSE Sample Papers for Class 12 Maths Paper 2 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 2, drop a comment below and we will get back to you at the earliest.