CBSE Sample Papers for Class 12 Maths Term 2 Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 1 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Find \(\int \frac{\log x}{(1+\log x)^{2}}\)dx
Find \(\int \frac{\sin 2 x}{\sqrt{9-\cos ^{4} x}}\)dx
Answer:

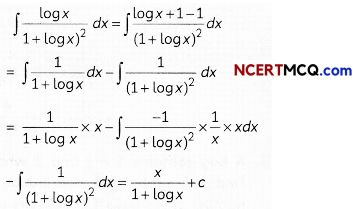
Explanation:
Let,
I = \(\int \frac{\log x}{(1+\log x)^{2}}\)dx

Caution:
The tricky part of the question lies where, one need to break the given integral into 2 parts, So into integrate it casing.
OR
Put cos² x = t ⇒ – 2 cos x sin x dx = dt ⇒ sin 2xdx = – dt
The given integral = – \(\int \frac{d t}{\sqrt{3^{2}-t^{2}}}\) = – sin^-1\(\) + c
= – sin^-1\(\frac{\cos ^{2} x}{3}\) + c

Question 2.
Write the sum of the order and the degree of the following differential equation:
\(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) = 5
Answer:
Order = 2, Degree = 1, Sum = 3
Explanation: given, differential equation is:
\(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) = 5
or \(\frac{d^{2} y}{d x^{2}}\) = 5
∴ order of D.E. = 2
Degree of D.E. = 1
∴ Required sum = 2 + 1 = 3

Concept Applied:
The order of a differential equation is defined as the highest order derviative it contains the degree of a differential equation is defined as the power to which highest order derivative is raised.

Question 3.
If â and b̂ are unit vectors, then prove that | â + b̂ | = 2 cos \(\frac{\theta}{2}\), where θ is the angle between them.
Answer:
(â + b̂).(â + b̂) = |â|² + |b̂|² + 2(â.b̂)
|â + b̂|² = 1 + 1 + 2 cos θ
= 2(1 + cos θ) = 4 cos² \(\frac{\theta}{2}\)
∴ |â + b̂| = 2 cos\(\frac{\theta}{2}\)

Explanation: Here, â and b̂are the unit vectors.
Dot product of |â + b̂.|â + b̂|
= |â|² + |b̂|² + 2(â – b̂)
But â and b̂ are unit vectors
∴ (â + b̂)² = 1 + 1 + 2 â. b̂ cos θ
⇒ (â + b̂)² = 2 + 2.1.1. cos θ
⇒ (â + b̂)² = 2(1 – cos θ)
⇒ (â + b̂)² = 2 × 2 cos²\(\frac{\theta}{2}\)
⇒ (â + b̂) = \(\sqrt{4 \cos ^{2} \frac{\theta}{2}}\)
⇒ |â + b̂| = 2 cos \(\frac{\theta}{2}\)
Hence proved.

Question 4.
Find the direction consines of the following line:
\(\frac{3-x}{-1}=\frac{2 y-1}{2}=\frac{z}{4}\)
Answer:
The given line is
\(\frac{x-3}{1}=\frac{y-\frac{1}{2}}{1}=\frac{z}{4}\)
Its direction ratios are (1, 1, 4).
Its direction consines are
\(\left(\frac{1}{3 \sqrt{2}}, \frac{1}{3 \sqrt{2}}, \frac{4}{3 \sqrt{2}}\right)\)

Explanation:
The given equation of line is:

Question 5.
A bag contains 1 red and 3 white balls. Find the probability distribution of the number of red balls if 2 balls are drawn at random from the bag one-by-one without replacement.
Answer:
Let X be the random variable defined as the number of red balls.
Then X = 0, 1
P(X = 0) = \(\frac{3}{4} \times \frac{2}{3}\) = \(\frac{6}{12}\) = \(\)
P(X = 1) = \(\frac{1}{4} \times \frac{3}{3}+\frac{3}{4} \times \frac{1}{3}\) = \(\frac{6}{12}\) = \(\frac{1}{2}\)

Probability Distribution Table:

x	0	1
P(X)	\(\frac{1}{2}\)	\(\frac{1}{2}\)

Explanation: Total number of balls in the bag = 4
Now, 2 balls are drawn from the bag one by one without replacement.
Let, X be the random variables defined as the number of red balls.
Then, X = 0, 1
P(X = 0) = \(\frac{3}{4} \times \frac{2}{3}\) = \(\frac{1}{3}\)
P(X = 1) = \(\frac{1}{4} \times \frac{3}{3}+\frac{3}{4} \times \frac{1}{3}\)
= \(\frac{6}{12}=\frac{1}{2}\)

x	0	1
P(X)	\(\frac{1}{2}\)	\(\frac{1}{2}\)

Caution:
As there is only 1 red ball in the bag, so in 2 draws we can get only 1 red balls at maximum.

Question 6.
Two cards are drawn at random from a pack of 52 cards one-by-one without replacement. What is the probability of getting first card red and second card Jack?
Answer:
The required probability = P((The first is a red jack card and The second is a jack card) or (The first is a red non-jack card and The second is a jack card))
= \(\frac{2}{52} \times \frac{3}{51}+\frac{24}{52} \times \frac{4}{51}\) = \(\frac{1}{26}\)

Explanation:
There are 52 cards in a pack of cards.
No. of red cards = 26
No. of pack = 4
∴ Required probability
= P(First card non-red jack, second card jack) + P(first cards red jack, second card jack)

SECTION – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Find: \(\int \frac{x+1}{\left(x^{2}+1\right)}\) dx
Answer:
Let \(\frac{x+1}{\left(x^{2}+1\right) x}\) = \(\frac{A x+B}{x^{2}+1}+\frac{C}{x}\) = \(\frac{(A x+B) x+C\left(x^{2}+1\right)}{\left(x^{2}+1\right) x}\)
⇒ x + 1 = (Ax + B)x + C(x² + 1) (An identity)
Equating the coeffcients, we get
B = 1, C = 1, A + C = 0
Hence, A = -1, B = 1, C = 1

Explanation:
Let,
I = \(\int \frac{x+1}{\left(x^{2}+1\right) x}\) dx
By partial fraction
Let
\(\frac{x+1}{\left(x^{2}+1\right) x}\) = \(\frac{A x+B}{x^{2}+1}+\frac{C}{x}\)
⇒ \(\frac{x+1}{\left(x^{2}+1\right) x}\) = \(\frac{(\mathrm{A} x+\mathrm{B}) x+\mathrm{C}\left(x^{2}+1\right)}{x\left(x^{2}+1\right)}\)
⇒ x + 1 = Ax² + Bx + Cx²+ C
⇒ x + 1 = (A + C) x² + Bx + C
on equating coeffcient, we get
A + C = 0
B = 1 and C = 1
∴ A = – c
A = – 1

Question 8.
Find the general solution of the following differential equation:
x\(\frac{d y}{d x}\) = yx sin\(\left(\frac{y}{x}\right)\)
OR
Find the particular solution of the following differential equation, given that
y = 0 when x = \(\frac{\pi}{4}\)
\(\frac{d y}{d x}\) + y cot x = \(\frac{2}{1+\sin x}\)
Answer:
We have the differential equation:
x\(\frac{d y}{d x}\) = y – x sin\(\left(\frac{y}{x}\right)\)
The equation is a homogeneous differential equation.
Putting y = vx
⇒ \(\frac{d y}{d x}\) = v + x\(\frac{d v}{d x}\)
The differential equation becomes
v + x\(\frac{d y}{d x}\) = v – sin v
⇒ \(\frac{d v}{\sin v}\) = –\(\frac{d x}{x}\)
⇒ cosec vdx = –\(\frac{d x}{x}\)
Integrating both sides, we get
log|cosec v – cot v| = – log |x| + log K, K > 0 (Here, log K is an arbitrary constant)
⇒ log |(cosec v – cot v) x| = log K
⇒ | (cosec v – cot v) x| = K
⇒ (cosec v – cot v) x = ±K
⇒ \(\left({cosec} \frac{y}{x}-\cot \frac{y}{x}\right)\)x = C, which is the required general solution.
OR
OR
The differential equation is a linear differential equation.
IF = e^{∫cot xdx} = e^{l0g sinx} = sin x
The general solution is given by

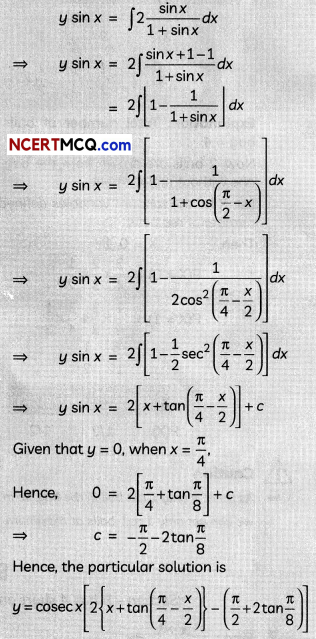
Explanation:
given, differential equation is:
x\(\frac{d y}{d x}\) = y – x sin\(\left(\frac{y}{x}\right)\)
The given equation is a homogeneous differential equation.

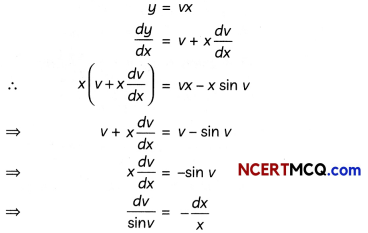
⇒ cosec v dv = \(\frac{d y}{d x}\)
on integrating both sides
∫cosec v dv = ∫ –\(\frac{d x}{x}\)
⇒ log |cosec v – cot v| = – log x + log C
⇒ log (cosec v – cot v) + log x = log C
⇒ x(cosec v – cot v) = C
is the required general solution.
OR
given, differential equation
\(\frac{d y}{d x}\) + y cot x = \(\frac{2}{1+\sin x}\)
The given differential equation is of the form
\(\frac{d y}{d x}\) + P(x) = Q(x)
Here, P(x) = cot x, Q(x) = \(\frac{2}{1+\sin x}\)
Then, I.F. = e^∫p(x)dx = e^{∫cot x.dx}
= e^{log sin x} = sin x
Then, general solution is given by:

Concept Applied:
The function f(x, y) in a homogeneous differential equation is a homogeneous function such that f(λx, λy) = λⁿ f(x, y) for any non-zero constant λ.

Question 9.

Answer:

Explanation:
Given

Question 10.
Find the shortest distance between the following lines:
\(\vec{r}\) = (î + ĵ – k̂) + s(2î + ĵ – k̂)
\(\vec{r}\) = (î + ĵ + 2k̂) + t(4î + 2ĵ – 2k̂)
OR
Find the vector and the cartesian equations of the plane containing the point î + 2ĵ – k̂ and parallel to the lines \(\vec{r}\) = (î + 2ĵ + 2k̂) + s(2î – 3ĵ + 2k̂) = 0 and \(\vec{r}\) = (3î + ĵ – 2k̂) + t((î – 3ĵ + k̂)) = 0
Answer:
Here, the lines are parallel The shortest distance
= \(\frac{\left|\left(\vec{a}_{2}-\vec{a}_{1}\right) \times \vec{b}\right|}{|\vec{b}|}\) = \(\frac{|(3 \hat{k}) \times(2 \hat{i}+\hat{j}+\hat{k})|}{\sqrt{4+1+1}}\)
(3k̂) × (2î + ĵ + k̂) = \(\left|\begin{array}{lll}
\hat{i} & \hat{j} & \hat{k} \\
0 & 0 & 3 \\
2 & 1 & 1
\end{array}\right|\) = – 3î + 6ĵ
Hence, the required shortest distance = \(\frac{3 \sqrt{5}}{\sqrt{6}}\) units
OR
Since, the plane is parallel to the given lines, the cross product of the vectors 2î – 3ĵ + 2k̂ and î – 3 ĵ + k̂ will be a normal to the plane (2î – 3ĵ + 2k̂) × (î – 3 ĵ + k̂) = 3î – 3k̂
The vector equation of the plane is
\(\vec{r}\) . (3î – 3k̂) = (î + 2ĵ – k̂) . (3î – 3k̂) or \(\vec{r}\) . (î – k̂) = 2
and the cartesian equation of the plane is x – z -2 = 0.

Explanation: The given, equation of lines are

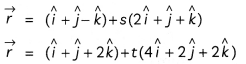
The shortest distance, between the likes are given by: = \(\frac{\left|\left(\vec{a}_{2}-\vec{a}_{1}\right) \times \vec{b}\right|}{|\vec{b}|}\)
Here,
\(\vec{a}_{1}\) = (î + ĵ – k̂)
\(\vec{a}_{2}\) = (î + ĵ – k̂)
\(\vec{b}\) = 2î + ĵ + k̂
∴ Distance between parallel lines

Caution:
Here, both the lines given are parallel so use the formula accordingly to get the answer.
OR
The given equation of the lines are

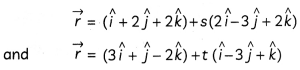
Now, the plane is parallel to the both equal of the lines.
Therefore, plane will be normal to the cross product of vectors 2î – 3ĵ + 2k̂ and î – 3ĵ + k̂.
= \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & -3 & 2 \\
1 & -3 & 1
\end{array}\right|\)
= î(- 3 + 6) – ĵ(2 – 2) + k̂(- 6 + 3)
= 3î – 0ĵ – 3k̂
= 3î – 3k̂
And the equation of the plane contains the point (î + 2ĵ – k̂)

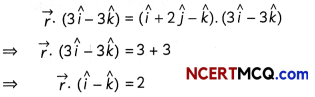
and the cartesian form of the equation of the plane will be x – z = 2 or x – z – 2 = 0.

Section – C
(Section – C has 4 Long answer type questions (LA) of 4 marks each.)

Question 11.
Evaluate:

Answer:
The given definite integral

Explanation: Consider,

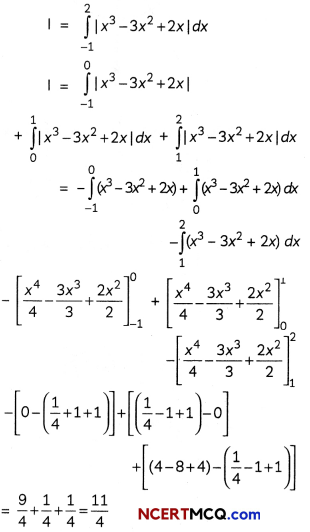
Question 12.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y² = x and the x-axis.
OR
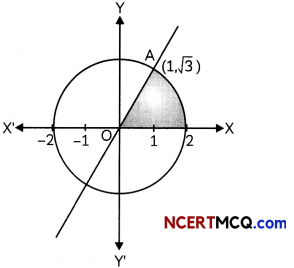
Using integration, find the area of the region :{(x, y):0 ≤ y ≤ √3x, x² + y² ≤ 4}
Answer:
Solving x + y = 2 and y² = x simultaneously, we get the points of intersection as (1, 1) and (4, – 2).

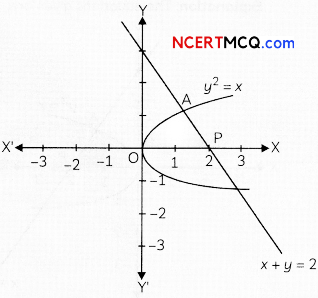
The required area = the shaded area =

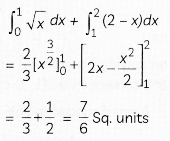
OR
Solving y = √3x and x² + y² = 4, we get the points of intersection as (1, √3) and (- 1, – √3).

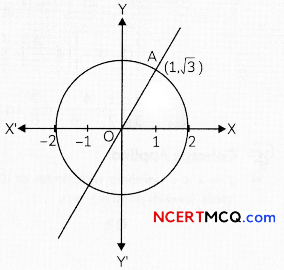
The required area = the shaded area

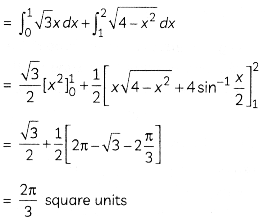
Explanation: The equations given are:

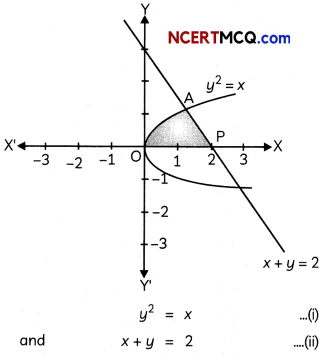
on solving equation (i) and (ii), we get points of intersection as (1, 1) and (4, -2).
∴ Area of shaded region

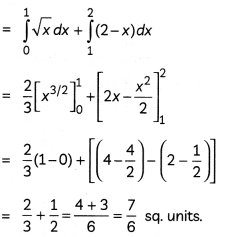
Concept Applied:
y² = x is a parabola with vertex at (0, 0) and it opens towards positive x-axis.
OR
Here, the given equation are
y = √3 ….. (i)
and x² + y² = 4 …(ii)
on solving (i) and (ii), we get
x² + (√3x)² = 4
⇒ x² + 3x² = 4
⇒ 4x² = 4 ⇒ x² = 1
Then, x = ±1
when x = 1, y = √3
when x = – 1, y = -√3
Then, points of intersection are (1, √3) and (-1 -√3)
Then,

Question 13.
Find the foot of the perpendicular from the point (1, 2, 0) upon the plane x – 3y + 2z = 9. Hence, find the distance of the point (1, 2, 0) from the given plane.
Answer:
The equation of the line perpendicular to the plane and passing through the point (1, 2, 0) is
\(\frac{x-1}{1}=\frac{y-2}{-3}=\frac{z}{2}\)
The coordinates of the foot of the perpendicular are (µ + 1, – 3µ + 2, 2µ) for some µ.
These coordinates will satisfy the equation of the plane. Hence, we have
µ + 1 – 3(- 3µ + 2) + 2(2µ) = 9
⇒ µ = 1
The foot of the perpendicular is (2, – 1, 2).
Hence, the required distance
= \(\sqrt{(1-2)^{2}+(2+1)^{2}+(0-2)^{2}}\)
= √l4 units

Explanation: The equation of the plane is x – 3y + 2z = 9.
From the point (1, 2, 0) a perpendicular is dropped on the plane x – 3y + 2z = 9.
So, the equation of the line perpendicular to the given plane and passing through the point (1, 2, 0) is:
\(\frac{x-1}{1}\) = \(\frac{y-2}{- 3}\) = \(\frac{z}{2}\) = λ
Then, consider the coordinates of the foot of the perpendicular as (λ + 1, – 3λ + 2, 2λ)
Since, these points lies on the equation of the place, therefore, it will satisfy it
∴ (λ + 1) – 3(- 3λ + 2) + 2 (2λ) = 9
⇒ 14λ = 14 ⇒ λ = 1
Therefore, the required point or foot of the perpendicular is: (1 + 1, – 3 × 1 + 1, 2 × 1) i.e. (2, -1, 2)
Required perpendicular distance
= \(\sqrt{(1-2)^{2}+(2+1)^{2}+(0-2)^{2}}\)
= \(\sqrt{1+9+4}\)
= √l4 units

CASE-BASED/DATA-BASED

Question 14.

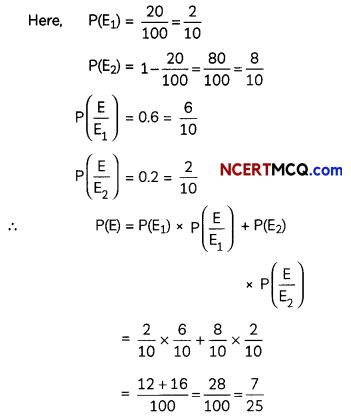
An insurance company believes that people can be divided into two classes: those who are accident prone and those who are not. The company’s statistics show that an accident-prone person will have an accident at sometime within a fixed one-year period with probability 0.6, whereas this probability is 0.2 for a person who is not accident prone. The company knows that 20 percent of the population is accident prone.

Based on the given information, answer the following questions.
(i) What is the probability that a new policyholder will have an accident within a year of purchasing a policy?
(ii) Suppose that a new policyholder has an accident within a year of purchasing a policy. What is the probability that he or she is accident prone?
Answer:
Let E₁ = The policyholder is accident prone.
E₂= The policyholder is not accident prone.
E = The new policy holder has an accident within a year of purchasing a policy.

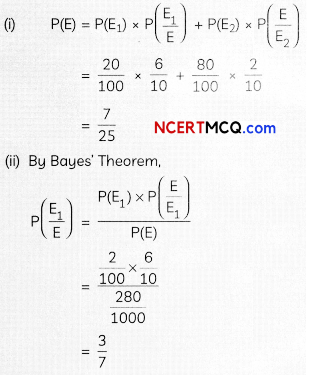
Explanation: Consider E₁ = Policy holder is prove to
E₂ = Policy holder is not prove to accident
E₃ = Policy holder met with an accident in year of purchase.
(i)

(ii) Here, we need to find the probability of P\(\left(\frac{\mathrm{E}_{1}}{\mathrm{E}}\right)\)
So, by Baye’s theorem

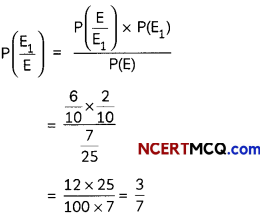
Caution:Read the case carefully, to get an idea about the probabilites given and what is needed to be calculated to get the desired results.