CBSE Sample Papers for Class 12 Maths Term 2 Set 11 for Practice

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 11 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 11 for Practice

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.

Question 2.
Solve the differential equation
\(\frac{d y}{d x}\) + 2x = e^3x
OR
Find the particular solution of the differential equation cot\(\left(\frac{d y}{d x}\right)\) = a (- 1 ≤ a ≤ 1), given that

Question 3.
If \(\vec{b} \times \vec{c}=\vec{c} \times \vec{a} \neq \overrightarrow{0}\), then show that \(\vec{a}+\vec{b}=k \vec{c}\) = kc, where k is a scalar. (2)

Question 4.
Show that \(|\vec{a}| \vec{b}+|\vec{b}| \vec{a}\) is perpendicular \(|\vec{a}| \vec{b}-|\vec{b}| \vec{a}\), for any two non-zero vectors \(\vec{a}\) and \(\vec{b}\) (2)

Question 5.
Let X represents the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are the possible values of X? (2)

Question 6.
Find the probability of the occurrence of a number greater than 2 in a throw of a die1 if it is know that only even numbers can occur. (2)

SECTION – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Find the sine of the angle between the vectors
\(\vec{a}\) = 3î + ĵ + 2k̂ and \(\vec{b}\) = 2î – 2ĵ + 4k̂
OR
Using vectors, show that the angle in a semi-circle is a right angle. (3)

Question 8.
Evaluate \(\int \frac{2 x+1}{\sqrt{x^{2}+4 x+3}}\)dx. (3)

Question 9.
The lines \(\frac{x-2}{1}=\frac{y-3}{1}=\frac{z-4}{-k}\) and \(\frac{x-1}{k}=\frac{y-4}{2}=\frac{z-5}{1}\) are coplanar. Find k.
OR
Find the cartesian equation of a plane that passes through the point (3, – 6, 4) and normal to the line joining the points (2, – 1, 5) and (3, 4, – 1). (3)

Question 10.
Find the particular solution of the differential equation (1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\), given that y = 0 when x = 1. (3)

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
Prove that the lines x = ay + b = cz + d and x = αy + β = γz + δ are coplanar, if (γ – c) (αβ – bα) – (α – a) (cδ – dγ) = 0. (4)

Question 12.
Let X denotes the number of colleges where you will apply after your result and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that

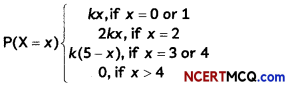
where k is a positive constant. Find the value of k. Also, find the probability that you will get admission in (A) exactly one college, (B) at most 2 colleges, (C) at least 2 colleges.
OR
Three persons A, B, C throw a die in succession till one gets a six and wins the game. Find their respective probabilities of winning, if A begins the game. (4)

Question 13.
Evaluate

CASE-BASED/DATA-BASED

Question 14.
Three friends, Anmol, Sanjay, and Sammer live in a same society. Location of their houses in the society is represented by the points A(-l, 0), B(l, 3) and C(3, 2) as shown in the figure.

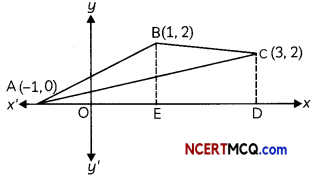
Based on the above information, answer the following two questions:
(A) Find the equation of the lines AB, BC and CA. (2)
(B) Find the area of the region of ABCDA. (2)