Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 12 Maths Term 2 Set 2 with Solutions
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- This question paper contains three sections-A. B and C. Each part is compulsory.
- Section-A has 6 short answer type (SA1) questions of 2 marks each.
- Section-B has 4 short answer type (SA2) questions of 3 marks each.
- Section-C has 4 long answer type questions (LA) of 4 marks each.
- There is an Internal choice in some of the questions.
- Q14 is a case-based problem having 2 sub parts of 2 marks each.
Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)
Question 1.
Let E and F be two events such that P(E) = \(\frac{1}{3}\), P(F) = \(\frac{1}{4}\), and P(E uF) = \(\frac{1}{2}\).Show that E and F are independent events. (2)
Answer:
We know,
P(E ∪ F) = P(E) + P(F) – P(E ∩ F)
⇒ P(E ∩ F) = P(E) + P(F) – P(E ∪ F)
= \(\frac{1}{3}+\frac{1}{4}-\frac{1}{2}=\frac{1}{12}\)
Also, P(E) × P(F) = \(\frac{1}{3} \times \frac{1}{4}=\frac{1}{12}\)
∵ P(E) × P(F) = P(E ∩ F)
∴ E and F are independent events.
Question 2.
Find the cosine of the angle between the vectors \(\vec{a}\) and \(\vec{b}\), where \(\vec{a}\) = 3î – 2ĵ – k̂ and \(\vec{b}\) = -2ĵ.
OR
Find λ and µ (2î + 6ĵ + 27k̂) × (î + j + pk̂) = 0 (2)
Answer:
Let the angle between the vector \(\vec{a}\) and \(\vec{b}\) be θ.
Then, cos θ = \(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\)
⇒ cos θ = \(\frac{(3 \hat{i}-2 \hat{j}-\hat{k}) \cdot(-2 \hat{j})}{|3 \hat{i}-2 \hat{j}-\hat{k} \|-2 \hat{j}|}\) ………(i)
Here, (3î – 2ĵ – k̂).(-2ĵ) = -6î.ĵ + 4ĵ.ĵ + 2k̂.ĵ
= 0 + 4 + 0
= 4
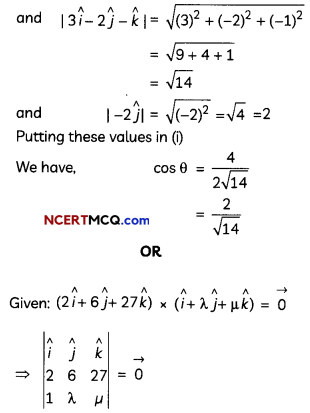
⇒ (6µ – 27λ)î – (2µ – 27)ĵ +(2λ – 6)k̂ = 0
⇒ 6µ – 27λ = 0
⇒ 2µ – 27 = 0
⇒ 2λ – 6 = 0
⇒ λ = 3
µ = \(\frac{27}{2}\)
![]()
Question 3.
Evaluate ∫ log x dx. (2)
Answer:
Let I = ∫ log x dx
![]()
Using integrating formu[a for a product of two functions.
= logx.∫1 dx – ∫[\(\frac{d}{d x}\)(log x).∫1.dx]dx
= x log x – ∫\(\frac{1}{x}\) . x dx
= x log x – ∫1dx
= x tog x – x + C
Question 4.
if the foot of a perpendicular drawn from origin to a plane is (5, – 3, – 2), then find the equation of the plane. (2)
Answer:
We know, general equation of a plane is a(x – x1) + b(y – y1) + c(z – z1) = 0 0(0,0,0)
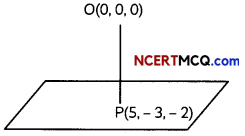
From the figure, normal to the required plane is OP.
where, \(\vec{OP}\) = (5 – 0)î + (- 3 – 0) ĵ + (- 2 – 0)k̂
= 5î – 3ĵ – 2k̂
(a, b, c) = (5, -3, -2)
Also, the plane contains the point P(5, – 3, -2)
∴ Required equation of plane is:
5(x – 5) + (- 3) (y + 3) + (- 2) (z + 2) = 0
⇒ 5x – 3y – 2z – 38 = 0
Question 5.
Evaluate (2)
![]()
Answer:
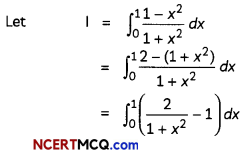
= [2 tan-1x – x]10
= [(2 tan-11 – 1) — (2 tan-1 0 – 0)]
= [(2.\(\frac{\pi}{4}\) – 1) – o]
= \(\frac{\pi}{2}\) – 1
Question 6.
Two cards are drawn successively without replacement from a well-shuffled pack of 52 playing cards. Find the probability distribution of the number of kings. (2)
Answer:
Let x denote the discrete random variable ‘the number of king1.
Then, x takes values 0, 1, and 2.
∴ P(X = 0) = P(both cards are not king)
= \(\frac{{ }^{48} C_{2}}{{ }^{52} C_{2}}=\frac{48 \times 47}{52 \times 51}=\frac{188}{221}\)
P(X = 1) = P(one card is king)
= \(\frac{{ }^{48} C_{1} \times{ }^{4} C_{1}}{{ }^{52} C_{2}}=\frac{48 \times 4 \times 2}{52 \times 51}=\frac{32}{221}\)
P(X = 2) = P(both ore king cards)
= \(\frac{{ }^{4} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}=\frac{4 \times 3}{52 \times 51}=\frac{1}{221}\)
So, the required probabiLity distribution of X is

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)
Question 7.
Solve the differential equation
(1 + y2) tan-1 x dx + 2y (1 + x2)dy = 0. (3)
Answer:
Given, differentiaL equation is
(1 + y2)tan-1xdx + 2y(1 + x2)dy = 0
⇒ (1 + y2)tan-1xdx = -2y(1 + x2)dy
⇒ \(\left(\frac{\tan ^{-1} x}{1+x^{2}}\right)\)dx = \(\left(\frac{-2 y}{1+y^{2}}\right)\)dy
On integrating both sides, we get
∫\(\frac{\tan ^{-1} x}{1+x^{2}}\)dx = ∫\(\frac{2 y}{1+y^{2}}\)dy
Put tan-1 x = t in LHS. we get
\(\frac{1}{1+x^{2}}\)dx = dt
Put 1 + y2 = u in RHS, we get
2y dy = du
∫t dt = ∫\(\frac{d u}{u}\)
⇒ \(\frac{t^{2}}{2}\) = – log u + c
⇒ (tan-1x)2= – log(1 + y2)+c
⇒ (tan-1 x)2 + log(1 + y2)=c
which is the required soLution of the given differential equation.
![]()
Question 8.
Three vectors \(\vec{a}, \vec{b}\) and \(\vec{c}, \vec{a}\) satisfy the condition \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\) . Evaluate the quantity µ = \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\), if |\(\vec{a}\)|= 3, |\(\vec{b}\)|= 4 and |\(\vec{c}\)| = 2.
OR
Let \(\vec{a}\) = 2î + k̂, \(\vec{b}\) = î + ĵ + k̂ and \(\vec{c}\) = 4î – 3ĵ + 7 k̂. Find a vector \(\vec{r}\) which satisfies \(\vec{r} \times \vec{b}=\vec{c} \times \vec{b}\) and \(\vec{r} \cdot \vec{a}\) = 0. (3)
Answer:
Given
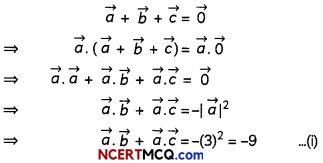
Similarly, \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}=-|\vec{b}|^{2}\) = -16 …(ii)
And, \(\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}=-|\vec{c}|^{2}\) =—4 ………..(iii)
Adding (i), (ii) and (iii), we have
2(\((\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a})\)) = 9 – 16 – 4
= – 29
Since μ = \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\) (Given)
2 × μ = -29
= \(\frac{-29}{2}\)
Hence, the value of μ is \(\frac{-29}{2}\).
OR
Let the vector \(\vec{r}\) be given as xî + yĵ + zk̂
Now, \(\vec{r} \cdot \vec{a}\) = 0
⇒ (xî + yĵ + zk̂).(2î + k̂) = 0
⇒ 2x + z = 0 …(i)
Also, \(\vec{r} \times \vec{b}=\vec{c} \times \vec{b}\)
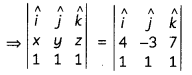
⇒ (y – z)î +(x – z)ĵ +(x – y)k̂ = – 10î – 3ĵ +7k̂
⇒ y – z = -10, x – z = -3. x – y = 7 ……….(ii)
Solving eq. (i) and (ii), we get
x = -1, y = -8, z = 2
∴ \(\vec{r}\) = -î – 8ĵ + 2k̂
Question 9.
Let a, b and c be three vectors such that \(\vec{a}\) ≠ 0 and \(\vec{a} \times \vec{b}=2 \vec{a} \times \vec{c}\), |\(\vec{a}\)| = |\(\vec{c}\)| = 1, |\(\vec{b}\)| = 4 and |\(\vec{b} \times \vec{c}\)| = \(\sqrt{15}\) , \(|\vec{b} \times \vec{c}|\) = λ\(\vec{a}\).Then find the value of λ. (3)
Answer:
Let angle between \(\vec{b}\) and \(\vec{c}\) be θ.
∵ \(|\vec{b} \times \vec{c}|\)
\(|\vec{b}| \cdot|\vec{c}|\) sin θ = \(\sqrt{15}\)
⇒ (4) (1) sin θ = \(\sqrt{15}\)
⇒ sin θ = \(\frac{\sqrt{15}}{4}\)
⇒ cos θ = \(\frac{1}{4}\)
Now, \(\vec{b}\) – 2\(\vec{c}\) = λ\(\vec{a}\)
Taking mode both sides, we get
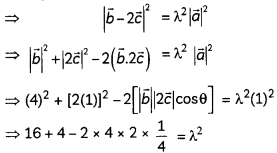
⇒ 16 = λ2
⇒ λ = 4
Hence, the value of λ is 4.
Question 10.
Evaluate ∫\(\frac{1}{x^{1 / 2}+x^{1 / 4}}\)dx
OR
Evaluate ∫2-1f(x) dx, where f(x) = |x + 1| + |x| + |x – 1|. (3)
Answer:
Let I = ∫\(\frac{1}{x^{1 / 2}+x^{1 / 4}}\)dx
Put x = t4
⇒ dx = 4t3
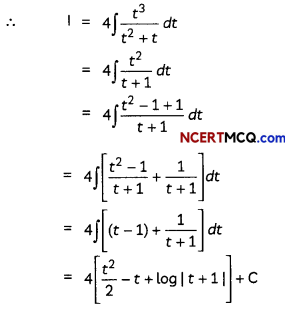
We have,
f(x) = |x + 1| + |x| + |x – 1|
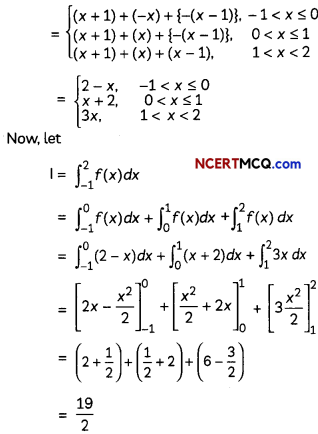
Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)
Question 11.
Find the area of the region bounded by the curve y = cos x between x = 0 and x = π.
OR
Find the area of the region bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7. (4)
Answer:
The graph of cosine function is positive from 0 to \(\frac{\pi}{2}\) and negative from \(\frac{\pi}{2}\) to π.

= (1 + 0) + (0 + 1)
= 1 + 1 = 2 sq. units
OR
Given equations of the lines are x + 2y = 2, y – x = 1 and 2x + y = 7.
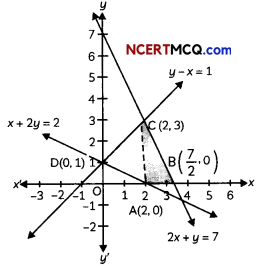
These lines intersect each other at points C(2, 3), D(0, 1) and E(4, – 1).
∴ Required area = ar(OACDO) + ar(ABCA) – ar(OADO) + ar(AEFBA) – ar(BEFB)

![]()
Question 12.
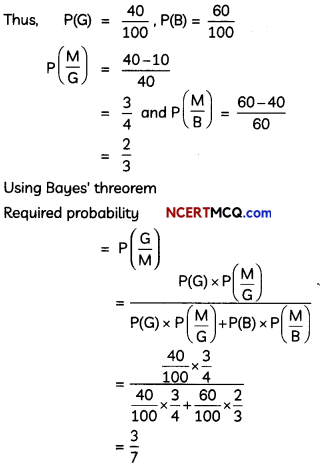
It is known that 40% of the students in a certain college are girls and 50% of the students are above the median height. If \(\frac{2}{3}\) of boys are above the median height, what is the probability that a randomly selected student who is below the median height is a girl? (4)
Answer:
Let the total number of students in the college be 100. Then, 40 are girls and 60 are boys.
Here, \(\frac{2}{3}\), of boys are above the median height
i.e., \(\frac{2}{3}\) × 60 = 40 boys are above the median height
Since, only 50 students are above the median height, so only 10 girls are above the median height.
Now, let the event G, B and M are described as:
G : A girl is selected.
B : A boy is.
M : Student selected is below the median height
Question 13.
Evaluate ∫01 tan-1\(\left(\frac{2 x}{1-x^{2}}\right)\)dx (4)
Answer:
Let I = ∫01 tan-1\(\left(\frac{2 x}{1-x^{2}}\right)\)dx
Put x = tan y
⇒ dx = sec2y dy
For x = 0, y = tan-1 0 = 0
For x = 1, y = tan-1 1 = \(\frac{\pi}{4}\)

![]()
Case-Based/Data-Based
Question 14.
A football match is organized between students of class XII of two schools, say school A and school B. For each, a team from each school is chosen. Remaining students of Class XII of schools A and B are respectively sitting on the plane represented by the equations \(\vec{r}\)(î + ĵ + 2k̂) = 5 and \(\vec{r}\)(2î – ĵ + k̂) = 6, to cheer up the team of their respective school.

Based on the above information, answer the following two questions:
(i) Write the cartesian equation of the plane on which students of school A are seated. (2)
Answer:
Vector equation of plane on which students of school A are seated is:
\(\vec{r}\) .(î + ĵ + 2k̂) = 5
⇒ (xî + yĵ + zk̂).(î + ĵ + 2k̂) =5
⇒ x + y + 2z = 5
which is the required cartesian form.
(ii) Write the intercept form of the equation of the plane on which students of school B are seated. Also, find the distance of this plane from the origin. (2)
Answer:
Cartesian equation of the plane on which students of school B are seated is x – y + z = 6.
\(\frac{2 x}{6}-\frac{y}{6}+\frac{z}{6}\) = 1
\(\frac{x}{3}+\frac{y}{-6}+\frac{z}{6}\) = 1
Which is the required intercept form.
Its distance from the origin = \(\left|\frac{-6}{\sqrt{4+1+1}}\right|\)
= √6 units