CBSE Sample Papers for Class 12 Maths Term 2 Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 3 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Evaluate ∫\(\frac{2^{x+1}-5^{x-1}}{10^{x}}\) dx. (2)
Answer:
Let I = ∫\(\frac{2^{x+1}-5^{x-1}}{10^{x}}\) dx

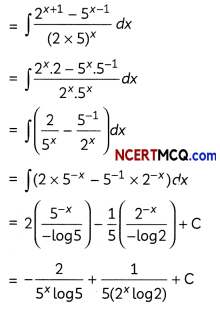
Question 2.
A line makes angle α, β, γ with the coordinate axes. If α + β = 90°, then find the value of γ. (2)
Answer:
If a tine makes angles α, β, γ with coordinate axes, then we have,
cos² α + cos²β + cos²γ = 1
Since, α + β = 90°
⇒ α = 90° – β
⇒ cos α = cos (90° – β)
⇒ cos α = sin β
⇒ cos²α = sin²β
= 1 – cos²β
⇒ cos²α + cos²β = 1
From (i) and (ii), we get
⇒ 1 + cos²γ = 1
⇒ cos²γ = 0
Hence, γ = \(\frac{\pi}{2}\) = 90°

Question 3.
Find the probability of the occurrence of a number greater than 2 in a throw of a die, if it is known that only even numbers can occur.
OR
An unbaised die is thrown. If a random variable X is defined as

Write the probability distribution of X. (2)
Answer:
Let A be the event of “occurrence of an even number”, and B be the event of “occurrence of a number greater than 2.
∴ P(A) = \(\frac{3}{6}=\frac{1}{2}\)
And P(B n A) = \(\frac{2}{6}=\frac{1}{3}\)
[∵ 4 and 6 are even numbers from 1 to 6 that are greater than 2]
Now,
Required probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{1 / 3}{1 / 2}=\frac{2}{3}\)
OR
Here, X takes the values 0 and 1.
Also, P(X = 0) = P(an odd number = \(\frac{3}{6}=\frac{1}{2}\)
And, P(X = 1) = P(an even number) = \(\frac{3}{6}=\frac{1}{2}\)
Thus, the probability distribution of X is:

Question 4.
If \(\vec{a}\) = 5î – ĵ – 3k̂ and \(\vec{b}\) = î + 3ĵ – 5k̂, then show that \((\vec{a}+\vec{b})\) and \((\vec{a}-\vec{b})\) are orthogonal. (2)
Answer:
We have,
\(\vec{a}+\vec{b}\) = (5î – ĵ – 3k̂) + (î + 3ĵ – 5k̂)
= 6î + 2ĵ – 8k̂
and \(\vec{a}-\vec{b}\) = (5î – ĵ – 3k̂) – (î + 3ĵ – 5k̂)
= 4î – 4ĵ + 2k̂

Now, \((\vec{a}+\vec{b})\). \((\vec{a}-\vec{b})\) = (6î + 2ĵ – 8k̂) . (4î – 4ĵ + 2k̂)
= 6 × 4 + 2 × (- 4) + (- 8) × 2
= 24 – 8 – 16
= 0

Hence, \((\vec{a}+\vec{b})\) and \((\vec{a}-\vec{b})\) are orthogonal i.e., perpendicular to each other.

Question 5.
Check whether the differential equation (x – y) \(\frac{d y}{d x}\) = x + 2y is homogenous or not. (2)
Answer:
We have,

Since, the power of λ is zero.
∴ The given differential equation is homogeneous.

Question 6.
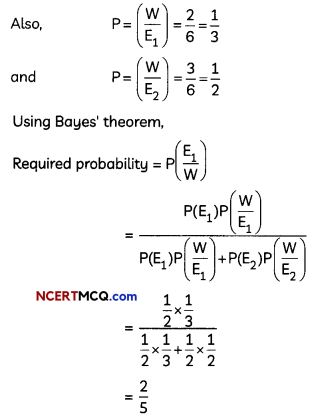
Bag I contains 2 white and 4 red balls. Bag II contains 3 white and 3 red balls. One of the bags is selected at random and a ball is drawn from it. If the ball drawn is white, what is the probability that it is drawn from Bag I? (2)
Answer:
Let E₁ and E₂ be the events of selecting Bag I and Bag II respectively.
Also, let W be the event of drawing a white ball. Then,
P(E₁)= \(\frac{1}{2}\) and P(E₂) = \(\frac{1}{2}\)

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Evaluate ∫tan^-1(secx + tanx)dx.
OR
Evaluate ∫₀¹ \(\frac{1}{\sqrt{a x-x^{2}}}\) dx. (3)
Answer:
Let ∫tan^-1(secx + tanx)dx.

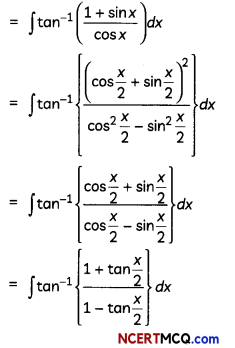
[Dividing numerator and denominator by \(\frac{x}{2}\)]

Question 8.
Find the general solution of y² dx + (x² – xy + y²) dy = 0. (3)
Answer:
Given, diffrentiaL equation is
y²dx + (x² – xy + y²)dy =0
⇒ y²dx = -(x² – xy + y²)dy
⇒ y² \(\frac{d x}{d y}\) = -(x² – xy + y²)
⇒ \(\frac{d x}{d y}=-\left(\frac{x^{2}}{y^{2}}-\frac{x}{y}+1\right)\) ……(i)
This is a homogeneous differential equation.

Let x = vy …….(ii)
\(\frac{d x}{d y}\) = v + y\(\frac{d v}{d y}\)
Substituting these values in equation (i), we get
v + y\(\frac{d v}{d y}\) = -(v² – v + 1)
⇒ y\(\frac{d v}{d y}\) = -v² – 1
⇒ \(\frac{d v}{d y}\)

On integrating both sides, we get
tan^-1(y) = -log y + c
⇒ tan^-1\(\) + log y = c [From (ii)]

Caution:
Here, we are differentiating x w.r.t y so we will use x = vy for substitution.

Question 9.
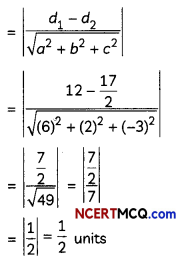
Find the distance between the parallel planes 6x + 2y – 3z = 12 and 12x + 4y – 6z = 17. (3)
Answer:
Given: Equation of ptanes ore:
6x + 2y – 3z = 12 ………(i)
and 12x + 4y – 6z = 17
or 6x + 2y – 3z = \(\frac{17}{2}\)
∵ Planes (1) and (ii) are paralleL

∴ Distance between them

Related Theory:
Distance between two parallel planes ax + by + cz = d₁ and ax + by + cz = d₂ is given as \(\left|\frac{d_{1}-d_{2}}{\sqrt{a^{2}+b^{2}+c^{2}}}\right|\)

Question 10.
Let the vectors \(\vec{a}, \vec{b}, \vec{c}\) be given as a₁x î + a₂ĵ + a₃ k̂, b₁î + b₂ĵ + b₃k̂ and c₁î + c₂ĵ + c₃k̂ respectively. Then show that \(\vec{a} \times(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+(\vec{a} \times \vec{c})\)
OR
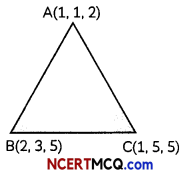
Find the area of the triangle whose vertices are A (1,1,2), B (2, 3, 5) and C (1, 5, 5). (3)
Answer:
We have,
\(\vec{b}+\vec{c}\) = (b₁î + b₂ĵ + b₃k̂) + (c₁î + c₂ĵ + c₃k̂)
= (b₁ + c₁)î + (bsub>2 + csub>2)ĵ + (b₃ + c₃) k̂

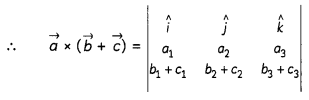
= {a₂ (b₃ + c₃) – a₃ (b₂ + c₂)}î – {a₁ (b₃ + c₃) – a₃(b₁ + c₁}ĵ + {a₁(b₂ + c₂) – a₂(b₁ + c₁)k̂

So \((\vec{a} \times \vec{b})+(\vec{a} \times \vec{c})\) = (a₂b₃ – a₃b₂)î – (a₁b₃ – a₃b₁)ĵ + (a₁b₂ – a₂b₁) k̂ + (a₁c₃ – a₃c₁) î -(a₁c₃ – a₃c₁)ĵ + (a₁c₂ – a₂c₁) k̂
= {a₂(b₃ + c₁) – a₃(b₂ + c₂)} î – {a₁(b₃ + c₃) – a₃(b₁ + c₁}ĵ + {i (b₂ + c₂) – 2 (b₁ + c₁)} k̂ …(iv)

From (i) and (iv), we get
\(\vec{a} \times(\vec{b}+\vec{c})=(\vec{a}+\vec{b})+(\vec{a} \times \vec{c})\)
Hence proved.

OR

We have, \(\overrightarrow{\mathrm{AB}}\) = (2 – 1)î + (3 – 1)ĵ + (5 – 2) k̂
= î + 2ĵ + 3k̂

and \(\overrightarrow{\mathrm{AC}}\) = (1 – 1)î + (5 – 1)ĵ +(5 – 2)k̂
= 4ĵ +3k̂

We know,
Area of ∆ABC = \(\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|\)

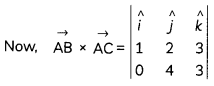
= (6 – 12)î – (3 – 0)ĵ + (4 – 0)k̂ – 6î – 3ĵ + 4k̂
∴\(|\overrightarrow{A B} \times \overrightarrow{A C}|=\sqrt{(-6)^{2}+(-3)^{2}+4^{2}}\)
= \(\sqrt{36+9+16}\)
= \(\sqrt{61}\)
∴ Area of ∆ABC = \(\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|=\frac{\sqrt{61}}{2}\)sq. units

Section – C
(Section – C has 4 Long answer type questions (LA) of 4 marks each.)

Question 11.
Evaluate ∫\(\frac{1}{3+2 \sin x+\cos x}\) dx
OR
Evaluate ∫₀^π/2\(\frac{\cos x}{1+\cos x+\sin x}\) dx. (4)
Answer:
Let I = ∫\(\frac{1}{3+2 \sin x+\cos x}\) dx

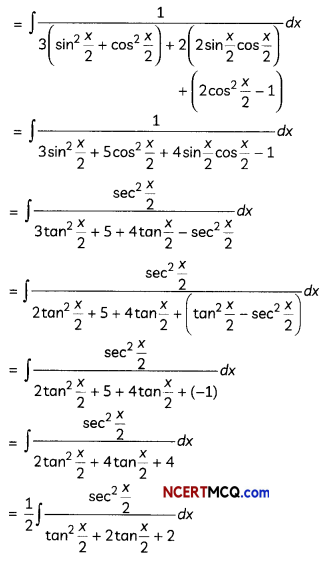
Put tan \(\frac{x}{2}\) = t
⇒ \(\frac{1}{2}\)sec²\(\frac{x}{2}\) dx = dt
⇒ sec²\(\frac{x}{2}\) dx = 2dt
∴ I = ∫\(\frac{d t}{t^{2}+2 t+2}\)
= ∫\(\frac{d t}{(t+1)^{2}+1}\)
= tan^-1(t + 1) + C
[∵∫\(\frac{1}{x^{2}+a^{2}}\)dx = \(\frac{1}{a}\)tan^-1\(\frac{x}{a}\)
= tan^-1(tan\(\frac{x}{2}\) + 1) + C
OR

Put 1 + tan\(\frac{x}{2}\) = t
⇒ \(\frac{1}{2}\)sec² \(\frac{x}{2}\)dx = dt
or sec² \(\frac{x}{2}\)dx = 2dt
Also, when x = 0, t = 1
when x = \(\frac{π}{2}\) t =2
∴ I₁ = ∫₁²\(\frac{d t}{t}\)
= [log t]₁²
= log 2

Substituting the value of I₁ in (iii), we get
2I = \(\frac{π}{2}\) – Log 2
⇒ I = \(\frac{π}{2}\) – \(\frac{1}{2}\)Log 2

Question 12.
Find the area bounded by the curve y = √x, x = 2y + 3 in the first quadrant and x-axis. (4)
Answer:
Given: y= √x and x = 2y + 3 in the first quadrant
Putting x = 2y + 3 in y = √x we get
y = \(\sqrt{2 y+3}\)
⇒ y² = 2y+3
⇒ y² – 2y – 3 = 0
⇒ y² – 3y + y – 3 = 0
⇒ y(y – 3) + 1(y – 3) = 0
⇒ (y + 1)(y – 3) = 0
⇒ y = -1, 3
∴ x = 1.9
∴ Points of intersection of the given curve and the line are (1, -1) and (9, 3).

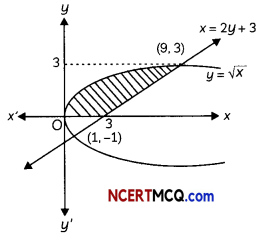
∴ Required area of shaded region

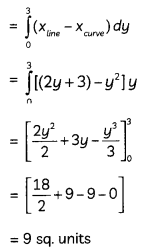
Question 13.
If î + ĵ + k̂, 2î +5ĵ, 3î + 2 ĵ – 3k̂ and î – 6ĵ – k̂ are the position vectors of points A, B, C and D respectively, then find the angle between the vectors \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{CD}}\). (4)
Answer:
We have, \(\overrightarrow{\mathrm{AB}}\) = (2 – 1)î + (5 – 1)ĵ + (0 – 1)k̂
= î + 4ĵ – k̂
And
\(\overrightarrow{\mathrm{CD}}\) = (1 – 3)î +(-6 – 2) + (-1 + 3)k̂
= -2î – 8ĵ + 2k̂

Let θ be the angle between the vectors \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{CD}}\)

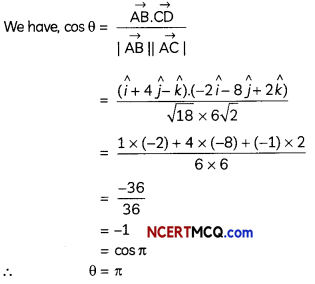
Hence the angle between the vectors \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{CD}}\) is π.

Case-Based/Data-Based

Question 14.
In an examination, an examinee either guesses or copies or knows the answer of MCQs with four choices. The probability that he makes a guess is \(\frac{1}{3}\), and the probability that he copies answer is \(\frac{1}{6}\). The probability that his answer is correct given that he copied it, is \(\frac{1}{8}\)

Based on the above information, answer the following two questions:
(A) What is the probability that he answers the question correctly? (2)
Answer:
Let E₁, E₂, E_3, and E be the events defined as follows:
E₁: Examinee guesses the answer.
E₂: Examinee copies the answer.
E₃: Examinee knows the answer.
E: Examinee answers the question correctly.
∴ P(E₁) = \(\frac{1}{3}\)
P(E₂) = \(\frac{1}{6}\)
P(E₃) = 1 – \(\left(\frac{1}{3}+\frac{1}{6}\right)=\frac{1}{2}\)

Also, = (Since, a question has four choices, out of which only one is correct.)
P\(\left(\frac{E}{E_{2}}\right)=\frac{1}{8}\)
P\(\left(\frac{E}{E_{3}}\right)\) = 1

(When the student knows the answer, the probability of his answer being correct is 100%.)

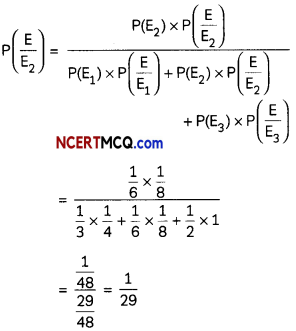
(A) P(E) = P(E₁) × P\(\left(\frac{E}{E_{1}}\right)\) + P\(\left(\frac{E}{E_{2}}\right)\) + P(E₃) × P\(\left(\frac{E}{E_{3}}\right)\)

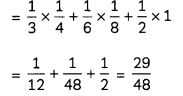
(B) Given that he answered the question correctly, what is the probability that he copied the answer? (2)
Answer: