CBSE Sample Papers for Class 12 Maths Term 2 Set 4 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 4 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 4 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
If A, B, C and D are the points with position vectors î + ĵ – k̂, 2î – ĵ + 3k̂, 2î – 3k̂, 3î – 2ĵ + k̂, respectively, find the projection of \(\overrightarrow{\mathrm{AB}}\) along \(\overrightarrow{C D}\). (2)
Answer:

Caution:
The formula for the projection of \(\vec{a}\) along \(\vec{b}\) is \(\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}\)

Question 2.
Find the area of the region bounded by the curve y² = 8x and the line x = 2. (2)
Answer:
y² = 8x represents a parabola whose vertex is at the origin, axis of symmetry is x-axis, focus on the positive direction of x-axis and it opens to the right.

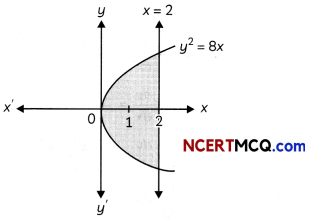
Since, the parabola is symmetrical about x-axis.

Question 3.
Evaluate ∫(2x + 5)sin2x dx.
OR
Evaluate

Answer:

Question 4.
8% of bulbs produced by a factory are red and 2% are red and defective. If one bulb is picked up at random, what is the probability of it being defective, if it is red? (2)
Answer:
Let A be the event of “the bulb being red”, and B be the event of “the bulb being defective”. Then,
∴ P(A) = \(\frac{8}{100}\) = 0.08
And, P(B ∩ A) = \(\frac{2}{100}\) = 0.02
Required probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{0.02}{0.08}\) = \(\frac{1}{4}\)

Question 5.
A bag contains 19 tickets, numbered from 1 to 19. A ticket is drawn and then another ticket is drawn without replacement. Find the probability that both tickets will show an even number. (2)
Answer:
Let A be the event that “first ticket shows an even number”.
∴ A = {2, 4, 6, 8,10,12,15,16,18}
∴ P(A) = \(\frac{9}{19}\)
Let B be the event that “second ticket shows an even number”.
Since, first ticket has not been replaced, so now there are 18 tickets, out of which 8 are even numbered.
∴ P(B/A) = \(\frac{8}{18}\)
Now, required probability
= P (both tickets are even numbered)
= P (A ∩ B)
= P (A) × P(B/A)
[Using multiplication theorem]
= \(\frac{9}{19} \times \frac{8}{18}=\frac{4}{19}\)

Question 6.
Show that the points A (2, – 1, 1), B (1, – 3, – 5) and C (3, – 4,- 4) are the vectors of a right angled triangle. (2)
Answer:

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Solve the differential equation:
x\(\frac{d y}{d x}\) + (2x + 1)y = xe^-2x
OR
Solve: xy \(\frac{d y}{d x}\) = x² – y²
Answer:
The given differential equation can be rewritten as dy 2x +1 _2x
\(\frac{d y}{d x}+\frac{2 x+1}{x} \cdot y\) = e^-2x
It is a linear differential equation in the form
\(\frac{d y}{d x}\) + P(x).y = Q(x)
where, P(x) = \(\frac{2 x+1}{x}\) and Q(x) = e^-2x
Integrating Factor (I.F.)
= e^∫P(x).dx = \(e^{\int\left(2+\frac{1}{x}\right) d x}\)
= e^{2x + log x}
= e^2x.e^{log x}
= e^2x.x
Thus, the solution to the given differential equation is:
y.(I.F.) = ∫Q(x).(I.F.)dx
⇒ y.(e^2x.x) = ∫e^-2x.(e^2x.x)dx
⇒ xye^2x = ∫ x dx
⇒ xye^2x = \(\frac{x^{2}}{2}\) + C
which is the required solution of the given differential equation.
OR
we have, xy\(\frac{d y}{d x}\) = x² – y²
or, \(\frac{d y}{d x}\) = \(\frac{x^{2}-y^{2}}{x y}\) …… (i)
Clearly, this differential equation is a homogeneous differential equation.
∴ Put y = vx
⇒ \(\frac{d y}{d x}\) = v + x\(\frac{d v}{d x}\)
Substituting these values in (i), we get

Question 8.
If with reference to the right handed system of mutually perpendicular unit vectors î, ĵ and k̂, \(\vec{\alpha}\) = 3î – ĵ and \( = 2î – ĵ – 3î, then express [latex]\vec{\beta}\) in the form \(\vec{\beta}=\overrightarrow{\beta_{1}}+\overrightarrow{\beta_{2}}\) , where \(\overrightarrow{\beta_{1}}\) is parallel to \(\vec{\alpha}\) and \(\overrightarrow{\beta_{2}}\) is perpendicular to \(\vec{\alpha}\). (3)
Answer:

Question 9.
Evaluate \(\int \frac{1}{x\left(x^{6}+1\right)}\) dx. (3)
Answer:

Question 10.
The lines \(\frac{x-2}{1}=\frac{y-3}{1}=\frac{z-4}{-k}\) and \(\frac{x-1}{k}\) = \(\frac{y-4}{2}=\frac{z-5}{1}\) are coplanar. Find k.
OR
Find the point(s) on the line \(\frac{x+2}{3}=\frac{y+1}{2}\) = \(\frac{z-3}{2}\), which are at a distance of 3√2 units from the point (1, 2, 3). (3)
Answer:
We know that the lines

⇒ -(1 + 2k) – 1(1 + k²) + 1 (2 – k) = 0
⇒ – 1 – 2k – 1 – k² + 2 – k = 0
⇒ k² + 3k = 0
⇒ k(k + 3) = 0
⇒ k = 0, – 3

Caution:
Lines will be coplanar, if they lie on the same plane.
OR
Given: Equation of line is
\(\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}\) = λ(say)
∴ Any point on the given line is
(3λ – 2, 2λ – 1, 2λ + 3) …….. (i)
Since, this point is at a distance of 3√2 units from the point (1, 2, 3).
∴ \(\sqrt{(3 \lambda-2-1)^{2}+(2 \lambda-1-2)^{2}+(2 \lambda+3-3)^{2}}\)
= 3√2 [Using distance formula]
or (3λ – 3)² + (2λ – 3)² + (2λ)² = 18 [Squaring both sides]
or 17λ² – 30λ. = 0
⇒ λ(17λ – 30) = 0
⇒ λ = 0, \(\frac{30}{17}\)
Substituting the values of λ in (i), we get the required points as (- 2, – 1, 3) and \(\left(\frac{56}{17}, \frac{43}{17}, \frac{111}{17}\right)\).

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
A letter is known to have come either from KOLKATA or TATANAGAR. On the envelope just two letters, TA, are visible. Find the probability that the letter has come from TATANAGAR.
OR
A doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, scooter or by other means of transport are respectively. \(\frac{3}{10}, \frac{1}{5}, \frac{1}{10}\) and the probabilities that he will be late are \(\frac{1}{4}, \frac{1}{3}\) and \(\frac{1}{12}\), if he comes by train, bus and scooter, respectively, but if he comes by other means of transport, then he will not be late, When he arrives, he is late. What is the probability that he came by train? (4)
Answer:
Let E₁, E₂ and F be the events defined as:
Ex: Letter has come from KOLKATA.
E2 : Letter has come from TATANAGAR.
and F: Two consecutive visible letters are TA.
∴ P(E₁) = P(E₂)= \(\frac{1}{2}\)
Now, the word KOLKATA has 7 Letters, so there are groups of two consecutive Letters, namely, KO, OL, LK, KA, AT and TA.
Only one of these is ‘TA’.
∴ \(P\left(\frac{F}{E_{1}}\right)=\frac{1}{6}\)
Similarly, the word TATANAGAR has a letters, and there are 8 groups of two consecutive letters, namely TA, AT, TA, AN, NA, AG, GA and AR.
Only here of these are ‘TA’.
∴ \(P\left(\frac{F}{E_{2}}\right)\) = \(\frac{2}{8}=\frac{1}{4}\)
Now,
required probability = p\(\left(\frac{E_{2}}{F}\right)\)

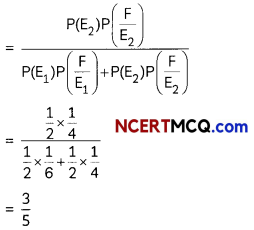
Let B be the event that the doctor visits the patient late.
Also, let A₁, A₂, A₃ and A₄ be the events that the doctor comes by train, bus, scooter and other means of transport, respectively.

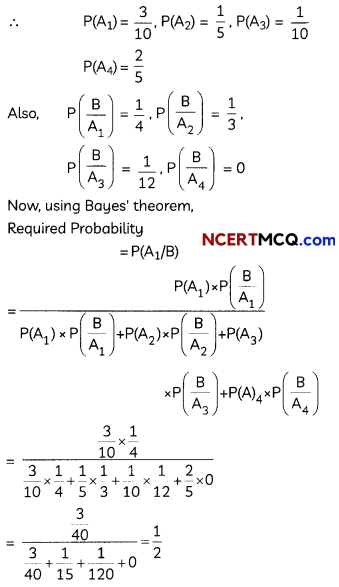
Question 12.
Evaluate

Answer:

Question 13.
Find the image of the point (1, 2, 3) in the plane x + 2y + 4z = 38. (4)
Answer:
Given: Equation of plane is:
x + 2y + 4z = 38 ……. (i)
∴ Unit vector normal to the plane is (î + 2 ĵ + 4k̂).
Now, equation of the line from point P(1, 2, 3), parallel to vector î + 2ĵ + 4k̂ will be
\(\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{4}\) = λ(say)
∴ Any general point on this line is (λ + 1, 2λ + 2, 4λ + 3).
Let N be the foot of perpendicular drawn from point P(1, 2, 3) to the plane (i).
Then, coordinates of N = (λ + 1, 2λ + 2, 4λ + 3)
Since, point N also lies on plane (i), so it must satisfy the equation of plane.
(λ + 1) + 2(2λ + 2) + 4 (4λ + 3) = 38
⇒ 21λ + 17 = 38
⇒ 21λ = 21
⇒ λ = 1
Putting the value of λ in the coordinates of N, we get
N = (1 + 1, 2(1) + 2, 4(1) + 3)
= (2, 4, 7)
Now, let P'(α, β, γ) be the image of point P(1, 2, 3) in the plane (i).
Then, N is mid-point of line joining the points P and P’.
∴ Using mid-point formula,
N(2, 4, 7) = \(\left(\frac{1+\alpha}{2}, \frac{2+\beta}{2}, \frac{3+\gamma}{2}\right)\)
⇒ (α, β, γ) = (3, 6, 11)
Thus, the required image of point (1, 2, 3) is (3, 6,11).

Case-Based/Data-Based

Question 14.
A mirror in the shape of an ellipse represented by \(\frac{x^{2}}{9}+\frac{y^{2}}{4}\) = 1 was hanging on the wall. Prem and his sister were playing with a ball in the room, even their mother stopped them to do so. All of a sudden, the ball hit the mirror and got a scratch in the shape of a line represented by \(\frac{x}{3}+\frac{y}{2}\) =1.

Based on the above information, answer the following two questions:
(A) Determine the points of intersection of the ellipse and the line. (2)
Answer:
We have

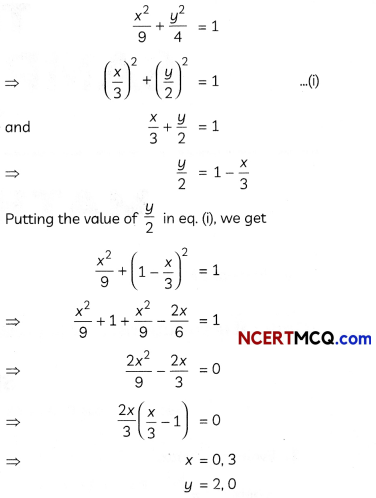
So, the required points of intersections are (0, 2) and (3, 0).

(B) Find the area of the smaller region bounded by the ellipse and the line. (2)
Answer: