CBSE Sample Papers for Class 12 Maths Term 2 Set 6 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 6 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 6 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Evaluate ∫sin^-1\(\left(\sqrt{\frac{1-\cos 2 x}{2}}\right)\)dx. (2)
Answer:
Let I = ∫sin^-1\(\left(\sqrt{\frac{1-\cos 2 x}{2}}\right)\)dx

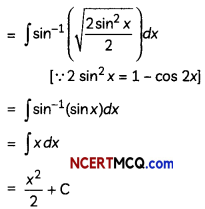
Question 2.
Check whether the differential equation (4x + 6y + 5)dx – (3x + 2y + 4) dy = 0 is homogeneous or not.
OR
Find the solution of \(\frac{d y}{d x}\) = 2^y-x. (2)
Answer:
We have.
(4x + 6y + 5)dx – (3x + 2y + 4)dy = 0

The given differential equation is not homogeneous.
OR

⇒ -2^y + 2^-x = c log 2
⇒ 2^-x – 2^y = k where k = c Log 2
Hence, the required solution is 2^-x – 2^y = k.

Question 3.
Find a unit vector in the direction of \(\overrightarrow{\mathrm{PQ}}\), where P and Q have coordinates (5, 0, 8) and (3, 3, 2) respectively. (2)
Answer:
We have, position vector of P = \(\overrightarrow{\mathrm{OP}}\) = 5î + 8k̂
and the position vector of Q = \(\overrightarrow{\mathrm{OQ}}\) = 3î + 3ĵ + 2k̂
\(\overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}}\)
= (3î + 3ĵ + 2k̂) – (5î + 8k̂)
= -2î + 3ĵ – 6k̂

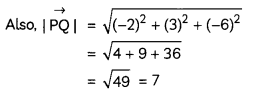
Now, unit vector in the direction of vector \(\overrightarrow{\mathrm{OP}}\)
= \(\frac{\overrightarrow{\mathrm{PQ}}}{\overrightarrow{\mid \mathrm{PQ}} \mid}\)
= \(\frac{1}{7}\)(-2î + 3ĵ – 6k̂)

Question 4.
Let \(\vec{a}\) and \(\vec{b}\) be two vectors such that |\(\vec{a}\)| = 3 and |\(\vec{a}\)| = \(\frac{\sqrt{2}}{3}\) Show that will be a unit vector, if the angle between them is \(\frac{\sqrt{2}}{3}\). (2)
Answer:
Let θ be the angle between the given two vectors \(\vec{a}\) and \(\vec{b}\).

Question 5.
Two dice are thrown. Find the probability that the numbers shown have a sum of 8, if it is known that the second die always exhibits 4. (2)
Answer:
Let A be the event of “occurrence of 4 always on second die” and B be the event of “occurrence of such numbers on both the dice whose sum is 8”.
∴ A = {(1,4), (2, 4), (3, 4), (4, 4), (5, 4), (6,4)}
And, B = {(2, 6), (3, 5), (4,4), (5, 3), (6, 2)}
∴P(A) = \(\frac{6}{36}=\frac{1}{6}\)
And P(B ∩ A) = \(\frac{1}{36}\)
Now,
Required Probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{1 / 36}{1 / 6}=\frac{1}{6}\)

Question 6.
Two dice are rolled simultaneously. Find whether the following two events, are independent or not:
E = {(x, y): x + y = 11}; F = {(x, y): x ≠ 5} (2)
Answer:
We have,
E = {(x, y) : x + y = 11
∴ E = {(5, 6), (6, 5)}
Also, F = {(x, y) : x ≠ 5}
∴ F = {(1, 1), (1, 2), (1, 3),(1, 5), (1, 6), (2,1), (2, 2), (2, 4), (2, 5), (2, 6), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} – {(5, 1), (5, 2), (5, 3) (5, 4), (5,5), (5, 6)}
n (E) = 2. n (F) = 30, n (E ∩ F) = 1

And,
P(E) = \(\frac{2}{36}=\frac{1}{18}\)
P(F) = \(\frac{30}{36}=\frac{5}{6}\)
and P(E ∩ F) = \(\frac{1}{36}\)

= P(E) × P(F)= \(\frac{1}{18} \times \frac{5}{6}=\frac{5}{108}\)
Since. P(E) × P(E) ≠ P(E ∩ F)
So, the two events E and F are not independent.

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
If ∫_a^bx³ dx = 0 and ∫_a^b x² dx = \(\frac{2}{3}\) Values of a and b.
OR
∫₁^ex³ logx dx (3)
Answer:

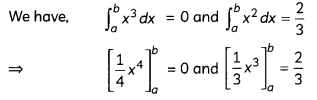
⇒ b⁴ – a⁴ = 0 and b³ – a³ = 2
Now, b⁴ – a⁴ = 0
⇒ (b² – a²)(b² + a²) = 0
⇒ (b – a) (b + a) (b² + a²) = 0
⇒ (b + a) (b² + a²) = 0 [∵ b ≠ a]
⇒ (b + a) = 0 [∵ b² + a² = 0]
⇒ a = -b
Substituting these values in b³ – a³ = 2, we get
a = -1,b = 1
OR
Let I = ∫₁^ex³ logx dx
= ∫₁^ex³ 1. logx dx
= log x∫1.dx – ∫[\(\frac{d}{d x}\)(log x).∫1dx]dx
(By Integration b parts formula)

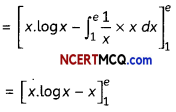
= (e.log e – e) – (1 log 1 – 1)
= (e – e) – (0 – 1)
= 1

Question 8.
Find the cartesian equation of a line passing through (1, 2, 3) and parallel to the line \(\frac{x+2}{-1}=\frac{y+3}{7}=\frac{2 z-6}{3}\). (3)
Answer:
Given equation of line can be rewritten as
\(\frac{x+2}{-1}=\frac{y+3}{7}=\frac{2 z-6}{3}\)

∴ Its direction ratios: (-1, 7, \(\frac{3}{2}\))

Since, required line is parallel to the given line, so their direction ratios will be proportional.
∴ Direction ratios of required line = (-λ, 7λ, \(\frac{3}{2}\)λ)

Also the required line passes through the point (1, 2, 3).
∴ Cartesian equation of the required line is:

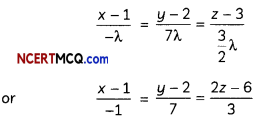
Question 9.
Solve the differential equation:
sin^-1\(\left(\frac{d y}{d x}\right)\) = x + y
OR
Solve the differential equation: du
tan x\(\frac{d y}{d x}\) + 2y = secx (3)
Answer:
Given differential equation can be rewritten as:
\(\frac{d y}{d x}\) = sin (x + y) …(i)
Put (x + y) = t

Differentiating w.r.t. x, we get
1 + \(\frac{d y}{d}=\frac{d t}{d}\)

Substituting these values in eq. (i), we get
\(\frac{d t}{d x}\) – 1 = sin t

⇒ \(\frac{d t}{d x}\) = 1 + sin t
or
\(\frac{d x}{d t}=\frac{1}{1+\sin t}\)
= \(\frac{1-\sin t}{\cos ^{2} t}\)
= (sec²t – tan t sec t)
⇒ dx = (sec²t -tan t sec t) dt

Integrating both sides, we get
∫dx = ∫ (sec² t – tan t sec t)dt
⇒ x = tan t – sec t + C
or, x = tan(x + y) – sec(x + y) + C
which is the required solution of the given differential equation.
OR
The given differential equation can be rewritten as:
\(\frac{d y}{d x}\) + 2cotx.y = cose cx

It is a linear differential equation in the form
\(\frac{d y}{d x}\) + P(x).y = Q(x) dx
where, P(x) = 2 cot x and Q(x) = cosec x

Integrating Factor (I.F.)
= e^∫P(x).dx
= e^{∫cot x.dx}
= e^2logsinx
= e^logsin2x
= sin² x

Thus, the solution to the given differential equation is:
y – (I.F.) = ∫Q(x).(I.F.)dx
⇒ y.sin²x= ∫ cosec x.sin2x dx
⇒ y .sin²x = ∫ sinx dx
⇒ y sin² x = – cos x + C
or y sin²x + cos x = C,
which is the required solution of the given differential equation.

Question 10.
Find the distance between the parallel planes \(\vec{r}\).(2î – 3ĵ + 6k̂) = 5 and \(\vec{r}\).(6î – 9ĵ + 18k̂) + 20 = 0. (3)
Answer:
Let \(\overrightarrow{r_{1}}\) be the position of any point on the plane \(\vec{r}\).(2î – 3ĵ + 6k̂) = 5
Then, \(\overrightarrow{r_{1}}\).(2î – 3ĵ + 6k̂) = 5
or \(\overrightarrow{r_{1}}\).(6î – 9ĵ + 18k̂) = 15

Now, the length of the perpendicular from \(\overrightarrow{r_{1}}\) to the other plane \(\vec{r}\).(6î – 9ĵ + 18k̂) + 20 = 0

Thus, the distance between the given parallel planes is \(\frac{5}{3}\) units.

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
Evaluate ∫₀^asin^-1\(\sqrt{\frac{x}{a+x}}\)dx. (4)
Answer:
Let I = ∫₀^asin^-1\(\sqrt{\frac{x}{a+x}}\)dx.
Put x = a tan² t
⇒ dx = 2a tan t sec² t dt

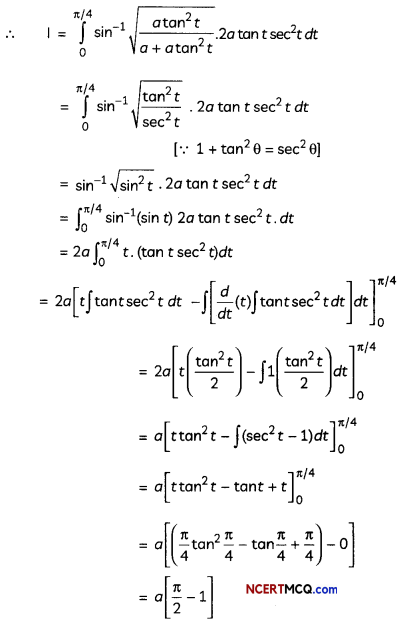
Question 12.
Using integration, find the area of the region bounded by a triangle whose vertices are A(2, 0), B(4, 5), C(6, 3).
OR
Sketch the bounded region and find the area bounded by the curve x = √y, the line x – y + 2 = 0 and the y-axis. (4)
Answer:
Given points are A(2, 0), B(4, 5) and C(6, 3).
We know, equation of a line with two given points, namely, (x₁, y₁) and (x₂, y₂) is given as:
y – y₁ = \(\left(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\right)\)(x – x₁)

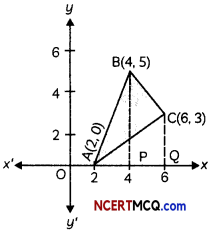
Equation of side AB of triangle ABC is:
y – 0 = \(\frac{5-0}{4-2}\)(x – 2)
⇒ 2y = 5x – 10

Equation of side BC of triangle ABC is:
y – 5 = \(\frac{3-5}{6-4}\)(x – 4)
⇒ y = 9 – x

Equation of side AC of triangle ABC is:
y – 0 = \(\frac{3-0}{6-2}\)(x – 2)
⇒ 4y = 3x – 6

Now, required area of ∆ABC = ar(region APBA) + ar(region BPQB) – ar(region AQCA)

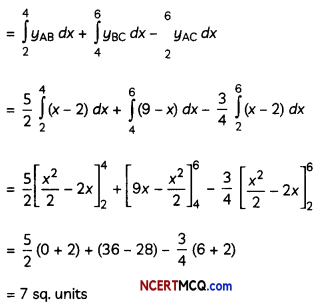
OR
x = √y, or x² = y is an equation of a parabola which open upwards with its vertex at origin.
To find the point of intersection of x² = y and x – y + 2 = 0, put y = x + 2 in x² = y.
∴ x² = x + 2
⇒ x² – x – 2 = 0
⇒ (x – 2) (x + 1) = 0
⇒ x = 2, -1
For x = 2, y = 4
For x = -1, y = 1
∴ Points of intersection are (2, 4) and (-1, 1). Also, the area common to the curve x² = y, line y = x + 2 and the y-axis is shown shaded in the figure.

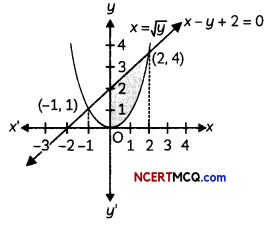
Question 13.
A bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that at least one of the three marbles drawn be black, if the first marble is red? (4)
Answer:
Here, R = red marble and B = black marble For the condition that at least one of the three marbles drawn be black, if first marble is red, then following are the possibilities:
(A) Second marble is black and third is red (E₁)
(B) Second marble is black and third is also black (E₂)
(C) Second marble is red and third is black (E₃)

Case-Based/Data-Based

Question 14.
Three slogans on chart paper are to be placed on a school bulletin board at the points A, B and C displaying A, B and C The coordinates
of these points are A(2. 5, 1),B(3, – 3, 2)and C(- 2, 4, 7) respectiveLy. Let \(\vec{a}, \vec{b}\) and \(\vec{c}\) be the position vectors of A, B, and C respectively

Based on the above information, answer the following two questions:
(A) Find the unit vector in the direction of \(\vec{b} \times \vec{c}\) (2)
Answer:
Here,
\(\vec{b} \times \vec{c}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
3 & -3 & 2 \\
-2 & 4 & 7
\end{array}\right|\)
= (- 21 – 8)î – (21 + 4)ĵ + (12 – 6)k̂
= – 29î – 25ĵ + 6k̂
So, unit vector in the direction of \(\vec{b} \times \vec{c}\)

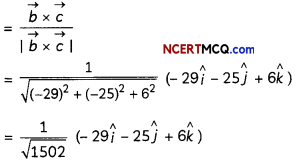
(B) Find the area of ∆ABC. (2)
Answer:
Area of ∆ABC = \(\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|\)
Now, \(\overrightarrow{A B}\)=(3 – 2)î + (-3 – 5)ĵ + (2 – 1)k̂
= î – 8ĵ + k̂
and \(\overrightarrow{A C}\) =(-2 – 2)î + (4 – 5) ĵ+(7 – 1)k̂
= -4î – ĵ + 6k̂