CBSE Sample Papers for Class 12 Maths Term 2 Set 7 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 7 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 7 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
The direction cosines of a line segment AB are \(\frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}\) If AB = \(\sqrt{17}\) and the coordinates of A are (3, -6, 10), then find coordinates of B. (2)
Answer:
Since, direction cosines of AB are \(\frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}\)
So, direction ratios of the Line AB are < -2, 3, -2>.
DR of the line AB = Coordinates of B – coordinates A
Let the coordinates of B be (x, y, z).
So, direction ratios of AB = <x – 3, y + 6, z – 10>
⇒ <-2, 3, -2> = <x – 3, y + 6, z – 10>
⇒ x – 3 = -2; y + 6 = 3; z – 10 = -2
⇒ x = 1; y = -3; z = 8
Thus, coordinates of B are (1, -3, 8).

Question 2.
A die is rolled. If the outcome is an even number, what is the probability that it is a prime number?
OR
A player has 7 cards in hand of which 5 are red and among these five, 2 are kings. A card is drawn at random. Find the probability that it is a king, if being known that it is red. (2)
Answer:
Sample space, S = { 1, 2, 3, 4, 5, 6}
Let A be the event of “getting an even number”, and B be the event of “getting a prime number”,
n (A) = {2, 4, 6}, n(B) = {2}, n (B ∩ A) = {2}
P(A) = \(\frac{3}{6}=\frac{1}{2}\)
And, P(B ∩ A) = \(\frac{1}{6}\)
[∵ 2 is the only even prime number from 1 to 6]
Now,
Required probability = P(B/A)
\(\frac{P(B \cap A)}{P(A)}=\frac{1 / 6}{1 / 2}=\frac{1}{3}\)

OR
Let A be the event of “card being red”, and B be the event of “card being king”.
P(A) = \(\frac{5}{7}\) And P(B ∩ A) = \(\frac{2}{7}\)
Now, required probability = P(B/A)
= \(\frac{P(B \cap A)}{P(A)}\)
= \(\frac{2 / 7}{5 / 7}=\frac{2}{5}\)

Question 3.
Find the vector and the cartesian equations of a line passing through the points (3, -2,-5) and (3, – 2, 6). (2)
Answer:
The direction ratios of the line passing through the points (3, -2, – 5) and (3, -2, 6) are (3 – 3, – 2 + 2, 6 + 5) i.e., (0, 0, 11).
Also, the required line passes through the point (3,-2,-5).
So, the cartesian equation of the required line is

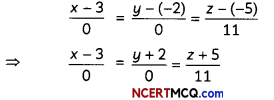
And, its vector equation is
\(\vec{r}\) = (3î – 2ĵ – 5k̂) + λ(11k̂)

Question 4.
Evaluate ∫₀²| 1 – x | dx. (2)
Answer:

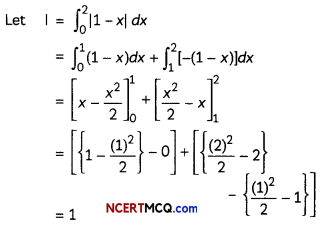
Question 5.
A die marked 1,2,3 in red and 4,5,6 in green is tossed. Let A be the event “the number is even” and B be the event “the number is red”. Are A and B independent? Give reasons for your answer. (2)
Answer:
We have, A = Event that the number is even.
∴ A = {2, 4, 6}
P(A) = \(\frac{3}{6}=\frac{1}{2}\)

Also, B = Event that the number is red.
∴ B = {1, 2, 3}
P(B) = \(\frac{3}{6}=\frac{1}{2}\)

And, A ∩ B = event that number is even and red
⇒ A ∩ B = {2}
P(A ∩ B) = \(\frac{1}{6}\)

∵P(A) × P(B) = \(\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}\) ≠ P(A n B)
Hence, the two events A and B are not independent.

Question 6.
Sketch the region bounded by curves y = x² and y = |x|. (2)
Answer:

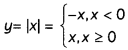
Hence, y = x² is an equation of parabola which open upwards, towards positive side of y-axis, with its vertex at the origin.

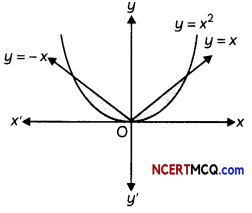
Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Find the area of the region bounded by the curve y² = 4x, the lines x = 1 and x = 4 and the x-axis in the first quadrant.
OR
Find the area of the region bounded by the curve y = |x + 3|, the lines x = -6 and x = 0. (3)
Answer:
y² = 4x represents a parabola whose vertex is at the origin, axis of symmetry is x-axis, focus on the positive direction of x-axis and it opens to the right

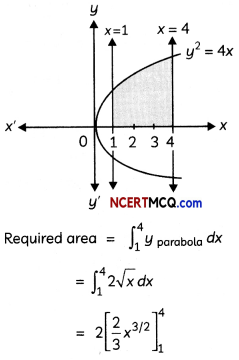
= \(\frac{4}{3}\)[(4)^3/2 – (1)^3/2]
= \(\frac{4}{3}\)(8 – 1)
= \(\frac{28}{3}\) sq.units
OR
We have, y = |x + 3|

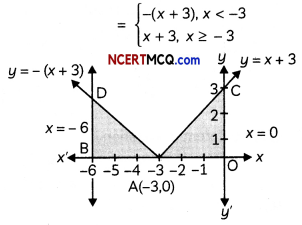
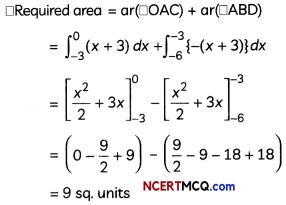
Question 8.
Find the area of a parallelogram whose adjacent sides are determined by vectors \(\vec{a}\) = î – ĵ + 3k̂ and b = 2î – 7ĵ + k̂ respectively. (3)
Answer:
Let ABCD be the parallelogram with \(\overrightarrow{\mathrm{AB}}=\vec{a}\) = î – ĵ + 3k̂ and \(\overrightarrow{\mathrm{BC}}=\vec{b}\) = 2î – 7ĵ + k̂.

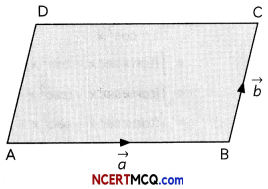
∴ Area of Parallelogram ABCD = \(|\overrightarrow{A B} \times \overrightarrow{B C}|\)
Now,
\(\overrightarrow{A B} \times \overrightarrow{B C}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -1 & 3 \\
2 & -7 & 1
\end{array}\right|\)
= î(-1 + 21) – ĵ(1 – 6) + k̂(-7 + 2)
= 20î + 5ĵ – 5k̂

∴ \(|\overrightarrow{A B} \times \overrightarrow{B C}|=\sqrt{(20)^{2}+(5)^{2}+(-5)^{2}}\)
= \(\sqrt{450}\)
= 15√2

Question 9.
Evaluate ∫₀² x\(\sqrt{2-x}\)dx.
OR
Evaluate ∫\(\frac{\sin x}{1+\sin x}\) dx. (3)
Answer:
Let I = ∫₀² x\(\sqrt{2-x}\)dx.
Put 2 – x = t
⇒ -dx = dt
For x= 0, t= 2 – 0 = 2
For x = 2, t= 2 – 2 = 0

OR
Let I = ∫\(\frac{\sin x}{1+\sin x}\) dx
= ∫\(\frac{\sin x(1-\sin x)}{1-\sin ^{2} x}\)dx
= ∫\(\frac{\sin x-\sin ^{2} x}{\cos ^{2} x}\) dx
= ∫(tan x sec x – tan² x)dx
= ∫[tan x sec x – (sec² x – 1)] dx
= ∫(tan x sec x – sec² x + 1)dx
= sec x – tan x + x + C

Question 10.
Let \(\vec{a}, \vec{b}, \vec{c}\) be the three vectors such that | \(\vec{a}\) | = 3, | \(\vec{b}\) | = 4 and | \(\vec{c}\) | = 5 and each one of them being perpendicular to the sum of the other two. Find | \(\vec{a}+\vec{b}+\vec{c}\) |. (3)
Answer:
It is given that each vector is perpendicular to the sum of other two vectors.

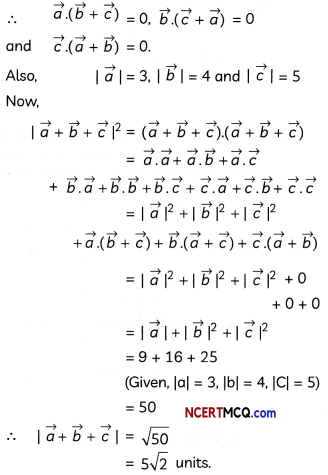
Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
Four defective bulbs are accidentally mixed with six good ones. If it is not possible to just look at a bulb and tell whether or not it is defective, then find the probability distribution of the number of defective bulbs, if four bulbs are drawn (without replacement) at random from this lot. (4)
Answer:
Let X be the discrete random variable defined as the number of defective bulbs.
Then, X can take values 0,1, 2, 3, 4.
Now, P(X = 0) = P (all the bulbs are good ones)

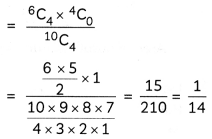
P(X = 1) = P(1 defective and three good ones)

P(X = 2) = P(2 defective and two good ones)

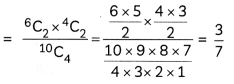
P(X = 3) = P(3 defective and one good one)

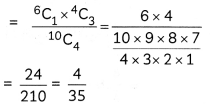
P(X = 4)= P (All the four defective bulbs)

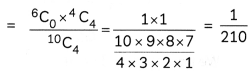
Thus, the probability distribution of X is

Question 12.
Solve the differential equation:
\(\frac{d y}{d x}=\frac{x+y+7}{2 x+2 y+3}\)
OR
Solve the differential equation: du
sin x \(\frac{d y}{d x}\) + y cos x = x sin x
Answer:
Given differential equation is:
\(\frac{d y}{d x}=\frac{x+y+7}{2 x+2 y+3}\) …(i)

Put (x + y + 7) = z
⇒ 1 + \(\frac{d y}{d x}=\frac{d z}{d x}\)
Substituting these values in (i), we get

where, C₁ = 9C
or, 6y – 3x – 11 log (3x + 3y + 10) = C₂, where
C₂ = C₁ – 42.

which is the required solution of the given differential equation.
OR
The given differential equation can be rewritten dy
as \(\frac{d y}{d x}\) + cotx.y = x dx

It is a linear differential equation in the form
\(\frac{d y}{d x}\) + P(x).y = Q(x) dx
where, P(x) = cot x and Q(x) = x

Integrating Factor (I.F.) = e^∫Pdx
= e^{∫cot x dx}
= e^{logsin x}
= sin x

Thus, the solution to the given differential equation is:
y.(I.F.) = ∫Q(x).(I.F.)dx
⇒ y.sin x = ∫x.sin x dx
⇒ y.sin x = x∫sin x dx – ∫[\(\frac{d y}{d x}\)(x)∫sin xdx]dx
⇒ y. sin x = -x cos x + sin x +C
⇒ y. sin x + x cos x = sin x + C
which is the required solution of the given differential equation.

Question 13.
Evaluate ∫cos{2 cot^-1\(\sqrt{\frac{1-x}{1+x}}\)}dx. (4)
Answer:
Let I = ∫cos{2 cot^-1\(\sqrt{\frac{1-x}{1+x}}\)}dx.
Put x = cos t
⇒ dx = -sin t dt
I = -∫cos{2 cot^-1\(\sqrt{\frac{1-\cos t}{1+\cos t}}\)}sin tdt

CASE-BASED/DATA-BASED

Question 14.
Rohan and Rohit are two friends, and they are going to a road trip on their motorcycles. Their motorcycles are running at the speed more than the allowed speed on the road along the lines \(\vec{r}\) = λ(î + 2ĵ – k̂) and \(\vec{r}\) = 3î + 3ĵ + μ(2î + ĵ + k̂) respectively.

Based on the above information, answer the following two questions:
(A) Find the direction ratios of the line along which (i) motorcycle A is running (ii) motorcycle B is running. (2)
(B) Find the shortest distance between the two lines. (2)
Answer:
(A) (i) Direction ratios of the line along which the motorcycle A is running are <1, 2, – 1>.
(ii) Direction ratios of the line along which the motorcycle B is running are <2, 2, 1>.

(B) On comparing the given equations with equations \(\vec{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\) and \(\vec{r}=\overrightarrow{a_{2}}+\lambda \overrightarrow{b_{2}}\)
we have
\(\overrightarrow{a_{1}}=\overrightarrow{0}\)
b₂ = î + 2î – k̂
\(\overrightarrow{a_{2}}\) = 3î + 3î
b₂ = 2i + ĵ + k̂