CBSE Sample Papers for Class 12 Maths Term 2 Set 8 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 8 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 8 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Evaluate

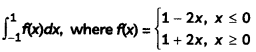
Answer:
Let

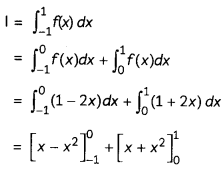
= [0 – (-1 – 1)] + [(1 + 1) – 0]
= 2 + 2
= 4

Question 2.
Identify the functions P(x) and Q(x) from the linear differential equation (tan^-1 x – y) dx = (1 + x²) dy.
Or
Solve the differential equation \(\frac{d y}{d x}\) + 1 = e^x+y
Answer:
We have

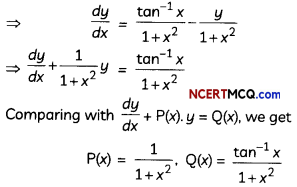
Given, differential equation is
\(\frac{d y}{d x}\) + 1 = e^x+y ….(i)
Let x + y = t
On differentiating w.rt x, we get
1 + \(\frac{d y}{d x}=\frac{d t}{d x}\) ….(ii)

∴ From equation (i) and (ii),
\(\frac{d y}{d x}\) = e^x
⇒ e^-tdt = dx
On integrating both sides, we get
⇒ \(\frac{-e^{-t}}{e^{x+y}}\) = x + c
⇒ -1 = (x + c)e^x+y
⇒ (x + c)e^x+y = 0

Caution:
Do the necessary substitution. wherever needed.

Question 3.
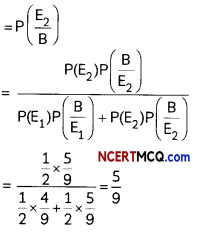
Urn I contains 5 white and 4 blue balls. Urn II contains 4 white and 5 blue balls. One of the urn is selected at random and a ball is drawn from it. If the ball drawn is blue, what is the probability that it is drawn from Urn II? (2)
Answer:
Let E₁ and E₂ be the events of selecting Urn I
and Urn II respectively,
Also, let B be the event of drawing a blue ball
∴ P(E₁) = \(\frac{1}{2}\) and P(E₂) = \(\frac{1}{2}\)
Also, P = \(\left(\frac{B}{E_{1}}\right) \frac{4}{9}\) and P = \(\left(\frac{\mathrm{B}}{\mathrm{E}_{2}}\right) \frac{5}{9}\)

Using Bayes Theorem,
Required Probability

Question 4.
Find the intercepts made on the coordinate axes by the plane x + 2y – 2z = 9. Also, find the direction cosines of the normal to the plane. (2)
Answer:
Given Equationsof plane is:
x +2y – 2z = 9
Or
\(\frac{x}{9}+\frac{2 y}{9}-\frac{2 z}{9}\) = 1
Or
\(\frac{x}{9}+\frac{y}{\frac{9}{2}}+\frac{z}{\frac{-9}{2}}\) = 1

Thus, the intercepts made by the plane on the coordinate axes are 9, \(\frac{9}{2},-\frac{9}{2}\) respectively.
Now, direction ratios of the normal to the plane are (1, 2, -2).
Therefore, direction cosines of the normal to the plane

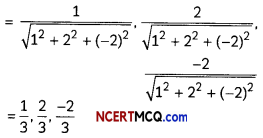
Question 5.
Two cards are drawn successively with replacement from a well-shuffled pack of 52 playing cards. Find the probability distribution of the number of queens. (2)
Answer:
Let X denotes the discrete random variable “the number of queens”. When two cards are drawn with replacement.
Then, X takes values 0,1, 2.
P(X = 0) = P(both cards are not queen)
= \(\frac{48}{52} \times \frac{48}{52}=\frac{144}{169}\)
P(X = 1) = P(one card is queen)
= \(\frac{4}{52} \times \frac{48}{52}+\frac{48}{52} \times \frac{4}{52}=\frac{24}{169}\)
P(X = 2) = P(both are queen cards)
= \(\frac{4}{52} \times \frac{4}{52}=\frac{1}{169}\)

So, the required probability distribution of X is

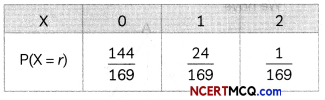
Question 6.
The dot products of a vector with the vectors î + ĵ – 3k̂, î + 3ĵ – 2k̂ and 2î + ĵ + 4k̂ are 0, 5 and 8 respectively. Find the vector. (2)
Answer:
Let the required vector be
\(\vec{a}\) = αî + βĵ + γk̂

Then, according to the question,
(αî + βĵ + γk̂). (î + 3ĵ – 2k̂) =0
⇒ α + 3β – 2γ = 5 …(ii)
and, (αî + βĵ + γk̂) ,(2î + ĵ + 4k̂) = 8
⇒ 2α + β + 4γ = 8 …(iii)
Solving equation (i), (ii) and (iii) we get
Thus, the required vector is î + 2ĵ + k̂

Section – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Evaluate ∫\(\frac{\sin 4 x}{\sin x}\)dx.
or
Evaluate ∫₀⁹ f(x) dx. (3)

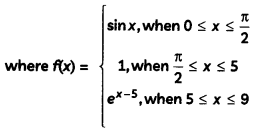
Answer:
Let I = ∫\(\frac{\sin 4 x}{\sin x}\)dx.
= ∫\(\frac{2 \sin 2 x \cos 2 x}{\sin x}\) dx
[∵ sin 2θ = 2 sin θ cos θ]
= ∫\(\frac{2(2 \sin x \cos x) \cos 2 x}{\sin x}\) dx
= 4∫cos x cos 2x dx
= 4∫cos x(1 – 2 sin²x)dx
[∵ cos 2x = 1 – 2 sin²x]

Put sin x = t
⇒ cos x dx = dt
∴ I = 4∫(1 – 2t²) dt

Question 8.
A(-4, 7, 2),B(2, -5, 8) and C(-5, -1, 5) are three points. Find the equation of the line AB. If D is the foot of the perpendicular drawn from the point C to the Line AB, find the coordinates of D. (3)
Answer:
Equation of Line AB is

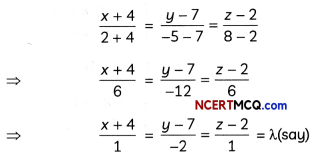
∴ Any point on this line is (λ – 4, – 2λ + 7, λ + 2).

Let it be the point D and is the foot of the perpendicular from C (-5, – 1, 5) on the line AB.
Now, direction ratios of CD = (λ, – 4 + 5, – 2λ + 7 + 1, λ + 2 – 5)
= {λ + 1, – 2λ + 8, λ – 3}

Since, CD is perpendicular to AB.
∴ (λ + 1) × 1 + (- 2λ + 8) × (- 2) + (λ – 3) × 1 = 0
⇒ 6λ – 18 = 0
⇒ λ = 3
Thus, the coordinates ofthe point Dare (3 – 4, -2 × 3 + 7, 3 + 2), i.e., (- 1, 1, 5).

Related Theory
Two lines with directions ratios a₁, b₁, c₁ and a₂, b₂, c₂ are perpendicular, if a₁a₂ + b₁b₂ + c₁c₂ = 0

Question 9.
Find the area of the region bounded by the curve y = |x – 5| and the Lines x = 0 and x = 1.
Or
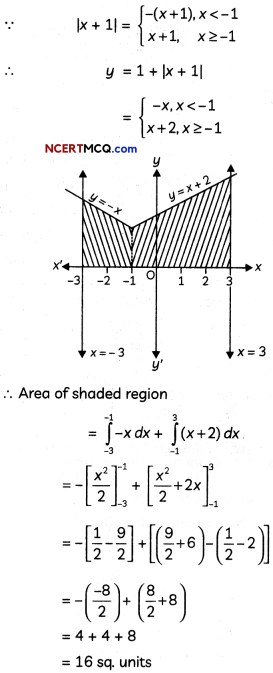
Draw a rough sketch of the curve y = 1 + |x + 1|, x = -3, x = 3, y = 0 and find the area of the region bounded by them, using integration. (3)
Answer:
We have, y = |x – 5|

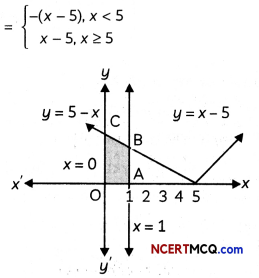
∴ Required area = ar(region OABC)

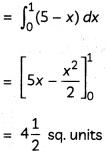
Given curves are y = 1 + |x + 1|, x = -3, x = 3 and y = 0

Question 10.
Using vectors show that the median of an isosceles triangle is perpendicular to the base. (3)
Answer:
Let ABC be an isosceles triangle with AB = AC.
Let the position vectors of B and C taking A as origin be \(\vec{b}\) and \(\vec{c}\).

We have,

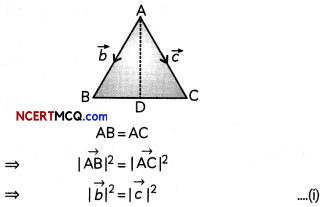
Since, AD is median of ∆ABC
∴ D bisect the base BC
∴ Using mid-point formula,

So, angle between \(\overrightarrow{A D}\) and \(\overrightarrow{B C}\) is \(\frac{π}{2}\)
Thus, AD is perpendicular to BC.
Hence proved.

Section – C
(Section – C has 4 long answer type questions (LA) of 4 marks each.)

Question 11.
If y(x) is a solution of \(\left(\frac{2+\sin x}{1+y}\right)\) = -cos x and y(0) = 1, then find the value of y \(\frac{π}{2}\).
Answer:
Given \(\left(\frac{2+\sin x}{1+y}\right)\) = -cos x
⇒ \(\frac{d y}{1+y}=-\left(\frac{\cos x}{2+\sin x}\right)\)dx

On integrating both sides, we get cosx
∫\(\frac{1}{1+y}\)dy = -∫\(\frac{\cos x}{2+\sin x}\)dx
⇒ log(1 + y) = -log(2 + sin x) + log c
⇒ log(1 + y)(2 + sin x) = log c
⇒ (1 + y)(2 + sin x) = c

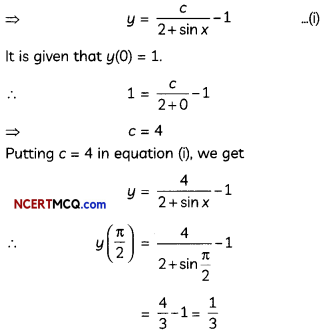
Question 12.
Two dice are thrown together and the total score is noted. The events E, F and G are “a total of 4”, “a total of 9 or more” and “a total which is divisible by 5” respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.
Or
A bag contains 2 red and 3 black balls. Find the probability distribution of the number of red balls, if 4 balls are drawn out (i) with replacement from the bag. (ii) without replacement from the bag. (4)
Answer:
We have,
F = (3, 6), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 3), (6, 4), (6, 5), (6, 6)
G = (1, 4), (2, 3), (3, 2), (4,1), (4, 6), (5, 5), (6, 4)

∴ P(E) = \(\frac{3}{36}=\frac{1}{12}\)
P(F) = \(\frac{10}{36}=\frac{5}{18}\)
P(G) = \(\frac{7}{36}\)

Further, E ∩ F = Φ, E ∩ G = Φ and F ∩ G = {(4, 6), (5, 5), (6, 4)}
P(E ∩ F) = 0, P(F ∩ G) = \(\frac{3}{36}=\frac{1}{12}\)

Now, P(E) × P(F) = \(\frac{1}{12} \times \frac{5}{18}\)
= \(\frac{5}{216}\) ≠ P(E ∩ F)
⇒ E and F are not independent.

P(E) × P(G) = \(\frac{1}{12} \times \frac{7}{36}\)
= \(\frac{7}{432}\) ≠ P(E ∩ G)
⇒ E and G are not independent.

P(F) × P(G) = \(\frac{5}{18} \times \frac{7}{36}\)
= \(\frac{35}{648}\) ≠ P(F ∩ G)
⇒ E and G are not independent.
Thus, event E, F and G are not pair-wise independent.

Or

(i) Let X be the discrete random variable defined as the number of red balls, when four ball are drawn with replacement.
Then, X can take values 0,1, 2, 3, 4.
Now, ‘
P(X = 0) = P(allfour balls are black)
\(\frac{3}{5} \times \frac{3}{5} \times \frac{3}{5} \times \frac{3}{5}=\frac{81}{625}\)
P(X = 1) = P(1 red ball and 3 black balls)
= P(first ball is red and next three balls are black) + P(second ball is red and rest are black balls) + P(third ball is red and rest are black balls) + P(fourth ball is red and rest are black balls)

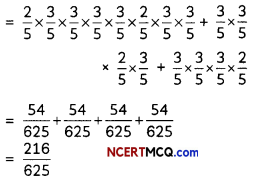
P(X = 2) = P(2 red balls and 2 black balls)
= P(first two are red balls, next two balls are black) + P(First, third ball are red) + P(second, fourth ball are red) + P(last two balls are red) + P(First, fourth balls are red) + P(second, third balls are red)

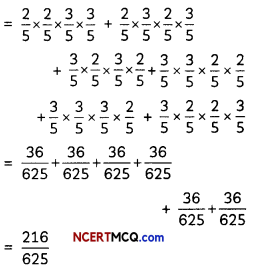
P(X = 3) = P(3 red balls and 1 black ball)
= P(first three balls are red) + P(second ball is black) + P(first ball is black) + P(third ball is black)

P(X = 4) = P(All four balls are red)
= \(\frac{2}{5} \times \frac{2}{5} \times \frac{2}{5} \times \frac{2}{5}=\frac{16}{625}\)

Thus, the probability distribution of X is:

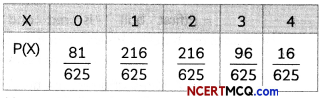
(ii) Let X be the discrete random variable defined as the number of red balls, when four balls are drawn without replacement.
Then, X can take values 1, 2
P(X = 1) = P(1 red ball and 3 black balls)
= \(\frac{{ }^{2} C_{1} \times{ }^{3} C_{3}}{{ }^{5} C_{4}}=\frac{2 \times 1}{5}=\frac{2}{5}\)

P(X = 2) = P(2 red balls and 2 black balls)
= \(\frac{{ }^{2} C_{2} \times{ }^{3} C_{2}}{{ }^{5} C_{4}}=\frac{1 \times 3}{5}=\frac{3}{5}\)

Thus, the probability distribution of X is

Caution:
In part (ii). X cannot take O i.v1ue os there ore total of 3 block 1 and 2 red balls So on drawing four baILš. without replacement one of them wilt definitely be red.

Question 13.
Evaluate ∫x(logx)²dx. (4)
Answer:
Let I = ∫x(logx)²dx

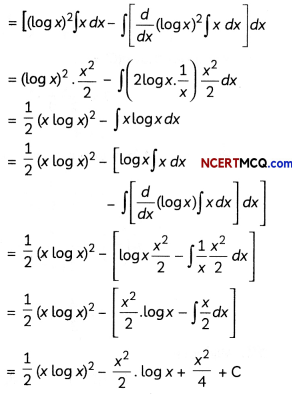
Case-Based/Data-Based

Question 14.
Ranjana’s house is situated at Roop Nagar at point O. For going to Nita’s house, she first travels 10 km by bus in the East. Here at point A, a hospital is situated. From hospital, Ranjana takes an auto and goes 8 km in the North. Here at point B, a school is situated. From school, she travels by bus to reach Nita’s house at point C, which is at 30° East 12 km from point B.

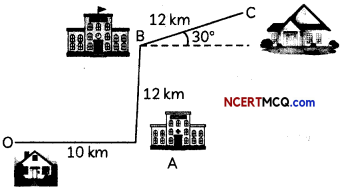
Based on the above information, answer the following two questions:
(A) What is the vector distance between Ranjana’s house and school? (2)
(B) What is the vector distance from school to Nita’s house? (2)
Answer:
(A) Required distance, \(\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AB}}\)
[Using triangle law of vector addition]
= 10î + 8ĵ

(B) Required distance = \(\overrightarrow{\mathrm{BC}}\)

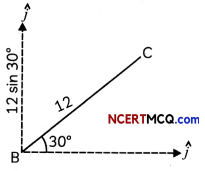
12 cos 30° î + 12 sin 30°ĵ = 12 × \(\frac{\sqrt{3}}{2}\)î + 12 × \(\frac{1}{2}\)ĵ
= 6√3 î + 6ĵ