CBSE Sample Papers for Class 12 Maths Term 2 Set 9 with Solutions

Students can access the CBSE Sample Papers for Class 12 Maths with Solutions and marking scheme Term 2 Set 9 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Maths Term 2 Set 9 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• This question paper contains three sections-A. B and C. Each part is compulsory.
• Section-A has 6 short answer type (SA1) questions of 2 marks each.
• Section-B has 4 short answer type (SA2) questions of 3 marks each.
• Section-C has 4 long answer type questions (LA) of 4 marks each.
• There is an Internal choice in some of the questions.
• Q14 is a case-based problem having 2 sub parts of 2 marks each.

Section – A
(Section – A has 6 short answer type (SA-1) questions of 2 marks each.)

Question 1.
Evaluate (2)

Answer:

Question 2.
Show that the solution of differential equation x dy – y dx = 0 represents a straight line.
OR
Write the general solution of the differential equation cos x sin y dx + sin x cos y dy = 0. (2)
Answer:
We have,
x dy – y dx = 0
or x dy = y dx
⇒ \(\frac{d y}{y}\) = \(\int \frac{d x}{x}\)
Integrating both sides, we get
⇒ \(\int \frac{d y}{y}\) = \(\int \frac{d x}{x}\)
⇒ log y = log x + log C,
where log C is constant of integration.
⇒ log y = log Cx
⇒ y = Cx
which is an equation of a straight line passing through the origin.
Hence proved.
OR
We have,
cos x sin y dx + sin x cos y dy = 0
or, cos x sin y dx = – sin x cos y dy
⇒ \(\frac{\cos x}{\sin x}\)dx = \(\frac{\cos y}{\sin y}\)dy
Integrating both sides, we get
\(\int \frac{\cos x}{\sin x}\) dx = –\(\int \frac{\cos y}{\sin y}\)dy
⇒ log |sin x| = – log |sin y| + log c [∵ \(\int \frac{f^{\prime}(x)}{f(x)}\)dx = log|f(x)| + C]
⇒ log (sin x. sin y) = log C
or, sin x sin y = C

Question 3.
For any two vectors \(\vec{a}\) and \(\vec{b}\), show that |\(\vec{a}\) + \(\vec{b}\)| ≤ |\(\vec{a}\)| + |\(\vec{b}\)|. (2)
Answer:
We have,

Question 4.
If |\(\vec{a}\)| = 10, |\(\vec{b}\)| = 2 and \(\vec{a} \cdot \vec{b}\) = 12, then find the value of \(|\vec{a} \times \vec{b}|\). (2)
Answer:

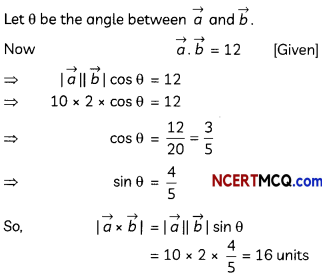
Question 5.
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is six. Find the probability it is actually a six. (2)
Answer:
Let E be the event that the man reports that six has occurred on throwing a die.
Also, let E₁ be the event “six has occurred” and E₂ be the event “six does not occurred”.
∴ P(E₁) = \(\frac{1}{6}\) and P(E₂) = \(\frac{5}{6}\)
Also,
P\(\left(\frac{E}{E_{1}}\right)\) = Probability that the man does not speaks truth = \(\frac{1}{4}\)
Now, using Bayes’ theorem,
Required probability = P\(\left(\frac{E_{1}}{E}\right)\)

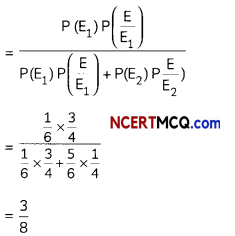
Question 6.
In answering a question on a multiple choice test, a student either knows the answer or guesses. Let \(\frac{3}{4}\) be the probability that he knows the answer and \(\frac{1}{4}\) be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability \(\frac{1}{4}\). What is the probability that the student knows the answer given that he answered it correctly? (2)
Answer:
Let E₁ be the event “the student knows the answer” and E₂ be the event “guesses the answer”.
Also, let A be the event “answer is correct”

Caution:
P\(\left(\frac{\mathrm{A}}{E_{1}}\right)\) = 1, as be knows the answer so his answer wili definitely be correct.

SECTION – B
(Section – B has 4 short answer type (SA-2) questions of 3 marks each.)

Question 7.
Evaluate \(\int \frac{x}{(x+2)(3-2 x)}\) dx.
OR
Evaluate (3)

Answer:

OR

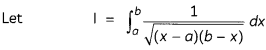
Put x = a cos² t + b sin² t
⇒ dx = a(2 cos t) (- sin t) dt + b(2 sin t cos t) dt
= 2(b – a) sin t cos t dt
Also, x – a = (b – a) sin² t
and b – x = (b – a) cos² t
when x = b, t = \(\frac{\pi}{2}\); and when x = a, t = 0

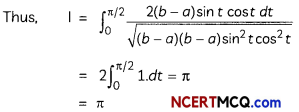
Question 8.
Find the equation of the plane passing through the points (2, 1, – 3), (- 3, – 2, 1) and (2, 4, -1). (3)
Answer:
We know that the equation of the plane passing through three points (x,₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) is given by:
\(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|\) = 0 …….. (i)
Here,
(x₁, y₁, z₁) = (2, 1, – 3)
(x₂, y₂, z₂) = (- 3, – 2, 1)
and (x₃, y₃, z₃) = (2, 4, – 1)
Substituting these values in (i), we get

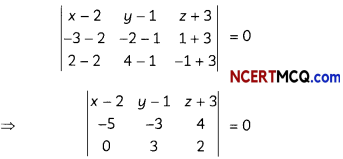
(x- 2) (- 6 – 12) – (y – 1) (- 10 – 0) + (z + 3) (- 15 + 0) = 0
⇒ 18 (x – 2) + 10(y – 1) – 15(z + 3) = 0
⇒ 18x + 10y – 15z – 19 = 0
Thus, the required equation of the p[ane is:
⇒ 18x + 10y – 15z – 19 = 0

Question 9.
Sketch the bounded region and find the area of the region bounded by the curve y = |x|, the x-axis and the ordinates x = -1 and x = 1.
OR
Find the area of the region bounded by the circle x² + y² = 4, the line x = √3y and the x-axis in the first quadrant. (3)
Answer:
Required area = ar(∆OAB) + ar(∆OCD)


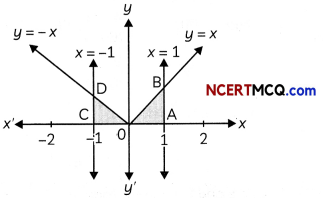
OR
x² + y² = 4 represents a circle with centre at the origin and radius √4 i.e., 2 units; and the line x = √3y passes through the origin.

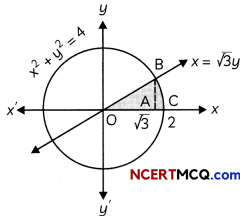
The line intersects the circle at point B (√3, 1) in the first quadrant.
∴ Required area = ar (∆OAB) + ar(region CAB)

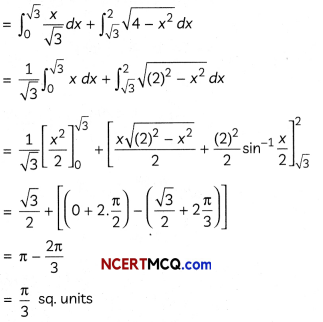
Question 10.
If AC and BD are the diagonals of a quadrilateral ABCD, then show that its vector area is given by \(\frac{1}{2}(\overrightarrow{A C} \times \overrightarrow{B D})\). (3)
Answer:
Vector area of quadrilateral ABCD = Vector area of ∆ABC + Vector area of ∆ACD

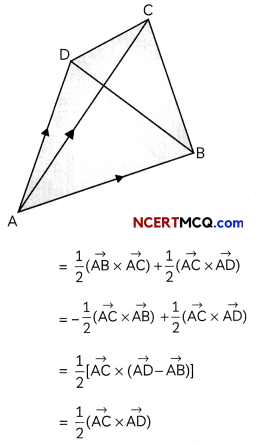
Using triangle law of vector addition in ∆ABD]
Hence proved.

Section – C
(Section – C has 4 Long answer type questions (LA) of 4 marks each.)

Question 11.
Evaluate \(\int x \sin ^{-1}\left\{\frac{1}{2} \sqrt{\frac{2 a-x}{a}}\right\}\) (4)
Answer:

Question 12.
Consider an experiment of throwing two dice. Let E denote the event “odd number on the first die”, F denote the event” odd number on the second die” and G denote the event “sum of numbers on two dice is odd”. Show that E, F and G are pairwise independent events, but not mutually independent. (4)
Answer:
We have,
E = {(1, 1), (1. 2), (1, 3), (1, 4), (1, 5) (1, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5,1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
F = [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3), (1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5)}
and G = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4,1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5)}
Further, E ∩ F = {(1,1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5,1), (5, 3), (5, 5)
E ∩G = [(1, 2), (1, 4), (1, 6), (3, 2), (3, 4), (3, 6), (5, 2), (5, 4), (5, 6)]
And F ∩ G = {(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}

⇒ E and G are independent.
Thus, E, F and G are pairwise independent events.
Hence proved.
Now,
E ∩ F ∩ G = Φ
P(E ∩ F ∩ G) = O
Also,
P(E) × P(F) × P(G) = \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\)
= \(\frac{1}{8}\) ≠ P(E ri Fri G)
Thus, E, F and G are not mutuatlly independent events.
Hence proved.

Question 13.
Show that the lines \(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\) and \(\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}\) are coplanar. Also,find the point of intersection. (4)
Answer:
Given lines are
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)
and \(\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}\)
If two lines are coplanar, then
\(\left|\begin{array}{ccc}
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2}
\end{array}\right|\) = 0
Here,
(x₁, b₁, c₁) = (1, 2, 3)
(a₁, b₁, c₁) = (2, 3, 4)
(x₂, y₂, z₂) = (2, 3,4)
(a₂, b₂, c₂) = (3, 4, 5)

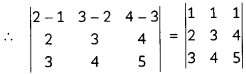
= 1(15 – 16) – 1(10 – 12) + 1(8 – 9)
= – 1 + 2 – 1 = 0
Hence, the given lines are coplanar.
Hence proved.
Now, any general point on the line
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\) = λ (say) is (2λ + 1, 3λ + 2, 4λ + 3)
Also, any general point on the line
\(\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}\) = µ(say) is (3µ + 2, 4µ + 3, 5µ + 4).
Since, the given two lines are coplanar, so they must be intersecting.
∴ 2λ + 1 = 3µ + 2;
3λ + 2 = 4µ + 3;
4λ + 3 = 5µ + 4
On solving these three equations, we get λ = – 1, µ = – 1.
Hence, the point of intersection of the given two lines is (- 1, – 1, – 1).

Related Theory:
Intersecting Lines are always coplanar.

CASE-BASED/DATA-BASED

Question 14.
The rate at which a body cools is proportional to the difference between the temperature of the body and that of the surrounding air. A body in air at 25°C will get cool from 100°C to 75°C in one minute.

Based on the above information, answer the following two questions:
(A) Find its temperature at the end of 3 minutes.
(B) After how many minutes, its temperature will be 58°C?
OR
The population of Swastik’s village increases continuously at the rate proportional to the number of its inhabitants present at any time. The population of the village was 20,000 in 1999 and 25,000 in the year 2004.

Based on the above information, answer the following two questions:
(A) What was the population of the Swastik’s village in the year 2009? (2)
(B) What will be the population of the village after 15 years from the year 1999? (2)
Answer:
Let the temperature of the body be T°C.
Then, according to the question, dT ,
\(\frac{d T}{d t}\) = k(T – 25)
⇒ \(\frac{d T}{\mathrm{~T}-25}\) = k dt
Integrating both sides, we get
log (T – 25) = kt + log C
⇒ log \(\frac{C}{\mathrm{~T}-25}\) = kt
or T – 25 = Ce^kt ………….. (i)
when t = 0, T = 100
Putting these values in (i), we get
100 – 25 = Ce⁰
⇒ C = 75
∴ T – 25 = 75e^kt …………….. (ii)
When t = 1, T = 75
Thus, from (ii), we get
T – 25 = \(\left(\frac{2}{3}\right)^{2}\)
or T = 25 + 75\(\left(\frac{2}{3}\right)^{t}\) ……… (iii)

(A) Putting t = 3, in eq. (iii), we get
T = 25 + 75\(\left(\frac{2}{3}\right)^{3}\)
= 25 + 75 × \(\frac{8}{27}\)
= 47.22°C

(B) Putting T = 58°C, in eq. (iii), we get
58 = 25 + 75\(\left(\frac{2}{3}\right)^{t}\)
⇒ \(\left(\frac{2}{3}\right)^{t}=\frac{33}{75}\)
or \(\left(\frac{2}{3}\right)^{t}=\frac{11}{25}\)
⇒ t = 2 minutes
OR
Let y be the populations of the Swastik’s village at any time t.
Then, according to the question, dy
\(\frac{d y}{d t}\)
where, k is an arbitrary constant.
⇒ \(\frac{d y}{y}\) = kdt
Integrating both sides, we get
log y = kt + C …(i)
Let the year 1999 be the initial year.
So, at t = 0, y = 20,000
putting these values in (i), we get
log 20000 = k(0) + C
⇒ C = log 20,000
∴ (i) becomes
log y = kt + log 20,000 …(ii)
So, in 2004, t = 5 and y = 25,000.
Putting these values in (ii), we get
log 25,000 = 5k + log 20,000
⇒ k = \(\frac{1}{5}\)log\(\left(\frac{5}{4}\right)\)
Hence, by (ii), we have