CBSE Sample Papers for Class 12 Physics Term 2 Set 1 with Solutions

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 1 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 1 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B, and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A consists 3 questions of 2 marks each.)

Question 1.
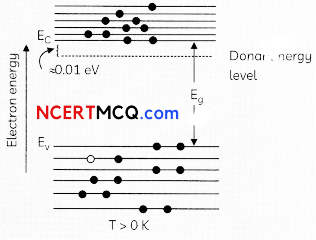
In a pure semiconductor crystal of Si, if antimony is added then what type of extrinsic semiconductor is obtained. Draw the energy band diagram of this extrinsic semiconductor so formed. (2)
Answer:
As given in the statement antimony is added to pure Si crystal, then an n-type extrinsic semiconductor would be so obtained Since antimony (Sb) is a pentavalent impurity. Energy level diagram of n-type semiconductor

Related Theory
Each pentavalent impurity atom donates one extra electron: it is known as donor. Most of the current is carried by negatively charged electrons, so, the semiconductors doped with donor type impurities are known as n-type semiconductors.

Question 2.
Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but same orbital angular momentum according to the Bohr model? Justify your answer.
OR
Explain how does (A) photoelectric current and (B) kinetic energy of the photoelectrons emitted in a photocell vary if the frequency of incident radiation is doubled, but keeping the intensity same? Show the graphical variation in the above two cases. (2)
Answer:
No
Because according to Bohr’s model,
E_n = \(-\frac{13.6}{n^{2}}\) and electrons having different energies belong to different levels having different values of n.
So, their angular momenta will be different, as ‘
L = mvr = \(\frac{n h}{2 \pi}\)
OR
(A) The increase in the frequency of incident radiation has no effect on photoelectric current. This is because of incident photon of increased energy cannot eject more than one electron from the metal surface. f = photoelectric current f = frequency of incident radiation fo = threshold frequency

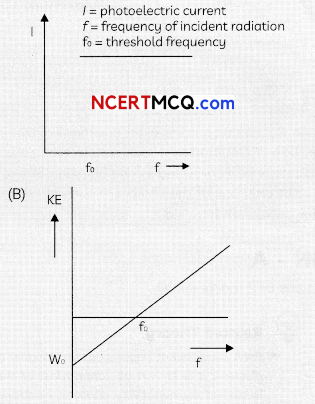
The kinetic energy of the photoelectron becomes more than the double of its original energy. As the work function of the metal is fixed, so incident photon of higher frequency and hence higher energy will impart more energy to the photo electrons.

Question 3.
Name the device which converts the change in intensity of illumination to change in electric current flowing through it. Plot l-V characteristics of this device for different intensities. State any two applications of this device.(2)
Answer:
Photodiodes are used to detect optical signals of different intensities by changing current flowing through them.

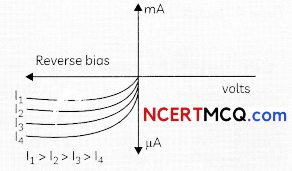
I-V Characteristics of a photodiode Applications of photodiodes:
1. In detection of optical signals.
2. In demodulation of optical signals.
3. In light operated switches.
4. In speed reading of computer punched cards.
5. In electronic counters
(any two out of these or any other relevant application)

SECTION – B
(Section B consists 8 questions of 3 marks each.)

Question 4.
Derive an expression for the frequency of radiation emitted when a hydrogen atom de-excites from LeveL n to Level (n – 1). Also show that for Large values of n, this frequency equals to classical frequency of revolution of an eLectron. (3)
Answer:
From Bohr’s theory, the frequency f of the radiation emitted when an electron de – excites from Level n₂ to Level, n₁ is given as,
f = \(\frac{2 \pi^{2} m k^{2} z^{2} e^{4}}{h^{3}}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)
Given n₁ = n – 1 = n . derivation of it
f = \(\frac{2 \pi^{2} m k^{2} z^{2} e^{4}}{h^{3}} \frac{(2 n-1)}{(n-1)^{2} n^{2}}\)
For large n. 2n- 1 = 2n,n- 1 =n and z= 1
Thus, f = \(\frac{4 \pi^{2} m k^{2} e^{4}}{n^{3} h^{3}}\)
which is same as orbital. frequency of etectron in nth orbit.
f = \(\frac{v}{2 \pi r}=\frac{4 \pi^{2} m k^{2} e^{4}}{n^{3} h^{3}}\)

Question 5.
Explain with a proper diagram how an ac signal can be converted into dc ( pulsating) signal with output frequency as double than the input frequency using pnjunction diode. Give its input and output waveforms. (3)
Answer:
A junction diode aLlows current to pass only when it is forward biased. So, Wan alternating voltage is applied across a diode the current flows only in that part of the cycle when the diode is forward biased. This property is used to rectiy alternating voltages and the circuit used for this purpose is called a rectifier.

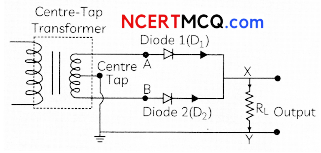
Explanation: A full wave rectifier converts ac signal into dc signaL During positive half of the cycle, diode 1 is forward biased and diode 2 is reverse biased. During negative half of the cycle, diode 1 is forward biased. Output voltage is obtained during both half cycles. This process is known as rectification.

Caution:
Output frequency double of input frequency is not possible in half wave rectifier. In half wove rectifier, there will be no output voltage, hence, diode will conduct during positive half cycle only.

Question 6.
How Long can an electric Lamp of 100 W be kept glowing by fusion of 2 kg of deuterium? Take the fusion reaction as ₁¹H+₁²H → ₂³He+n +3.27 MeV (3)
Answer:
Number of atoms present in 2 g of deuterium = 6 x10²³
Number of atoms present in 20 Kg of deuterium = 6 x 10²⁶
Energy released in fusion of 2 deuterium atoms = 3.27 MeV
Energy reLeased in fusion of 2.0 Kg of deuterium atoms

= \( \frac{3.27}{2}\) x 6 x 1026 MeV
= 9.81 x. 10²⁶ MeV
= 15.696 x 10¹³J
Energy consumed by bulb per sec = 100 J
Time for which bulb will glow
= \(\frac{15.696 \times 10^{13}}{100}\)
s = 4.97 x 10⁴ year

Question 7.
Define wavefront. Draw the shape of refracted wavefront when the plane incident wave undergoes refraction from optically denser medium to rarer medium. Hence prove Snell’s law of refraction. 3
Answer:
A locus of points, which oscillate in phase is called a wavefront. A wavefront is defined as a surface of constant phase.

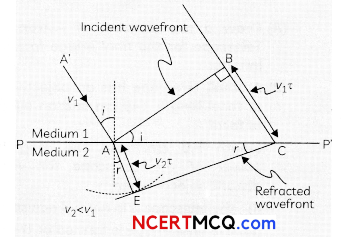
Explanation: A wavefront is defined as the continuous locus of aLL such particles of the
medium which are vibrating in the same phase at any instant.

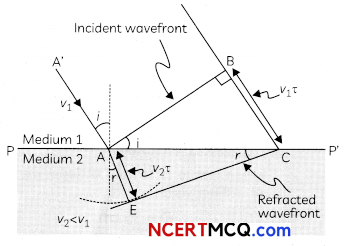
sin∠BAC=sini= \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
From the right ΔAEC
sin ∠ECA =sin r = \(\frac{\mathrm{AE}}{\mathrm{AC}}\)
\(\frac{\sin i}{\sin r}=\frac{\mathrm{BC}}{\mathrm{AE}}=\frac{v_{1} \tau}{v_{2} \tau}\)
This is the Snells tow of refraction.

Question 8.
(A) Draw a ray diagram of compound microscope for the final image formed at least distance of distinct vision?
(B) An angular magnification of 30X is desired using an objective of focal length 1.25 cm and an eye piece of focal length 5 cm. How will you set up the compound microscope for the finaln image formed at least distance of distinct vision?
OR
(A) Draw a ray diagram of Astronomical Telescope for the final image formed at infinity.
(B) A small telescope has an objective lens of focal length 140 cm and an eyepiece of focal length 5.0 cm. Find the magnifying power of the telescope for viewing distant objects when
(i) the telescope is in normal adjustment,
(ii) the final image is formed at the least distance of distinct vision. (3)
Answer:
(A) Diagram of Compound Microscope for the final image formed at D:

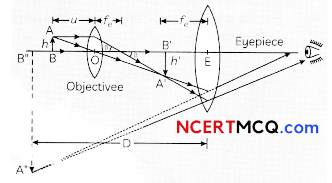
(B) m₀ = 30, i₀ = 1.25 cm, f_e = 5 cm
when image is formed at least distance of aistinct vision,
D = 25 cm
Angular magnification of eyepiece
m_e = \(\left(1+\frac{D}{f_{e}}\right)=1+\frac{25}{5} \) = 6

Total Angular magnification, m = m₀m_e ⇒
m₀ = \(\frac{m}{m_{e}}=\frac{30}{6}\) = 5
As the objective lens forms the real image,
m₀= \(\frac{v_{0}}{u_{0}}\) – 5 ⇒ v₀ = -5u₀
using Lens equation, u_e = \(\frac{25}{6}\)

Thus, object is to be placed at 1.5 cm from the objective and separation between the two lenses should be
L = v₀ + |U_e| = 11.67 cm
OR
(A) Ray diagram of astronomical telescope when image is formed at infinity.

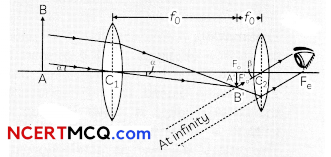
(B) (i) In normal adjustment: Magnifying power.
m=f₀/f_e=(140/5)= 28
(ii) When the final image is formed at the east distance of distinct vision (25 cm):
m = \(\frac{f_{o}}{f_{e}}\left(1+\frac{f_{e}}{D}\right)(28 \times 1.2)\) = 33.6

Question 9.
Light of waveLength 2000 Å falls on a metal surface of work function 4.2 eV.
(A) What is the kinetic energy (in eV) of the fastest electrons emitted from the surface?
(B) What will be the change in the energy of the emitted eLectrons if the intensity of Light with same waveLength is doubled?
(C) If the same Light faits on another surface of work function 6.5 eV, what will be the energy of emitted electrons? (3)
Answer:
λ = 2000 Å = (2000 x 10^-10)m
W₀ = 4.2 eV
h = 6.63 x 10^-34 Js

(A) Using Einstein’s photoelectric equation
K. E. = (6.2 – 4.2) eV = 2.0 eV

(B) The energy of the emitted electrons does not depend upon intensity of incident Light; hence the energy remains unchanged.

(C) For this surface, electrons will not be emitted as the energy of incident light (6.2 eV) is less than the work function (6.5 eV) of the surface.

Question 10.
The focal length of a convex lens made of glass of refractive index (1.5) is 20 cm. What will be its new focal length when placed in a medium of refractive index 1.25 ? Is focal length positive or negative? What does it signify? (3)
Answer:
Given a_μg = 1.5
Focal length of the given convex lens when it is placed in air is
f= + 20 cm
Refractive index of the given medium with respect to air is
a_μm = 1-25
New focal length of the given convex lens when placed in a medium is f’

New focal length is positive.
The significance of the positive sign of the focal length is that given convex lens is still converging in the given medium.

Question 11.
(A) Name the e.m. waves which are suitable for radar systems used In aircraft navigation. Write the range of frequency of these waves.
(B) If the Earth did not have atmosphere, would its average surface temperature be higher or lower than what it is now? Explain.
(C) An e.m. wave exerts pressure on the surface on which it is incident. Justify.
OR
(A) If the slits in Young’s double-slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit”. Justify the above statement through a relevant mathematical expression.
(B) Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit. 3
Answer:
(A) Microwaves are suitable for the radar system used in aircraft navigation. Range of frequency of microwaves is 108 Hz to 1011 Hz.

(B) If the Earth did not have atmosphere, then there would be absence of greenhouse effect of the atmosphere. Due to this reason, the temperature of the earth would be lower than what it is now.

(C) An e.m. wave exerts pressure on the surface on which it is incident. Justify An e.m. wave carries a linear momentum with it and the linear momentum carried by a portion of wave having energy U, which is given by p = U/c, where U = potential energy and c = speed of light.
Thus, if the wave incident on a material surface is completely absorbed, it delivers potential energy U and momentum p = Uc to the surface.
If the wave is totally reflected, the momentum delivered is p = 2U/c because the momentum of the wave changes from p to -p.
Therefore, it follows that an e.m. waves incident on a surface exert a force and hence a pressure on the surface.
OR
(A) The total intensity at o point where the phase difference is Φ. is given by I = I₁ + I₂ + 2\( \sqrt{1_{1} I_{2}}\) Φ
Here I₁ and I₂ are the intensities of two individual sources which are equal.
When Φ is 0,I = 4I₁
When Φ is 90°, I = 0
Thus intensity on the screen varies between 4I₂ and 0.
(B) Intensity distribution as function of phase angle, when diffraction of light takes place through coherently illuminated single slit

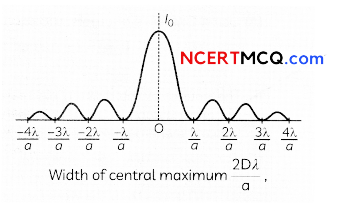
SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
CASE STUDY: MIRAGE IN DESERTS

To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object.
Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage.
This type of mirage is especially common in hot deserts. Based on the above facts, answer the following questions:
(A) Which of the following phenomena is prominently involved in the formation of mirage in deserts?
(i) Refraction, Total internal Reflection
(ii) Dispersion and Refraction
(iii) Dispersion and scattering of light
(iv) Total internal Reflection and diffraction.

(B) A diver at a depth 12 m inside water
\(\left(a_{\mu \omega}=\frac{4}{3}\right)\) sees the sky in a cone of semi-vertical angle

• sin^-1\(\frac{4}{3}\)
• tan^-1 \(\frac{4}{3}\)
• sin^-1 \(\frac{4}{3}\)
• 90°

(C) In an optical fibre, if n₁ and n₂ are the refractive indices of the core and cladding, then which among the following, would be a correct equation?
(i) n₁ < n₂
(ii) n₁ = n₂
(iii) n₁ < n₂
(iv) n₁ > n₂

(D) A diamond is immersed in such a liquid which has its refractive index with respect to air as greater than the refractive index of water with respect to air. Then the critical angle of diamond- liquid interface as compared to critical angle of diamond -water interface will:
(i) depend on the nature of the liquid only
(ii) decrease
(iii) remain the same
(iv) increase.

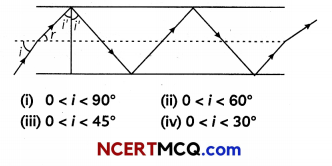
(E) The following figure shows a cross-section of a ‘light pipe’ made of a glass fiber of refractive index 1.68.
The outer covering of the pipe is made of a material of refractive index 1.44.
What is the range of the angles of the incident rays with the axis of the pipe for the following phenomena to occur. (5)

Answer:
(A)
(i) Refraction, Total internal reflection
Explanation: When Light passes from cold air to hot air, tight tends to bend from its path which is known as refraction. As the tight is refracted, it reaches to o point where it forms a 90° angle. Hence refraction and total internal reflection are involved in formation of mirages.

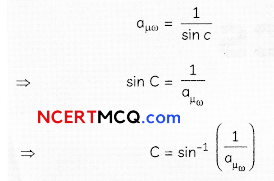
(B) (iii) sin^-1 \(\left(\frac{3}{4}\right)\)

(C) (iv) n₁ > n₂
The refractive index of the core should be greater than the refractive index of the dadding.

(D) (iv) increase
\(\mathrm{I}_{\mu d}=\frac{1}{\sin c}=\frac{\mu_{d}}{\mu_{1}}\)
μ₁ = μ_ω
Thus C>C’

(E) (ii) 0<i<60°, ^lμ₂ = \(\frac{1}{\sin C^{\prime}}\)
SinC’= \(\frac{1.44}{1.68}\) = 0.8571
⇒ C = 59°
Total, internat reflection wilL occur if the angle i > i’c,
i.e., if i’> 59° or when r < r_max where r_max = 90° – 59°= 31°.
Using Snell’s Law.

\(\frac{\sin i_{\max }}{\sin r_{\max }}\) = 1.68
sin i_max = 1.68 x sin r_max
= 1.68 x sin 31° = 1.68 x 0.5 150 = 0.8662
Thus all incident rays which make angles in the range 0 < i < 60° with the axis of the pipe wilt suffer total internal reftections in the pipe.