CBSE Sample Papers for Class 12 Physics Term 2 Set 3 with Solutions

Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 3 with Solutions

Time Allowed: 2 Hours
Maximum Marks: 40

General Instructions:

• There are 12 questions in all. All questions are compulsory.
• This question paper has three sections: Section A, Section B, and Section C.
• Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
• There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
• You may use log tables if necessary but use of calculator is not allowed.

SECTION – A
(Section A contains 3 questions of 2 marks each.)

Question 1.
Under what conditions does the phenomenon of total internal reflection take place? Draw a ray diagram showing how a rag of light deviates by 90° after passing through a right-angled isosceles prism.
OR
What are the (A) momentum, (B) de Broglie wavelength of an electron with kinetic energy of 120 eV? (2)
Answer:
The phenomenon of total internal reflection occurs when,
(A) Angle of incidence is equaL or greater than critical angle that is i ≥ C
(B) Angle of incidence is equal or greater than critical angle that is i ≥ C In case of right-angle isosceles triangle, if light rays fall normally on face AB the light ray incident of face AC with angle of incidence greater than the critical angle.

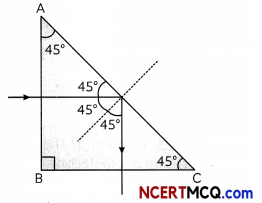
Hence, total Internat reflection will occur with normal to the surface of BC. The phenomenon in which a ray of light travelling at an angle of incidence greater than the critical angle from denser to a rarer medium is totally reflected back into the denser medium is called total internal reflection.
OR
Here, kinetic energy of electron
E = 120 eV
= 120 x 1.6 x 10^-19 J
= 192 x 10^-19J

(A) Momentum of electron,
P = \(\sqrt{2 m_{e} \mathrm{E}} \)
= \(\sqrt{2 \times 9.1 \times 10^{-31} \mathrm{~kg} \times 192 \times 10^{-19} \mathrm{~J}}\)
= 5.9 x 10^-24 Kg ms^-1

(B) de – Brogue wavelength,
P = \(\frac{h}{\lambda}\)
λ = \(\frac{h}{p}\)
= \(\frac{6.63 \times 10^{34} \mathrm{Js}}{5.9 \times 10^{-24} \mathrm{~kg} \mathrm{~ms}^{-1}}\)
= 1.12 x 10^-10
λ = 1.12 Å.

Question 2.
From the relation R = R_o A^1/3 where R_o is a constant and A is the mass number of a nucleus, show that the nuclear matter density is independent of A? (2)
Answer:
If m is the overage mass of a nucleon and R is the nucLear radius, then mass of nucteus = mA,
where A is the mass number of the element Volume of the nucleus
V = \(\frac{4}{3} \pi R^{3}\)
Given R = R₀ A^1/3
⇒ V= \(\frac{4}{3} \pi\left(R_{0} A^{1 / 3}\right)^{3}\)
⇒ V = \(\frac{4}{3} \pi R_{0}^{3} A\)

Density of nuclear matter,
ρ = \(\frac{m \mathrm{~A}}{\mathrm{~V}}\)
⇒ ρ = \(\frac{m \mathrm{~A}}{\frac{4}{3} \pi \mathrm{R}_{0}^{3} \mathrm{~A}}\)
ρ = \(\frac{3 m}{4 \pi R_{0}^{3}}\)
This shows that nuclear density is independent of A.

Question 3.
The given graph shows the V-I characteristics of a semiconductor diode.

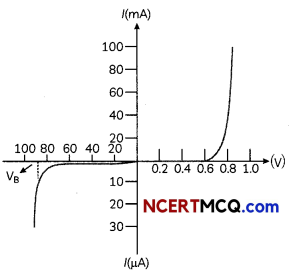
(A) Identify the semiconductor diode used.
(B) Draw the circuit diagram to obtain the given characteristics of this device.(2)
Answer:
(A) Since the voltages quoted in the given diagram are much more than actual values and It is usually < 0.6 V. The semiconductor the diode used is Zener diode.
(B) The circuit diagram for the characteristics of Zener diode is shown as: For forward bias Zener diode

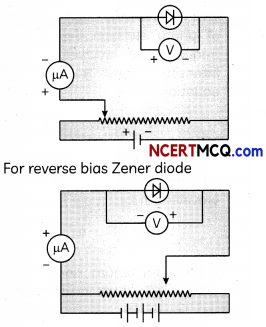
SECTION – B
(Section B consists of 8 questions of 3 marks each.)

Question 4.
Write Einstein’s photoelectric equation and mention which important features in photoelectric effect can be explained with the help of this equation. The maximum kinetic energy of the photo-electrons gets doubled when the wavelength of light incident on the surface changes from λ₁ to λ₂. Derive the expressions for the threshold wavelength λ₀ and work function for the metal surface. (3)
Answer:
Einstein’s photoelectric equation is given by
hv =Φ₀ + K_max
where K_max = Maximum kinetic energy of the photoelectron
v = Frequency of the Light radiation
h = Planck’s constant
Φ₀= Work function

We have.
K_max = \(\frac{1}{2} m v^{2}_{\max }\)
where, v_max = Maximum velocity of the emitted photoelectron
m = Mass of the photoelectron
Therefore.
hv =Φ₀= \(\frac{1}{2} m v^{2}_{\max }\)
If v₀ is the thresho[d frequencj, then the work function can be written as
Φ₀ = hv

Hence,
hv = hv₀ + \(\frac{1}{2} m v^{2}_{\max }\)
hv – hv₀ = \(\frac{1}{2} m v^{2}_{\max }\)
\(\frac{1}{2} m v^{2}\) = h (v -v₀)

The above equations explains the following results:
(i) If v < v₀, then the maximum kinetic energy is negative, which is impossible.
Hence, photoelectric emission does not take place for the incident radiation below the threshold frequency. Thus, the photoelectric emission can take place if v > v₀.

(ii) The maximum kinetic energy of emitted photoelectrons is directly proportional to the frequency of the incident radiation. This means that maximum kinetic energy of photoelectrons depends only on the frequency of incident light not on the intensity According to the photoelectric equation.
K₁ = \(\frac{1}{2}\) mv²
= hv – Φ₀
Let the maximum kinetic energy for the wavelength λ₂
K₁ = \(\frac{h c}{\lambda_{1}}-\phi_{0}\) ……………………… (i)
Let the maximum kinetic energy for the waveLength of the incident λ₂ be K₂
K₂ = \(\frac{h c}{\lambda_{2}}\) – Φ₀ …………………. (ii)
(Kmax)2 = (Kmax)1 (given)

Work function is the energy required to eject o photoeLectron from the metal.
Φ₀ = \(\frac{h c}{\lambda_{0}} [latex]
∴ Φ₀ = [latex]\frac{h c\left(2 \lambda_{2}-\lambda_{1}\right)}{\lambda_{1} \lambda_{2}}\).

Question 5.
Draw a ray diagram showing the image formation by a compound microscope. Hence obtain expression for total magnification when the image is formed at infinity. (3)
Answer:
A compound microscope consists of two convex parallel Lenses separated by some distance. The Lens nearer to the object is called the objective lens. The lens through which the final image is viewed is called the eyepiece or eye lens.

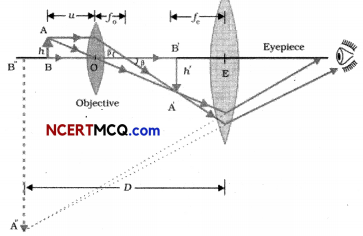
The magnification produced by the compound microscope is the product of the magnifications produced by the eyepiece and objective.
M = M_e X M₀

Where M_e and M₀ are the magnifying powers of the eyepiece and objective respectively. If u₀ is the distance of the object from the objective and v₀ is the distance of the image from the objective, then the magnifying power of the objective is:
M₀ = \(\frac{h^{\prime}}{h}=\frac{L}{f_{0}}\)

Where, h, h’ are object and image heights respectively and f₀ is the focal length of the objective and L is the tube length Le., the distance between the second focal point of the objective and the first focal point of the eyepiece.
When the final image is at infinity,
M_e = \(\frac{D}{f_{e}}\)
Magnifying power of compound microscope.
M = M₀ x M_e
= \(\frac{L}{f_{0}} \times \frac{D}{f_{e}}\)

Question 6.
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young’s double-slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
OR
In a Geiger Marsden experiment, calculate the distance of closest approach to the nucleus of Z = 75, when an a-particle of 5 MeV energy impinges on it before it comes momentarily to rest and reverse its direction.
How will the distance of closest approach be affected when the kinetic energy of the a particle is doubled? (3)
Answer:
Given:
λ₁ = 800 nm
=800x 10^-9m
= 600 nm
λ₂ =600 x 10^-9m
D=14m
d = 0.28 mm
= 0.28 x 10^-3m
Suppose n₁th, maximum corresponds to wavelength λ₁ and it coincides with n₂th maximum corresponding to wavelength λ₂.
∴ \(n_{1} \frac{\lambda_{1} D}{d}=n_{2} \frac{\lambda_{2} D}{d}\)
Thus, 3^rd maximum corresponding to wavelength 800 nm coincides with 4^th maximum corresponding to wavelength 600
nm.
And the minimum distance is given by,
X_min = n₁\(\frac{\lambda_{1} D}{d}\)
= \(\frac{3 \times 800 \times 10^{-9} \times 1.4}{0.28 \times 10^{-3}}\)
X_min = 12 mm
OR
Let r₀ be the centre to centre distance between the α-particle and nucleus when the α-particle is at its stopping point.
Now, E_k = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(2 e)(Z e)}{r_{0}}\)
r₀ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(2 e)(Z e)}{E_{K}}\)
Given, E_k = 5 x 10⁶ eV
= 5 x 10⁶ x 1.6 x 10^-19 V
Z = 75
r₀ = \(\frac{9 \times 10^{9} \times 75 \times 2 \times\left(1.6 \times 10^{-19}\right)^{2}}{5 \times 10^{6} \times 1.6 \times 10^{-19}}\)
= \(\frac{3456 \times 10^{9} \times 10^{-38}}{8 \times 10^{-13}}\)
= 432 x 10^-16 m
= 43.2 x 10^-15 m
= 43.2 fm
Since, distance of cLosest approach (r₀) is given
r₀ =\(\frac{1}{4 \pi \varepsilon_{0}} \frac{(2 e)(Z e)}{E_{K}}\)
⇒ r₀ ∝ \(\frac{1}{E_{K}}\)
So, when kinetic energy of α-particle is doubled the distance between closest approach r₀ is halved.

Related Theory:
kinetic energy of’ α-particle is inverseLy proportional the distance of closest approach.

Question 7.
(A) What type of wavefront will emerge from a point source and a distant light source?
(B) Make a labelled diagram showing the wavefronts in reflection from:
(i) Plane mirror
(ii) Curved mirror (3)
Answer:
(A) From o point source, the wavefront is diverging spherical wavefront and from a distant Light source, the wavefront is plane front.
(B) (i) Reflection from plane mirror:

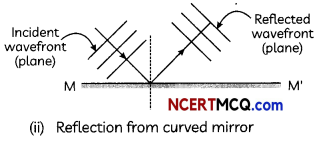
(ii) Reflection from curved mirror

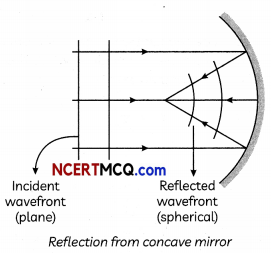
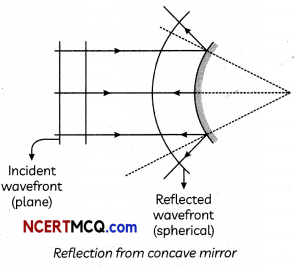
Question 8.
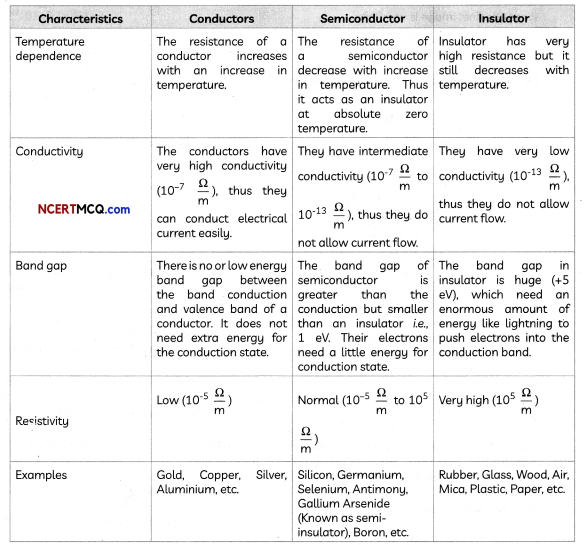
Distinguish on the basis of features between conductors, insulators and semiconductors. (3)
Answer:

Question 9.
Describe the role of processes involved in the formation of p-n junction with the help of a diagram. (3)
Answer:
Two process occur during the formation of p-n junction are diffusion and drift.
(i) Diffusion: In n-type semiconductors, the concentration of electrons is much greater as compared to concentration of holes arid in p-type semiconductors, the concentration of holes is much greater than concentration of electrons. When p-n junction is formed, concentration gradient is set up. The holes diffuse n-side and electrons dislikes the top-side. This motion of charge carriers gives rise to diffusion current across the junction.

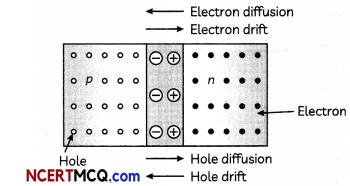
(ii) Drift: The drift charge carriers occur due to the electric field. As potential barrier is built, on electric field is directed from n-side to p-side of the junction. This field causes motion of electrons on p-side of the junction to n-side of the junction and motion of holes on n-side to p-side of the junction. This is known as drift current which is opposite direction of diffusion current

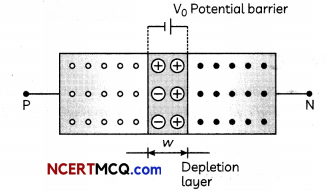
Question 10.
(A) Can a charge moving with a constant velocity act as a source of electromagnetic waves?
(B) In a plane EM wave, the electric field oscillates sinusoidally at a frequency of 2 x 10¹⁰Hz and amplitude 48 vm’1.
(i) What is the wavelength of the wave?
(ii) What is the amplitude of the oscillating magnetic field? (3)
Answer:
(A) A charge moving with a constant velocity has zero acceleration and according to the classical theory of electromagnetism only accelerated charge can produce electromagnetic wave. Therefore, a charge moving with a constant velocity cannot produce electromagnetic wave. Frequency of the electromagnetic wave,
v=2.0x 1010Hz
Electric field amplitude, E₀ = 48 Vm-1
Speed of light, c = 3 x 108 m/s
E₀ = 48 \(\frac{\mathrm{V}}{m}\)
and c=3 x 10⁸ms^-1
(i) λ = \(\frac{c}{v}\)
= \(\frac{3 \times 10^{8} \mathrm{~ms}^{-1}}{2 \times 10^{10} \mathrm{~Hz}}\)
= 1.5 x 10^-2 m
(ii) c = \(\frac{E_{0}}{B_{0}}\)
B₀ = \(\frac{E_{0}}{c}\)
= \(\frac{48 \frac{\mathrm{V}}{m}}{3 \times 10^{8} \mathrm{~ms}^{-1}}\)
= 1.6 x 10^-7 T

Question 11.
Give reason for following observations in YDSE.
(A) The resultant intensity at any point on the screen varies between 0 and 4 times the intensity, due to one slit.
(B) A few coloured fringes, around a central white region, are observed on the screen, find the source of monochromatic light is replaced by white light.
(C) Why no interference is seen when two coherent sources are infinitely close to each other or when they are far apart from each other?
OR
Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (BE/A) versus the mass number A.(3)
Answer:
(A) The resuLtant intensity, at any point on the screen is given by.
I = 4I₀, cos²\(\frac{\phi_{0}}{2}\)
For constructive interference;
Φ₀= O, 2π. 4π and so on
I = O for minimum intensity
For destructive interference:
Φ₀ = π, 3π, 5π and so on
I = 4I₀ for maximum intensity.
Therefore, intensity varies from zero to four times the intensity due to single slit.

(B) The interference patterns due to different colours of white light overtop incoherently.
The central bright fringes for different colours are at the same position. Therefore the central fringe is white and the fringes closest, on either side of central white fringe, are red and farthest wilt appear blue. After a few fringes, no clear fringe pattern is seen.

(C) When two coherent sources are placed infinitely close to each other, the fringe width becomes very large. Even a single fringe width may occupy the entire screen. When the sources are far apart, the fringe width increases. At a very large separation. it becomes too small to be detected. Hence, the interference pattern cannot be detected when the sources are infinitely close to each other or kept far apart from each other.
OR
A plot of binding energy per nucleon moss number is shown in the figure given below

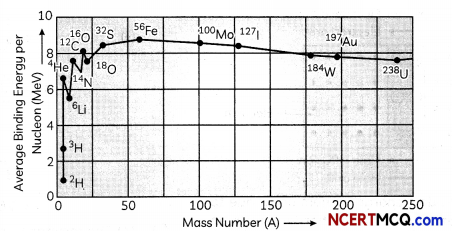
(A) When we move from the heavy nuclei region to the middle region of the plot, we find that there will be again in the overall binding energy and hence results in release of energy. This indicates that energy can be released when a heavy nucleus (A ~ 240) breaks into two roughly equal fragments.
This process is called nuclear fission.

(B) Similarly. when we move from lighter nuclei to heavier nuclei, we again find that there will be again in the overall binding energy and hence release of energy takes place. This indicates that energy can be released when two or more Lighter nuclei fuse together to form a heavy nucleus. This process is called nuclear fusion.

SECTION – C
(Section C consists one case study-based question of 5 marks.)

Question 12.
Dispersion is the splitting of white light into its constituent colours. The dispersion occurs in prisms but not in glass slabs because of its geometric design. In a slab, the opposite sides are parallel to each other whereas in case of the prism, the sides are not parallel to each other.

In prism, the dispersion occurring at one face and is enhanced at the other end but in glass slabs, dispersion occurring at one end is neutralized by refraction at the other end. When we put two prisms in series but in opposite direction, they will act as a glass slab together.

Based on the above facts, answer the following questions:
(A) Two parallel rays of red and violet colour pass through a glass stab as shown In the figure. Which of the following is correct?

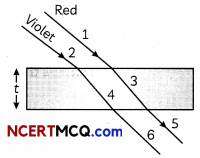
(i) 3 and 4 are parallel
(ii) 4 and 5 are parallel
(iii) 6 and 3 are parallel
(iv) 2 and 5 are parallel.
(B) A convex lens is made up of two types of material Upper half is made by the refractive index n₁ and Lower half is made by the refractive index n₂. Which of the following is true for rays coming from infinity?
(ï) Two images are formed
(ii) One image is formed
(iii) Continuous ¡mage is formed between the focal points of upper and tower tens.
(iv) Image is not formed

(C) Maximum Lateral displacement of ray Light incident on a stab of thickness t is:
(i) \(\frac{t}{2}\)
(ii) \(\frac{t}{3}\)
(iii) \(\frac{t}{4}\) (iv) t
(D) The refractive index of water, glass, and diamond are 1.33, 1.50, and 2.40, respectively. What is the refractive index of the diamond relative to water and of glass relative to diamond, respectively are nearly?
(i) 1.80, 1.6
(ii) 0.5 54, 1.6
(iii) 1.80, 0.625
(iv) 0.554, 0.625

(E) An air bubble in a glass slab with refractive index 1.5 (near-normal incidence) is 5 cm deep when viewed
from one surface and 3 cm deep when viewed from the opposite face. The thickness (in cm) of the slab is:
(i) 8
(ii) 10
(iii) 12
(iv) 16 (5)
Answer:
(A) (d) 2 and 5 are parallel Explanation: When refraction occurs through a parallel glass slab, the emergent ray is parallel to incident ray. From the given diagram
6||2,5||1
Because 1 || 2
⇒ 2 || 5
(B) (a) Two images are formed
Explanation: The given lens is made of two materials of different refractive indices, so it has two focal lengths. Hence, two images are formed.

‘Related Theory
Due to the two materials of different refractive indices lens will form two images (C) (d)t
Explanation: For I = 90⁰ and r=0⁰, Lateral shift is maximum.
Lateral shift for a sLob of t thickness
LS = t x sin\(\frac{(i-r)}{\cos r}\)
LS = t
Hence, the Lateral shift is equaL to thickness t.

Caution:
Students are often confused about the values of i and r when lateral shift is maximum. in this case i = 90° and r= 0°
(D) (c) 1.80, 0.625
Explanation: n_w = 1.33,
n_g = 1.5
and n_d= 2.4
Now, _wn_d = \(\frac{n_{d}}{n_{w}}\)
= \(\frac{2.4}{1.33}\) = 1.80
Further, _dn_g = \(\frac{n_{g}}{n_{d}}\)
= \(\frac{1.50}{2.4}\) = 0.625

(E) (c)12
Explanation: Refractive index
n= \(\frac{\text { Real thickness }}{\text { Apparent”thickness }}\)
ReaL thickness = n x Apparent thickness
= 1.5 x (5 + 3) = 12 cm