Students can access the CBSE Sample Papers for Class 12 Physics with Solutions and marking scheme Term 2 Set 4 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 12 Physics Standard Term 2 Set 4 with Solutions
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- There are 12 questions in all. All questions are compulsory.
- This question paper has three sections: Section A, Section B, and Section C.
- Section A contains three questions of two marks each, Section B contains eight questions of three marks each, Section C contains one case study-based question of five marks.
- There is no overall choice. However, an internal choice has been provided in one question of two marks and two questions of three marks. You have to attempt only one of the chokes in such questions.
- You may use log tables if necessary but use of calculator is not allowed.
SECTION – A
(Section A contains 3 questions of 2 marks each.)
Question 1.
What is an ideal diode and draw the output waveform across R for the input waveform given below? (2)
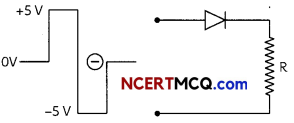
Answer:
The diode offering zero resistance in forward bias, infinite resistance in reverse bias and having no potential barrier ideal diode. In the first half cycle the diode is forward biased and conducts, shown output is obtained across r, while in the next half-cycle the diode is reverse biased does not conduct, so no output is obtained across R.

Question 2.
In the given fusion reaction, find the mass defect, Q-value and state whether the fusion is energetically favorable? He4+He4 → Be8
m (Be8) = 8.0053 u and m(He4) = 4.0026 u.
OR
In Young’s double-slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What type of information can we obtain from slope of the curve? (2)
Answer:
He4, He4 →, Be8 + Q
Δm=2 x 4.0026-8.0053 = 8.0052-8.0053
=-0.0001
Q=(2mHe — mHe)c = (2 x 4.0026 – 8.0053) x 931.5 MeV = – 931.5 KeV
Since Q is negative, the fusion is not energetically favorable.
OR
The fringe width in Young’s double-slit experiment is given by
β = \(\frac{\lambda D}{d}\)
D = distance between slit and screen
d = distance between slits
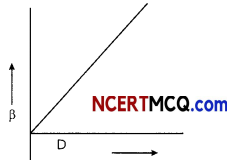
So, β ∝ D
It is linear graph with slope \(\frac{\lambda}{d}\) . So the fringe width to vary Linearly with distance of screen from the slits, the ratio of wavelength to distance between the slits should remain constant. Therefore, it is advised to take wavelengths incident light nearly equal to the width of the slit.
Related Theory:
In Youngs double-slit experiment fringe width is directly proportional to the distance of screen the slit.
![]()
Question 3.
Describe a reflecting type telescope and mention its advantages. (2)
Answer:
Cassegrain telescope is a reflecting type telescope.
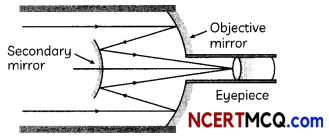
Telescopes with mirror objectives are called reflecting telescopes. Advantages of taking mirror objectives are:
(A) There is no chromatic aberration in mirrors.
(B) MechanicaL support is much less of a problem since Lens weighs more than mirror of equal. equivalent optical quality.
(C) If a parabolic reflecting surface is chooser, spherical aberration is also removed.
Related Theory
The Largest reflecting telescope in the world ore the pair of rack telescopes in Hawai USA. with reflectors
of 10 meters in diameter.
SECTION – B
(Section B consists of 8 questions of 3 marks each.)
Question 4.
An electron and a photon each have a wavelength of 1.50 nm. Find:
(A) their momentum.
(B) the energy of the photon.
(C) the kinetic energy of the eLectron. (3)
Answer:
(A) For each electron or photon, momentum,
p = \(\frac{h}{\lambda} \)
= \(\frac{6.63 \times 10^{-34}}{1.5 \times 10^{-9}}\)
= 4.42 x 10-25kg\(\frac{m}{\text { sec }}\)
(B) E = \(\frac{h c}{\lambda}\)
= \(\frac{\left.\left.6.63 \times 10^{-34}\right) 3 \times 10^{8}\right) e V}{\left(1.5 \times 10^{-9}\right)\left(1.6 \times 10^{-19}\right)}\)
= 828.75 eV
(C) Ek = \(\frac{1}{2} \frac{p^{2}}{m}\)
= \(\frac{1\left(4.42 \times 10^{-25}\right)^{2}}{2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19}}\)eV
= 0.671 eV
Question 5.
(A) Prove the behavior of a plane wavefront by using Huygens’s geometrical construction when:
(i) passing through o biconvex lens and
(ii) reflecting by a concave mirror.
(B) ExpLain why the refracted Light have the same frequency as that of the incident Light when monochromatic Light is incident on a surface separating two media.
OR
How can we convert a full-wave rectifier to a half-wave rectifier changing the connection of wires? (3)
Answer:
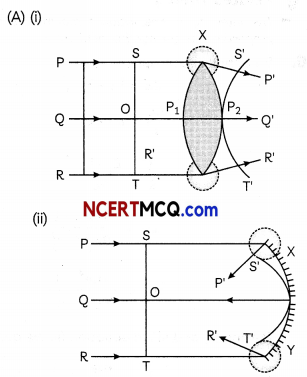
(B) The frequency and time period of an electromagnetic wave depends only on the source which produces it. The frequency is independent of the medium through which it travels. But the speed and wavelength depend on the medium through which the wave travels. Because of this, the frequency and time period of sound wave does not change due to change in the medium.
OR
If we change the connection of load resistance from point C to point B due to which no current will flow through second diode in second half cycle.
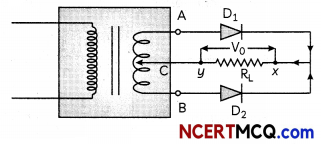
Related theory:
As the connection is altered, only one diode will be functional which Will result in decrease in efficiency
of the diode, and the output voltage will be cut down to exactly half.
![]()
Question 6.
(A) What is the significance of negative signs in the expression for the energy?
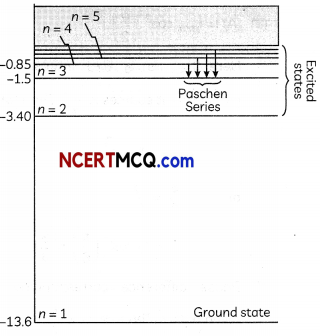
(B) Draw the energy level diagram showing how the line spectra corresponding to Paschen series occur due to transition between energy levels. (3)
Answer:
(A) Negative sign indicates that revolving electron is bound to the positive nucleus.
(B) For Paschen series, n = 3 and ni = 4, 5,..
\(\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{3^{2}}-\frac{1}{n_{i}^{2}}\right)\)
where, ni= 4, 5 ……………………..
Total energy, E (eV)
Question 7.
(A) What is the nature of the final image in a compound microscope?
(B) You are given two converging lenses of focal lengths 1.25 cm and 5 cm to design a compound microscope.
If it is desired to have a magnification of 30, find out the separation between the objective and the eyepiece? (2)
Answer:
(A) The final image in a compound microscope is inverted with respect to the object. It is
virtual and magnified.
(B) Given, fe= 5 cm;
f0= 1.25 cm
and M=-30.
Let L be the tube length (distance between the objective and the eyepiece).
∴ M = \(\frac{-L}{f_{0}}\left(1+\frac{d}{f_{e}}\right)\)
[d is a constant and equals to the normal distance of clear vision of the human eye].
Hence, -30 = \(-\frac{L}{1.25}\left(1+\frac{25}{5}\right)\)
∴ L = \(\frac{30 \times 1.25}{6}\)
= 6.25 cm
Hence, the tube [ength = 6.25 cm.
Caution
Students are often confused about the separation of objective and eyepiece. Tube Length is the separation between the objective and the eyepiece.
![]()
Question 8.
(A) How does the fringe width, in Young’s double-slit experiment change when the distance of separation between the slits and screen is doubled?
(B) In Young’s double-slit experiment maximum intensity is lo, find the intensity at a point on the screen where
(i) the phase difference between the two interfering beams is \(\frac{\pi}{3}\)
(ii) the path difference between them is \(\frac{\lambda}{4}\). (3)
Answer:
(A) Fringe width
β = \(\frac{\lambda D}{d}\)
⇒ β ∝ D
The fringe width becomes double when the distance of separation between the slits and screen is doubled.
(B) (A) I= I‘max Cos2 \(\left(\frac{\phi}{2}\right)\)
Here Imax is Io (i.e.. intensity due to independent sources is \(\frac{I_{0}}{4}\) .).
Therefore, at
Φ = \(\frac{\pi}{3}\)
or
\(\frac{\phi}{2}=\frac{\pi}{6}\)
I =I0cos2 \(\left(\frac{\pi}{6}\right)=\frac{3}{4}\) I0
(B) Phase difference corresponding to the given path difference Δx = \(\frac{\lambda}{4}\) is
Φ = \(\left(\frac{2 \pi}{\lambda}\right)\left(\frac{\lambda}{4}\right)\)
= \(\frac{\pi}{2}\) (Φ = \(\frac{2 \pi}{\lambda} \Delta x\))
\(\frac{\phi}{2}=\frac{\pi}{4}\)
I = I0 cos2\(\left(\frac{\pi}{4}\right)=\frac{I_{0}}{2}\).
Question 9.
Explain giving reasons for the following:
(A) Photoelectric current in a photocell increases with the increase in the intensity of the incident radiation.
(B) The stopping potential (V0) varies linearly with the frequency (v) of the incident radiation for a given photosensitive surface with the slope remaining the same for different surfaces.
(C) Maximum kinetic energy of the photoelectrons is independent of the intensity of incident radiation. (3)
Answer:
(A) Since number of photo electrons emitted is directly proportional to the intensity of incident radiation, therefore, as intensity increases the electron-hole pairs also increases.
(B) hv = hv0 + eV0
eV0= h(v – v0)
⇒ V0=\(\frac{h}{e}\) (v-v0)
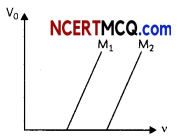
Further from graph,\(\frac{h}{e}\) slope is which is a constant and it does not depend on v.
KEmax = h(v – v0)
Hence, it depends on the frequency and not on the intensity of the incident radiation.
(C) As intensity increases, the number of photons increases but the energy remains same.
Question 10.
Derive the expression for the wavelength of lines of different spectral series in H-atom.
OR
(A) In semiconductors, thermal collisions are responsible for taking a valence electron to the conduction band. Why does the number of conduction electrons not go on increasing with time as thermal collisions continuously take place?
(B) In a p-n junction, the depletion region is 400 nm wide and an electric field of 5 x 105\(\frac{\mathrm{V}}{\mathrm{m}}\) exists in it. m
(i) What will be the height of the potential barrier?
(ii) What should be the minimum kinetic energy of a conduction electron which can diffuse from the n-side to the p-side? (3)
Answer:
10. By Bohr’s III concept
ΔE = E2 – E1
\(\frac{h c}{\lambda}\) = E2 – E1
\(\frac{1}{\lambda}=\frac{E_{2}-E_{1}}{h c}\) ……………………… (i)
E2 = – \(\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2}} \cdot \frac{1}{n_{2}^{2}}\) ………………. (ii)
E1 = – \(\frac{m e^{4}}{8 \varepsilon_{0}^{2} h^{2}} \cdot \frac{1}{n_{1}^{2}}\) ………………………. (iii)
Putting (ii) and (iii) n equation (i), we get

(A) The presence of electrons in the conduction band saturates the further production of electron-hole pairs.
(B) (i) Height of potentiaL barrier =5 x 105 V/m x 400 x 10-9
= 0.2 V
(ii) Kinetic energy
=q x V= 1.6 x 10-19 x 0.2
= 0.2 V
Question 11.
Angular width of central maxima in the Fraunhofer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength 6000 A. When the slit is illuminated by light of another wavelength, then the angular width decreases by 30%. Calculate the wavelength of this light. The same decreases in the angular width of central maximum is obtained when original apparatus is immersed in a liquid. Find the refractive index of the liquid. (3)
Answer:
An guiar width of central maximum
= \(\frac{2 \lambda}{a}\)
λ1 = 6000 Å = 60 nm,
θ1 = \(\frac{2 \lambda_{1}}{a}\)
θ2 = θ1 x 0.7
= \(\frac{2 \lambda_{1}}{a}\)
On dividing both the equations, we get
\(\frac{1}{0.7}=\frac{\lambda_{1}}{\lambda_{2}}=\frac{600}{\lambda_{2}}\)
λ2 = 420 nm
When apparatus is under liquid,

The refractive index of the given medium is 1.42.
![]()
SECTION – C
(Section C consists one case study-based question of 5 marks.)
Question 12.
A changing electric field produces a changing magnetic field and vice-versa which gives rise to a transverse wave known as electromagnetic waves. The time-varying electric field and magnetic field are mutually perpendicular to each other also perpendicular to the direction of propagation. Thus, the electromagnetic waves consist of sinusoidally time-varying electric and magnetic fields acting at right angles to each other as well as at right angles to the direction of propagation.
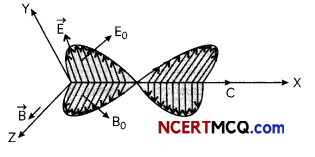
(A) The amplitudes of electric and magnetic fields in EM waves are E0 and Bo respectively.
They are related as:
(i) E0 = \(\frac{\mathrm{B}_{0}}{c}\)
(ii) E0 = cB0
(iii) cE0 = B0
(iv) E0 = c2B0
(B) Electric and magnetic field vectors in EM waves are:
(i) perpendicular to each other
(ii) parallel to each other
(iii) 270° to each other
(iv) 180° to each other
(C) A plane electromagnetic wave of frequency 25 MHz travels in free space along the x-direction. At a particular point in space and time E = 6.3 \(\hat{j} \frac{v}{m}\) the B at this point is:

(D) If E and B represent electric and magnetic field vectors of the electromagnetic waves, then the direction of propagation of the electromagnetic waves is that of:
(i) E
(ii) B
(iii) E x B
(iv) B x E
(E) In an electromagnetic wave, the electric and magnetic fields are 100 V/m and 0.265 A/m.
The maximum energy flow is:
(i) 79 \(\frac{W}{m^{2}}\)
(ii) 13.2 \(\frac{W}{m^{2}}\)
(iii) 53.0 \(\frac{W}{m^{2}}\)
(iv) 26.5 \(\frac{W}{m^{2}}\) (5)
Answer:
(A) (b) E0 = cB0
Explanation: Electric field and magnetic field vectors in an electromagnetic wave is related as \(\frac{E}{B}\) = c where c s the speed of light. The electromagnetic waves travel with the speed of Light.
(B) (a) Perpendicular to each other Explanation: The angle between electric and magnetic field vectors in EM waves is 900.
(C) (b) 2.1 x 10-8 \(\hat{k}\)T
Explanation: f’ = 25 MHz = 25 x 106 Hz,
E=6.3 \(\hat{j} \frac{v}{m}\)
E0 = 6.3
\(\left(\frac{E_{0}}{B_{0}}\right)\) = c
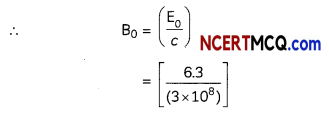
∴ E is along y-direction and wave is along x-direction hence B has to be perpendicular to both x and y axes. E x B should be along the x-direction. B shouLd be along z-direction B = B0 k
B=2.1 x 10-8\(\hat{k}\) T
(D) (c) E x B
Explanation: The electric field and the magnetic field of an electromagnetic wave are mutually perpendicular to each other and their direction of propagation is perpendicular to both the electric and magnetic fields. If E and B represent electric and magnetic field vectors of electromagnetic waves respectively, then the direction of propagation of the electromagnetic wave is along the direction of vector E x B.
![]()
Caution:
Students are often confused about the vector product of two quantities The vector product B x E gives the negative direction of the propagation of wove. The electric and magnetic fields of an electromagnetic wave are perpendicular to each other and also perpendicular to the direction of wave propagation.
Hence these are transverse waves.
(E) (d) 26.6 \(\frac{W}{m^{2}}\)
Explanation: Here, amplitude of electric field,
E0 = 100\(\frac{V}{m}\)
Amplitude of magnetic field,
B0 =0.265 \(\frac{A}{m}\)
The maximum rate of energj flow,
S = E0 x B0 = 100 x 0.265
= 26.5 \(\frac{W}{m^{2}}\).